References
- Algorithms (Sanjoy Dasgupta)
Contents
- DAG에서의 최단 경로
- Longest Increasing Subsequence (LIS; 최장 증가 부분 수열)
- Edit Distance (편집 거리)
DAG에서의 최단 경로
DAG(Directed Acyclic Graph), 즉, 유향 비순환 그래프에서의 최단 경로 알고리즘에는 다익스트라(Dijkstra) 알고리즘, 벨만-포드(Bellman-Ford) 알고리즘 등이 있습니다. 이 알고리즘을 통해서 최단 경로 문제는 쉽게 해결될 수 있다는 것을 알 수 있습니다. 이는 동적 프로그래밍의 핵심적인 부분이기 때문에, 동적 프로그래밍에 대해 시작하기 전에 한 번 요약해보도록 하겠습니다. 각 최단 경로 알고리즘에 대해서는 다른 포스팅에서 다룬 적이 있는데, 필요하시다면 참조바랍니다 !
[그래프] 다익스트라 알고리즘(Dijkstra's algorithm)
[그래프] 벨만-포드 알고리즘(Bellman-Ford Algorithm)
[그래프] 플로이드-워셜 알고리즘(Floyd-Warshall Algorithm)
DAG에서 특별히 구분되는 특징은 그래프의 노드들이 선형화(linearized)될 수 있다는 것입니다. 즉, 아래 그림처럼 모든 간선들은 왼쪽으로 오른쪽으로 가면서 한 줄로 정렬될 수 있습니다.

이를 위상 정렬(Topological Sort)이라고 하며, 이에 대해서도 아래 포스팅에서 다룬 적이 있으므로, 필요하시다면 참조 바랍니다 !
이 위상 정렬이 최단 경로를 구하는 데 도움이 되는 이유를 살펴보기 위해서, 노드 S로부터 다른 노드들까지의 거리를 계산하기를 원한다고 가정해봅시다. 구체적으로, 노드 D에 포커스를 맞추어 보겠습니다. 노드 D까지의 거리를 구하기 위한 방법은 오직 D 이전에 있는 노드 B 또는 C를 통해 가능합니다. 그래서 노드 D까지의 최단 경로를 찾기 위해서는 단지 2개의 경로를 비교하면 됩니다.
dist(D) = min{dist(B) + 1, dist(C) + 3}
이와 유사한 관계들은 모든 노드에 대해 작성될 수 있습니다. 만약 이 dist값들을 위의 그림에서 왼쪽에서부터 오른쪽의 순서로 계산한다면, 항당 노드 v에 도달할 때까지 dist(v)를 계산하는 데 필요한 모든 정보를 이미 가지고 있다고 항상 보장할 수 있습니다. 따라서 다음의 알고리즘을 통해 단일 경로에서 모든 거리를 계산하는 것이 가능합니다.

위의 알고리즘은 하위 문제(subproblems)인 {dist(u) : u \(\in\) V}의 모음들을 해결한다는 것에 주목합니다. 이 문제는 가장 작은 값을 갖는 dist(s)부터 시작하는데, 그 값은 바로 0입니다. 그런 다음 "더 큰" 하위 문제들을 진행합니다.
이는 매우 일반적인 테크닉입니다. 각 노드에서 우리는 해당 노드의 선행 노드들의 값들에 대한 함수를 사용하여 계산하는데, 여기서 이 함수는 최소합을 구하거나 최대합을 구하도록 만들 수 있습니다. 만약 최대합을 구한다면, DAG 내에서 가장 긴 경로를 얻을 수 있습니다. 또한, 합 대신에 곱셈을 사용할 수 있는데 이 경우에는 간선의 길이들의 가장 작은 곱셈 결과를 갖는 경로를 계산하게 됩니다.
동적 프로그래밍(Dynamic Programming)은 매우 강력한 알고리즘 패러다임으로, 문제 전체를 해결할 때까지 하위 문제들의 모음을 식별하고 차례로 가장 하위의 문제를 먼저 다루고, 더 큰 문제를 해결하기 위해 하위 문제들의 답을 사용합니다.
동적 프로그래밍에서는 DAG는 주어지지 않고, 내재되어 있습니다. DAG에서 노드들은 우리가 정의한 하위 문제들이고 그래프의 간선들은 하위 문제 간의 종속되어 있습니다. 만약 하위 문제 B를 해결하기 위해서 하위 문제 A에 대한 답이 필요하다면, 개념적으로 A에서 B로 향하는 간선이 있습니다. 이러한 경우에 A는 B보다 더 하위의 문제로 간주되고 명백히 항상 더 작은 문제일 것 입니다.
이제 예제들을 통해서 동적 프로그래밍에 대해 조금 더 살펴보겠습니다.
Longest Increasing Subsequence
최장 증가 부분 수열(Longest Increasing Subsequence; LIS)에서, 입력(input)은 \(a_1, \cdots, \a_n\)로 표현되는 수열(sequence of numbers)입니다. 수열은 순서를 갖는 수들의 부분집합입니다. 이때 이 수열은 \(1 \leq i_1 < i_2 < \dots < i_k \leq < n\)인 \(a_{i_1}, a_{i_2}, \dots, a_{i_k}\) 형태로 표현되고, 증가 수열(increasing subsequence)은 점점 커지는 수들의 수열 중 하나입니다. 여기서 문제는 주어진 수열에서 가장 길이가 긴 증가하는 수열을 찾는 것입니다.
예를 들어, [5 2 8 6 3 6 9 7]의 최장 증가 부분 수열은 [2 3 6 7] 입니다.

위 예제에서 화살표는 최적의 솔루션에서 연속적인 요소들 사이의 트랜지션을 표시합니다. 이 솔루션의 공간을 더 잘 이해하기 위해서, 모든 가능한 트랜지션들의 그래프를 만들어 보겠습니다. 각 요소 \(a_i\)에 대한 노드 i를 정하고, 방향을 갖는 간선들 (i, j)를 증가 부분 수열 내의 연속적인 요소가 되는 \(a_i\)와 \(a_j\)가 가능할 때마다(즉, i < j이면서 \(a_i < a_j\)일 때마다) 그래프에 추가합니다. 그래프를 그려보면 아래와 같습니다.

여기서 모든 간선 (i, j)가 i<j이기 때문에 이 그래프 G = (V, E)는 DAG입니다. 그리고, DAG내의 증가 부분 수열들과 경로들 사이에는 일대일 대응 관계에 있습니다. 따라서, 우리의 목적은 단순히 DAG에서 최장 경로를 발견하는 것과 같습니다. 알고리즘은 다음과 같습니다.
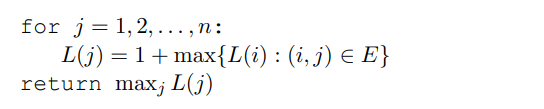
L(j)는 j에서 끝나는 최장 경로의 길이, 즉, 최장 증가 부분 수열(LIS) 입니다. 1을 더하는 이유는 간선이 아닌 노드를 카운트해야 하기 때문입니다. 위에서 최단 경로를 구하는 것과 같은 방식에 의해서 노드 j까지의 모든 경로는 j의 선행 노드들 중 하나를 지나야 하고, 따라서 이 선행 노드들 중의 최대 L(.)의 값에 1을 더합니다. 만약 j를 향하는 간선이 하나도 없다면 빈 집합에 최댓값인 0을 취합니다. 그리고 최종 답은 모든 노드가 끝에 올 수 있으므로 가장 큰 L(j)가 됩니다.
이것이 동적 프로그래밍 입니다. 원래의 문제를 해결하기 위해, 우리는 단일 경로 내에 해결될 수 있도록 하위 문제들 {L(j) : 1 \(\leq\) j \(\leq\) n}을 정의해야 합니다.
여기서 하위 문제들의 순서와 '더 작은' 하위 문제들, 즉 순서에 앞서 나타나는 하위 문제에 대한 답이 주어졌을 때 그 하위 문제를 해결하는 방법을 보여주는 관계가 있습니다. 이 경우에는, 각 하위 문제는 다음의 관계를 사용하여 해결합니다.
L(j) = 1 + max{L(i) : (i, j) \(\in\) E}
이 단계는 시간이 얼마나 걸릴까요? 이는 j의 선행 노드들을 요구합니다. 이를 위해서는 역그래프 \(G^R\)의 인접 리스트(선행 시간에 구축가능)가 유용합니다. 그런 다음 L(j)의 계산은 j의 차수에 비례하는 시간이 걸리므로 \(|E|\)에 대해 linear한 시간이 걸립니다.
이는 최대 \(O(n^2)\)이며, 입력 배열이 오름차순으로 정렬될 때 최대가 됩니다.
여기서는 단지 최장 증가 부분 수열의 길이만을 구하는데, 만약 이 수열의 원소들을 찾고자 한다면 L(j)를 계산하는 동안, j까지 최장 경로상의 끝 바로 전 노드 prev(j)를 저장하여 구할 수 있습니다. 따라서 정답을 다 구한 후, 끝 노드에서 되돌아가면서 수열의 각 노드들을 거꾸로 찾아가 최장 증가 부분 수열의 원소들을 구할 수 있습니다.
최장 증가 부분 수열의 길이와 그 경로를 모두 구하는 문제를 C++로 구현하면, 다음과 같이 구현할 수 있습니다. 위의 설명과는 조금 다르게, DAG를 구성하지 않고 배열을 모두 탐색하는 것으로 해결하였습니다. 둘 다 동일한 시간복잡도를 갖습니다.
#include <iostream>
#include <vector>
#include <algorithm>
void LIS1(const std::vector<int>& seq)
{
const int N = seq.size();
std::cout << "Seq : ";
for (int i = 0; i < N; i++) {
std::cout << seq[i] << " ";
}
std::cout << "\n";
std::vector<int> dp(N, 0);
std::vector<int> prev(N, -1);
dp[0] = 1;
for (int i = 1; i < N; i++) {
int val = 0;
for (int j = 0; j < i; j++) {
if (seq[j] < seq[i]) {
if (dp[j] > val) {
val = dp[j];
prev[i] = j;
}
}
}
dp[i] = val + 1;
}
int max_path = 0;
int end_node = 0;
for (int i = 0; i < N; i++) {
if (max_path < dp[i]) {
max_path = dp[i];
end_node = i;
}
}
std::vector<int> path;
while (end_node != -1) {
path.push_back(end_node);
end_node = prev[end_node];
}
reverse(path.begin(), path.end());
std::cout << "\nLength : " << max_path << "\n";
std::cout << "Path : ";
for (int node : path) {
std::cout << node << " ";
}
std::cout << "\n\n";
}
int main(int argc, char* argv[])
{
std::vector<int> seq{ 5, 2, 8, 6, 3, 6, 9, 7 };
LIS1(seq);
}
O(n\(\log n\))의 시간복잡도를 갖는 솔루션
위의 알고리즘은 배열의 원소를 하나씩 탐색하면서, 그 이전의 원소들을 모두 탐색하기 때문에 O(\(n^2\))의 시간복잡도를 갖습니다. 따라서 수열의 원소 수가 많으면 시간이 너무 오래 걸리게 됩니다.
이보다 조금 더 빠르게 해결할 수 있는 알고리즘이 있는데, 이 알고리즘은 배열의 원소를 하나씩 탐색하면서, 그 이전의 원소를 모두 탐색하는 것이 아닌 이진 탐색(binary search)를 통해 해당 원소가 들어가는 위치를 찾아서 LIS를 찾게 됩니다. 이 알고리즘의 key point는 LIS를 찾는 과정에서 현재 원소가 이때까지 찾은 LIS의 마지막 원소보다 작은 경우, LIS에 들어갈 위치를 이진 탐색으로 찾은 후, 원래 LIS에 있던 원소를 대체하게 됩니다.
여기서 각 원소에서 이진 탐색의 시간이 O(\(\log n\))이 걸리므로, 최종 시간 복잡도는 O(\(n\log n\))이 됩니다.
C++로 구현 시, 이진 탐색을 통해 원소의 위치를 찾는 것은 직접 구현해도 되지만 <algorithm> 헤더의 lower_bound 함수를 사용할 수 있습니다.
#include <iostream>
#include <vector>
#include <algorithm>
void LIS2(const std::vector<int>& seq)
{
const int N = seq.size();
std::cout << "Seq : ";
for (int i = 0; i < N; i++) {
std::cout << seq[i] << " ";
}
std::cout << "\n";
std::vector<int> lis;
std::vector<int> path_len(N, -1);
lis.push_back(seq[0]);
path_len[0] = 0;
int max_path = 1;
for (int i = 1; i < N; i++) {
if (lis.back() < seq[i]) {
path_len[i] = max_path;
lis.push_back(seq[i]);
max_path += 1;
}
else {
int idx = std::lower_bound(lis.begin(), lis.end(), seq[i]) - lis.begin();
path_len[i] = idx;
lis[idx] = seq[i];
}
}
std::cout << "\nLength : " << max_path << "\n";
std::vector<int> path;
for (int i = N - 1; i >= 0; i--) {
if (max_path == path_len[i] + 1) {
path.push_back(i);
max_path--;
}
}
reverse(path.begin(), path.end());
std::cout << "Path : ";
for (int node : path) {
std::cout << node << " ";
}
std::cout << "\n\n";
}
int main(int argc, char* argv[])
{
std::vector<int> seq{ 5, 2, 8, 6, 3, 6, 9, 7 };
LIS2(seq);
}
위의 코드들은 참고하면 아래의 백준 문제들을 해결할 수 있습니다 !
(정답과 매칭하기 위해 약간의 코드 수정은 필요합니다)
- 11722번. 가장 긴 증가하는 부분 수열
- 12015번. 가장 긴 증가하는 부분 수열 2
- 12738번. 가장 긴 증가하는 부분 수열 3
- 14002번. 가장 긴 증가하는 부분 수열 4
- 14003번. 가장 긴 증가하는 부분 수열 5
Edit Distance
맞춤법 검사기는 맞춤법이 잘못된 가능성이 있는 단어를 만났을 때, 사전에서 가까운 다른 단어를 찾습니다. 이 경우 가깝다는 것을 어떻게 적절하게 판단할까요?
두 문자열 간의 거리의 대한 자연스러운 척도는 이 문자열이 정렬되거나 일치될 수 있는 정도가 될 수 있습니다. 기술적으로 정렬은 단순히 문자열 위에 다른 단어의 문자열을 쓰는 방법입니다. 예를 들어, SNOWY와 SUNNY라는 단어의 두 가지 가능한 정렬 방법은 다음과 같습니다.
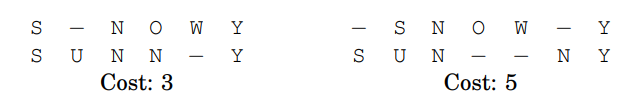
문자 '-'는 gap을 나타냅니다. 즉, 여기에는 얼마든지 다른 문자열이 놓일 수 있습니다. 정렬에 대한 cost는 문자들이 다른 컬럼(columns)의 수 입니다. 그리고 두 문자열들 간의 편집 거리(edit distance)는 가장 최적의 정렬의 cost가 됩니다. 여기서 SNOWY와 SUNNY는 3의 cost가 필요한 정렬보다 더 좋은 정렬이 없다는 것을 알 수 있습니다.
편집 거리는 첫 번째 문자열을 두 번째 문자열로 변경하는데 필요한 최소한의 편집(edit: 삽입, 삭제, 대체) 횟수로 생각할 수 있기 때문에 이와 같은 이름이 붙었습니다. 예를 들어, SNOWY에서 SUNNY로의 변환은 U 삽입, O->N 대체, W 삭제, 3번의 편집이 필요합니다.
일반적으로 두 문자열들 사이에는 가능한 배치 방법이 많이 존재합니다. 그러나 가장 좋은 배치 방법을 찾기 위해 모든 배치를 찾아보는 것은 몹시 비효율적이기 때문에 여기서 동적 프로그래밍 기법이 필요합니다.
DP Solution
DP를 사용하여 문제를 해결할 때, 가장 먼저 알아봐야 하는 것은 바로 '하위 문제가 무엇인가?'라는 것입니다.
이 문제의 목적은 두 개의 문자열들 x[\(1, \cdots, m\)]과 y[\(1, \cdots, n\)] 사이의 편집 거리를 발견하는 것입니다. 여기서 괜찮은 하위 문제는 무엇일까요? 당연히 전체 문제를 해결하는 방법을 일부로 나누는 것 입니다. 그러면, 첫 번째 문자열의 일부 접두사 x[\(1, \cdots, i\)]와 두 번째 문자열의 일부 접두사 y[\(1, \cdots, j\)] 사이의 편집 거리를 살펴보는 것은 어떨까요? 여기서 이 하위 문제들을 E(i, j)라고 부르도록 하겠습니다. 그렇다면 최종 목적은 E(m, n)을 계산하는 것이 됩니다.

이 방법을 사용하기 위해서, E(i, j)를 더 작은 하위 문제로 표현해야 합니다.
x[\(1, \cdots, i\)]와 y[\(1, \cdots, j\)] 사이에서 최고의 정렬을 찾기 위해서 어떻게 해야 할까요? 분명한 것은 두 문자열들의 가장 오른쪽 컬럼(문자)은 아래의 3 가지 중의 하나가 된다는 것입니다.

첫 번째 케이스는 이 컬럼에 대해 1의 cost가 발생하고, x[\(1, \cdots, i-1\)]와 y[\(1, \cdots, j\)]와 정렬하는 것이 남게 됩니다. 그러나 이는 정확하게 E(i-1, j)라는 하위 문제입니다. 두 번째 케이스의 경우 또한 1의 cost가 발생합니다. 여기서도 x[\(1, \cdots, i\)]와 y[\(1, \cdots, j-1\)]를 정렬해야 합니다. 이는 또 다른 하위 문제 E(i, j-1)이 됩니다. 그리고 마지막의 경우에서는 x[i]와 x[j]가 같지 않다면 cost 1이 발생하고, 만약 같다면 0이 되어 남은 하위 문제는 E(i-1, j-1)이 됩니다.
정리하면 E(i, j)는 3개의 더 작은 하위 문제인 E(i-1, j), E(i, j-1), E(i-1,j-1)로 표현되었습니다. 하지만 이들 중 어느 것이 정답인지 알 수 없기 때문에 이 하위 문제를 모두 시도하여 가장 좋은 것을 선택해야 합니다.

예를 들어, EXPONENTIAL과 POLYNOMIAL 사이의 편집 거리를 계산할 때, 하위 문제 E(4, 3)은 접두사 EXPO와 POL에 해당합니다. 그리고, 이들 중 가장 좋은 정렬의 오른쪽 컬럼은 다음 중의 하나이어야 합니다.
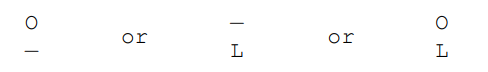
따라서, E(4, 3) = min{1 + E(3, 3), 1 + E(4, 2), 1 + E(3, 2)} 입니다.
모든 하위 문제 E(i, j)에 대한 정답은 아래의 2차원 테이블을 형성합니다.

이 하위 문제들은 어떠한 순서로 풀어야 할까요? 여기서는 E(i, j)가 계산되기 전에 E(i-1, j), E(i, j-1), E(i-1, j-1)이 처리되는 한 어떠한 순서도 상관없습니다. 예를 들어, 표를 한 번에 한 행씩, top에서 bottom 행 방향으로 왼쪽에서 오른족으로 이동할 수 있습니다. 또는 열 별로 채워나갈 수도 있습니다.
이제 하위 문제들과 그 순서를 모두 지정하였습니다. 이제 단지 DP 의 'base cases'만 남아 있습니다. 현재 상황에서 E(0, .)과 E(., 0)은 쉽게 계산할 수 있습니다. E(0, j)는 길이가 0인 x의 접두사, 즉, 빈 문자열과 y의 처음 j개의 문자 사이의 편집 거리이며, 이들 값은 명확히 j가 됩니다. 유사하게 E(i, 0) = i가 됩니다.
따라서, 편집 거리 알고리즘을 의사 코드로 작성하면 다음과 같이 작성할 수 있습니다.

이 프로시저는 위의 하위 문제 테이블을 각 행에서 왼쪽에서 오른쪽으로, 그리고 행에서 행으로 채웁니다. 각 항목은 채우는 데 상수 시간이 걸리기 때문에, 전체 실행 시간의 표의 크기와 같습니다. 즉, O(mn)이 됩니다.
그리고 위의 예제 EXPONENTIAL과 POLYNOMIAL에서 편집 거리는 6이 됩니다.
The underlying dag
모든 동적 프로그램은 기본적으로 DAG 구조를 갖습니다. 즉, 각 노드를 하위 문제를 나타내는 것으로 생각하고, 각 간선을 하위 문제를 처리할 수 있는 순서에 대한 제약으로 생각합니다. v를 가리키는 노드들 \(u_1, \cdots, u_k\)을 가진다는 것은 하위 문제 v는 \(u_1, \cdots, u_k\)에 대한 답을 알자마자 해결될 수 있습니다.
위의 편집 거리에서, DAG의 노드들은 테이블에서 하위 문제에 대응되거나 (i, j) 위치에 해당합니다. DAG의 간선은 아래 그림에서 보듯 (i-1, j) -> (i, j), (i, j-1) -> (i, j), 그리고 (i-1, j-1) -> (i, j) 형식의 선행 조건 제약입니다.

사실, 조금 더 나아가 간선에 가중치를 추가하여 편집 거리가 DAG의 최단 경로로 주어지도록 할 수 있습니다. 이를 확인하려면 {(i-1, j-1) -> (i,j) : x[i] = y[i]} (위 그림에서 점선으로 표시)를 제외한 모든 간선의 길이를 1로 설정합니다 (나머지는 0). 그럼 최종 답은 단순히 노드 s = (0, 0)과 t = (m, n) 간의 거리가 됩니다. 따라서 위 그림처럼 가능한 최단 경로 중 하나가 표시되게 됩니다. 이 경로상에서 아래로의 이동은 삭제, 오른쪽으로 이동은 추가, 대각선 이동은 일치이거나 대체가 됩니다.
Edit Distance를 C++로 구현하면 다음과 같습니다.
#include <iostream>
#include <vector>
#include <algorithm>
#include <string>
int edit_distance(std::string_view str1, std::string_view str2)
{
const int m = str1.length();
const int n = str2.length();
std::vector<std::vector<int>> tb(m + 1, std::vector<int>(n + 1, 0));
for (int i = 0; i <= m; i++)
tb[i][0] = i;
for (int j = 1; j <= n; j++)
tb[0][j] = j;
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
tb[i][j] = std::min(tb[i - 1][j - 1] + ((str1[i - 1] == str2[j - 1]) ? 0 : 1), std::min(tb[i - 1][j] + 1, tb[i][j - 1] + 1));
}
}
return tb[m][n];
}
int main(int argc, char* argv[])
{
std::string str1 = "EXPONENTIAL";
std::string str2 = "POLYNOMIAL";
edit_distance(str1, str2);
}
여기서 O(mn)의 공간복잡도를 갖는데, 사실 한 행의 DP 결과는 이전 행의 정보만 있다면 계산 가능합니다. 따라서, 다음과 같이 O(2n)의 공간복잡도로 최종 편집 거리를 계산할 수 있습니다.
#include <iostream>
#include <vector>
#include <algorithm>
#include <string>
int edit_distance(std::string_view str1, std::string_view str2)
{
const int m = str1.length();
const int n = str2.length();
std::vector<std::vector<int>> tb(2, std::vector<int>(n + 1, 0));
for (int i = 0; i <= n; i++)
tb[0][i] = i;
for (int i = 1; i <= m; i++) {
int idx = i % 2;
tb[idx][0] = i;
for (int j = 1; j <= n; j++) {
if (str1[i - 1] == str2[j - 1]) {
tb[idx][j] = tb[1 - idx][j - 1];
paths[j - 1] = 0;
}
else {
tb[idx][j] = std::min(tb[1 - idx][j - 1], std::min(tb[1 - idx][j], tb[idx][j - 1])) + 1;
}
}
}
return tb[m % 2][n];
}
int main(int argc, char* argv[])
{
std::string str1 = "EXPONENTIAL";
std::string str2 = "POLYNOMIAL";
edit_distance(str1, str2);
}
백준에 편집거리에 대한 문제가 2개 있습니다.
https://www.acmicpc.net/problem/7620
7620번: 편집 거리
가장 짧은 편집 스크립트를 출력한다. 한 명령을 한 줄에 하나씩 출력하며, 문제의 괄호에 나와있는 (a, d, m, c)중 하나를 출력하고, 그 명령을 수행하는데 사용한 글자를 출력한다. (출력할 글자
www.acmicpc.net
https://www.acmicpc.net/problem/17161
17161번: 편집 거리 (Hard)
가장 짧은 편집 스크립트를 출력한다. 한 명령을 한 줄에 하나씩 출력하며, 문제의 괄호에 나와있는 (a, d, m, c)중 하나를 출력하고, 그 명령을 수행하는데 사용한 글자를 출력한다. (출력할 글자
www.acmicpc.net
둘 다 동일한 문제이긴 한데, 17161번의 경우에는 메모리 제한이 16MB으로 아마 O(max(m, n))의 공간복잡도로 해결해야 하는 것 같습니다. 그래서, DP 기법을 이용하지만 메모리를 더 적게 사용하는 다른 알고리즘(ex, Hirschberg 알고리즘)을 사용해야 하는 것으로 추측됩니다.
7620번의 경우에는 위에서 설명한 방법으로 해결할 수는 있지만 메모리 제한이 128MB으로 O(mn)이 아닌 O(2n)의 공간복잡도를 사용하는 DP를 적용해야 합니다. 다만, 문제에서 편집 커맨드를 찾아야 합니다. 즉, 최소의 편집 거리를 갖는 경로를 찾아야 하는데, 경로는 위에서 설명한 O(2n)의 공간복잡도로는 해결할 수 없습니다. 다른 알고리즘이 아닌 이번 포스팅에서 배웠던 내용으로 해결할 수는 없을까하여 검색해보니 방법은 존재 했습니다(link 참조). 편집 거리에서 이동 가능한 방향은 right(추가)/down(삭제)/right-down(일치)/right-down(대체) 이기 때문에 비트 표기로 2비트의 공간만 사용하여 경로를 기록할 수 있습니다. 따라서, 4개의 하위 문제에 대한 경로를 8비트에 담도록 최적화하여 메모리 공간을 절약할 수 있습니다.
#include <iostream>
#include <vector>
#include <algorithm>
#include <string>
struct Path {
// 0 : down(del)
// 1 : right(ins)
// 2 : down-right(rep)
// 3 : down-right(copy)
uint8_t lt : 2;
uint8_t lb : 2;
uint8_t rt : 2;
uint8_t rb : 2;
};
std::vector<std::vector<int>> tb;
std::vector<std::vector<Path>> paths;
void set_path(int m, int n, uint8_t dir)
{
int i = m / 2;
int j = n / 2;
if (m % 2 && n % 2)
paths[i][j].rb = dir;
else if (m % 2)
paths[i][j].lb = dir;
else if (n % 2)
paths[i][j].rt = dir;
else
paths[i][j].lt = dir;
}
int get_path(int m, int n)
{
int i = m / 2;
int j = n / 2;
if (m % 2 && n % 2)
return paths[i][j].rb;
else if (m % 2)
return paths[i][j].lb;
else if (n % 2)
return paths[i][j].rt;
else
return paths[i][j].lt;
}
int edit_distance(std::string_view str1, std::string_view str2)
{
const int m = str1.length();
const int n = str2.length();
tb.resize(2, std::vector<int>(n + 1, 0));
paths.resize((m / 2) + 10, std::vector<Path>((n / 2) + 10));
for (int i = 0; i <= n; i++) {
tb[0][i] = i;
}
for (int i = 0; i < paths.size(); i++) {
set_path(0, i, 1);
}
for (int i = 0; i < paths[0].size(); i++) {
set_path(i, 0, 0);
}
for (int i = 1; i <= m; i++) {
int idx = i % 2;
tb[idx][0] = i;
for (int j = 1; j <= n; j++) {
if (str1[i - 1] == str2[j - 1]) {
tb[idx][j] = tb[1 - idx][j - 1];
set_path(i, j, 3);
}
else {
tb[idx][j] = std::min(tb[1 - idx][j - 1], std::min(tb[1 - idx][j], tb[idx][j - 1])) + 1;
if (tb[idx][j] == tb[1 - idx][j] + 1) {
set_path(i, j, 0);
}
else if (tb[idx][j] == tb[idx][j - 1] + 1) {
set_path(i, j, 1);
}
else {
set_path(i, j, 2);
}
}
}
}
std::vector<std::pair<char, char>> results;
int i_idx = m;
int j_idx = n;
while (i_idx != 0 || j_idx != 0) {
int dir = get_path(i_idx, j_idx);
if (dir == 0) { // down(del)
results.push_back({ 'd', str1[i_idx - 1] });
i_idx--;
}
else if (dir == 1) { // right(ins)
results.push_back({ 'a', str2[j_idx - 1] });
j_idx--;
}
else if (dir == 2) { // down-right(rep)
results.push_back({ 'm', str2[j_idx - 1] });
i_idx--; j_idx--;
}
else { // down-right(copy)
results.push_back({ 'c', str1[i_idx - 1] });
i_idx--; j_idx--;
}
}
reverse(results.begin(), results.end());
for (int i = 0; i < results.size(); i++) {
printf("%c %c\n", results[i].first, results[i].second);
}
return tb[m % 2][n];
}
int main(int argc, char* argv[])
{
std::string str1 = "EXPONENTIAL";
std::string str2 = "POLYNOMIAL";
//std::cin >> str1;
//std::cin >> str2;
edit_distance(str1, str2);
}
'Data Structure & Algorithm > 알고리즘' 카테고리의 다른 글
| [DP] 외판원 문제 (Traverling Salseman Problem) (0) | 2022.04.15 |
|---|---|
| [DP] Knapsack Problem (0-1 Knapsack) (0) | 2022.04.14 |
| 최소 신장 트리 (Minimum Spanning Tree) (0) | 2022.04.11 |
| 피보나치 수열 (0) | 2021.10.26 |
| 보이어-무어-호스풀 알고리즘(Boyer-Moore-Horspool Algorithm) (0) | 2021.10.12 |




댓글