References
- Algorithms (Sanjoy Dasgupta)
Contents
- Minimum Spanning Tree
- 크루스칼 알고리즘 (Kruskal's algorithm)
- Union-Find 자료구조
- C++ 구현
그리디(Greedy) 알고리즘들은 가장 명백하게 당장의 이득을 제공하는 다음 조각을 항상 선택하면서 한 조각씩 해결책을 만들어 나갑니다. 이와 같은 접근 방법이 계산을 요구하는 작업에 많은 피해를 줄 수 있을지라도, 최적이 되는 해결책을 얻을 수도 있습니다. 그리디 알고리즘의 예로 이번 포스팅에서는 최소 신장 트리(Minimum Spanning Tree; MST)에 대해 알아보고자 합니다.
최소 신장 트리
컴퓨터들을 쌍으로 연결함(linking)으로써 네트워크를 구성한다고 가정해봅시다. 이는 노드(nodes)들이 컴퓨터이고 무향 간선(undirected edges)들이 링크들인 그래프 문제로 바꿀 수 있습니다. 그리고 목표는 노드들을 연결할 수 있는 충분한 간선들을 선택하는 것입니다. 다만, 이것이 전부가 아니라 각 링크는 유지보수 비용을 가지는데, 이는 간선들의 가중치로 반영됩니다. 예를 들어, 아래의 이미지에서 가장 비용이 적게 드는 네트워크는 어떤 것일까요?

일단 직관적으로 정답은 사이클을 포함하지 않는 간선들의 집합이라는 것이라는 것을 알 수 있습니다. 이는 사이클로부터 간선을 제거하는 것은 연결성(connectivity)를 손상시키지 않으면서 비용을 줄일 수 있기 때문입니다.
Property 1: 사이클의 간선 제거는 그래프를 disconnect시킬 수 없다.
따라서, 해결책은 연결되면서 비사이클(acyclic)이어야 합니다. 이와 같은 종류의 무향 그래프(undirected graph)들을 트리(tree)라고 부릅니다. 여기서 우리가 원하는 특정 트리는 최소한의 total 가중치를 갖는 최소 신장 트리입니다.
우선 최소 신장 트리의 공식적인 정의를 살펴보겠습니다.
- Input: 무향 그래프(undirected graph) G = (V, E); 간선의 가중치 \(w_e\).
- Output: 트리(tree) T = (V, E'), 여기서 E'는 E의 부분집합이다. 그리고 다음을 최소화한다.
\[\text{weight}(T) = \sum_{e \in E'} w_e\]
위에서 본 예제 이미지에서, 최소 신장 트리는 16의 비용을 갖습니다.
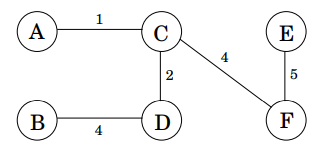
하지만, 이것이 유일한 최적의 답은 아닙니다.
잠깐 트리에 대해 언급하자면, 트리는 연결되어 있고 비순환적(acyclic)인 무향(undirected) 그래프입니다. 트리를 유용하게 만드는 것 중의 대부분은 트리 구조의 단순성인데, 예를 들면 다음과 같습니다.
Property 2: n개의 노드를 가진 트리는 n-1개의 간선을 갖는다.
이는 빈 그래프에서 시작해서 한 번에 하나의 간선으로 트리를 형성함으로써 확인할 수 있습니다. 초기에는 n개의 노드들이 각각 서로 연결되지 않고, 자기 자신과 연결된 컴포넌트(component)입니다. 간선이 추가됨으로써 이 컴포넌트들은 병합됩니다. 각 간선은 두 개의 다른 컴포넌트들을 합치기 때문에 트리가 완전히 형성될 때 정확히 n-1개의 간선이 추가됩니다.
조금 더 자세히 설명하면, 특정 간선 {u, v}가 선택되었을 때, u와 v는 분리된 컴포넌트들에 위치하고 있다는 것을 확신할 수 있습니다. 그렇지 않으면, 두 컴포넌트 사이의 경로가 이미 존재하고 이 간선은 사이클을 만들게 됩니다. 간선을 추가하면 이들 두 컴포넌트들은 병합되고, 그 때문에 간선에 의해서 연결된 컴포넌트의 총 수는 감소하게 됩니다. 이 과정에서 컴포넌트의 갯수는 n개에서 1개로 감소합니다.
반대 또한 성립합니다.
Property 3: 임의로 연결된 무향 그래프 G = (V, E)가 \(|E| = |V| -1\)이 성립한다면 트리이다.
이 특성을 증명하기 위해서는 그래프 G가 사이클이 아니라는 것을 보일 필요가 있습니다. 이 방법은 다음의 반복적인 프로세스를 수행하는 것입니다: 그래프가 사이클을 포함하는 동안, 이 사이클로부터 하나의 간선을 제거합니다. 이 과정을 통해 사이클이 없으면서 연결된 그래프 G' = (V, E'), \(E' \in E\)인 그래프를 만들고 종료됩니다. 그리하여 G'는 트리가 되고 그 결과 Property 2에 의해서 \(|E'| = |V| - 1\)이 됩니다. 따라서, E' = E인, 즉, 제거된 간선이 없는 그래프 G는 비순환 그래프가 됩니다.
정리하면, 연결 그래프는 간선의 수를 세어서 트리인지 아닌지 구별할 수 있습니다. 여기서 다른 성질을 살펴보겠습니다.
Property 4: 무향 그래프가 트리라면 임의의 노드들의 쌍 사이에 유일한 경로를 가진다
트리에서 임의의 두 노드들은 그들 사이에 하나의 경로만을 가집니다. 만약 두 개의 경로를 가진다면 이들 경로들의 결합은 사이클을 포함합니다.
다시 말해, 만약 그래프가 어떤 두 노드들 사이에 경로를 가진다면, 그때 노드들은 연결되어 있습니다. 만약 이들 경로가 유일하다면, 이 그래프는 비순환적입니다 (사이클은 임의의 노드들의 쌍 사이에 두 개의 경로를 가지기 때문).
크루스칼 알고리즘
크루스칼의 MST 알고리즘은 빈 그래프로 출발하여 다음의 규칙에 의하여 E로부터 간선을 선택합니다.
반복적으로 사이클을 만들지 않는 가장 작은 가중치를 갖는 다음 간선을 추가한다.
즉, 사이클을 만드는 간선들을 고려하면서, 단순하게 당장에 가장 가중치가 적은 간선을 선택합니다. 이것이 바로 그리디 알고리즘입니다. 즉, MST를 만드는 모든 선택은 가장 명백하게 당장의 이득을 가지는 간선이 됩니다.
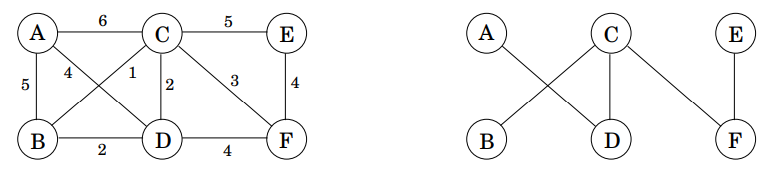
위의 이미지를 예시로 살펴보겠습니다.
왼쪽 그래프에서 우리는 총 10개의 간선을 확인할 수 있고, 가중치 순으로 나열하면 다음과 같습니다.
B-C, C-D, B-D, C-F, D-F, E-F, A-D, A-B, C-E, A-C
빈 그래프에 위에 나열한 순서대로 간선을 추가하면, 처음 두 개(B-C, C-D)까지는 성공이지만 세 번째 B-D가 추가되면 사이클이 형성됩니다. 따라서 B-D는 무시하고 다음으로 이동합니다. 이렇게 마지막까지 진행하면 최종 결과는 가장 작은 비용 14를 가진 오른쪽 그래프가 됩니다.
크루스칼 알고리즘의 정확성(correctness)는 cut-property를 따릅니다. cut-property는 다른 MST 알고리즘들을 정당화하기 충분한 특성입니다.
Cut Property
MST를 구축하는 과정에서 말했듯이, 이미 많은 간선들을 선택했고 여기까지는 올바른 과정 위에 있습니다. 그렇다면 다음에 추가될 간선은 어떤 것일까요? 다음의 보조 정리(lemma)는 이 선택에 있어서 많은 유연성을 제공합니다.
Cut-Property
간선들 X는 그래프 G = (V, E)의 MST의 부분이다. S와 V-S 사이를 가로지르지 않는 X를 위한 노드들의 부분집합 S를 pick한다. 그리고 e가 이 분할(partition)을 가로지르는 가장 작은 값을 갖는 간선이라고 하자. 그때, \(X\cup \{e\}\)는 어떤 MST의 부분이 된다.
여기서 cut은 S와 V-S의 두 그룹으로 나누어진 정점들의 임의의 파티션(partition)입니다. 이 특성이 말하는 것은 임의의 cut을 가로지르는(즉, S 내의 정점과 V-S 내의 정점 사이) 가장 작은 값을 갖는 간선을 더하는 것은 항상 안전하고, 제공된 X가 cut을 가로지르는 어떠한 간선도 갖지 않는다 라는 것입니다.
왜 그런가 하면, 간선들인 X는 어떤 MST T의 부분(part)입니다. 만약 새로운 간선 e가 T의 부분이 되면, 그때는 아무것도 증명되지 않습니다. 따라서, e가 T 내에 없다고 가정합니다. T의 간선들 중 하나만 변경하여 T를 대체함으로써 \(X \cup \{e\}\)를 포함하는 다른 MST T'를 구성할 수 있습니다.

T에 간선 e를 추가해봅시다. T가 연결되어 있기 때문에, e의 끝점들 사이에 이미 경로를 가지고 있고 따라서 e를 추가하는 것은 사이클을 만듭니다. 이 사이클은 cut(S, V-S)를 가로지르는 다른 간선 e'도 가지고 있어야 합니다(위의 그림 참조). 만약 이 간선이 제거된다면, \(T' = T \cup \{e\} - \{e'\}\)가 남게 되고, 트리가 됩니다. T'는 e'가 사이클 간선이기 때문에 위에서 본 Property 1에 의해 연결되었습니다. 그리고 T와 동일한 간선의 수를 갖습니다. 그래서 Property 2와 3에 의해서, 트리가 됩니다.
게다가, T'는 최소 신장 트리가 됩니다. T'와 T의 가중치를 비교하면 다음과 같습니다.
\[\text{weight}(T') = \text{weight}(T) + w(e) - w(e')\]
e와 e'는 모두 S와 V-S 사이를 교차하며, e는 특히 가장 가벼운 간선입니다. 따라서 \(w(e) \leq w(e')\)이면서, \(\text{weight}(T') \leq \text{weight}(T)\) 입니다. T가 MST이기 때문에 \(\text{weight}(T') = \text{weight}(T)\)가 되어야 하고, T'도 MST가 되어야 합니다.
아래 이미지는 cut property의 예를 보여줍니다. 여기서 어떤 간선이 e' 일까요?

그림 (a)는 무향 그래프라는 것을 보여줍니다.
그림 (b)의 왼쪽 이미지에서 집합 X는 3개의 간선을 갖습니다. 그리고 오른쪽 이미지는 MST T의 부분입니다.
그림 (c)에서, 만약 S = {A, B, C, D}이라면, 그때 cut(S, V-S)를 가로지르는 최소 가중치 간선 중의 하나는 e = {D, E} 입니다. \(X \cup \{e\}\)는 그림 (c)의 오른쪽 이미지에서 있는 MST T'의 부분입니다.
의사코드
위에서 설명한 내용들을 통해 크루스칼 알고리즘(Kruskal's algorithm)의 정확성(correctness)를 증명할 수 있습니다. 어떤 순간에, 이미 선택된 간선들은 트리 구조를 갖는 각각의 연결된 컴포넌트들의 컬렉션으로 부분적인 솔루션을 형성합니다. 추가될 다음 간선 e는 이들 컴포넌트 두 개를 연결합니다. 여기서 두 컴포넌트는 \(T_1\)과 \(T_2\)라고 부르겠습니다. e가 사이클을 만들지 않는 가장 작은 간선이기 때문에 \(T_1\)과 \(V-T_1\) 사이의 가장 작은 간선이 될 수 있고 그리하여 cut property를 만족합니다.
크루스칼 알고리즘의 자세한 구현은 다음과 같습니다.
각 스테이지에서 알고리즘은 현재 부분 솔루션에 추가될 간선을 선택합니다.
이를 위해서 후보가 되는 간선 u - v를 검사할 필요가 있습니다. 후보가 되는 간선은 끝점들 u와 v가 다른 컴포넌에 놓이는지를 보는데, 다시 말해 간선이 사이클을 만드는지를 테스트합니다. 그리고 이 테스트를 통과하는 즉시, 이 후보 간선은 선택되고 이와 상응하는 컴포넌트들은 합쳐집니다.
이 테스트는 union-find를 통해서 수행할 수 있습니다.
union-find 자료구조의 연산은 아래와 같이 3개가 있습니다. 이에 대한 자세한 내용은 아래에서 다루도록 하고, 지금은 간단히 어떠한 연산들이 있는지만 살펴보겠습니다.
- makeset(x) : x만을 포함하는 singleton set을 만듭니다. 즉, 알고리즘 초기에 이 연산을 통해서 각 노드는 스스로가 컴포넌트가 됩니다.
- find(x) : x가 어떤 집합에 속하는지 찾습니다. 알고리즘에서 노드들의 쌍이 동일한 집합에 속하는지 반복적으로 검사할 때 이 연산을 수행합니다.
- union(x, y) : x와 y가 포함된 집합들을 병합(merge)합니다. 알고리즘에서 사이클을 형성하지 않는 노드를 선택하여 추가할 때마다 이 연산을 통해서 컴포넌트들을 병합합니다.
union-find 자료구조를 사용한 최종 알고리즘은 다음과 같습니다.

여기서 makeset은 \(|V|\)번 수행되고, find는 \(2|E|\)번, 그리고 union은 \(|V|-1\)번 수행됩니다.
Disjoint 집합을 위한 자료구조 (union-find)
Disjoint 집합을 저장하기 위한 방법 중 하나는 아래 그림의 유향(directed) 트리처럼 저장하는 것입니다.

트리의 노드들은 집합의 요소가 되고, 순서없이 정렬됩니다. 그리고 각 노드는 트리의 루트로 향하는 포인터들을 가집니다. 이 루트 요소는 집합을 표현하기 위한 단순한 대표(representative) 또는 이름(name)이 됩니다. 이 요소들은 부모 노드를 가리키는 포인터가 자기 자신을 가리키며, 다른 요소들과 구별됩니다.
이렇게 부모 포인터 \(\pi\)를 추가하기 위해, 각 노드는 랭크(rank)를 가지는데, 이 랭크는 그 노드로부터 달려있는 서브 트리의 높이(height 또는 level)로 해석됩니다.

의사코드를 살펴보면 알 수 있듯이, 각 노드들을 하나의 컴포넌트로 초기화하는 makeset 연산은 상수 시간 연산자입니다. 이에 반해, find 연산은 트리의 루트로 부모 포인터를 따라가기 때문에 트리 높이에 비례하는 시간이 걸립니다. 따라서 트리를 구축하는 과정에서 최대한 트리를 얕게 만들도록 노력해주어야 합니다.
두 집합을 병합하는 것은 쉽습니다. 즉, 한 포인터의 루트를 다른 포인터의 루트로 만들면 됩니다. 그러나 여기서 선택해야 할 것이 있습니다. 만약 집합의 루트들(대표들)이 \(r_x\)와 \(r_y\)라면, 어떤 것을 대표로 해야 할까요? 트리의 높이는 계산 효율의 걸림돌이 될 수 있기 때문에, 효율을 높일 수 있는 전략은 짧은 트리의 루트가 긴 트리의 루트를 가리키도록 만드는 것입니다. 이렇게 하면, 합병된 두 트리의 높이가 같을 때만 전체 높이가 증가됩니다. 여기서 트리들의 높이 계산 대신 이들의 루트 노드들의 랭크를 사용합니다. 이러한 방법을 union by rank라고 부릅니다.

예제는 아래 그림을 참조하시길 바랍니다.

이렇게 설계된 union-find에서, 각 노드의 랭크는 정확히 그 노드에서 루트가 된 서브 트리의 높이입니다. 이는 루트 노드를 향해 경로를 이동함으로써, 경로를 따라 랭크의 값이 증가한다는 것을 의미합니다.
Property 1: 어떤 \(x \neq \pi(x)\)에 대해서, rank(x) < rank(\(\pi\)(x)) 이다.
랭크 k인 루트 노드는 랭크 k-1의 루트들을 가진 두 개의 트리가 병합되어 만들어집니다. 이는 귀납법에 의해서 아래의 Property 2를 다릅니다.
Property 2: 랭크 k의 임의의 루트 노드는 트리 내에서 적어도 \(2^k\)개의 노드들을 가진다.
이 특성은 루트가 없는 내부 노드들로 확장됩니다. 즉, 랭크 k의 노드는 적어도 \(2^k\)개의 자식 노드를 갖습니다. 결국 모든 내부 노드들은 한때는 루트였으며, 그 이후로 랭크나 그 노드의 하위 노드 집합은 변경되지 않습니다. 게다가, 랭크가 k인 다른 노드들은 공통의 자식 노드를 가질 수 없습니다. Property 1에 의해서 모든 요소는 랭크 k의 부모가 최대 하나만 가지기 때문입니다. 이는 다음의 Property를 의미합니다.
Property 3: 만약 전체적으로 n개의 요소가 있는 경우, 랭크 k에는 최대 \(\frac{n}{2^k}\)개의 노드들이 있다.
마지막 특성은 결정적으로 최대 rank가 \(\log n\)임을 의미합니다. 따라서 모든 트리의 높이는 \(\log n\)보다 작거나 같으며 이는 union-find의 실행 시간의 상한이 됩니다.
Path compressions
크루스칼 알고리즘의 총 실행 시간은 간선들의 정렬 시간 \(O(|E|\log |V|)\)와 알고리즘의 나머지 부분에서 사용되는 union-find 연산에 소요되는 \(O(|E|\log |V|)\)를 더한 값입니다. 따라서 데이터 구조를 더 효율적으로 만들 필요는 없어보입니다.
하지만, 만약 간선들이 정렬되어 주어진 경우에는 어떨까요? 또는 가중치가 작아서 선형 시간(\(O(|E|)\))에 정렬이 수행될 수 있다면 어떨까요? 그렇다면 union-find 자료구조 부분에서 병목 현상이 발생하게 될 것이고, union-find의 연산의 속도를 \(\log n\) 이상으로 향상시킨다는 생각은 유용합니다. 이렇게 향상된 자료구조는 결과적으로 다른 어플리케이션에서도 유용합니다.
그러나 어떻게 union과 find의 성능을 \(\log n\)보다 빠르게 수행할 수 있을까요? 정답은 데이터 구조를 좋은 모양으로 유지하도록 조금 더 주의하는 것입니다.
트리를 가능한 한 짧게 유지하기 위해 union-find의 집합을 관리하는 find 연산을 수정하여 조금 더 효율적으로 개선할 수 있습니다. find 연산이 실행되는 동안 트리를 짧게 유지하도록 하는데, 일련의 부모 포인터가 트리의 루트까지 따라갈 때 이러한 모든 포인터를 변경하여 루트를 직접 가리키게 합니다 (아래 그림 참조).

이러한 path compressions(경로 압축) 휴리스틱은 find에 대한 필요한 시간만 약간 증가시키며, 코딩하기도 쉽습니다.
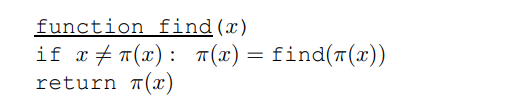
이러한 단순한 수정을 통한 이득은 순간보다는 긴 기간의 측면에서 얻을 수 있고, 그 이득을 살펴보기 위해서는 특별한 종류의 분석이 필요합니다. 비어 있는 자료 구조부터 시작하여 find와 union의 연산들의 시퀀스를 살펴보고 연산당 평균 시간을 결정합니다. 이렇게 향상된 코스트는 \(O(\log n)\)보다는 감소하고, \(O(1)\)보다는 약간 더 큰 것으로 나타납니다.
C++ 구현

위 이미지에서 나타내는 무향 그래프에서 MST를 찾도록 구현했습니다. 여기서 각 노드는 영문자로 표현되는데, 코드에서는 숫자 0부터 시작하도록 하였습니다. 그리고 간선을 나타내는 EDGE 구조체를 사용하며, 이 구조체 배열을 간선의 가중치에 대해 오름차순으로 정렬하기 위해 < 연산자를 구현하였습니다. 그리고 union-find 자료 구조를 위한 union_find 클래스를 구현하여 필요한 연산들을 사용합니다.
#include <iostream>
#include <vector>
#include <algorithm>
struct EDGE {
int u, v, w;
EDGE(int u, int v, int w) : u(u), v(v), w(w) {}
bool operator<(const EDGE& comp) const {
return w < comp.w;
}
};
// union-find structure
class union_find final
{
public:
union_find(const int N) : number_of_V(N) {
parents.resize(N, 0);
}
void makeset(int u) {
parents[u] = u;
}
int find(int u) {
if (u != parents[u])
parents[u] = find(parents[u]);
return parents[u];
}
void merge(int u, int v) {
u = find(u);
v = find(v);
if (u == v) return;
parents[v] = u;
}
private:
int number_of_V{ 0 };
std::vector<int> parents{};
};
std::vector<EDGE> kruskal(std::vector<EDGE>& edges, const int N)
{
union_find uf(N);
for (int i = 0; i < N; i++) {
uf.makeset(i);
}
std::vector<EDGE> ret;
sort(edges.begin(), edges.end());
for (auto& edge : edges) {
if (uf.find(edge.u) != uf.find(edge.v)) {
ret.push_back(edge);
uf.merge(edge.u, edge.v);
}
}
return ret;
}
int main(void)
{
std::vector<EDGE> edges;
int N = 6;
edges.push_back({ 0, 1, 2 }); // A-B, 2
edges.push_back({ 0, 2, 1 }); // A-C, 1
edges.push_back({ 1, 2, 2 }); // B-C, 2
edges.push_back({ 1, 3, 1 }); // B-D, 1
edges.push_back({ 2, 3, 2 }); // C-D, 2
edges.push_back({ 2, 4, 3 }); // C-E, 3
edges.push_back({ 3, 4, 3 }); // D-E, 3
edges.push_back({ 3, 5, 4 }); // D-F, 4
edges.push_back({ 4, 5, 1 }); // E-F, 1
auto result = kruskal(edges, N);
std::cout << "-- Results --\n";
int total_weights = 0;
for (auto& edge : result) {
std::cout << static_cast<char>(edge.u + 'A') << "-" << static_cast<char>(edge.v + 'A') << ", weight=" << edge.w << std::endl;
total_weights += edge.w;
}
std::cout << "MST's total weight = " << total_weights << std::endl;
}위 코드를 실행하면 아래의 결과를 얻을 수 있습니다.
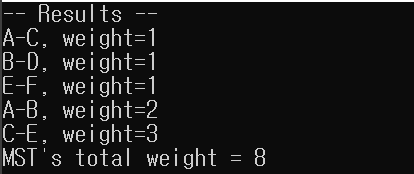
여기서 찾은 MST는 유일한 답은 아니며, 정렬 방식에 따라서 다른 MST가 나올 수도 있습니다.
그리고 kruskal 함수에서 edges들을 순회할 때, N-1개의 간선을 모두 뽑았다면 더 이상 진행하지 않고 알고리즘을 종료함으로써 불필요한 순회를 줄일 수도 있습니다. 이는 MST에 간선을 추가할 때마다 카운트하도록 하여 구현할 수 있습니다.
'Data Structure & Algorithm > 알고리즘' 카테고리의 다른 글
| [DP] Knapsack Problem (0-1 Knapsack) (0) | 2022.04.14 |
|---|---|
| 동적 프로그래밍 (Dynamic Programming) (0) | 2022.04.13 |
| 피보나치 수열 (0) | 2021.10.26 |
| 보이어-무어-호스풀 알고리즘(Boyer-Moore-Horspool Algorithm) (0) | 2021.10.12 |
| [그래프] 플로이드-워셜 알고리즘(Floyd-Warshall Algorithm) (0) | 2021.10.11 |




댓글