References
- 리얼월드 알고리즘
Contents
- 플로이드-워셜 알고리즘
다익스트라 알고리즘과 벨만-포드 알고리즘에 이어서 또 다른 최단 경로 알고리즘인 플로이드-워셜 알고리즘에 대해서 알아보겠습니다.
2021.10.07 - [Data Structure & Algorithm/알고리즘] - [그래프] 다익스트라 알고리즘(Dijkstra's algorithm)
[그래프] 다익스트라 알고리즘(Dijkstra's algorithm)
References 리얼월드 알고리즘 Contents 다익스트라(데이크스트라) 알고리즘 구현 임의의 원소에 접근해 값 갱신(update)이 가능한 Heap(우선순위 큐) 구현 음의 가중치는 사용 불가 그래프의 지름 C++로
junstar92.tistory.com
2021.10.10 - [Data Structure & Algorithm/알고리즘] - [그래프] 벨만-포드 알고리즘(Bellman-Ford Algorithm)
[그래프] 벨만-포드 알고리즘(Bellman-Ford Algorithm)
References 리얼월드 알고리즘 Contents 벨만-포드 알고리즘 큐 기반 벨만-포드 알고리즘 음의 가중치 순환 2021.10.07 - [Data Structure & Algorithm/알고리즘] - [그래프] 다익스트라 알고리즘(Dijkstra's algo..
junstar92.tistory.com
플로이드-워셜 알고리즘은 그래프의 모든 쌍 사이에서 최단 경로를 계산하는 알고리즘입니다. 다익스트라 알고리즘이나 벨만-포드 알고리즘보다는 일반적으로 조금 더 느리지만, 밀도 높은 그래프에서 잘 동작하고, 음의 가중치를 갖는 그래프에서도 잘 동작합니다. 무엇보다 알고리즘을 위해서 특수한 자료 구조가 필요하지 않기 때문에 구현하기가 매우 간단하다는 특징이 있습니다.
그럼 바로 플로이드-워셜 알고리즘은 어떻게 최단 거리를 찾는지 살펴보도록 하겠습니다.

이 알고리즘은 i 노드에서 j 노드로 가는데, 중간에 k 노드로 우회해서 가면 거리가 얼마가 되는지 모두 검사하는 컨셉으로 수행됩니다. 예를 들면, 위 그래프에서 2번 노드에서 1번 노드로 가는데, 어느 노드를 거쳐서 가는 것이 더 짧은 경로로 가는지 체크하는 것이죠.
그래프에서 i 노드에서 j 노드로 가는 모든 경로는 아래와 같습니다. 알고리즘을 수행하면서 아래의 경로를 모두 체크하게 되는 것이죠.

알고리즘이 실제로 하는 것은 이 그래프의 문제에 대한 해법의 일부를 계산하고 이를 점진적으로 결합하여 전체 해법에 도달하는 것이라고 볼 수 있습니다. 가능하다면 더 짧은 경로를 찾아서 결합하여 최종적으로 가장 짧은 경로를 만들게 됩니다. 이렇게 문제의 일부를 해결하고 최종 답에 이르고자 부분적인 해법을 결합하는 방법은 동적 프로그래밍(dynamic programming; DP)라고 합니다.
알고리즘은 다음과 같습니다.

정점의 개수가 \(|V|\)개인 그래프를 입력받아서 모든 노드 쌍의 최단 거리와 선행 노드를 반환합니다.
1행에서 10행까지 초기화를 수행하는데, \(|V| \times |V|\) 크기를 가진 pred와 dist 배열에 적절한 값을 설정합니다.
dist[i, j]의 경우에는 i 노드에서 j 노드까지 간선으로 직접 연결되어 있다면, 그 간선의 가중치로 설정해주고 직접 연결되어 있지 않다면 \(\infty\)로 초기화합니다. pred[i, j]의 경우에는 간선이 직접적으로 연결되어 있다면 노드 j에 도달하기 전 선행 노드를 i로 설정해줍니다.
그리고 11행부터 최단 경로 탐색을 시작하는데, 3중 for문으로 이루어져 있습니다.
가장 외부의 루프가 노드 i에서 노드 j로의 경로를 찾을 때, 중간 노드인 k를 반복하는데, 0부터 \(|V| - 1\) 노드까지 반복하게 됩니다. 중간 루프가 시작 노드인 i를 반복하고, 가장 내부의 루프가 도착 노드인 j를 반복합니다.
14행에서 이제 이전까지 살펴봤던 i 노드에서 j 노드까지의 거리가 k 노드를 거쳐서 i에서 j 노드로 가는 경로의 크기보다 큰 지 비교를 하게 됩니다. 만약 k 노드를 거쳐서 j 노드까지 가는데 거리가 더 짧다면, dist[i, j]와 pred[i, j]를 갱신하게 됩니다.
C++ 구현
큐와 같은 다른 자료 구조가 필요하지 않기 때문에, 매우 간단합니다.
먼저 그래프 자료구조를 나타내기 위해서 다익스트라 알고리즘과 벨만-포드 알고리즘에서 사용했던 자료구조를 그대로 사용했습니다. init_graph에서 정점의 개수를 입력받아서 그래프를 초기화하고, add_edge를 통해 해당 그래프에 존재하는 간선을 추가해줍니다.
/* FloydWarshall.hpp */
#ifndef __FLOYDWARSHALL_HPP__
#define __FLOYDWARSHALL_HPP__
#include <vector>
#define INF 123456789
typedef struct _edge {
int destination;
int weight;
} EDGE;
typedef struct _graph {
int num_node;
std::vector<std::vector<EDGE>> edge;
} GRAPH;
void init_graph(GRAPH& graph, int num_node);
void add_edge(GRAPH& graph, int u, int v, int w, bool direction = false);
std::pair<std::vector<std::vector<int>>, std::vector<std::vector<int>>> floydwarshall(GRAPH& graph);
#endif
21행의 floydwarshall 함수에서 알고리즘을 수행하여 최단 경로와 선행 노드의 배열을 반환합니다.
std::pair<std::vector<std::vector<int>>, std::vector<std::vector<int>>> floydwarshall(GRAPH& graph)
{
std::vector<std::vector<int>> dist(graph.num_node, std::vector<int>(graph.num_node, INF));
std::vector<std::vector<int>> pred(graph.num_node, std::vector<int>(graph.num_node, -1));
for (int i = 0; i < graph.num_node; i++)
{
dist[i][i] = 0;
for (auto& edge : graph.edge[i]) {
int& j = edge.destination;
int& w = edge.weight;
dist[i][j] = w;
pred[i][j] = i;
}
}
for (int k = 0; k < graph.num_node; k++) {
for (int i = 0; i < graph.num_node; i++) {
for (int j = 0; j < graph.num_node; j++) {
if ((dist[i][k] != INF || dist[j][k] != INF) && (dist[i][j] > dist[i][k] + dist[k][j])) {
dist[i][j] = dist[i][k] + dist[k][j];
pred[i][j] = pred[k][j];
}
}
}
}
return { dist, pred };
}3 ~ 15 lines까지 초기화를 수행합니다. i 노드에서 j 노드까지 직접 연결되는 간선이 존재한다면, 값을 해당 가중치로 업데이트하고 선행 노드도 설정해줍니다.
그리고 17 line부터 반복이 수행되는데, 현재 dist[i][j]의 값은 지금까지 찾은 최단 경로의 거리를 담고 있습니다.
여기서 20 line에서 k 노드로 우회해서 i 에서 j 노드로 가는 경로가 더 빠른지 체크하고, 더 빠르다면 dist[i][j]가 dist[i][k] + dist[k][j]로 갱신됩니다.
(만약 dist[i][k]나 dist[k][j]가 \(\infty\)라면 더하여 비교하는 게 의미가 없기 때문에, \(\infty\)인지 먼저 체크하고 무한대가 아니라면 비교를 수행합니다.)
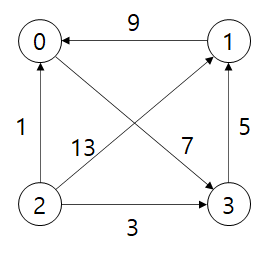
위 예시를 가지고 위 코드를 실행해보면 다음과 같습니다.
#include <iostream>
#include <stdio.h>
#include "FloydWarshall.hpp"
int main(void) {
GRAPH graph;
init_graph(graph, 4);
add_edge(graph, 0, 3, 7);
add_edge(graph, 1, 0, 9);
add_edge(graph, 2, 0, 1);
add_edge(graph, 2, 1, 13);
add_edge(graph, 2, 3, 3);
add_edge(graph, 3, 1, 5);
auto result = floydwarshall(graph);
/* shortest path value */
for (int i = 0; i < graph.num_node; i++) {
for (int j = 0; j < graph.num_node; j++) {
printf(" %3d ", result.first[i][j]);
}
printf("\n");
}
return 0;
}
시간복잡도
이 알고리즘은 3중 for문으로 수행되기 때문에 이 알고리즘의 시간 복잡도는 V개의 정점이 존재할 때, \(O(|V|^3)\) 입니다.
모든 정점 쌍의 최단 거리를 구하기 때문에, 다익스트라 알고리즘은 \(O(|V||E|log|V|)\) 이므로, 다익스트라가 약간 더 빠르다고 할 수 있지만, 벨만-포드의 경우에는 \(O(|V|^2|E|)\) 이고, 보통 정점의 수보다 간선의 수가 더 많기 때문에 플로이드-워셜이 조금 더 빠르다고 볼 수 있습니다.
전체 코드는 아래 깃헙에서 확인할 수 있습니다.
https://github.com/junstar92/DataStructure_Algorithm/tree/master/Algorithm/FloydWarshall
GitHub - junstar92/DataStructure_Algorithm
Contribute to junstar92/DataStructure_Algorithm development by creating an account on GitHub.
github.com
'Data Structure & Algorithm > 알고리즘' 카테고리의 다른 글
| 피보나치 수열 (0) | 2021.10.26 |
|---|---|
| 보이어-무어-호스풀 알고리즘(Boyer-Moore-Horspool Algorithm) (0) | 2021.10.12 |
| [그래프] 벨만-포드 알고리즘(Bellman-Ford Algorithm) (0) | 2021.10.10 |
| [그래프] 다익스트라 알고리즘(Dijkstra's algorithm) (0) | 2021.10.07 |
| [그래프] 가중치 그래프와 임계 경로(Critical Path) (0) | 2021.10.06 |




댓글