References
- 리얼월드 알고리즘
Contents
- 벨만-포드 알고리즘
- 큐 기반 벨만-포드 알고리즘
- 음의 가중치 순환
2021.10.07 - [Data Structure & Algorithm/알고리즘] - [그래프] 다익스트라 알고리즘(Dijkstra's algorithm)
[그래프] 다익스트라 알고리즘(Dijkstra's algorithm)
References 리얼월드 알고리즘 Contents 다익스트라(데이크스트라) 알고리즘 구현 임의의 원소에 접근해 값 갱신(update)이 가능한 Heap(우선순위 큐) 구현 음의 가중치는 사용 불가 그래프의 지름 C++로
junstar92.tistory.com
이전 게시글에서 다룬 최단 경로 알고리즘인 다익스트라 알고리즘에 이어서, 다른 최단 경로 알고리즘인 벨만-포드 알고리즘에 대해서 알아보겠습니다.
벨만-포드 알고리즘은 라우팅 정보 프로토콜(RIP)에서 라우터들 사이에서 경로를 배정하는데 사용되는데, 네트워크는 저도 잘 모르는 분야이므로... 매우 간략하게 정리하면 라우터에 패킷을 보낼 때 각 자율 시스템(autonomous system) 내의 라우터들 사이에서 경로를 배정할 때 사용된다고 합니다.
네트워크에 관해서는... 기회가 된다면 나중에 더 살펴보도록 하고, 오늘 글의 목적인 벨만-포드 알고리즘에 대해서 바로 살펴보겠습니다.
벨만-포드 알고리즘
RIP에서는 시작 노드로부터의 최단 경로뿐만 아니라 임의의 노드 두 쌍 사이의 모든 최단 경로를 구하므로, 오리지널 벨만-포드 알고리즘의 업그레이드 버전이라고 할 수 있습니다. (RIP는 모든 쌍의 최단 경로 문제를 해결합니다.)
우선 업그레이드 버전이 아닌 벨만-포드 알고리즘의 기본 버전을 먼저 살펴보겠습니다.
Input과 Output은 다익스트라 알고리즘과 동일합니다. 최단 경로에 있는 각 노드의 선행 노드 정보를 유지하는데 배열 pred를 사용하고, 최단 경로의 값을 유지하는 데 dist를 사용합니다.

벨만-포드 알고리즘은 1~8행에서 자료 구조를 초기화하며 시작 노드까지의 경로를 제외한 다른 최단 경로가 없는 상황으로 설정합니다. 따라서 어느 노드로 선행 노드를 갖지 않고(pred[i] = -1), 길이가 0으로 설정되는 시작 노드에서 시작 노드로 가는 경로를 제외하고 모든 최단 경로의 길이는 \(\infty\)로 설정됩니다. (물론 컴퓨터는 무한대가 존재하지 않기 때문에 절대 존재하지 않는 최대값으로 설정하면 됩니다.)
초기화 이후에는 끊임없이 증가하는 간선 수의 최단 경로를 검사합니다.
이 말이 무슨 의미냐면, 첫 반복문에서는 시작 노드에서 간선 하나로 도달할 수 있는 모든 최단 경로가 발견되어 갱신되고, 두 번째 반복에서는 시작 노드에서 최대 2개의 간선으로 도달 가능한 모든 최단 경로가 갱신됩니다.
일반화하면, k번째 반복에서 시작 노드에서 최대 k개의 간선으로 도달 가능한 최단 경로를 찾게 됩니다.
최대 수의 간선을 갖는 경로는 그래프의 모든 노드를 정확히 한 번씩 포함하므로 \(|V| - 1\)개의 간선을 가지게 되며, 즉, \(|V| - 1\)번 반복하면 시작 노드에서의 모든 노드까지의 최단 경로를 찾게 됩니다.
\(|V|-1\)보다 더 많은 간선을 갖는 최단 경로는 없기 때문입니다.(만약 존재한다면 사이클이 존재한다는 뜻입니다.)

이전 게시글에서 살펴봤던 위의 그래프 예제로 벨만-포드 알고리즘이 어떻게 최단 경로를 추적하는지 살펴보겠습니다.
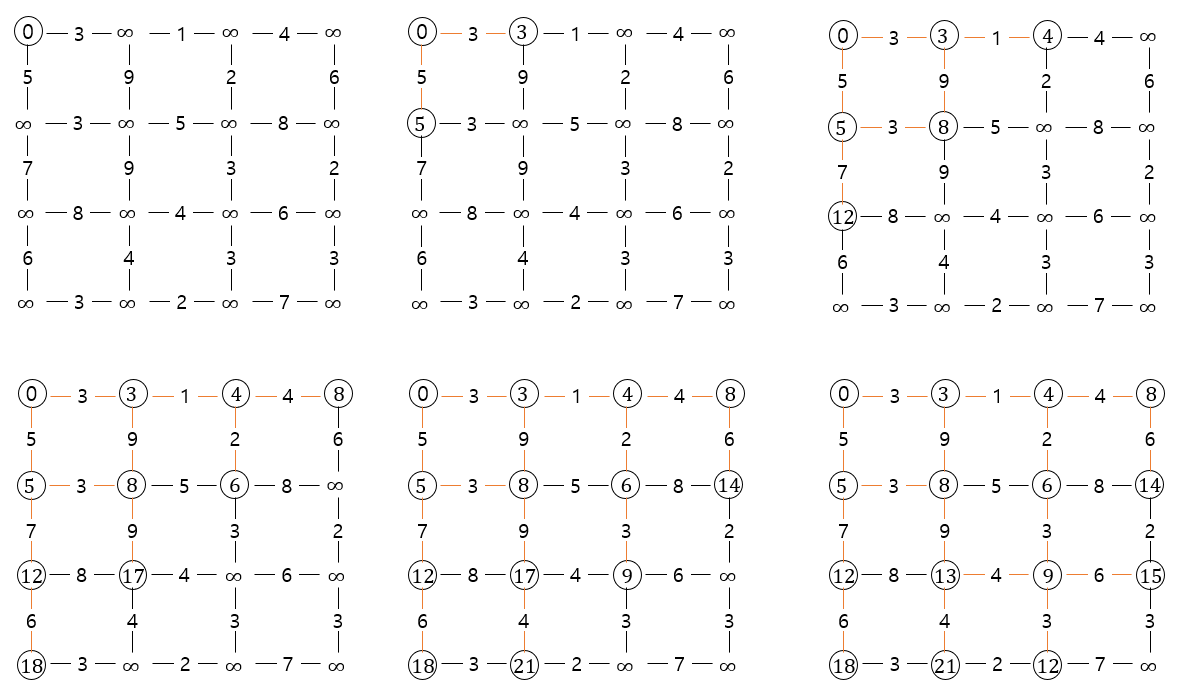
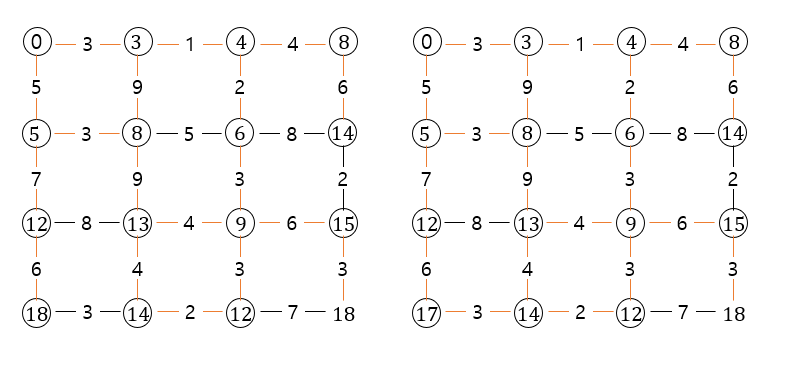
첫 번째 그림(왼쪽위)에는 간선을 하나도 갖지 않은 경로를 보여주고, 두 번째 그림(왼쪽중간)에는 하나의 간선을 갖는 경로, 세 번째 그림(오른쪽위)에는 두 개의 간선을 갖는 경로를 보여주고 있습니다.
그리고 마지막 경로(세번째 오른쪽)은 최대 7개의 간선을 갖는 경로가 포함되어 있습니다.
벨만-포드 알고리즘은 경로 사이의 선택을 포함하며, 해당 반복 내에서 최선의 선택을 합니다.
3번째 그림(오른쪽위)을 보면, 노드 (1, 1)까지 2개의 간선을 갖는 2개의 경로((1,0) -> (1,1)과 (0,1) -> (1,1))가 있는데, 가장 짧은 (0,1) -> (1,1) 경로를 선택합니다.
5번째 그림(2번째줄 중앙)에서 노드 (2, 2)를 노드 (2, 1)을 통해서 가는 대신 노드 (1, 2)를 통해 가는 것을 선택하여 최단 거리를 갱신합니다.
한 노드의 최단 경로는 알고리즘이 끝날 때까지 계속 변할 수 있으며, 게다가 마지막 그림에서 모든 노드를 다 살펴본 후에도 더 많은 간선을 갖는 더 좋은 경로가 여전히 있을 수 있습니다. 마지막 그림에서는 노드 (3, 0)이 노드 (3, 1)을 경유하여 더 짧은 경로를 갖게 될 때, 3개의 간선을 갖는 이전 경로 \((0,0) \rightarrow (1,0) \rightarrow (2,0) \rightarrow (3,0)\) 대신에, 새로운 경로는 7개의 간선을 포함하고 \((0,0) \rightarrow (0,1) \rightarrow (0,2) \rightarrow (1,2) \rightarrow (2,2) \rightarrow (3,2) \rightarrow (3,1) \rightarrow (3,0)\) 순으로 연결됩니다.
구현
다익스트라 알고리즘와 거의 유사하며, 루프 부분에서 우선순위 큐를 사용하는 것이 아닌 for문을 사용합니다.
우선 그래프 자료구조를 위해서 구조체를 따로 만들었는데, 정점의 개수와 각 정점에서의 간선의 정보를 저장하는 구조체입니다. 그리고 그래프 자료구조 초기화와 간선 추가를 위해서 함수를 정의해주었습니다.
typedef struct _edge {
int destination;
int weight;
} EDGE;
typedef struct _graph {
int num_node;
std::vector<std::vector<EDGE>> edge;
} GRAPH;
void init_graph(GRAPH& graph, int num_node)
{
graph.num_node = num_node;
graph.edge.resize(num_node, {});
}
void add_edge(GRAPH& graph, int u, int v, int w, bool direction)
{
graph.edge[u].push_back({ v, w });
if (direction == false)
graph.edge[v].push_back({ u, w });
}
다음으로 벨만-포드 알고리즘 구현입니다.
std::pair<std::vector<int>, std::vector<int>> bellmanford(GRAPH& graph, int src)
{
std::vector<int> pred(graph.num_node, -1);
std::vector<int> dist(graph.num_node, INF);
dist[src] = 0;
for (int i = 0; i < graph.num_node - 1; i++) {
for (int u = 0; u < graph.num_node; u++) {
for (auto& edge : graph.edge[u]) {
int& v = edge.destination;
int& w = edge.weight;
if ((dist[u] != INF) && (dist[v] > dist[u] + w)) {
dist[v] = dist[u] + w;
pred[v] = u;
}
}
}
}
return { pred, dist };
}2~4행은 초기화 부분입니다. 각 노드의 선행 노드를 모두 -1로 초기화하고, 각 노드까지의 거리는 시작 노드에서 시작 노드 거리인 0을 제외하고는 \(\infty\)로 설정하였습니다.
그리고 6행부터 루프가 시작되는데, 가장 바깥의 루프는 총 \(|V|-1\)번 반복하며, 그 내부에서 모든 간선을 훑어보기 시작합니다. 한 번도 갱신된 적이 없는 노드는 진행하지 않기 때문에, 반복을 수행할 때마다 최단 경로에 포함되는 최대 간선 개수가 하나씩 증가하게 됩니다.
그럼 정상적으로 동작하는지 위 예시 그래프를 가지고 확인해보겠습니다.
#include <iostream>
#include <stdio.h>
#include "BellmanFord.hpp"
int main(void) {
GRAPH graph;
init_graph(graph, 16);
add_edge(graph, 0, 1, 3);
add_edge(graph, 0, 4, 5);
add_edge(graph, 1, 2, 1);
add_edge(graph, 1, 5, 9);
add_edge(graph, 2, 3, 4);
add_edge(graph, 2, 6, 2);
add_edge(graph, 3, 7, 6);
add_edge(graph, 4, 5, 3);
add_edge(graph, 4, 8, 7);
add_edge(graph, 5, 6, 5);
add_edge(graph, 5, 9, 9);
add_edge(graph, 6, 7, 8);
add_edge(graph, 6, 10, 3);
add_edge(graph, 7, 11, 2);
add_edge(graph, 8, 9, 8);
add_edge(graph, 8, 12, 6);
add_edge(graph, 9, 10, 4);
add_edge(graph, 9, 13, 4);
add_edge(graph, 10, 11, 6);
add_edge(graph, 10, 14, 3);
add_edge(graph, 11, 15, 3);
add_edge(graph, 12, 13, 3);
add_edge(graph, 13, 14, 2);
add_edge(graph, 14, 15, 7);
int start_node = 0;
auto result = bellmanford(graph, start_node);
printf("----- distance from start node %d -----\n\n", start_node);
for (int i = 0; i < graph.num_node; i++) {
printf(" %3d ", result.second[i]);
if ((i + 1) % 4 == 0)
printf("\n");
}
printf("\n");
return 0;
}
위에서 추적한 것과 동일한 결과를 보여주고 있습니다.
전체 코드는 아래 깃헙에서 확인하실 수 있습니다.
https://github.com/junstar92/DataStructure_Algorithm/tree/master/Algorithm/BellmanFord
GitHub - junstar92/DataStructure_Algorithm
Contribute to junstar92/DataStructure_Algorithm development by creating an account on GitHub.
github.com
시간 복잡도
실행 시간 관점에서 벨만-포드 알고리즘은 초기화 부분에서 \(|V|\)번 반복합니다. 초기화는 상수 시간이 소여되는 배열에 값을 설정하는 것을 포함하여 모두 \(O(|V|)\) 시간이 걸립니다. 9~13행의 루프는 총 \(|V| - 1\)번 반복되고, 매번 그래프의 모든 간선을 조사하므로, \(O(|V| - 1)|E| = O(|V||E|)\) 시간이 소요됩니다.
그러므로 전체 알고리즘은
\[O(|V| + |V||E|) = O(|V||E|)\]
시간이 걸립니다.
위 그래프 예시의 노드는 총 16개이고, 7번째 루프에서 모든 최단 경로를 찾았다고 하더라도 알고리즘은 끝나지 않는다는 것에 주목해야합니다. 벨만-포드 알고리즘은 15번째 반복에 도달할 때까지 계속 더 많은 간선을 갖는 최단 경로를 찾으려고 합니다. 그러나 이 예제에서는 남은 루프동안 더 짧은 경로는 반복되지 않으므로 최단 경로 탐색을 멈추고 더는 진행하지 않아도 됩니다. 이는 이 알고리즘이 최적화할 여지가 있다는 것을 보여줍니다.
m개의 노드가 존재하는 그래프에서 벨만-포드 알고리즘이 i번째 반복 중에 있다고 가정해봅시다. 이러한 상황에서의 노드들의 최단 경로는 최대 i개의 간선을 가질 것입니다. 따라서, 우리는 이미 최대 i개의 간선을 갖는 경로를 찾았으므로 (i+1) 번째 반복에서는 최대 i+1개의 간선을 갖는 최단 경로는 찾게 됩니다. 그렇기 때문에 알고리즘의 각 반복에서 모든 간선을 조사하는 대신에 이전 반복에서 갱신되었던 노드들의 간선만 조사하면 됩니다.
이를 위해서 큐를 사용하여 노드를 큐에 넣으면서 반복하며 추정값을 갱신합니다. 이때 아이템이 큐에 존재하는지 알 방법이 필요한데, 쉬운 방법은 bool 배열을 사용하여 노드가 큐에 존재하면 참, 그렇지 않으면 거짓이 되게 하는 것입니다.
알고리즘은 다음과 같습니다.

코드로 구현하면 다음과 같습니다.
std::pair<std::vector<int>, std::vector<int>> bellmanford_queue(GRAPH& graph, int src)
{
std::vector<int> pred(graph.num_node, -1);
std::vector<int> dist(graph.num_node, INF);
std::vector<bool> inqueue(graph.num_node, false);
std::queue<int> q;
dist[src] = 0;
q.push(src);
inqueue[src] = true;
while (q.size() != 0) {
int u = q.front();
q.pop();
inqueue[u] = false;
for (auto& edge : graph.edge[u]) {
int& v = edge.destination;
int& w = edge.weight;
if ((dist[u] != INF) && (dist[v] > dist[u] + w)) {
dist[v] = dist[u] + w;
pred[v] = u;
if (inqueue[v] == false) {
q.push(v);
inqueue[v] = true;
}
}
}
}
return { pred, dist };
}큐가 빌 때까지 반복하고, i번째 반복에서 갱신되는 노드만 다음 반복에서 체크하게 됩니다. 이전 구현에서는 매 반복마다 모든 노드에 대해서 반복했다면, 이 경우에는 갱신되는 노드에 대해서만 체크하기 때문에 더 빠르다고 볼 수 있습니다.
이 알고리즘은 Short Path Faster Algorithm(SPFA)라고 불리기도 하고, 최악의 경우에는 \(O(|V||E|)\)의 시간 복잡도를 가지지만, 평균적으로 \(O(|V| + |E|)\)의 시간 복잡도를 보여주는 매우 효율적인 알고리즘으로 알려져있습니다.
음의 가중치와 순환
다익스트라 알고리즘과 비교했을 때 벨만-포드 알고리즘을 무조건 선택해야하는 경우가 있을 수 있습니다. 바로 음의 가중치가 존재할 때인데, 다익스트라 알고리즘의 경우에는 잘못된 결과를 도출하지만, 벨만-포드 알고리즘은 음의 가중치를 적절하게 대처할 수 있습니다. 실제로 아래의 그래프에 벨만-포드 알고리즘을 적용하면 올바른 결과를 얻을 수 있습니다.

위 그래프에 대해서 벨판-포드 알고리즘을 적용하면 다음과 같은 순서로 최단 거리를 찾게 됩니다.

이제 위처럼 음의 가중치뿐만 아니라 음의 순환을 포함한다면 어떻게 될지 살펴보겠습니다.

처음 살펴봤던 벨만-포드 기본 알고리즘을 수행하면 \(|V|\) 반복 후에 멈출 것이고 의미없는 결과를 출력하게 됩니다. 이는 음의 가중치가 있는 순환을 따라가는 최단 경로는 가중치 \(-\infty\)를 갖는 순환을 따라 영원히 순환하는 경로이기 때문입니다. 큐 기반 알고리즘은 절대 멈추지 않으므로 더 좋지 않습니다. 만약 음의 가중치 순환을 만난다면 큐에 해당 노드를 추가하고 추출하는 무한 루프에 빠지게 됩니다.
그렇기 때문에 큐 기반의 알고리즘에서 음의 순환을 종료하려면 부차적인 작업을 해야합니다.
만약 \(|V| - 1\)개보다 많은 간선을 갖는 경로를 발견한다면 순환을 탐지할 수 있습니다. 이는 \(|V|\)개의 노드를 갖는 그래프에서 가장 긴 경로는 모든 노드를 포함하며 \(|V| - 1\)개의 간선을 갖기 때문입니다. 이보다 더 많은 간선을 갖는 최단 경로가 존재한다면 이는 이미 방문했던 노드를 다시 방문한다는 것을 의미하고 결국 순환이 존재한다는 의미가 됩니다.
벨만-포드 알고리즘 이면에 있는 기본 아이디어는 간선의 수가 증가하는 경로를 조사하는 것임을 기억합시다. 초기에 시작 노드에서 시작할 때 0개의 간선의 경로를 갖고, 큐에 있는 시작 노드의 이웃 노드들을 추가할 때 1개의 간선으로 된 경로를 갖습니다. 그리고 이 이웃 노드의 이웃 노드들을 추가하면 2개의 간선으로 된 경로를 갖게 됩니다.
문제는 한 이웃 노드들의 집합에 대한 처리를 중단하고 언제 또 다른 이웃 노드의 집합을 진행할지 어떻게 아는가 입니다. 우리는 이미 이와 같은 작업이 \(|V| - 1\)번 일어나면 알고리즘이 종료되어야 한다는 것을 알고 있습니다 !
벨만-포드 알고리즘 기본형과 큐 기반에서 모두 음의 순환이 존재하는지 체크할 수 있는데, 코드는 다음과 같습니다.
기본형 + nc(negative cycle) 체크
std::pair<std::pair<std::vector<int>, std::vector<int>>, bool> bellmanford_nc(GRAPH& graph, int src)
{
std::vector<int> pred(graph.num_node, -1);
std::vector<int> dist(graph.num_node, INF);
dist[src] = 0;
for (int i = 0; i < graph.num_node; i++) {
for (int u = 0; u < graph.num_node; u++) {
for (auto& edge : graph.edge[u]) {
int& v = edge.destination;
int& w = edge.weight;
if ((dist[u] != INF) && (dist[v] > dist[u] + w)) {
if (i == graph.num_node - 1) {
return { {pred, dist}, false };
}
dist[v] = dist[u] + w;
pred[v] = u;
}
}
}
}
return { {pred, dist}, true };
}기본형에서 외부 for문의 반복 횟수가 하나 증가했고, 만약 반복 횟수가 \(|V| - 1\)가 지나서도 최단 경로가 갱신된다면 순환이 발생했다는 것을 뜻하므로, false를 반환합니다. 만약 순환이 없다면 true를 반환하게 됩니다.
큐 기반 + nc(negative cycle) 체크
std::pair<std::pair<std::vector<int>, std::vector<int>>, bool> bellmanford_queue_nc(GRAPH& graph, int src)
{
std::vector<int> pred(graph.num_node, graph.num_node);
std::vector<int> dist(graph.num_node, INF);
std::vector<bool> inqueue(graph.num_node, false);
std::queue<int> q;
dist[src] = 0;
q.push(src);
inqueue[src] = true;
q.push(graph.num_node);
int i = 0;
while ((q.size() != 1) && (i < graph.num_node)) {
int u = q.front();
q.pop();
if (u == graph.num_node) {
i += 1;
q.push(graph.num_node);
}
else {
inqueue[u] = false;
for (auto& edge : graph.edge[u]) {
int& v = edge.destination;
int& w = edge.weight;
if ((dist[u] != INF) && (dist[v] > dist[u] + w)) {
dist[v] = dist[u] + w;
pred[v] = u;
if (inqueue[v] == false) {
q.push(v);
inqueue[v] = true;
}
}
}
}
}
return { {pred, dist}, i < graph.num_node };
}큐 기반 알고리즘에서는 특수한 센티널(sentinal) 값을 사용하여 해결할 수 있습니다. 일반적으로 센티널 값은 어떤 특정 이벤트가 유효하지 않음을 알려주는 값이고, 여기서는 숫자 \(|V|\)를 센티널 값으로 사용했습니다. (노드가 0부터 \(|V|-1\)까지 있고, \(|V|\)는 없기 때문)
특히 숫자 \(|V|\)는 시작 노드에서 떨어져 있는 같은 수의 간선을 갖는 이웃 노드 집합의 경계에서 큐를 구분하는 데 사용합니다. 즉 한 노드의 이웃 노드들을 반복하는게 \(|V|\)번 반복된다면 \(|V| - 1\)개의 간선보다 더 많은 간선을 갖는 최단 경로가 존재한다는 의미이고, 이는 음의 순환이 발생했다는 것을 뜻하게 됩니다.
코드를 살펴보면 기존 큐 기반 코드에서 어떻게 센티널값을 적용했는지 알 수 있습니다.
주의해야 할 점은 센티널 값이 큐에 들어가 있기 때문에, 센티널 값만 큐에 남아있을 때까지 반복해야 합니다.(0이 아닌 1임)
실제로 잘 출력하는지 확인하기 위해서 테스트를 해봅시다.
#include <iostream>
#include <stdio.h>
#include "BellmanFord.hpp"
int main(void) {
GRAPH graph;
init_graph(graph, 5);
add_edge(graph, 0, 1, 1, true);
add_edge(graph, 1, 2, 2, true);
add_edge(graph, 2, 3, 3, true);
add_edge(graph, 3, 1, -6, true);
add_edge(graph, 3, 4, 4, true);
add_edge(graph, 4, 0, 5, true);
int start_node = 0;
auto result = bellmanford_queue_nc(graph, start_node);
printf("----- distance from start node %d -----\n\n", start_node);
for (int i = 0; i < graph.num_node; i++) {
printf(" %3d ", result.first.second[i]);
}
printf("\n");
printf("\n Negative Cycle : %s", result.second ? "false" : "true");
return 0;
}큐 기반 nc 체크 버전을 돌려보면 다음과 같습니다.

순환을 돌기 전까지 최단 거리를 잘 나타내고 있는 것 같습니다.
다만, 기본 알고리즘에 nc 체크를 넣으면, Cycle을 잘 체크하지만, 매 루프마다 모든 간선을 돌아보기 때문에 이미 음의 순환이 적용된 다른 값이 출력되고 있습니다.

마찬가지로 전체코드는 깃헙 참조바랍니다 !
https://github.com/junstar92/DataStructure_Algorithm/tree/master/Algorithm/BellmanFord
GitHub - junstar92/DataStructure_Algorithm
Contribute to junstar92/DataStructure_Algorithm development by creating an account on GitHub.
github.com
'Data Structure & Algorithm > 알고리즘' 카테고리의 다른 글
| 보이어-무어-호스풀 알고리즘(Boyer-Moore-Horspool Algorithm) (0) | 2021.10.12 |
|---|---|
| [그래프] 플로이드-워셜 알고리즘(Floyd-Warshall Algorithm) (0) | 2021.10.11 |
| [그래프] 다익스트라 알고리즘(Dijkstra's algorithm) (0) | 2021.10.07 |
| [그래프] 가중치 그래프와 임계 경로(Critical Path) (0) | 2021.10.06 |
| [그래프] 위상 정렬 Topological Sort (0) | 2021.10.05 |




댓글