References
- 리얼월드 알고리즘
Contents
- 가중치 그래프(weighted graph)
- 임계 경로(critical path)
가중치 그래프 Weighted Graph
이전 글들에서 그래프 자료구조와 위상 정렬에 대해서 살펴봤습니다.
2021.10.04 - [Data Structure & Algorithm/자료구조] - [자료구조] Directed Graph
2021.10.05 - [Data Structure & Algorithm/알고리즘] - [그래프] 위상 정렬 Topological Sort
이 글들에서 정점과 이들 사이를 연결하는 간선으로 표현하는 그래프를 사용했는데, 숫자로 된 가중치를 각 간선에 부옇여 그래프를 확장할 수 있습니다. 이러한 그래프를 가중치 그래프(weighted graph)라고 합니다.
가중치 그래프는 비가중치 그래프를 일반화한 것인데, 비가중치 그래프는 모든 간선의 가중치가 동일해서 생략한 가중치 그래프로 볼 수 있기 때문입니다.
가중치 그래프는 더 많은 정보를 표현할 수 있어서 유용합니다. 그래프가 도로망을 나타낸다면 가중치는 거리 또는 두 지점 사이를 여행하는데 걸리는 시간일 수 있습니다.
아래에 가중치를 적용한 방향 그래프가 있습니다.

가중치 그래프는 비가중치 그래프와 유사하게 표현할 수 있습니다.
인접 행렬로 나타낸다면, 가중치 그래프의 인접 행렬은 엔트리로 간선들의 가중치를 갖거나 연결되지 않은 엔트리들에 대해서는 특수한 값을 갖습니다. 아래는 위 그래프를 인접행렬로 표현한 것입니다.
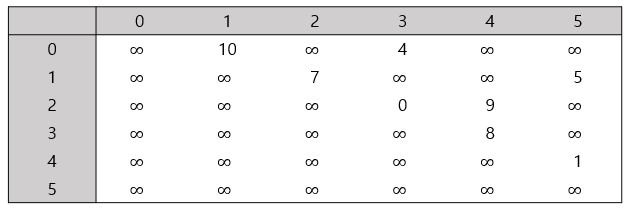
이 인접행렬에서는 연결된 간선이 없을 때는 특수 값으로 \(\infty\)를 사용했지만, 가중치들이 음수가 아니면 -1을 사용할 수도 있고, NULL이나 다른 것을 사용할 수도 있습니다.
인접행렬이 아닌 인접 리스트를 사용할 수도 있습니다. 인접 리스트를 사용하면, 리스트의 각 노드에는 정점이 이름뿐만 아니라 해당 간선의 가중치를 저장해야 합니다.

임계 경로 Critical Path
가중치 그래프를 작업 스케줄링에 초점을 맞추면 위상 정렬은 프로세스에서 수행될 단계들을 표현하는 DAG에서 임계 경로(Critical Path)를 찾는 문제가 됩니다. 이 문제에서 처리할 프로세스는 그래프로 표현되고, 각 노드(정점)은 작업, 링크(간선)는 프로세스 작업 간 순서 관계를 나타냅니다. 여기서 각 간선 \((u, v)\)에서 가중치 \(w(u, v)\)를 할당하는데, 이는 작업 \(v\)를 시작하기 전에 작업 \(u\)를 완료하는데 걸리는 시간입니다.
아래 이미지는 이러한 스케줄링 그래프(scheduling graph)를 보여줍니다.
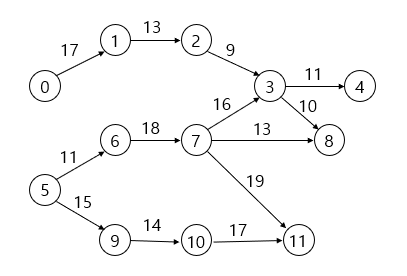
노드는 개별 작업(0부터 코드화된 숫자)에 해당하며, 가중치는 한 작업에서 다른 작업으로 이동하는 데 필요한 시간(예를 들어 주 weak)에 해당합니다. 위 그래프에서 작업 0에서 작업 1까지 도달하는데 17주가 걸립니다.
여기서 발생하는 문제는 프로세스를 완료하는데 필요한 최소 시간이 얼마인가입니다.
일부 작업은 병렬로 수행할 수 있는데, 예를 들어 작업 0과 작업 5의 처리를 동시에 시작할 수 있습니다. 작업 0과 5의 실행이 완료되면 마찬가지로 작업 1, 6, 9 또한 서로를 기다리지 않고 실행할 수 있습니다. 그러나 모든 작업들이 동시에 수행될 수 있는 것은 아닙니다. 작업 3은 작업 2와 7이 완료된 후에 실행될 수 있습니다.
작업을 병렬로 실행할 가능성을 고려할 때 모든 작업을 완료하는데 걸리는 최소 시간은 얼마일까요?
이 답을 찾기 위해서는 다음과 같이 합니다.
먼저 두 개의 노드를 그래프에 추가합니다. 하나는 시작 노드 s이고 전체 프로세스의 시작 지점입니다. 이 노드는 소스 노드(source node)라고 불립니다. 그래프에서 선행 작업이 없는 노드에 각각 s를 연결하며, 추가되는 연결 간선들은 가중치가 0이 됩니다. 다른 하나는 전체 프로세스의 끝을 나타내는 또 다른 노드 t를 추가하는데, 이 노드는 싱크 노드(sink node)라고 합니다. 후속 작업이 없는 노드들을 t에 연결합니다.
이 작업이 끝나면 아래처럼 그래프가 구성됩니다.

소스 노드와 싱크 노드를 추가하고 나면 다음의 문제가 등장합니다.
노드 s에서 노드 t로 가는 가장 긴 경로는 무엇일까요?
그래프의 모든 노드를 방문해야 하므로 s에서 t까지 모든 경로를 거쳐야 합니다.
물론 일부 경로는 병렬로 작업할 수 있지만, 그러나 가장 긴 시간이 걸리는 경로를 완료할 때까지 프로세스를 완료할 수 없습니다.
이처럼 프로세스에서 가장 긴 경로를 임계 경로(Critical Path)라고 합니다.
조금 더 간단한 예를 살펴봅시다.

경로 0 -> 1 -> 2 -> 4의 길이는 16입니다. 경로 0 -> 4의 길이는 14, 경로 0 -> 3 -> 4는 20입니다. 길이 단위가 주라면 20주가 되기 전에 작업 4를 시작할 방법이 없으므로 임계 경로는 0 -> 3 -> 4가 됩니다.
같은 방식으로 위의 그래프에서 s에서 t까지의 가장 긴 경로에 걸리는 시간이 지나서야 프로세스의 마지막인 t를 시작할 수 있습니다. 이때 t는 프로세스의 마지막을 나타내는 자리 표시자일 뿐입니다.
그렇다면 가장 긴 경로는 어떻게 찾을 수 있을까요?
일단 순차적으로 그래프를 탐색해야합니다. 특히, s부터 시작하여 그래프에 있는 모든 노드를 방문하고, s에서 각 노드까지 경로의 길이를 계산합니다. 초기에 알고 있는 유일한 길이는 s까지의 길이인 0입니다.
각 노드들을 방문하면서 길이를 갱신하는데, 노드 \(u\)를 방문해서 s에서 \(u\)까지 가장 긴 경로를 찾았고, \(u\)는 \(v\)와 연결되었다고 가정해봅시다. s부터 \(v\)까지에서 찾은 가장 긴 경로가 s부터 \(u\)까지 경로에 간선 \((u, v)\)의 가중치를 더한 것보다 작거나 같다면, \(v\)까지 발견한 가장 긴 경로는 \(u\)를 지나간다는 정보를 기록하고 계산된 길이를 갱신해야 합니다. (\(u\)를 수행하기 전까지 \(v\)를 수행할 수 없다는 뜻이기 때문입니다.)
이렇게 노드를 탐색하면서 더 긴 경로를 찾을 때마다 길이를 갱신해야 하므로, 시작할 때 s까지의 길이를 제외하고는 모든 길이를 가능한 가장 낮은 추정값(ex, \(-\infty\))으로 설정해야 합니다.
정확한 측정을 통해 그래프 측량에 대한 추정값을 확인하고 필요에 따라 갱신하는 프로세스는 많은 그래프 알고리즘에서 일어나는 일인데, 이를 완화(relaxation)이라고 합니다. 여기에서 경로 길이에 대한 초기 추정값은 가장 작은 값인 \(-\infty\)이며, 경로 길이를 갱신할 때마다 덜 극단적인고 더 정확한 값으로 완화됩니다.
\(v\)로의 경로를 처음 확인할 때 가능한 가장 작은 값인 \(-\infty\)임을 알게 되면 \(u\)에서 전달되는 경로의 길이로 정확히 갱신해야 합니다.
또한, \(v\)로 향하는 모든 노드를 방문하기 전까지 노드 \(v\)를 방문해서 \(v\)의 인접 노드로 방문하면 안됩니다. 이는 앞선 글의 위상 정렬(Topological Sort)로 그래프를 탐색하면 방문 순서를 쉽게 얻을 수 있습니다.
위 내용을 알고리즘으로 나타내면 다음과 같습니다.

이 알고리즘에서는 배열 pred와 배열 dist라는 두 가지 자료 구조를 사용합니다.
(아래에서 확인할 수 있지만, 저는 배열이 아닌 해시테이블을 사용했습니다. 우선 배열이라는 가정 하에 설명하겠습니다.)
pred의 원소 i, 즉, pred[i]는 i에 해당하는 노드까지의 임계 경로에서 i 앞에 오는 노드를 가리킵니다. 즉, i 전에 위치하는 노드입니다. dist의 원소 i, dist[i]는 i에 해당하는 노는까지 임계 경로의 길이를 나타냅니다. 여기서 Weight는 노드 \(u\)와 \(v\) 사이의 가중치를 반환하는 함수입니다. 이 알고리즘에서 입력으로 t는 요구하지 않습니다. 이는 t가 어느 노드인지를 아는 것으로 충분하기 때문이고, 임계 경로의 길이는 dist[t]로 주어지고, 경로를 찾기 위해 pred[t]에서 출발하여 pred를 추적하면 됩니다.
1~6행에서는 pred와 dist 자료 구조를 생성하고 초기화합니다. pred의 각 원소를 유효하지 않으며 존재하지 않는 노드 -1로 설정했는데, 이는 그래프를 어떻게 사용하느냐에 따라 달리질 수 있습니다. 각 노드의 길이인 dist는 각 원소를 시작 노드인 s를 제외하고는 \(-\infty\)로 설정합니다.
그 다음 그래프에서 위상정렬을 수행하여, 위상 순서를 얻습니다.
그리고 8~12행에서 위상 순서에 따라서 모든 노드를 처리합니다. 즉, 차례대로 인접 리스트를 이용해 각 노드와 이웃 노드들에 대해 반복처리 합니다.
10~12행에서는 현재 노드에서 각 이웃 노드로 가는 경로의 길이가 이 지점까지 계산한 이전 노드보다 더 큰지 확인합니다. 더 크다면 현재 노드까지 오는 가장 긴 경로에 있는 이웃의 선행 노드와 경로 길이를 갱신합니다.
이 알고리즘은 꽤 효율적입니다. 위상 정렬은 \(O(|V| + |E|)\) 시간이 걸립니다. 3~5행의 루프는 \(O(|V|)\) 시간이 걸립니다. 그리고 8~12행의 루프는 간선당 한 번씩 11~12행을 수행하고, 각 간선은 한 번 relaxation 됩니다. 이는 전체 루프가 \(O(|E|)\) 시간이 걸린다는 것을 의합니다.
정리하면 전체 알고리즘을 수행하는 데는 \(O(|V| + |E| + |V| + |E|) = O(|V| + |E|)\) 시간이 필요합니다.
실제로 구현해보도록 하겠습니다.
이전 게시글에서 구현한 Directed Graph에서 criticalPath 함수를 구현했습니다.
GitHub - junstar92/DataStructure_Algorithm
Contribute to junstar92/DataStructure_Algorithm development by creating an account on GitHub.
github.com
우선 기존 코드에서 수정된 함수는 다음과 같습니다.
#include <tuple>
template<typename T>
class DirectedGraph {
...
public:
typedef struct arc {
...
int32_t weight;
} ARC;
...
int insertArc(T fromKey, T toKey, int32_t weight = 0);
...
std::tuple<std::map<T, T>, std::map<T, int32_t>> criticalPath(T start);
};가중치를 적용하기 위해서 ARC 구조체에 weight 변수를 추가했고, 간선을 추가하는 메서드 insertArc에 매개 변수로 weight 값을 입력받고, 구조체의 weight에 대입합니다. default로 0이 들어갑니다.
그리고 criticalPath를 구해서, 각 노드의 pred node와 시작 노드 start부터의 거리를 반환하는 메서드 criticalPath 메서드를 추가했습니다. 위 알고리즘에서는 배열을 사용했지만, template으로 숫자가 아닌 다른 타입도 가능할 수 있도록, 해시테이블을 사용하여 배열처럼 사용했습니다. 그리고 익숙하지 않은 tuple을 사용해서 타입이 다른 각각의 결과를 한 번에 반환하도록 했습니다. (이번 기회에 튜플 사용법을 간단하게 익혀봤습니다.. !)
그럼 바로 criticalPath 메서드의 구현을 살펴보겠습니다.
template <typename T>
std::tuple<std::map<T, T>, std::map<T, int32_t>> DirectedGraph<T>::criticalPath(T start)
{
std::map<T, int32_t> pred;
std::map<T, int32_t> dist;
std::map<T, VERTEX*> vertices;
VERTEX* walkVertPtr = this->first;
// dist, pred initiation, set vertex mapping table
while (walkVertPtr) {
dist[walkVertPtr->data] = (1 << 32);
pred[walkVertPtr->data] = -1;
vertices[walkVertPtr->data] = walkVertPtr;
walkVertPtr = walkVertPtr->pNextVertex;
}
dist[start] = 0;
auto sorted = this->topologicalSort_DFS();
for (auto& u : sorted) {
ARC* walkArcPtr = vertices[u]->pArc;
while (walkArcPtr) {
T v = walkArcPtr->destination->data;
if (dist[v] < dist[u] + walkArcPtr->weight) {
dist[v] = dist[u] + walkArcPtr->weight;
pred[v] = u;
}
walkArcPtr = walkArcPtr->pNextArc;
}
}
return { pred, dist };
}구현은 꽤 간단합니다.
4 ~ 16 line에서 pred와 dist를 초기화합니다. pred는 모두 -1로, dist 값은 int형의 최소값으로 초기화됩니다.
여기서 추가로 vertices라는 해시테이블을 사용했는데, 매번 while문으로 해당 인덱스의 정점을 찾아가는 것이 번거롭기 때문에 초기화를 진행하면서 각 정점의 데이터와 매칭되는 정점 포인터를 저장하는 용도로 사용됩니다.
18 line에서 시작 노드인 start의 dist[start]를 0으로 초기화해주고, 위상 정렬을 통해서 탐색할 노드들의 순서를 전달받습니다.
20 line부터 위상 정렬된 순서로 모든 정점들의 인접 정점들을 탐색하면서 거리를 갱신합니다.
만약 도착한 인접 정점 \(v\)의 거리(dist[v])가 해당 정점 \(u\)의 거리에서 \(w(u, v)\)를 합한 값(dist[u] + Weight(u, v)보다 작다면, dist[v]의 값을 갱신하고, pred[v]에 u를 대입합니다.
모든 정점을 돌면서 이 작업을 반복하면 출발 지점 start에서의 모든 정점까지의 거리인 dist와 정점의 이전 노드를 가리키는 pred를 얻을 수 있습니다.
실제로 잘 동작하는지 살펴보겠습니다 !
#include <iostream>
#include <stdio.h>
#include "DirectedGraph.hpp"
int main(void) {
DirectedGraph<int32_t> graph([](const int32_t& a, const int32_t& b) {
if (a > b)
return 1;
else if (a < b)
return -1;
else
return 0;
});
// add vertex(0 ~ 11)
for (int32_t i = 0; i < 12; i++) {
graph.insertVertex(i);
}
// add edge
graph.insertArc(0, 1, 17);
graph.insertArc(1, 2, 13);
graph.insertArc(2, 3, 9);
graph.insertArc(3, 4, 11);
graph.insertArc(3, 8, 10);
graph.insertArc(5, 6, 11);
graph.insertArc(5, 9, 15);
graph.insertArc(6, 7, 18);
graph.insertArc(7, 3, 16);
graph.insertArc(7, 8, 13);
graph.insertArc(7, 11, 19);
graph.insertArc(9, 10, 14);
graph.insertArc(10, 11, 17);
// add start(-1)/end(12) point
graph.insertVertex(-1);
graph.insertVertex(12);
graph.insertArc(-1, 0, 0);
graph.insertArc(-1, 5, 0);
graph.insertArc(4, 12, 0);
graph.insertArc(8, 12, 0);
graph.insertArc(11, 12, 0);
int32_t start = -1, end = 12;
auto ans = graph.criticalPath(start);
auto pred = std::get<0>(ans);
auto dist = std::get<1>(ans);
printf("--------- distance from start ---------\n");
printf("idx : ");
for (int32_t i = 0; i <= end; i++) {
printf("%2d ", i);
}
printf("\ndist : ");
for (int32_t i = 0; i <= end; i++) {
printf("%2d ", dist[i]);
}
printf("\n\n--------- pred node from each node ---------\n");
printf("idx : ");
for (int32_t i = 0; i <= end; i++) {
printf("%2d ", i);
}
printf("\npred : ");
for (int32_t i = 0; i <= end; i++) {
if (pred[i] == -1)
printf("%2c ", 's');
else
printf("%2d ", pred[i]);
}
printf("\n");
return 0;
}각 정점과 간선을 추가하고, 시작 노드를 -1, 도착 노드를 12로 지정하고 criticalPath 메서드를 수행한 결과입니다.

출발 노드부터 도착 노드까지 가장 긴 경로의 길이는 56이며, 이는 pred 결과를 통해서 도착지점 12부터 역추적하면, 임계 경로가 [s -> 5 -> 6 -> 7 -> 3 -> 4 -> 12] 라는 것을 알 수 있습니다.
전체 코드는 아래 깃헙에서 확인할 수 있습니다 !
GitHub - junstar92/DataStructure_Algorithm
Contribute to junstar92/DataStructure_Algorithm development by creating an account on GitHub.
github.com
'Data Structure & Algorithm > 알고리즘' 카테고리의 다른 글
| [그래프] 벨만-포드 알고리즘(Bellman-Ford Algorithm) (0) | 2021.10.10 |
|---|---|
| [그래프] 다익스트라 알고리즘(Dijkstra's algorithm) (0) | 2021.10.07 |
| [그래프] 위상 정렬 Topological Sort (0) | 2021.10.05 |
| [암호] 디피-헬먼 키 교환 (모듈러 거듭제곱) (0) | 2021.09.27 |
| [암호] AES (C++ 구현/private 함수) - 3 (0) | 2021.09.25 |




댓글