References
- 리얼월드 알고리즘
Contents
- 디피-헬먼 키 교환
- 모듈러 거듭제곱
2021.09.23 - [Data Structure & Algorithm/알고리즘] - [암호] AES (Advanced Encryption Standard) - 1
[암호] AES (Advanced Encryption Standard) - 1
References 리얼월드 알고리즘 Contents AES란? AES 암호화/복호화 알고리즘 Key Scheduling C++ 구현 AES (Advanced Encryption Standard) ? 현대 암호 기술은 특정한 수학적 방법을 사용하여 암호문을 생성합니..
junstar92.tistory.com
이전 글에서 암호화 알고리즘인 AES에 대해서 알아봤습니다.
AES는 대칭 암호화(symmetric cipher)의 한 예로, 암호화와 복호화에 같은 암호화 키를 사용합니다. 만약 암호화와 복호화에 다른 키가 사용된다면 이는 비대칭 암호화(asymmetric cipher)라고 합니다.
그렇다면 AES의 모든 보안은 암호화 키에 달려있다는 것을 의미합니다. 즉, 암호화키가 비밀로 있는 한 비밀은 안전하다는 것입니다. 만약 키가 유출된다면 AES는 손상됩니다. 하지만 이는 AES의 결함은 아닙니다. 모든 암호화에는 일종의 키를 사용하고, AES와 다른 좋은 암호의 보안은 키의 보안과 기밀성에 달려있으며, 이는 버그가 아니라 암호 알고리즘의 특성입니다.
네덜란드의 언어학자이자 암호학자인 아우휘스트 케르크호프스(August Kerckhoffs)는 암호 작동 방법이 비밀이 될 필요가 없고 적의 손에 암호 작동 방법이 넘어가도 문제가 되지 않는다고 주장했습니다. 즉, 암호의 모든 비밀은 암호화 방법이 아닌 암호화 키 자체에 의존해야 한다는 것입니다.
암호가 어떻게 작동하는지를 적이 모른다면 그것을 깰 수 없을 것이라는 모호함을 통한 보안(security by obscurity) 개념으로 보안을 유지하는 것을 틀렸습니다. 만약 이것이 최선의 방어라면 적은 최고의 방법으로 암호 시스템이 어떻게 작동하는지 알아낼 것이기 때문입니다. 아니면 적이 누군가를 매수할 수도 있습니다.
그렇지만 키에 대한 보안을 제한하면 키가 비밀로 유지되는 한 비밀을 보장할 수 있고 이는 전체 설계 비밀을 유지하는 것보다 훨씬 쉬운 일입니다.
AES 외에도 다른 대칭 암호화 알고리즘이 있는데, 이들 모두 보안은 키를 숨긴 채 유지하는 데 달려있습니다. 이러한 암호화들은 또한 통신의 당사자 모두가 같은 키에 동의하기를 요구합니다. 하지만 여기서 문제가 있습니다. 누군가에게 보낼 메세지를 암호화하고 싶다면 사용할 키에 어떻게든 동의(전달)해야 합니다. 물리적으로 가까이 있다면 만나서 키를 교환하기만 하면 되므로 쉬울 수 있지만, 그렇지 않다면 단순히 수신인에게 키를 전달할 수는 없습니다. 키가 암호화되지 않았기 때문에 전송 중에 누군가 가로챌 수 있으며 모든 보안이 무용지물이 될 수 있습니다.
디피-헬먼 키 교환
이러한 암호 키 교환 문제를 어떻게 해결하는 지 예시를 통해서 살펴보겠습니다.
통신의 두 당사자인 앨리스(Alice)와 밥(Bob)이 메세지를 암호화하고 복호화하는 데 사용할 키를 교환한다고 가정해봅시다. 키를 교환하기 전에 이들은 일련의 다른 메세지를 주고 받습니다. 이러한 메세지들은 단순한 평문이고 공유하려는 키를 포함하지 않습니다. 그러나 메세지 교환 작업이 끝나면 앨리스와 밥은 같은 키를 공유하게 됩니다. 키는 어느 쪽에서도 직접 보낸 적이 없으므로 누구도 가로챌 수 없었을 것입니다.
이것은 다음의 방법을 통해서 가능하게 됩니다.
앨리스와 밥은 우선 두 수를 선택합니다. 이 두 수는 \(2 \leq g \leq p - 2\) 조건을 만족하는 소수 p와 소수일 필요가 없는 g 입니다.(g의 조건이 이와같은 이유는 아래에서 설명하도록 하겠습니다.)
여기서 수행될 모든 계산은 모듈로 p로 이루어지고, p는 계수(modulus)이고 g는 밑(base)가 됩니다.
만약 앨리스와 밥이 \(p = 23\)과 \(g = 14\)를 선택했다고 합시다. 그리고 이 두 수를 비밀로 할 필요가 없고, 공개적으로 공표해도 무관합니다.
그리고 앨리스는 \(1 \leq a \leq p - 1\)을 만족하는 비밀숫자 a(앨리스만 알고있는)를 선택합니다. 앨리스가 \(a = 3\)을 선택했다면 이 숫자를 다음과 같이 계산합니다.
\[A = g^a \text{ mod } p\ = 14^3 \text{ mod } 23 = 2744 \text{ mod } 23 = 7\]
여기서 계산 결과가 모듈로 p 이므로 앨리스가 \(a \geq p\)를 선택하는 것은 의미가 없습니다.
앨리스가 숫자 A, 즉 7을 밥에게 전송합니다.
이제 밥은 다시 \(1 \leq b \leq p - 1\)을 만족하는 비밀숫자 b(밥만 알고있는)을 선택합니다. 밥이 \(b = 4\)를 선택했다면 앨리스가 비밀숫자 a에 한 것과 같은 연산을 b로 수행합니다.
\[B = g^b \text{ mod } p\ = 14^4 \text{ mod } 23 = 38416 \text{ mod } 23 = 6\]
계산 후, 밥은 숫자 B, 즉 6을 앨리스에게 전송합니다.
각자 전송한 후에 앨리스는 전달받은 숫자 B로 다음 수를 계산합니다.
\[B^a \text{ mod } p = 6^3 \text{ mod } 23 = 216 \text{ mod } 23 = 9\]
밥은 전달받은 A로 다음 수를 계산합니다.
\[A^a \text{ mod } p = 7^4 \text{ mod } 23 = 2401 \text{ mod } 23 = 9\]
앨리스와 밥은 동일한 결과 9를 얻게 되고, 이 숫자 9가 바로 암호화/복호화에 사용될 키가 됩니다.
이처럼 이들은 숫자 9를 전혀 교환하지 않고 계산으로 같은 결과를 얻어서 키로 사용할 수 있습니다. 게다가 앨리스와 밥 사이의 통신을 가로채 비밀을 밝힐 수 있는 방법도 없습니다. 다시 말하자면, p, g, A, B로는 비밀을 알아낼 수 없습니다.
이 키 교환 방법을 디피-헬먼 키 교환(Diffie-Hellman key exchange)이라고 합니다.
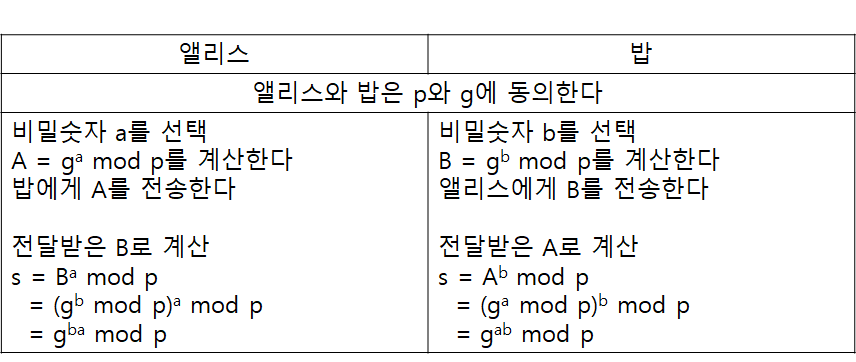
즉, \(g^{ba} \text{ mod } p = g^{ab} \text{ mod } p\) 이므로 앨리스와 밥은 같은 수를 계산하여 키로 사용할 수 있습니다. 이는 아래의 모듈러 산술 법칙으로부터 계산할 수 있습니다.
\((u \text{ mod } n)^k \text{ mod } = u^k \text{ mod } n\) 이므로
\((g^b \text{ mod } p)^a \text{ mod } = g^{ba} \text{ mod } p\)와
\((g_a \text{ mod } p)^b \text{ mod } = g^{ab} \text{ mod } p\)를 구할 수 있습니다.
이 디피-헬먼 키 교환 방법은 앨리스와 밥이 a와 b를 비밀로 하는 한 안전합니다. 또한 키를 교환하고 난 후에는 더 이상 필요없으므로 폐기해도 됩니다.
키 교환의 보안은 다음 문제가 얼마나 어려운가에 달려 있습니다.
즉, 소수 p와 숫자 g 그리고 \(y = g^x \text{ mod } p\)라면 이산 로그 문제는 이 방정식에서 \(1 \leq x \leq p - 1\)을 만족하는 정수 x를 찾는 것입니다. (참조 : ko.wikipedia.org/wiki/이산_로그)
정수 \(x\)는 \(g\)를 밑으로 하는 \(y\)의 이산 로그라고 하고 \(x = log_g y \text{ mod } p\)라고 씁니다.
\(y = g^x \text{ mod } p\)는 일종의 일방향 함수(one-way function)으로 계산하기는 쉽지만, 역을 구하기는 어려운 문제입니다. 따라서 \(g, x, p\)가 주어지면 \(y\)를 계산하기는 쉽지만, \(y, g, p\)가 주어졌을 때 \(x\)를 구하는 효과적인 방법은 모르며, 할 수 있는 것은 정확한 값을 찾을 때까지 \(x\)에 어려 값을 대입해서 시도해보는 것밖에 없습니다.
사실, 하나의 수에 대해서 거듭제곱 수를 증가시키며 증가 값을 생성하는 지수 함수의 동작은 예측할 수 있지만, 거듭제곱 모듈로 소수의 동작은 예측하기 어렵습니다. 아래의 표를 살펴봅시다.

위 표를 보면, 로그를 취함으로써 \(g^x\)로부터 \(x\)를 쉽게 얻을 수 있지만, \(g^x \text{ mod } p\)로부터 로그를 취하거나 또는 다른 알려진 공식을 사용하여 \(x\)를 구할 수는 없습니다.
그리고 정상적인 2의 거듭제곰은 연속적으로 2를 곱함으로써 생성되지만, 2의 거듭제곱 값의 모듈로 13은 명확한 패턴이 없이 1부터 12 사이에 있는 모든 수를 나타냅니다. 저 표 이후로는 같은 사이클을 돌며 진행합니다.
실제로
\(x = 13\)이라면 \(2^{13} \text{ mod } 13 = (2^{12} \times 2) \text{ mod } 13 = ((2^{12} \text{ mod } 13) \times (2 \text{ mod } 13)) \text{ mod } 13 = (1 \times 2) \text{ mod } 13 = 2\)
라는 결과를 얻습니다.
일반적으로
\[2^{12+k} \text{ mod } 13 = ((2^12 \text{ mod } 13) \times (2^k \text{ mod } 13)) \text{ mod } 13 = (1 \times 2^k) \text{ mod } 13 = 2^k \text{ mod } 13\]
이므로, \(2^x \text{ mod } 13\) 함수가 주기적(주기 : 12)이라는 것을 알 수 있습니다.
하지만 이러한 일이 항상 발생하는 것은 아닙니다.

연속한 \(3^x \text{ mod } 13\)을 살펴보면, 모듈러 거듭제곱이 1부터 12까지의 모든 값만 나타내는 것이 아니라 그 부분 집합(3, 9, 1)으로도 나타냅니다. 위 경우에는 기본주기가 3이 됩니다.
연속한 \(g^x \text{ mod } p\)의 값이 1부터 p-1까지의 모든 수를 포함할 때 g를 생성자(generator) 또는 원시 원소(primitive element)라고 합니다. 더 정확히 말하자면 군 생성자(group generator) 또는 군 원시 원소(group primitive element)라고 부릅니다. 이는 p가 소수일 때 숫자 \(1, 2, \cdots, (p-1)\)은 이들을 모듈로 p(modulo p)로 곱할 때 대수와 수 이론에서 중요한 개념인 곱셈군(multiplicative group)을 형성하기 때문입니다.
그래서 생성자로서 g를 선택해야 합니다. 사실 연속한 \(g^x \text{ mod } p\) 값이 숫자 \(1, 2, \cdots, (p-1)\)의 충분히 큰 부분집합이어서 이산 로그 문제에 대한 해법을 찾는 시도가 비실용적이라면 생성자 없이도 충분히 선택할 수 있습니다.
그리고 \(g^x \text{ mod } p\)의 값이 1이 되면 값이 반복되기 시작합니다.
\(g = p - 1\)이면 \(g^1 \text{ mod } p = (p-1) \text{ mod } p = p-1\)이 됩니다.
\((p-1)^2 = p(p-2) + 1\) 이므로 \(g^2 \text{ mod } p = (p-1)^2 \text{ mod } p = 1\) 입니다. 따라서 모든 거듭제곱은 p-1 또는 1이 됩니다.
만약 \(g = 1\)이라면 모든 거듭제곱은 1이 됩니다. 따라서 g를 선택할 때, g의 조건이 \(2 \leq g \leq p - 1\)이어야하는 이유입니다.
다시 디피-헬먼 키 교환으로 돌아가서, 이 키 교환 암호가 해독되지 않음을 보장하려면 \(g^x \text{ mod } p\)에서 \(x\)를 추측할 수 없음을 확실히 해야 하고, 이는 \(p\)가 상당히 큰 수여야 한다는 것을 의미합니다. 예를 들어, 4096 비트로 표현되는 소수 p를 선택할 수 있는데, 이는 p가 최소 1233자리의 10진수입니다.
(이러한 소수를 찾는 방법은 추후에 알아보도록 하겠습니다.)
또한, 적절한 \(g\)를 선택해야 하는데, \(p\)와 달리 생성자를 얻는 데 \(g\)를 큰 값으로 선택할 필요가 없으며, 심지어 2로 선택해도 됩니다.
이렇게 p와 g를 모두 선택하였으면 키 교환을 시작할 수 있게 됩니다. 앨리스와 밥 두 사람이 각자의 비밀숫자 a, b를 선택하고 디피-헬먼 키 교환으로 메세지를 교환하면, AES로 메세지를 암호화하는데 필요한 암호화키를 공유할 수 있게 됩니다. 그리고 원한다면 언제든지 전체 시퀀스를 다시 수행할 수 있으므로 암호화가 끝나면 AES의 암호화키를 버려도 됩니다.
여기서 작은 허점이 존재하는데, 양자 컴퓨터를 위해 고안된 알고리즘은 이산 로그 문제를 다항 시간 내에 해결하므로 양자 컴퓨터가 실용화된다면 다른 암호화 방법뿐만 아니라 디피-헬먼 키 교환이 주는 영향도 큽니다.
모듈러 거듭제곱
디피-헬먼 키 교환은 모듈러 거듭제곱(modular exponentiation)이라는 계산이 필요합니다.
물론 g를 x번 거듭제곱하고 p로 나눈 값의 나머지를 계산하여 \(g^x \text{ mod } p\)를 계산할 수 있지만, 조금만 생각해보면 이는 매우 비효율적입니다. \(g^x\)와 같은 수는 매우 큰 수가 될 수 있지만, 최종 결과는 항상 \(p\)보다 작습니다. 잠재적으로 아주 큰 거듭제곱 수를 계산하지 않고 모듈로 p를 축소하여 식을 계산하는 방법을 찾는다면 좋을 것입니다. 모듈러 산술의 성질을 사용하면 다음을 얻을 수 있습니다.
\[\begin{matrix}
g^2 \text{ mod } p = g \cdot g \text{ mod } p = ((g \text{ mod } p)(g \text { mod }p)) \text{ mod } p\\
g^3 \text{ mod } p = g^2 \cdot g \text{ mod } p = ((g^2 \text{ mod } p)(g \text { mod }p)) \text{ mod } p\\
\cdots \\
g^x \text{ mod } p = g^{x-1} \cdot g \text{ mod } p = ((g^{x-1} \text{ mod } p)(g \text { mod }p)) \text{ mod } p
\end{matrix}\]
이 성질을 이용하여 제곱 모듈로 \(p(g^2 \text{ mod } p)\)로 시작해서 그 결과를 세제곱 모듈로 p를 계산하는데 사용하는 식으로 x차 거듭제곱까지 계속하면 큰 차수의 거듭제곱 모듈로 p의 계산을 효율적으로 할 수 있습니다.
조금 더 효과적인 방법이 있는데, 이 방법이 모듈러 거듭제곱을 계산하는 표준적인 방법입니다.
바로 반복 제곱을 사용한 거듭제곱인데, \(g^x\)를 계산하는 방법을 먼저 살펴보도록 하겠습니다.
먼저 지수를 이진 표기로 작성해보겠습니다. 여기서 각 \(b_i\)는 이진 표기에서 비트 하나에 해당합니다.
\[x = b_{n-1}2^{n-1} + b_{n-2}2^{n-2} + \cdots + b_0 2^0\]
그러면 \(g^x\)를 다음과 같이 계산할 수 있습니다.
\[g^x = g^{b_{n-1}2^{n-1} + b_{n-2}2^{n-2} + \cdots + b_0 2^0}\]
위 식을 정리하면 다음과 같습니다.
\[g^x = (g^{2^{n-1}})^{b_{n-1}} \times (g^{2^{n-2}})^{b_{n-2}} \times \cdots (g^{2^0})^{b_0}\]
이렇게 정리하고 식의 \((g^{2^0})^{b_0}\)부터 시작해서 왼쪽으로 이동하며 계산합니다. 그럼 그 다음은 \((g^{2^1})^{b_1}\), \((g^{2^2})^{b_2}\), \((g^{2^3})^{b_3}\) 등등이 됩니다.
그런데 \((g^{2^0})^{b_0} = g^1 = g\) 이고, \(g^{2^1}\)은 g의 제곱, \(g^{2^2}\)는 \(g^{2^1}\)의 제곱, \(g^{2^3}\)은 \(g^{2^2}\)의 제곱입니다. 즉, \((g^{2^{k-1}})^2 = g^{2 \cdot 2^{k-1}}\) 이므로 이를 일반화하면,
\[g^{2^k} =(g^{2^{k-1}})^2\]
가 됩니다.
이는, 식의 오른쪽에서 왼쪽으로 이동하며 \(i = 1, 2, \cdots, n-1\)에 대해 각 인수에 이전 인수의 밑을 제곱하면 \(g^{2^i}\)를 계산할 수 있다는 것을 의미하며, 이는 아래의 알고리즘으로 나타낼 수 있습니다.

위 알고리즘은 g와 x를 입력 받아 \(g^x\) 값을 출력합니다. 1행에서 밑을 설정하는데, c는 \(g^{2^0}\)에 해당하는 g로 설정하고, 2행에서는 x의 이진 표현을 가져오기 위해 x로 초기화한 변수 d를 설정합니다.
그리고 3행에서는 초기값 1로 설정합니다.
4~8행에서 루프가 x의 이진 표현 비트 수 만큼 실행되며, 5행에서는 d의 최상위비트(가장 오른쪽 비트)가 1이면 계산한 인수 c를 현재 결과에 곱합니다.
7행에서 d를 2로나눈 정수 값을 취합니다. (오른쪽 1비트를 잘라내는 것과 동일하므로, 오른쪽으로 shift하면 됩니다.)
루프의 끝인 8행에서는 c 값을 제곱합니다.
이런 방식으로 거듭제곱을 구하면 지수 x의 이진 표현에 사용된 비트수만큼의 횟수로 g의 거듭제곱을 구할 수 있습니다.
즉, \(O(logx)\) 반복의 복잡도를 갖습니다.
이를 C/C++ 언어로 구현하면 다음과 같이 구현할 수 있습니다.
long long ExpRepeatedSquaring(long long g, long long x)
{
long long c = g;
long long d = x;
long long r = 1;
while (d > 0) {
if (d & 1 == 1) {
r *= c;
}
d >>= 1;
c *= c;
}
return r;
}알고리즘 5행의 mod 2 연산은 실제로 나누기로 계산할 필요가 없습니다. 수의 마지막 비트가 0이면 2로 나누어지고, 그렇지 않으면 나누어지지 않습니다. 따라서 d의 마지막 비트가 0인지를 확인하기만 하면 됩니다. 따라서 AND 비트 연산으로 이를 쉽게 할 수 있습니다. 위 코드의 8행이 이에 해당됩니다.
아래 코드로 테스트해보면 다음의 결과를 얻을 수 있습니다.
int main(void) {
std::cout << ExpRepeatedSquaring(2, 11) << std::endl;
std::cout << ExpRepeatedSquaring(3, 5) << std::endl;
std::cout << ExpRepeatedSquaring(6, 5) << std::endl;
return 0;
}
여기서 문제는 각 반복에 드는 시간인데, 모듈로 연산과 2로 나누는 연산은 단순히 이진 연산을 수행하므로 시간이 오래 걸리지 않습니다. 알고리즘의 6행의 곱셈과 8행의 제곱은 어느 정도 시간이 걸릴 수 있습니다.
제곱은 곱셈보다 두 배 빠르고, 6행보다 8행이 더 많이 반복됩니다. 가장 느린 곱셈을 기준으로 복잡도를 구하면 \(O((\frac{x}{2}\log{g})^2) = O((x\log{g})^2)\)가 됩니다.
알고리즘의 6행보다 8행이 더 많이 반복되고, r은 c보다 더 작으므로 8행만 처리하면 됩니다.
참고로 각각 n비트와 m비트로 된 숫자 a와 b의 곱셈의 복잡도는 \(O(nm)\ = O(\log{a}\log{b})\) 입니다.
첫 번째 반복에서는 g까지의 곱셈(\(g \times g\))이므로 \(O((\log{g})^2)\)의 시간이 필요합니다.
두 번째 반복은 크기 \(g^2\) 곱셈으로 \(O((\log{g}^2)^2) = O((2\log{g})^2)\) 시간이 필요합니다.
마지막 반복은 크기 \(g^{\frac{x}{2}}\) 숫자의 곱셈으로 \(O(\log{g}^{\frac{x}{2}})^2 = O((\frac{x}{2}\log{g})^2)\)의 시간이 필요합니다.
이를 모두 더하면 \(O((2^{i-1}\log{g})^2)\)의 형태를 갖습니다. 전반적으로 복잡도에 영향을 미치는 많은 항이 있지만, 복잡도 함수의 증가는 가장 큰 항에 지배적인 영향을 받으므로 전반적인 복잡도는 \(O((\frac{x}{2}\log{g})^2) = O((x\log{g})^2)\)가 됩니다.
위의 알고리즘 덕분에 이제 모듈러 거듭제곱을 효율적으로 수행할 수 있습니다. 모듈로 연산의 특징 덕분에 c와 r을 계산할 때마다 모듈로를 사용할 수 있고, 아래의 알고리즘으로 구현할 수 있습니다.

C/C++로 구현하면 다음과 같이 구현할 수 있습니다.
long long ModExpRepeatedSquaring(long long g, long long x, long long p)
{
long long c = g % p;
long long d = x;
long long r = 1;
while (d > 0) {
if (d & 1 == 1) {
r = (r * c) % p;
}
d >>= 1;
c = c * c % p;
}
return r;
}
g를 x번 직접 곱하는 반복과 비교해보면, 위 알고리즘이 얼마나 효율적인지 알아볼 수 있습니다.
간단하게 g를 x번 직접 곱하여 모듈로 연산을 하는 함수를 구현해서 걸리는 시간을 비교해보겠습니다.
g = 155, x = 8000, p = 391 인 경우 입니다.
long long SimpleExpRepeatSquaring(long long g, long long x, long long p)
{
long long r = 1;
while (x > 0)
{
r = (r * g) % p;
x--;
}
return r;
}
int main(void) {
printf("------ Simple ExpRepeatSquaring ------\n");
auto t0 = std::chrono::high_resolution_clock::now();
long long result1 = SimpleExpRepeatSquaring(155, 8000, 391);
auto t1 = std::chrono::high_resolution_clock::now();
std::cout << "result : " << result1 << std::endl;
std::cout << "time : " << std::chrono::duration_cast<std::chrono::microseconds>((t1 - t0)).count() << " us\n";
printf("------ ModExpRepeatSquaring ------\n");
t0 = std::chrono::high_resolution_clock::now();
long long result2 = ModExpRepeatedSquaring(155, 8000, 391);
t1 = std::chrono::high_resolution_clock::now();
std::cout << "result : " << result2 << std::endl;
std::cout << "time : " << std::chrono::duration_cast<std::chrono::microseconds>((t1 - t0)).count() << " us\n";
return 0;
}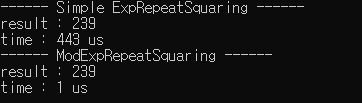
극단적인 결과를 보여주기 위해서 x를 8000으로 설정했는데, 약 400배 이상의 속도를 보여주고 있습니다. 아마 x가 크면 클수록 더욱 큰 차이를 보여줄 것으로 예상합니다.
'Data Structure & Algorithm > 알고리즘' 카테고리의 다른 글
| [그래프] 가중치 그래프와 임계 경로(Critical Path) (0) | 2021.10.06 |
|---|---|
| [그래프] 위상 정렬 Topological Sort (0) | 2021.10.05 |
| [암호] AES (C++ 구현/private 함수) - 3 (0) | 2021.09.25 |
| [암호] AES (C++ 구현/멤버 변수, public 함수) - 2 (0) | 2021.09.23 |
| [암호] AES (Advanced Encryption Standard) - 1 (0) | 2021.09.23 |




댓글