[그래프] 위상 정렬 Topological Sort

References

리얼월드 알고리즘
https://blog.naver.com/kks227/220800013823

Directed Acyclic Graph(DAG)
위상 정렬(Topological Sort)

아래 구현에서 사용되는 그래프 자료구조는 이전 게시글에서 구현한 DirectedGraph 코드를 사용하였습니다. 그래프 자료구조의 구현은 이전 게시글을 참조바랍니다 !

2021.10.04 - [Data Structure & Algorithm/자료구조] - [자료구조] Directed Graph

[자료구조] Directed Graph

References Data Structrue : A Pseudocode Approach with C Contents Graph Directed Graph Graph 그래프는 정점(vertex, vertices)라고 불리는 노드(node)들과 이 정점들을 연결해주는 간선(edge)로 이루어진 자..

junstar92.tistory.com

그래프 자료구조와 전체 코드는 아래에서 확인 가능합니다 !

https://github.com/junstar92/DataStructure_Algorithm/blob/master/Data_Structure/Graph/DirectedGraph.hpp

GitHub - junstar92/DataStructure_Algorithm

Contribute to junstar92/DataStructure_Algorithm development by creating an account on GitHub.

github.com

어떤 작업들이 있을 때, 그 작업이 제한없이 실행되거나 이루어지는 경우는 드뭅니다. 작업들은 서로 관련되어 있을 수 있어서 다른 과제가 먼저 완료되지 않으면 어떤 작업은 시작조차 하지 못할 수 있습니다.

여기서 말하는 작업을 개인적인 일로 바꿔서 이야기해보겠습니다.

전기 주전자로 물을 끓이려면 주전자에 물을 붓고 주전자의 플러그를 콘센트에 연결해야 합니다. 하지만 전기 주전자에 물을 끓이는 일은 토스터를 사용하는 것과 동시에 수행할 수도 있습니다. 그러나 커피를 타기 위해서는 주전자에서 물이 끓기는 기다려야 합니다.

작업 사이에 특정한 의존관계가 있어서 특정 순서로 완료해야하는 것일 수도 있습니다. 예를 들어 학위를 받으려면 일정 수의 과목을 이수해야 하는데, 일부 과목은 선행 과목을 이수해야 하기도 합니다. 이런 경우에 작업은 그 사이에 순서 제한 조건이 있는 일로 생각할 수 있으며, 따라서, 어떤 일은 다른 일보다 선행되어야하고, 다른 작업이 시작되기 전에 완료되어야 합니다.

이러한 작업의 전형적인 예로는 옷을 입는 문제가 있을 수 있습니다. 옷 입기를 생각해보면 정말 많은 단계를 포함하고 있습니다. 속옷, 몇 겹의 옷, 양말, 재킷, 모자 등등이 있습니다. 여기에는 특정 제약이 있어서 겉옷은 속옷을 입기 전에 입을 수 없는 경우가 있을 수 있습니다. 또한, 선택적인 사항도 있는데, 예를 들어 부츠를 먼저 신고 재킷을 입을 수도 있고, 재킷을 입고난 후에 부츠를 신을 수도 있습니다.

다른 예로 캠페인을 생각해보도록 하겠습니다. 사람들에게 무언가를 제안하거나 요청하고 싶을 수 있습니다.

쿠폰이나 기부를 요청할 수 있는데, 사람들의 의사결정에 영향을 미치는 최고의 방법은 다른 사람들이 하는 것, 특히 그들이 알거나 존경하는 사람들이 하는 일을 보여주는 것입니다.

그래서 앨리스가 캠페인에 반응하면, 밥 또한 반응할 것 같다는 것을 미리 알고 있다면 먼저 앨리스에서 접근하고 밥에게 접근하는 것이 좋습니다. 캠페인에서 이러한 관계를 확인하고 인물들을 캐스팅한다고 상상해봅시다.

위 이미지처럼 인물들간의 관계를 나타내는 그래프가 주어져있을 때, 문제는 이 사람들을 어떤 순서로 접촉할 것인가 입니다. 밥과 아이린을 만나기 전에 찰리를 만나고 싶지는 않고, 또한 앨리스를 만나기 전에 밥을 만나고 싶지 않다고 할 수 있습니다. 케네스는 혼자 떨어져 있어서 언제든지 만날 수 있습니다.

이 문제는 결국 방향이 있는 그래프에서 순서를 찾는 것이고, 이에 대한 유일한 정답은 없습니다. 아래 그림처럼 다른 순서로 재배열한 인물들의 캐스팅 그래프(순서)를 볼 수 있습니다.

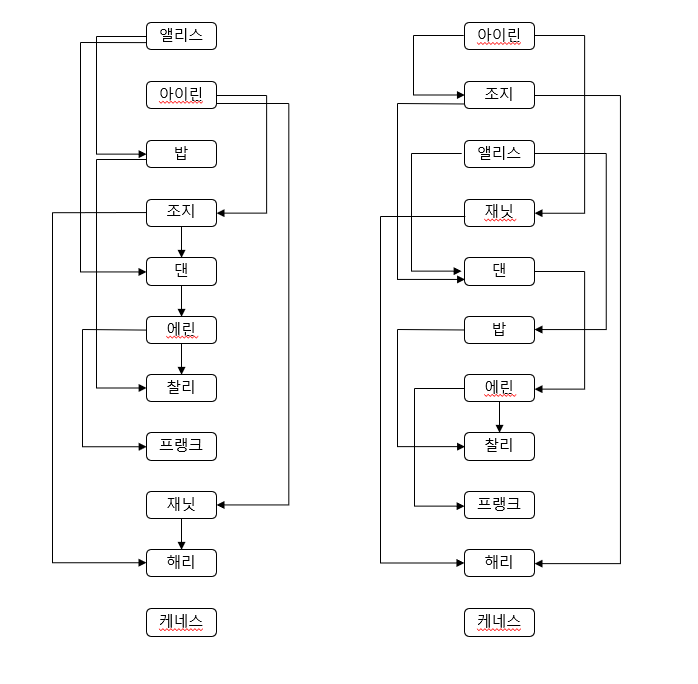
위상 정렬 Topological Sort

위의 인물들의 캐스팅 순서처럼 순서화하는 일반적인 방법을 알아보도록 하겠습니다.

이 문제는 방향이 있는 그래프에서 순서를 찾는 것이라고 했는데, 한 가지 조건이 있습니다.

바로 그래프에서 cycle이 없어야 하는 것인데, 이러한 그래프를 Directed Acyclic Graph(DAG), 방향 비순환 그래프라고 합니다.

즉, 위상 정렬을 하기 위해서는 DAG를 만족해야 합니다.

위의 캐스팅을 위한 그래프에서 앨리스 -> 밥 -> 찰리 순서로 만나야하는데, 만약 찰리에서 앨리스로 이어지는 간선이 있다면 교착상태에 빠지게 되고, 사이클이 생기기 때문에 DAG를 위반하게 됩니다. 따라서 DAG를 만족하지 않는 그래프에서 위상정렬은 의미가 없으며, 반대로 위상정렬을 적용하려면 그래프가 DAG를 만족해야 합니다.

다시 위 캐스팅 예제에서 위상정렬로 돌아가봅시다. 이 그래프에서 위상정렬을 한다고 했을 때, 위상 정렬은 이미 앞에 있는 사람들에게 연락했을 때만 뒤의 누군가에게 연락하는 데 사용할 수 있는 사람들의 순서입니다.

반대로 생각해보면 더욱 쉽습니다. 어떤 사람에게 마지막으로 연락할 것인지를 생각해봅시다.

당연히 누구도 앞에 있지 않은 사람에게 마지막으로 연락할 것이고, 이 예에서는 찰리, 프랭크, 해리, 케네스가 마지막으로 연락할 후보가 됩니다.

마지막으로 연락할 사람을 찾았으면, 이 사람 전에 누구에게 연락할 것인지를 다시 생각해보면 됩니다. 이것 또한, 앞에 누구도 없는 사람을 선택하면 됩니다.

마지막 사람으로 프랭크를 선택했다면 이제 찰리, 해리, 케네스 중에 선택할 수 있습니다. 만약 찰리를 선택한다고 해보면, 마지막으로 프랭크에게 연락하고 프랭크 전에 찰리에게 연락할 것입니다.

찰리에게 연락하기 전에는 누구에게 연락을 해야 할까요? 해리와 케네스 중에서 선택할 수도 있지만, 밥이 찰리 앞에 연결되기 때문에 밥 또한 가능합니다.

이렇게 마지막 사람부터 역방향으로 연락할 사람을 선택하는 방식은 깊이 우선 탐색(DFS)으로 그래프를 탐색하는 것과 같습니다. 시작 지점으로부터 가장 깊은 곳에 있는 노드로 가서 시작 지점까지 역으로 이동합니다. 실제로 DAG에서 DFS를 적용하면 그래프의 위상 정렬 결과를 만들 수 있습니다.

DFS만으로 위상정렬을 할 수 있는 것은 아닙니다.

큐를 사용해서 들어오는 간선이 없는 정점들을 큐에 저장하면서 정렬하는 방법도 있는데, 이는 밑에서 다시 설명하겠습니다.

DFS를 이용한 위상 정렬

그래프를 DFS로 찾아들어가면서 막다른 위치에 도달하여 되돌아가야 할 때 각 원소를 리스트에 추가하면서 정렬을 수행합니다. 이때 추가되는 원소는 리스트의 제일 앞에 추가합니다. 막다른 위치에 도달한 원소가 위상 정렬에서 가장 나중에 도착해야하는 원소이기 때문입니다.

DFS를 사용한 위상정렬을 구현하기 위해서 DirectedGraph 클래스에 두 개의 메서드를 추가했습니다.

template <typename T>
class DirectedGraph
{
private:
	...
    void _topologicalSort_DFS(cosnt VERTEX* curVertex, std::map<T, bool>& visited, std::list<T>& sorted);
	    
public:
	...
    std::list<T> topologicalSort_DFS();
}

먼저 _topologicalSort_DFS 메서드 먼저 살펴보겠습니다.

3개의 파라미터를 입력받습니다. curVertex는 현재 정점 노드이고, visited는 각 정점의 방문 여부를 저장하는 해시테이블입니다. 그리고 sorted는 위상정렬된 결과를 저장하는 리스트 자료구조입니다.

template <typename T>
void DirectedGraph<T>::_topologicalSort_DFS(const VERTEX* curVertex, std::map<T, bool>& visited, std::list<T>& sorted)
{
	visited[curVertex->data] = true;

	const ARC* walkArcPtr = curVertex->pArc;
	while (walkArcPtr) {
		if (!visited[walkArcPtr->destination->data]) {
			this->_topologicalSort_DFS(walkArcPtr->destination, visited, sorted);
		}
		walkArcPtr = walkArcPtr->pNextArc;
	}

	sorted.push_front(curVertex->data);
}

알고리즘은 간단합니다.

현재 방문한 정점 노드의 visited 값을 true로 설정해준 뒤(line 4), 해당 정점에서 나가는 간선들을 탐색합니다(line 6 ~).

탐색된 간선의 도착지가 이전에 방문하지 않았다면, 그 정점으로 _topologicalSort_DFS를 호출합니다(line 9).

그리고 DFS를 진행하면서 막다른 위치에 도달하게 되면 해당 정점을 리스트의 제일 앞에 추가합니다(line 14).

그리고 topologicalSort_DFS 메서드를 통해 초기 환경 설정을 해주고, 위 알고리즘을 사용하여 위상 정렬을 수행할 수 있습니다.

template <typename T>
std::list<T> DirectedGraph<T>::topologicalSort_DFS()
{
	std::map<T, bool> visited;
	
	const VERTEX* walkPtr = this->first;
	while (walkPtr) {	// visited initiation
		visited[walkPtr->data] = false;
		walkPtr = walkPtr->pNextVertex;
	}

	std::list<T> sorted;
	walkPtr = this->first;
	while (walkPtr) {
		if (!visited[walkPtr->data])
			this->_topologicalSort_DFS(walkPtr, visited, sorted);
		walkPtr = walkPtr->pNextVertex;
	}

	return sorted;
}

line 4 ~ 10에서 모든 정점의 visited를 false로 초기화해주고, line 12에서 위상정렬 결과를 저장할 리스트 sorted를 만들어줍니다.

그 다음 모든 정점을 방문할 때까지 탐색하면서 _topologicalSort_DFS 메서드를 호출합니다(line 13 ~ 18). 만약 첫 번째 노드부터 모든 노드를 방문할 수 있다면, 첫 번째 _topologicalSort_DFS 메서드 호출에서 모든 정렬이 끝나게 됩니다.

알고리즘의 동작을 살펴보겠습니다.

우선 모든 정점이 이름순으로 정렬되어 있기 때문에, 위의 캐스팅 그래프를 이름을 순서 인덱스로 변경하면 아래처럼 됩니다. 0 = 댄, 1 = 밥, 2 = 아이린, ..., 9 = 프랭크, 10 = 해리가 됩니다. 이 이름 순서로 topologicalSort_DFS에서 탐색하게 됩니다.

위상정렬을 수행하면, 아래 박스 오른쪽 위에 순서대로 탐색을 수행하게 됩니다.

그리고 막다른 위치에 도달했을 때 리스트의 처음에 원소를 삽입하기 때문에 삽입된 원소 순서의 역순입니다.

따라서, (찰리 <- 프랭크 <- 에린 <- 댄 <- 밥 <- 해리 <- 재닛 <- 조지 <- 아이린 <- 앨리스 <- 케네스), 이 순서로 위상 정렬이 수행됩니다.

#include <iostream>
#include <string>

#include "DirectedGraph.hpp"

int compare(const std::string& str1, const std::string& str2) {
	if (str1 > str2)
		return 1;
	else if (str1 < str2)
		return -1;
	else
		return 0;
}

void printSorted(std::list<std::string> sorted) {
	for (auto& str : sorted) {
		std::cout << str;
		if (sorted.back() != str) {
			std::cout << " -> ";
		}
		else {
			std::cout << "\n";
		}
	}
}

int main(void) {
	DirectedGraph<std::string> graph(compare);

	graph.insertVertex("앨리스");
	graph.insertVertex("아이린");
	graph.insertVertex("밥");
	graph.insertVertex("찰리");
	graph.insertVertex("댄");
	graph.insertVertex("에린");
	graph.insertVertex("프랭크");
	graph.insertVertex("조지");
	graph.insertVertex("해리");
	graph.insertVertex("재닛");
	graph.insertVertex("케네스");

	graph.insertArc("앨리스", "밥");
	graph.insertArc("앨리스", "댄");
	graph.insertArc("밥", "찰리");
	graph.insertArc("댄", "에린");
	graph.insertArc("에린", "찰리");
	graph.insertArc("에린", "프랭크");
	graph.insertArc("조지", "댄");
	graph.insertArc("조지", "해리");
	graph.insertArc("아이린", "조지");
	graph.insertArc("아이린", "재닛");
	graph.insertArc("재닛", "해리");

	graph.printVertex();
	std::cout << "\n\n";
	auto sorted1 = graph.topologicalSort_DFS();
	printSorted(sorted1);

	return 0;
}

Queue를 사용한 위상정렬

큐를 사용한 위상정렬도 간단합니다.

알고리즘은 다음 순서로 진행됩니다.

먼저, 해당 정점으로 들어오는 간선이 없는 (indegree가 0인)정점을 모두 큐에 삽입합니다.

그리고, 큐에서 하나씩 빼면서 나가는 간선들을 체크하면서 해당 간선의 도착 정점의 indegree 값을 1씩 감소시킵니다. 감소하면서 indegree가 0이 된 간선을 큐에 추가합니다. 이 작업을 그래프의 정점 개수만큼 반복합니다.

이때, 이 알고리즘에서 큐에서 빼는 순서가 바로 위상 정렬의 결과가 됩니다.

알고리즘을 수행하는 topologicalSort_Q 메서드 입니다.

template <typename T>
class DirectedGraph {
	...
public:
	...
	std::list<T> topologicalSort_Q();
}

template <typename T>
std::list<T> DirectedGraph<T>::topologicalSort_Q()
{
	std::map<T, uint32_t> inDegrees;
	std::queue<const VERTEX*> q;

	const VERTEX* walkPtr = this->first;
	while (walkPtr) {	// inDegrees initiation
		inDegrees[walkPtr->data] = walkPtr->inDegree;

		if (walkPtr->inDegree == 0)
			q.push(walkPtr);

		walkPtr = walkPtr->pNextVertex;
	}

	std::list<T> sorted;
	for (int i = 0; i < this->count; i++) {
		if (q.empty()) {
			std::cout << "Failed to sort\n";
			sorted.clear();
			return sorted;
		}

		const VERTEX* curPtr = q.front();
		q.pop();
		sorted.push_back(curPtr->data);

		const ARC* walkArcPtr = curPtr->pArc;
		while (walkArcPtr) {	// search adj vertex
			inDegrees[walkArcPtr->destination->data]--;
			if (inDegrees[walkArcPtr->destination->data] == 0)
				q.push(walkArcPtr->destination);

			walkArcPtr = walkArcPtr->pNextArc;
		}
	}

	return sorted;
}

여기서 inDegrees는 각 정점의 indegree 값을 저장하는 해시테이블입니다. 반복 수행하면서 indegree 값을 감소시켜야하기 때문에 따로 해시테이블을 생성하여 값을 저장하도록 했습니다(line 4 ~ 15). 초기화하면서 indegree가 0인 정점들을 큐에 삽입해둡니다.

그리고 정점의 개수만큼 반복하면서 큐에서 빼내며 작업을 수행합니다. 여기서 큐에서 빼는 순서가 위상 정렬의 순서이므로 빼는 것과 동시에 sorted 리스트의 뒤에 원소를 삽입합니다. (DFS와는 반대로 처음이 아닌 마지막에 추가하게 됩니다.)

큐를 사용하면 방문하는 순서는 다음과 같습니다.

#include <iostream>
#include <string>

#include "DirectedGraph.hpp"

int compare(const std::string& str1, const std::string& str2) {
	if (str1 > str2)
		return 1;
	else if (str1 < str2)
		return -1;
	else
		return 0;
}

void printSorted(std::list<std::string> sorted) {
	for (auto& str : sorted) {
		std::cout << str;
		if (sorted.back() != str) {
			std::cout << " -> ";
		}
		else {
			std::cout << "\n";
		}
	}
}

int main(void) {
	DirectedGraph<std::string> graph(compare);

	graph.insertVertex("앨리스");
	graph.insertVertex("아이린");
	graph.insertVertex("밥");
	graph.insertVertex("찰리");
	graph.insertVertex("댄");
	graph.insertVertex("에린");
	graph.insertVertex("프랭크");
	graph.insertVertex("조지");
	graph.insertVertex("해리");
	graph.insertVertex("재닛");
	graph.insertVertex("케네스");

	graph.insertArc("앨리스", "밥");
	graph.insertArc("앨리스", "댄");
	graph.insertArc("밥", "찰리");
	graph.insertArc("댄", "에린");
	graph.insertArc("에린", "찰리");
	graph.insertArc("에린", "프랭크");
	graph.insertArc("조지", "댄");
	graph.insertArc("조지", "해리");
	graph.insertArc("아이린", "조지");
	graph.insertArc("아이린", "재닛");
	graph.insertArc("재닛", "해리");

	graph.printVertex();
	std::cout << "\n\n";
	auto sorted2 = graph.topologicalSort_Q();
	printSorted(sorted2);

	return 0;
}

위에서는 캐스팅 그래프가 DAG라는 가정하에 위상정렬을 수행했습니다.

그렇다면 만약 아래처럼 DAG가 아니라면 어떻게 될까요?

위처럼 찰리에서 앨리스로 간선이 존재하게 된다면, 위상정렬은 의미가 없습니다. 앨리스와 찰리 중에 누구에게 먼저 연락해야할 지 알 방법이 없기 때문입니다. 따라서 위상정렬 전에 DAG를 만족하는 지 체크하는 것이 필요할 수 있습니다.

(DAG를 만족하는 지 확인하는 방법은 추후에 업데이트하도록 하겠습니다.)

위상정렬은 어떤 작업을 어떤 순서로 할 것인지를 찾는 문제에서 활용할 수 있습니다. 여기서는 사람을 연결하는 예시를 활용했지만, 작업은 무엇이든 될 수 있습니다. 예를 들어, 프로세스가 다른 것들보다 선행되어야 하는 제약 조건에 따라 수행되어야 할 수도 있고, 어떤 책들은 각 장의 접근 순서를 기술한 탐색 맵을 도입부에 넣기도 합니다. 용어집은 알파벳 순으로 정렬할 수 있고, 용어 정의에 속한 용어들이 먼저 나오는 방식으로 정렬할 수도 있습니다.

'Data Structure & Algorithm > 알고리즘' 카테고리의 다른 글

[그래프] 다익스트라 알고리즘(Dijkstra's algorithm) (0)	2021.10.07
[그래프] 가중치 그래프와 임계 경로(Critical Path) (0)	2021.10.06
[암호] 디피-헬먼 키 교환 (모듈러 거듭제곱) (0)	2021.09.27
[암호] AES (C++ 구현/private 함수) - 3 (0)	2021.09.25
[암호] AES (C++ 구현/멤버 변수, public 함수) - 2 (0)	2021.09.23

별준

[그래프] 위상 정렬 Topological Sort

References

Contents

위상 정렬 Topological Sort

DFS를 이용한 위상 정렬

Queue를 사용한 위상정렬

'Data Structure & Algorithm > 알고리즘' 카테고리의 다른 글

댓글

티스토리툴바

[그래프] 위상 정렬 Topological Sort

References

Contents

위상 정렬 Topological Sort

DFS를 이용한 위상 정렬

Queue를 사용한 위상정렬

'Data Structure & Algorithm > 알고리즘' 카테고리의 다른 글

관련글

댓글

티스토리툴바