References
- Data Structrue : A Pseudocode Approach with C
Contents
- Graph
- Directed Graph
Graph
그래프는 정점(vertex, vertices)라고 불리는 노드(node)들과 이 정점들을 연결해주는 간선(edge)로 이루어진 자료구조입니다. 아래 그림에서 A, B, ..., E, F에 해당하는 것들을 정점(vertex)라고 부르고, 이 vertex 사이의 선을 간선(edge)라고 합니다.
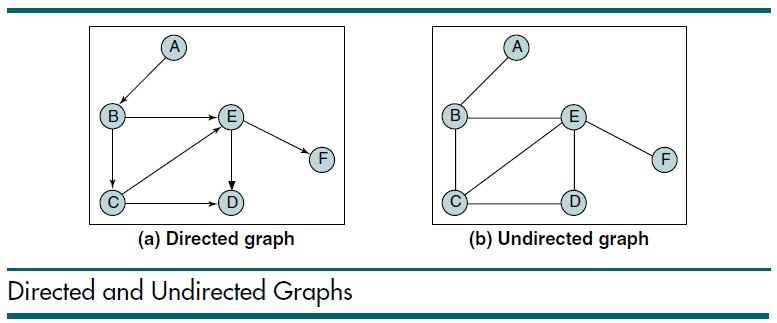
그리고 그래프는 여러 종류가 있지만, 위 그림처럼 크게 directed graph, 방향을 가지는 그래프와 undirected graph, 방향을 가지지 않는 그래프로 분류할 수 있습니다.
즉, 간선(edge)가 방향을 가지느냐 가지지 않느냐로 나누어 지는데, 간선이 방향을 가지게 되면 화살표 방향으로 우선순위(?)를 가지게 된다고 할 수 있습니다. 따라서, 위 (a) 그림에서 정점 A에서는 정점 B로만 이동할 수 있습니다.
반대로 방향을 가지지 않는다면, 두 정점이 연결만 되어 있다면, 어느 점에서나 이어진 정점으로 방문할 수 있습니다. 위 (b) 그림이 undirected graph인데, 이 경우에는 정점 A와 B가 방향이 없는 간선으로 연결되어 있어서 (a)와는 달리 B에서 A로 방문할 수도 있습니다.
여기서 연결된 두 정점 A, B는 인접한 정점(adjacent vertices) 또는 서로 이웃(neighbors)이라고 표현합니다.
이번 글에서는 방향이 있는 그래프인 directed graph에 대해서 실제로 구현해보도록 하겠습니다.
구현하기 전에 추가로 알아둘 용어들이 있습니다.
먼저 경로(path) 입니다.
경로는 인접한 정점들의 시퀀스(sequence)를 의미합니다.

방향이 존재하는 그래프(a)인 경우에는 {A, B, C, D}, {A, B, E, F} 등의 경로가 될 수 있습니다.
만약 방향이 존재하지 않는다면, {A, B, C, D}, {A, B, E, F} 뿐만아니라 {D, E, C, B, A} 등도 있을 수 있습니다.
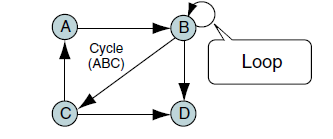
다음은 순환(cycle) 입니다. 순환은 출발 정점과 도착 정점이 동일한 경로를 의미합니다.
위의 (b) 그래프에서 {B, C, D, E, B}가 사이클에 해당됩니다. (a) 그래프에서는 사이클이 존재하지 않습니다.
그리고 하나의 정점이 출발이자 도착지점인 특별한 경우가 있는데, 이는 loop라고 부릅니다.
마지막으로 두 정점 사이에 경로가 존재한다면 그 두 정점은 연결(connected)되었다고 합니다.
그리고 방향이 있는 그래프(directed graph)에서 연결상태에 따라서 3가지로 분류할 수 있는데, weakly connected / strongly connected / disjoint graph로 분류할 수 있습니다.

weakly connected는 적어도 두 개의 정점이 서로 연결되지 않은 그래프를 의미합니다. (a) 그래프
strongly connected는 모든 정점들이 다른 정점들과 경로를 이루는 그래프를 의미합니다. (b) 그래프
disjoint graph는 연결되지 않은 그래프가 있을 때를 의미합니다. 위 이미지의 (c)를 보면, 분리된 그래프가 존재하는 것을 볼 수 있습니다.
마지막으로 degree(차수) 입니다. 차수는 어느 정점에 연결되어 있는 간선의 개수를 의미합니다.

위 그래프에서 B 정점의 차수는 3인데, 총 3개의 간선(A->B,B->C, B->E)가 있습니다.
그리고 차수에서도 outdegree와 indegree로 분리되는데,
outdegree는 해당 정점에서 나가는 간선의 개수이고, 여기서는 (B->C, B->E), 총 2개의 간선이 있습니다.
indgree는 해당 정점으로 들어오는 간선의 개수이고, (A->B), 1개의 간선이 있습니다.
구현
그래프를 표현하기 위해서, 먼저 우리는 두 종류의 데이터를 저장할 공간이 필요합니다.
그래프의 정점을 나타내는 데이터와 그래프의 간선을 나타내는 데이터를 저장해야하는데, 주로 사용되는 방법은 배열(array)을 사용하거나 연결리스트(linked list)를 사용합니다.
Adjacency Matrix 인접 매트릭스
2차원 배열을 사용해서 그래프를 나타내는 방법을 adjacency matrix(인접 매트릭스)라고 합니다.

위 처럼 그래프를 2차원 배열로 나타낼 수 있습니다. 각 행과 열은 그래프의 정점을 나타내고, 2차원 배열의 값이 간선의 상태를 나타냅니다. 만약 값이 0이라면 그 정점들은 연결되지 않았다는 것이고, 1이라면 두 정점이 연결되었다는 것을 의미합니다.
따라서, 방향이 있는 그래프(b)에서 B에서 C로 간선이 연결되어 있다면, 매트릭스 B행C열의 값은 1이 됩니다. 반대로 C에서 B로는 간선이 연결되어 있지 않으므로, C행B열의 값은 0입니다. 방향이 없는 그래프였다면, C행B열의 값도 B행C열과 동일하게 1이 될 것입니다.
Adjacency List 인접 리스트

각 정점과 간선들의 정보를 리스트 구조로 저장하는 방식입니다.
정점들을 저장하는 Vertex list는 singly linked list 방식으로 구현되어 있지만, 방법에 따라서 doubly linked list나 circularly linked list로 구현할 수도 있습니다. 그리고 각 정점에서 오른쪽 포인터는 해당 정점으로부터 나가는 간선들을 의미합니다. B 정점을 살펴보면, B에서 A, C, E로 나가는 간선이 있다는 의미이고 여러 개의 간선이 있을 수 있으므로, 연결 리스트로 B 정점에서 나가는 간선을 모두 표현하고 있습니다.
두 가지 구조 중에서 아마 배열로 구현하는 방법은 인터넷에 찾아보시면 많기 때문에 저는 연결 리스트를 사용해서 그래프를 구현해보도록 하겠습니다.
그래프 자료구조를 구현할 때 먼저 정점과 간선을 어떻게 나타낼 지 고민해야 합니다.

위와 같이 디자인할 수 있는데, 그래프의 정점을 나타내는 구조체(graphVertex)는 data와 indegree/outdegree 정보를 담고 있고, 정점들을 연결 리스트로 연결하기 위해서 다음 정점의 포인터 주소와 해당 정점에서 연결되는 간선들의 정보를 담기 위해서 연결된 간선의 정보를 담고 있는 포인터 주소(firstArc)를 가지고 있습니다.(processed는 사용하지 않을 예정입니다.)
그리고 간선을 나타내는 구조체(graphArc)는 해당 간선의 도착지(destination)과 해당 정점에서 연결되는 또 다른 간선의 정보의 포인터 주소(nextArc)를 가지고 있게 됩니다.
여기서 arc는 방향을 가지는 간선(edge)를 의미합니다. (arc = directed edge)
두 데이터 구조를 코드로 나타내면 다음과 같이 구현할 수 있습니다. 여기서 data는 자료형이 T인데 템플릿으로 어떠한 자료형을 받을 지 결정하도록 할 예정입니다.
typedef struct vertex {
struct vertex* pNextVertex;
T data;
uint32_t inDegree;
uint32_t outDegree;
struct arc* pArc;
vertex() : pNextVertex(nullptr), inDegree(0), outDegree(0), pArc(nullptr) {}
} VERTEX;
typedef struct arc {
struct vertex* destination;
struct arc* pNextArc;
} ARC;Directed Graph 클래스
이제 그래프를 나타내기 위한 데이터 구조체들을 살펴봤으니, 그래프 자료구조가 어떻게 클래스로 구성되는지 살펴보겠습니다.
template <typename T>
class DirectedGraph {
public:
typedef struct vertex {
struct vertex* pNextVertex;
T data;
uint32_t inDegree;
uint32_t outDegree;
struct arc* pArc;
vertex() : pNextVertex(nullptr), inDegree(0), outDegree(0), pArc(nullptr) {}
} VERTEX;
typedef struct arc {
struct vertex* destination;
struct arc* pNextArc;
} ARC;
private:
uint32_t count;
VERTEX* first;
std::function<int(T, T)> compare;
public:
DirectedGraph(std::function<int(const T&, const T&)> func) : count(0), first(nullptr), compare(func) {};
~DirectedGraph();
void insertVertex(T data);
int deleteVertex(T delKey);
int insertArc(T fromKey, T toKey);
int deleteArc(T fromKey, T toKey);
int graphCount() const {
return this->count;
}
void printVertex() const;
};멤버 변수로 정점의 개수를 나타내는 count와 연결리스트로 연결된 정점들의 head를 의미하는 VERTEX 포인터 주소인 first를 가지고 있습니다. 또한, 정점들을 나타내는 연결리스트와 간선들의 연결리스트를 정렬해서 보관하기 위해서 각 데이터를 비교하기 위한 compare 함수 객체도 있습니다. 이 compare 함수 객체의 사용은 밑에서 자세히 살펴보도록 하겠습니다.
멤버 함수는 크게 정점을 추가, 삭제하는 메서드와 간선을 추가, 삭제하는 메서드로 구성되어 있습니다.
insertVertex
template <typename T>
void DirectedGraph<T>::insertVertex(T data)
{
VERTEX* newPtr;
VERTEX* locPtr;
VERTEX* predPtr;
newPtr = new VERTEX();
if (newPtr) {
newPtr->pNextVertex = nullptr;
newPtr->data = data;
newPtr->inDegree = 0;
newPtr->outDegree = 0;
newPtr->pArc = nullptr;
this->count++;
}
else {
printf("Overflow Error 100\a\n");
exit(100);
}
locPtr = this->first;
if (!locPtr) { // if there is no vertex, first is this vertex
this->first = newPtr;
}
else { // else, find insert point
predPtr = nullptr;
while (locPtr && (this->compare(newPtr->data, locPtr->data) > 0)) {
predPtr = locPtr;
locPtr = locPtr->pNextVertex;
}
if (!predPtr) {
this->first = newPtr;
}
else {
predPtr->pNextVertex = newPtr;
}
newPtr->pNextVertex = locPtr;
}
}구현은 간단합니다.
먼저 새로 추가될 vertex의 메모리를 할당하고, 할당 성공 여부를 체크합니다. (line 8 ~ 21)
그리고 정점들의 연결 리스트에 추가하는데, 다른 정점이 존재하지 않는다면 first에 바로 새로 생성한 포인터의 주소를 대입해주고(line 22 ~ 26), 그렇지 않다면 생성한 vertex 포인터를 어디에 추가할 지 탐색을 시작합니다 (line 27 ~).
여기서 compare 함수 객체가 사용되는데, compare의 반환 값에 따라서 어떻게 정렬될 지가 결정됩니다.
std::function<int(T, T)> compare;compare 함수는 파라미터로 두 개의 T 자료형의 데이터를 입력받아서 이 값을 비교하여 int형의 값을 반환하는데, 내부적으로 1, 0, -1을 반환하도록 합니다. (사실 양수, 0, 음수면 됩니다. 굳이 1, -1일 필요는 없음)
예를 들어 compare 함수로 아래와 같은 함수를 사용할 수 있습니다. 여기서 T 자료형은 std::string이 되겠죠.
int compare(const std::string& str1, const std::string& str2) {
if (str1 > str2)
return 1;
else if (str1 < str2)
return -1;
else
return 0;
}저는 여기서 오름차순으로 정렬하기 위해서 str1이 str2보다 먼저 나올 수 있도록 str1 < str2인 경우 -1을 리턴하도록 하였습니다. 이 함수는 algorithm 헤더의 sort 함수의 compare 함수를 정의하는 것과 유사합니다.
따라서, 다시 insertVertex 함수의 while문 내부 조건을 살펴보면,
predPtr = nullptr;
while (locPtr && (this->compare(newPtr->data, locPtr->data) > 0)) {
predPtr = locPtr;
locPtr = locPtr->pNextVertex;
}새롭게 추가되는 정점의 data가 현재 비교할 정점의 data보다 우선순위가 낮을 경우에 while문을 반복하게 되므로, 반복하면서 추가될 위치를 찾게 됩니다.
만약 조건에 맞는 위치를 찾았다면(즉, -1이 리턴됬다면), 현재 위치(locPtr)의 이전 위치(predPtr)의 다음 정점에 새로 추가 될 포인터 주소를 대입해주고, 새로 추가된 포인터의 다음 포인터(pNextVertex)에 현재 위치(locPtr) 주소를 대입해줍니다. 즉, predPtr->locPtr의 순서로 저장되어 있던 정점이 predPtr->newPtr->locPtr의 순서로 newPtr이 추가되는 것입니다.
deleteVertex
template <typename T>
int DirectedGraph<T>::deleteVertex(T delKey)
{
VERTEX* predPtr;
VERTEX* walkPtr;
if (!this->first)
return -2;
predPtr = nullptr;
walkPtr = this->first;
// find delKey
while (walkPtr && (this->compare(delKey, walkPtr->data) > 0)) {
predPtr = walkPtr;
walkPtr->pNextVertex;
}
if (!walkPtr || (this->compare(delKey, walkPtr->data) != 0)) {
return -2;
}
// if vertex has arc, failed to delete
if ((walkPtr->inDegree > 0) || (walkPtr->outDegree > 0))
return -1;
if (!predPtr) {
this->first = walkPtr->pNextVertex;
}
else {
predPtr->pNextVertex = walkPtr->pNextVertex;
}
this->count--;
delete walkPtr;
return 1;
}정점의 data 값으로 해당 정점을 삭제하는 메서드입니다.
간단하게 설명하면, 해당 정점의 위치를 찾아서 해당 정점의 포인터의 메모리를 해제하는 역할을 합니다.
물론 원래 아무 정점도 가지고 있지 않았다면, -2를 리턴하면서 삭제에 실패합니다(line 7 ~ 8).
정점이 존재한다면, walkPtr과 predPtr을 가지고 해당 data를 가진 정점을 탐색하기 시작합니다(line 10 ~ 17).
정점의 연결 리스트는 오름차순으로 정렬되어 있기 때문에, 삭제하고자 하는 데이터의 값이 현재 위치의 데이터보다 우선순위가 낮다면 계속해서 while문을 반복하면서 찾아가게 됩니다.
그렇게 찾은 현재 위치의 데이터 값이 삭제하고자하는 데이터의 값과 같다면 삭제를 진행하고, 그렇지 않다면 -2를 리턴하면서 삭제는 실패하게 됩니다(line 19 ~ 21).
데이터는 일치하지만, 해당 정점에서 뻗어 나가거나 해당 정점으로 들어오는 간선이 존재한다면, 이 경우에도 삭제는 실패하도록 되어 있습니다(line 23 ~ 25). 이 경우에는 삭제하고자 하는 정점의 간선들을 먼저 삭제해주어야 합니다.
모든 조건을 만족하면, 삭제를 진행합니다(line 27 ~ 32).
insertArc
template <typename T>
int DirectedGraph<T>::insertArc(T fromKey, T toKey)
{
ARC* newPtr;
VERTEX* vertFromPtr;
VERTEX* vertToPtr;
newPtr = new ARC();
if (!newPtr) { // failed to alloc
return -1;
}
// find fromKey
vertFromPtr = this->first;
while (vertFromPtr && (this->compare(fromKey, vertFromPtr->data) > 0)) {
vertFromPtr = vertFromPtr->pNextVertex;
}
if (!vertFromPtr || (this->compare(fromKey, vertFromPtr->data) != 0)) {
return -2; // failed to find fromKey
}
// find toKey
vertToPtr = this->first;
while (vertToPtr && (this->compare(toKey, vertToPtr->data) > 0)) {
vertToPtr = vertToPtr->pNextVertex;
}
if (!vertToPtr || (this->compare(toKey, vertToPtr->data) != 0)) {
return -3; // failed to find toKey
}
++(vertFromPtr->outDegree);
++(vertToPtr->inDegree);
newPtr->destination = vertToPtr;
if (!vertFromPtr->pArc) {
vertFromPtr->pArc = newPtr;
newPtr->pNextArc = nullptr;
return 1;
}
// find insert point in adjacency arc list
ARC* arcPredPtr = nullptr;
ARC* arcWalkPtr = vertFromPtr->pArc;
while (arcWalkPtr && (this->compare(toKey, arcWalkPtr->destination->data) >= 0)) {
arcPredPtr = arcWalkPtr;
arcWalkPtr = arcWalkPtr->pNextArc;
}
if (!arcPredPtr) {
vertFromPtr->pArc = newPtr;
}
else {
arcPredPtr->pNextArc = newPtr;
}
newPtr->pNextArc = arcWalkPtr;
return 1;
}연결하고자하는 정점들의 데이터들을 입력받아서 간선을 추가하는 메서드입니다.
먼저 새로 추가할 간선의 메모리를 할당한 후, insertVertex처럼 각 정점의 포인터를 찾아야합니다. 방법은 insertVertex때와 동일합니다. (line 4 ~ 29)
각 정점을 찾았다면, 간선의 출발지가 되는 정점의 outDegree의 값이 1 증가하고, 도착지가 되는 정점의 inDegree가 1 증가됩니다. (line 31 ~ 32)
그리고 해당 간선의 destination은 도착지의 정점이 됩니다. (line 33)
이제 해당 간선을 출발지 정점(vertFromPtr)에 추가해주어야 하는데, 만약 이전에 해당 정점에서 출발하는 간선이 하나도 없었다면, vertFromPtr->pArc에 추가될 간선의 주소를 대입해주고 메서드는 종료됩니다(line 34 ~ 38).
만약 이미 간선이 존재한다면, 새로 생성되는 간선이 추가될 위치를 탐색해야합니다(line 40 ~ ).
탐색하는 방법은 동일합니다. compare 함수를 통해서 살펴보는데, 추가될 간선의 도착지 정점의 데이터와 기존에 존재하는 간선의 도착지 정점 데이터 값을 비교해서 추가될 위치를 결정하게 됩니다.
deleteArc
template <typename T>
int DirectedGraph<T>::deleteArc(T fromKey, T toKey)
{
VERTEX* vertFromPtr;
VERTEX* vertToPtr;
// find fromKey
vertFromPtr = this->first;
while (vertFromPtr && (this->compare(fromKey, vertFromPtr->data) > 0)) {
vertFromPtr = vertFromPtr->pNextVertex;
}
if (!vertFromPtr || (this->compare(fromKey, vertFromPtr->data) != 0)) {
return -2; // failed to find fromKey
}
if (!vertFromPtr->pArc) {
return -3; // there is no adjacency edge
}
ARC* arcPredPtr = nullptr;
ARC* arcWalkPtr = vertFromPtr->pArc;
// find arc to tokey
while (arcWalkPtr && (this->compare(toKey, arcWalkPtr->destination->data) > 0)) {
arcPredPtr = arcWalkPtr;
arcWalkPtr = arcWalkPtr->pNextArc;
}
if (!arcWalkPtr || (this->compare(toKey, arcWalkPtr->destination->data) != 0)) {
return -3; // failed to find arc to tokey
}
vertToPtr = arcWalkPtr->destination;
// delete arc
--(vertFromPtr->outDegree);
--(vertToPtr->inDegree);
if (!arcPredPtr) {
vertFromPtr->pArc = arcWalkPtr->pNextArc;
}
else {
arcPredPtr->pNexetArc = arcWalkPtr->pNextArc;
}
delete arcWalkPtr;
return 1;
}간선을 이루는 두 정점의 값(fromKey, toKey)을 입력받아서, 그래프에 존재하는 간선을 삭제하는 메서드입니다.
간선은 출발지 정점의 연결리스트로 저장되어 있기 때문에 먼저 fromKey의 값을 갖는 정점만 찾으면 됩니다 (line 4 ~ 11).
만약 일치하는 데이터를 가진 정점이 없거나, 데이터는 일치하지만 해당 정점에서 나가는 간선이 없다면 삭제는 실패합니다 (line 13 ~ 19).
일치하는 정점(vertFromPtr)을 찾았다면, 이제 toKey의 데이터 값을 갖는 정점과 연결된 간선을 탐색합니다 (line 21 ~ 27). 마찬가지로 해당 간선이 존재하지 않는다면 삭제는 실패합니다 (line 29 ~ 31).
간선을 찾았다면, 해당 간선의 도착지 정점의 포인터 주소를 알 수 있고, 출발지 정점의 outDegree와 도착지 정점의 inDegree의 값이 1씩 감소됩니다 (line 32 ~ 36).
그리고 출발지 정점에서 찾은 간선 포인터 arcPredPtr->arcWalkPtr의 순서를 acrPredPtr->(arcWalkPtr->pNextArc)로 변경하고, arcWalkPtr을 메모리를 해제하면서 삭제를 완료하게 됩니다 (line 38 ~ ).

위와 같은 구조의 그래프를 어떻게 구성하는지 살펴보겠습니다.
먼저 사용될 데이터 형은 std::string 이므로, 이전에 설명드린 compare 함수를 사용하도록 하겠습니다.
#include <iostream>
#include <string>
#include "DirectedGraph.hpp"
int compare(const std::string& str1, const std::string& str2) {
if (str1 > str2)
return 1;
else if (str1 < str2)
return -1;
else
return 0;
}
int main(void) {
DirectedGraph<std::string> graph(compare);
graph.insertVertex("앨리스");
graph.insertVertex("아이린");
graph.insertVertex("밥");
graph.insertVertex("찰리");
graph.insertVertex("댄");
graph.insertVertex("에린");
graph.insertVertex("프랭크");
graph.insertVertex("조지");
graph.insertVertex("해리");
graph.insertVertex("재닛");
graph.insertVertex("케네스");
graph.insertArc("앨리스", "밥");
graph.insertArc("앨리스", "댄");
graph.insertArc("밥", "찰리");
graph.insertArc("댄", "에린");
graph.insertArc("에린", "찰리");
graph.insertArc("에린", "프랭크");
graph.insertArc("조지", "댄");
graph.insertArc("조지", "해리");
graph.insertArc("아이린", "조지");
graph.insertArc("아이린", "재닛");
graph.insertArc("재닛", "해리");
graph.printVertex();
return 0;
}DirectedGraph 클래스를 생성할 때, 사용될 compare 함수 객체에 std::string으로 구현한 compare 함수를 대입해주면 됩니다.
그리고 위 이미지의 그래프대로 각 정점을 삽입하고, 각 정점들을 연결하는 간선들을 추가해줍니다.

실행해보면, 모든 정점들과, 그 정점과 연결된 간선의 도착지가 '->' 다음에 나타나고 있습니다.
이렇게 방향이 있는 그래프를 구현을 완료했습니다.
전체 코드는 아래 깃헙에서 확인하실 수 있습니다 !
https://github.com/junstar92/DataStructure_Algorithm/tree/master/Data_Structure/Graph
GitHub - junstar92/DataStructure_Algorithm
Contribute to junstar92/DataStructure_Algorithm development by creating an account on GitHub.
github.com
'Data Structure & Algorithm > 자료구조' 카테고리의 다른 글
| [자료구조] Binary Search Tree(BST) (0) | 2020.09.09 |
|---|---|
| [자료구조] 우선순위큐(priority queue), 힙(heap) (0) | 2020.09.04 |
| [자료구조] 트리(Tree) (0) | 2020.09.03 |
| [자료구조] Queue(큐), Deque(덱) (0) | 2020.09.01 |
| [자료구조] Stack(스택) (0) | 2020.08.31 |




댓글