- 참조 문헌 및 사이트(Reference)
Data Structure : A Pseudocode Approach with C
Data Structure and Algorithm in C++
이번 글에서는 BST, 이진 탐색 트리에 대해서 알아보겠습니다.
이진 탐색 트리는 이진 트리이면서, 아래와 같은 성질을 갖고 있습니다.
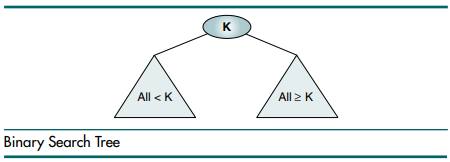
1. 루트 노드의 왼쪽 서브트리의 모든 Key는 루트 노드의 Key보다 작다. (All of left subtree < root)
2. 루트 노드의 오른쪽 서브트리의 모든 Key는 루트 노드의 Key보다 크거나 같다. (All of right subtree >= root)
3. 각 서브트리는 그 자체로 이진 탐색 트리이다.
여기서 Key는 노드의 데이터가 될 수도 있고, 다른 기준이 될 수도 있겠죠.
그림으로 나타내면 아래와 같이 나타낼 수 있습니다.
그리고 일반적으로 수를 데이터로 가지고 있는 경우에 아래와 같은 다양한 BST를 만들 수 있습니다.

위와 같은 모양의 BST를 만들 수 있는데, 여기서 (a)와 (b)는 완전 이진 트리로, 균형이 맞추어져 있습니다.
(d)의 경우에는 완전 이진 트리는 아니지만, 거의 완전 이진 트리이며 이것 또한 균형이 맞추어져 있다고 봅니다.
(c)와 (e)의 경우에는 완전 이진트리도 아니며, 편향된 BST 입니다.
다음으로는 BST의 연산에 대해서 알아봅시다.
기본적인 BST 연산에는 데이터의 삽입 및 삭제, 그리고 순회가 있습니다.
그리고 아래는 우리가 구현할 BST Class의 구성입니다. 여기서 BST 생성자에 compare 함수가 파라미터로 있는데, 이것의 사용방법은 마지막에 설명드리겠습니다.
template<typename T>
class NODE
{
public:
NODE(T data) : key(data), right(nullptr), left(nullptr) {}
T key;
NODE* right;
NODE* left;
};
template<typename T>
class BST
{
public:
BST(int(*compare)(T& arg1, T& arg2)) : size(0), root(nullptr), compare(compare) {}
~BST();
bool empty() const;
bool full() const;
bool insert(T data);
bool erase(T key);
void traversals() const;
private:
int size;
NODE<T>* root;
int(*compare)(T& arg1, T& arg2);
NODE<T>* _insert(NODE<T>* root, NODE<T>* newNode);
NODE<T>* _delete(NODE<T>* root, T key, bool* success);
void _destroy(NODE<T>* root);
void _preOrder(NODE<T>* root) const;
void _inOrder(NODE<T>* root) const;
void _postOrder(NODE<T>* root) const;
};두 개의 자식 노드와 키 데이터를 가진 노드 클래스와 root 노드를 가진 BST 클래스입니다. BST 클래스는 삽입과 삭제를 insert와 erase 함수로 수행할 수 있고, BST의 특성상 재귀로 구현이 가능해서, 내부 함수 _insert와 _delete를 통해서 삽입과 삭제를 수행하고 있습니다. traversals은 순회를 위한 함수로, 여기서는 전위, 중위, 후위 순회 모두 구현을 해보았습니다.
순회는 트리에서 이미 봤을테니, 순회를 먼저 살펴봅시다.

위와 같은 BST가 있을 때, 전위순회(preorder), 중위순회(inorder), 후위순회(postorder)의 결과는 다음과 같겠죠.
Preorder : 23 18 12 20 44 35 52
Inorder : 12 18 20 23 35 44 52
Postorder : 12 20 18 35 52 44 23
여기서 Inorder를 살펴봅시다. 중위순회한 결과, 크기 순서로 정렬된 시퀀스를 얻을 수 있습니다. 전위나 후위 순회는 순회는 맞지만 사실 그다지 쓸모가 있지는 않고, 중위순회의 경우에는 트리의 값들을 스퀀스하게 얻을 수 있어서 유용한 편입니다.
각 순회는 아래와 같이 구현할 수 있습니다.
template<typename T>
void BST<T>::traversals() const
{
std::cout << "Preorder : ";
_preOrder(root);
std::cout << "\nInorder : ";
_inOrder(root);
std::cout << "\nPostorder : ";
_postOrder(root);
}
template<typename T>
void BST<T>::_preOrder(NODE<T>* root) const
{
if (!root)
return;
std::cout << root->key << " ";
_preOrder(root->left);
_preOrder(root->right);
}
template<typename T>
void BST<T>::_inOrder(NODE<T>* root) const
{
if (!root)
return;
_preOrder(root->left);
std::cout << root->key << " ";
_preOrder(root->right);
}
template<typename T>
void BST<T>::_postOrder(NODE<T>* root) const
{
if (!root)
return;
_preOrder(root->left);
_preOrder(root->right);
std::cout << root->key << " ";
}
다음으로는 삽입(insert) 연산입니다.
노드를 삽입하면 되는데, 삽입은 좀 간단합니다. 루트의 값을 비교하면서 루트보다 작으면 왼쪽으로, 크면 오른쪽으로 타고 내려가면서 빈 leaf 노드를 만났을 때, 노드를 삽입하면 됩니다.

위 BST에서 19를 삽입할 때, 노드부터 출발해서 19가 들어갈만한 위치를 찾는 거죠. 23보다 작으니 왼쪽으로, 그리고 18보다 크니 오른쪽으로, 마지막으로 20보다 작으니 왼쪽 서브트리로 가는데, 비어있으므로 20의 왼쪽 노드에 위치시키면 되는 겁니다. 38도 마찬가지로 동일한 과정을 거쳐서 위치하게 됩니다.
알고리즘 순서는 다음과 같습니다.
1. 새로운 노드를 생성하고, 만약 BST가 비어있다면 root에 새로운 노드를 할당합니다.
2. 만약 BST가 비어있지 않다면 내부함수 _insert를 호출합니다.
3. _insert에서 root가 비어있다면 새로운 함수를 반환합니다.
4. 그리고 root가 비어있지 않다면 root와 새로운 노드의 값을 비교해서 _insert 함수를 재귀호출합니다.
재귀 호출 과정을 따라가다가 결국 빈 leaf node가 발견되면(여기서 3번에 해당), 새로운 노드를 return해서 이전 root의 left나 right에 할당하게 되는 겁니다. 아마 코드를 보면 더 이해가 빠를 것 같습니다.
위 내용은 다음과 같이 구현할 수 있습니다.
template<typename T>
bool BST<T>::insert(T data)
{
if (full())
{
std::cout << "BST is full\n";
return false;
}
NODE<T>* newNode = new NODE<T>(data);
if (size == 0)
root = newNode;
else
_insert(root, newNode);
size++;
return true;
}
template<typename T>
NODE<T>* BST<T>::_insert(NODE<T>* root, NODE<T>* newNode)
{
if (!root)
return newNode;
if (compare(root->key, newNode->key) > 0)
root->left = _insert(root->left, newNode);
else
root->right = _insert(root->right, newNode);
return root;
}
insert 함수에서 새로운 노드를 만들고 size를 확인하고, 비어있다면 root에 비어있지 않다면 _insert 함수를 호출합니다.
그리고 _insert 함수에서는 재귀적으로 호출되면서 새로운 노드의 위치를 찾습니다. 그리고 비어있는 위치를 만난다면 그곳에 새로운 노드를 위치하는 것이죠.
다음으로는 삭제 연산을 살펴보겠습니다. 삭제 연산은 삽입 연산보다 조금 까다로운데, 만약 중간에 위치한 노드가 삭제된다면 그 자리를 채워주는 로직이 필요하기 때문이죠. 그리고 만약 BST 내부에 중복되는 값이 있다면, 제일 먼저 발견된 값을 삭제합니다.
삭제에는 아래와 같이 4가지의 경우의 수가 존재합니다.
1. 삭제하는 노드에 자식 노드가 없는 경우
2. 삭제하는 노드에 오른쪽 자식 노드만 존재하는 경우
3. 삭제하는 노드에 왼쪽 자식 노드만 존재하는 경우
4. 삭제하는 노드에 왼쪽과 오른쪽 자식 노드가 모두 존재하는 경우
1번의 경우에는 삭제하는 노드가 leaf 노드이며, 단순히 삭제만 하면 됩니다.
2번과 3번의 경우에는 삭제할 노드 위치에 자식 노드를 연결해주고, 삭제하면 됩니다.
4번의 경우에는 두 가지의 방법이 존재하는데, 1)왼쪽 서브트리에서 가장 큰 노드를 삭제할 노드 위치로 옮기거나, 2)오른쪽 서브트리에서 가장 작은 노드를 삭제할 노드 위치로 옮기고, 삭제를 진행하면 됩니다다.
아래의 경우가 4번의 상황인데, 왼쪽 트리에서 가장 큰 노드를 옮겨서 삭제를 진행했군요.

다음으로 삭제 코드를 살펴봅시다. 역시나 재귀적 성질을 띄고 있기 때문에, erase 함수에서 _delete 함수를 재귀적으로 호출하면서 삭제할 노드를 찾아서 진행하게 됩니다.
template<typename T>
bool BST<T>::erase(T key)
{
if (empty())
return false;
bool success;
root = _delete(root, key, &success);
if (success)
--size;
return success;
}
template<typename T>
NODE<T>* BST<T>::_delete(NODE<T>* root, T key, bool* success)
{
if (!root)
{
*success = false;
return root;
}
if (compare(root->key, key) == 0)
{
NODE<T>* delNode = root;
if (root->left == nullptr)
{
root = root->right;
delete delNode;
}
else if (root->right == nullptr)
{
root = root->left;
delete delNode;
}
else
{
NODE<T>* exchNode = root->left;
while (exchNode->right)
exchNode = exchNode->right;
root = new NODE<T>(exchNode->key);
root->left = delNode->left;
root->right = delNode->right;
delete delNode;
root->left = _delete(root->left, exchNode->key, success);
}
*success = true;
}
else if (compare(root->key, key) > 0)
{
root->left = _delete(root->left, key, success);
}
else
{
root->right = _delete(root->right, key, success);
}
return root;
}그리고 삭제하려는 Key가 BST에 존재하지 않는 경우도 있기 때문에 삭제가 성공했는지 실패했는지 확인하는 용도로 success라는 변수를 두었습니다.
여기서 30 ~ 53 line을 보시면, 세 가지의 분기가 존재합니다. 오른쪽 자식노드만 존재할 때, 왼쪽 자식노드만 존재할 때, 양 쪽 자식노드가 모두 존재할 때 인데, 1번 경우인 leaf 노드인 경우에는 첫 번째 분기에 걸려서 코드가 수행됩니다. 왼쪽 자식노드를 새로운 root로 연결시켜주는데 어짜피 왼쪽 자식노드 또한 null 포인터이기 때문에 신경을 쓰지 않아도 되는 부분이며 정상적으로 동작합니다.
그리고 42 ~ 50 line은 양쪽 자식노드가 모두 존재하는 경우의 분기인데, 여기서는 왼쪽 서브트리의 가장 큰 노드를 찾아서, 삭제할 노드와 위치를 변경해주었습니다. 이렇게 변경을 해주어도 왼쪽 서브트리의 BST 성질은 유지됩니다.
그리고 왼쪽 서브트리에서 _delete 함수를 호출해서 삭제할 노드를 다시 찾아서 삭제를 하게 되는데, 삭제할 노드가 leaf 노드로 이동했기 때문에 큰 문제없이 1번 경우에 걸려서 삭제가 될 것입니다.
부가적으로 BST가 가득 찼는지, 비어있는지 확인하는 함수도 있지만, 설명은 생략하도록 하겠습니다.
BST의 시간복잡도를 한 번 살펴볼까요.

BST는 모든 leaf 노드의 레벨의 차이가 0 ~ 1인 균형을 유지하는 트리라면(balanced tree)인 경우에 N개의 노드가 존재할 때 BST의 탐색 시간은 평균 O(longN)이 걸리게 됩니다.

반면에 위와 같이 한 쪽으로 편향된 트리라면(not balanced tree)인 경우에는 최대 O(N)의 시간이 걸리게 됩니다.
이러한 문제 때문에 자동으로 밸런스를 맞추어주는 트리들이 존재하는데, AVL 트리, 레드-블랙 트리 등이 있습니다.
C++의 map 컨테이너 같은 경우가 레드-블래 트리로 구현되어 있죠.
자동으로 균형을 맞추어주는 트리에 대해서는 다음에 한 번 알아보도록 하겠습니다.
마지막으로 아까 언급했던 BST 생성자에 compare라는 함수 포인터가 있습니다. 현재 BST를 템플릿을 사용해서 어느 자료형에서나 적용이 가능하도록 만들었는데, 비교 함수는 따로 설정을 해주어야합니다.
여기서는 int 형에 대해서 설명을 드렸는데, 그렇다면 다음과 같이 compare 함수를 만들어줄 수 있겠죠.
int compare(int& arg1, int& arg2)
{
if (arg1 > arg2)
return 1;
else if (arg1 == arg2)
return 0;
else
return -1;
}따라서 만약 다른 사용자 타입의 자료형을 사용한다면, 이러한 함수를 직접 정의해서 BST를 생성할 때 적용을 해주면 됩니다.
사실 순회 함수내에서 직접 cout으로 출력하는 것이 아닌, 자료형에 맞게 출력할 수 있도록 다른 함수도 필요하지만, 따로 구현을 하지는 않았습니다.. 이 부분은 다음에 AVLTree나 다른 자료구조에 대해서 구현할 때 한 번 살펴보도록 해보겠습니다.
마지막으로 C++에서는 STL로 set이나 map을 제공하기 때문에, 그냥 사용하시면 되지만 이렇게 구현해보는 것도 이해하는데 엄청 도움이 되니 직접 구현을 해보는 것을 추천드립니다.
전체코드는 아래 경로에 있습니다.
github.com/junstar92/DataStructure_Algorithm/tree/master/Data_Structure/Tree
'Data Structure & Algorithm > 자료구조' 카테고리의 다른 글
| [자료구조] Directed Graph (0) | 2021.10.04 |
|---|---|
| [자료구조] 우선순위큐(priority queue), 힙(heap) (0) | 2020.09.04 |
| [자료구조] 트리(Tree) (0) | 2020.09.03 |
| [자료구조] Queue(큐), Deque(덱) (0) | 2020.09.01 |
| [자료구조] Stack(스택) (0) | 2020.08.31 |




댓글