References
- 리얼월드 알고리즘
KMP 알고리즘과 라빈-카프 알고리즘에 이어서 다른 문자열 알고리즘인 보이어-무어-호스풀(Boyer-Moore-Horspool) 알고리즘에 대해서 알아보겠습니다.
2020.11.25 - [Data Structure & Algorithm/알고리즘] - KMP 알고리즘
2020.12.17 - [Data Structure & Algorithm/알고리즘] - Rabin-karp(라빈 카프) 알고리즘
KMP 알고리즘이나 라빈-카프 알고리즘은 주어진 텍스트를 왼쪽에서 오른쪽으로 살펴봤습니다.
이와는 반대로 보이어-무어-호스풀 알고리즘은 오른쪽에서 왼쪽으로 텍스트를 스캔합니다.
아래는 'APESTLEINTHEKETTLE'이라는 텍스트에서 보이어-무어-호스풀 알고리즘을 사용하여 패턴 'KETTLE'을 어떻게 찾아가는지 보여줍니다. 그럼 하나하나씩 살펴보도록 하겠습니다.

먼저 패턴 'KETTLE'을 텍스트의 시작 부분에 놓고 패턴의 오른쪽부터 왼쪽으로 타켓 텍스트와 비교합니다.
그러면 패턴의 마지막 문자인 E와 텍스트의 접두사 'APESTL'의 마지막 문자 L이 서로 달라서 매칭이 실패했음을 바로 알 수 있습니다. 읽은 문자 중 가장 오른쪽 문자가 L이므로 다음 매칭 작업은 'APESTL'의 L 위치에 'KETTLE'의 L이 위치할 수 있게 KETTLE을 이동시킨 후에 다음 매칭을 진행합니다. 이동하면 아래와 같습니다.
위 이미지에서 i는 텍스트의 인덱스로, 왼쪽부터 오른쪽으로 0부터 인덱싱됩니다.
r은 패턴의 인덱스인데, i와 반대로 패턴의 오른쪽에서부터 0으로 시작됩니다. 또한, 텍스트의 인덱스 i가 다음 매칭을 위해 r만큼 이동해야한다는 것을 의미합니다.
'KETTLE'의 위치를 이동시킨 후에 다시 오른쪽에서 왼쪽으로 일치하는지 체크합니다.
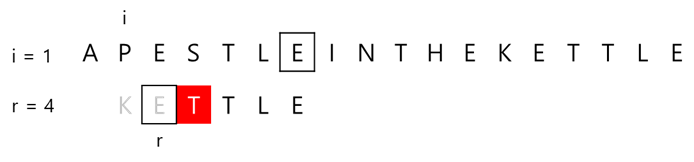
이번에는 패턴의 문자 T에서 매칭이 실패했습니다. 이때, 텍스트에서 마지막 문자는 'APESTLE'의 문자 E이므로 최선의 방법은 패턴의 다음 E가 텍스트의 접두사 'APESTLE'의 마지막 글자 E와 일치하게끔 패턴을 오른쪽으로 이동시키는 것입니다. 이때, r의 값은 4입니다.

이동을 시키면, 그 결과 첫 문자(패턴의 오른쪽 마지막 문자)에서 바로 불일치가 발생합니다. 게다가 읽은 텍스트의 문자는 H로 패턴에는 H가 존재하지 않습니다. 따라서 H의 오른쪽 다음 글자까지 패턴을 이동시키게 되며, 이때, r의 값은 6이 됩니다. 따라서, 패턴이 이동되면 i는 11이 됩니다.

이동 후에 다시 매칭을 시작해보면, L과 E로 불일치가 일어나 맨 처음의 상황과 같은 상황이 됩니다. 다시 오른쪽으로 한 칸 이동시키면 i = 12가 되고 텍스트에서 패턴을 찾을 수 있습니다.

위에서 살펴본 것과 같이 이 알고리즘은 텍스트에서 수많은 문자를 건너뛰면서도 제대로 작동합니다.
다만, 매번 패턴을 오른쪽으로 얼마나 많은 문자 수만큼 밀어야 하는지 알 수 있는 방법이 필요한데, 규칙은 간단합니다.
만약 텍스트에서 불일치가 발생했는데, 텍스트에서 불일치한 문자가 패턴에서 오른쪽부터 센 패턴의 위치 r에 있으면 패턴을 오른쪽으로 r만큼 이동시킵니다. 패턴에 같은 문자가 여러 번 나타날 수도 있는데, 이때 알고리즘이 동작하려면 r은 패턴에서 일치하지 않는 문자 중 가장 오른쪽에 있는 문자의 오른쪽부터 센 인덱스의 값입니다.
(이때, r의 값은 1 이상이며, 일치하는 문자의 위치 r이 0이라면 일치하는 문자가 없는 것처럼 이동합니다.)
아래 예시 참조바랍니다 !


따라서, 이 알고리즘을 제대로 동작시키려면 패턴에서 각 문자에 대해 가장 오른쪽에 있는 문자의 인덱스를 찾는 방법이 필요합니다. 그러기 위해서는 특별한 테이블을 만들어주어야 하는데, 이 테이블은 텍스트와 문자열의 알파벳(나올 수 있는 문자)만큼의 길이를 갖는 배열입니다. 보통 아스키 문자를 주로 사용하므로, 아스키 문자 기준으로 테이블을 생성한다면 테이블은 128개의 아이템을 갖습니다.
이 테이블을 rt라고 할 때 문자가 패턴에 있으면 패턴의 끝부터 세어서 rt[i]는 패턴에 있는 i번째 아스키 문자의 가장 오른쪽 인덱스(인덱스 \(r \req 0\))이며 만약 문자가 패턴에 없다면 rt[i]는 패턴의 길이 m으로 정의합니다.
첫 예시에서 패턴 'KETTLE'에서는 테이블 rt에서 69(E의 아스키코드 값), 75(K의 아스키코드 값), 76(L의 아스키코드 값), 84(T의 아스키코드 값)을 제외하고는 모든 엔트리의 값은 6입니다.

또 다른 예시로 패턴 'EMBER'을 살펴보면 다음과 같습니다.

여기서 R의 엔트리 값이 5(패턴의 길이)라는 것에 주목해보면, 이는 R에서 불일치가 일어나면 패턴을 패턴의 길이만큼 이동시킨 뒤에 다시 비교해야한다는 것을 의미합니다. 또한 \(r \req 1\) 조건인 불일치 문자 규칙의 정의와 일치합니다. 따라서 패턴에 나오지는 않는 다른 엔트리들과 같은 취급을 합니다. 이렇게 하면 이 위치에서 불일치가 발생할 때 패턴을 패턴의 길이만큼 이동시킬 수 있습니다.
나머지 아스키코드에 대한 엔트리값은 표시하지만 않았을 뿐, 위에 나타난 문자를 제외한 모든 아스키코드의 엔트리 값은 패턴의 길이 m으로 정의됩니다.
두 예시를 살펴보면, 두 예시 모두 테이블의 엔트리는 대부분 패턴의 길이와 같다는 것을 볼 수 있습니다. 이 때문에 이 알고리즘이 효율적인데, 이는 패턴에 포함되지 않는 대부분의 알파벳 문자가 나오면 패턴의 길이만큼 건너뛰게 된다는 것을 뜻합니다.
반대로 패턴에 문자가 많으면 이 알고리즘은 별로 효율적이지 않게 되지만, 실제로 그러한 경우는 드물기 때문에 크게 고려하지 않아도 좋습니다.
최우측 출현 테이블(rightmost occurrences table)
이렇듯 가장 오른쪽부터의 패턴 출현 순서 정보 테이블인 최우측 출현 테이블(rightmost occurrences table)을 만들어야하는데, 이 테이블을 생성하는 알고리즘은 다음과 같습니다. 예제에서는 아스키코드에 한정하여 이야기했지만, 알고리즘은 조금 더 일반적이라서 집합의 크기를 알 수 있는 어떤 종류의 문자 집합에도 적용할 수 있습니다.

(Ordinal(c)는 0부터 시작하여 알파벳 문자 c의 위치를 반환합니다.)
주의해야할 점은 패턴의 마지막 문자가 패턴의 다른 곳에 없으면 패턴의 길이만큼 이동시켜야 하기 때문에 두 번째 for문에서 마지막 문자는 체크하지 않는다는 것이고, 패턴에 동일한 문자가 여러 개 있다면 가장 오른쪽의 인덱스 값으로 설정되기 때문에 동일한 문자가 나타나면 테이블 엔트리 값이 갱신된다는 것입니다.
이를 코드로 구현하면 다음과 같습니다. 저의 경우 아스키코드로 한정을 시켰기 때문에 TABLE_SIZE가 128로 고정되어 있어서, 집합의 크기를 따로 파라미터로 전달받지 않습니다.
std::vector<int> createRtOccurrencesTable(std::string pattern)
{
std::vector<int> table(TABLE_SIZE);
const size_t m = pattern.length();
for (int i = 0; i < TABLE_SIZE; i++) {
table[i] = m;
}
for (int i = m - 2; i >= 0; i--) {
if (table[pattern[i]] == m) {
table[pattern[i]] = m - i - 1;
}
}
return table;
}7 ~ 9행에서 table의 모든 엔트리 값을 패턴의 길이 m으로 우선 초기화해주고, 11행부터 패턴의 오른쪽에서 왼쪽으로 진행하면서 table 엔트리 값을 설정해줍니다. 만약 table의 엔트리 값이 m이 아니라면, 가장 오른쪽에 있는 문자를 이미 발견했다는 의미이므로, 그냥 넘어가도록 했습니다.
이렇게 생성되는 테이블을 살펴보면, 패턴에 존재하는 문자가 아니라면 테이블의 엔트리 값은 패턴의 길이 m이 됩니다. 일반적으로 패턴의 길이가 그렇게 길지 않기 때문에 알파벳 집합의 크기로 배열의 생성하는 것은 공간을 낭비하는 경향이 있습니다. 아스키코드인 경우에는 128개만 존재하지 때문에 그리 크지 않지만, 빅데이터가 일반적인 요즘에는 공간을 너무 많이 낭비할 수 있습니다.
이 경우에는 해시테이블이나 집합과 같은 다른 자료 구조를 사용하여 테이블을 생성할 수 있는데, 해시테이블을 사용한다면 보이어-무어-호스풀 알고리즘을 수행할 때, 해시테이블에 존재하지 않는 문자면 패턴의 길이 m만큼 이동하고, 존재한다면 설정된 인덱스만큼 이동하도록 하면 됩니다.
저는 다음과 같이 구현하였습니다.
std::map<char, int> createRtOccurrencesTableUsingHash(std::string pattern)
{
std::map<char, int> table;
const size_t m = pattern.length();
for (int i = m - 2; i >= 0; i--) {
if (table.find(pattern[i]) == table.end()) {
table[pattern[i]] = m - i - 1;
}
}
return table;
}보이어-무어-호스풀 알고리즘
이 테이블을 가지고 수행되는 보이어-무어-호스풀 알고리즘은 다음과 같습니다.

꽤 간단합니다. 1~4행까지는 준비 단계로 반환할 큐를 생성하고, 패턴의 길이와 텍스트의 길이를 미리 구해놓고, 사용할 문자 테이블을 구합니다.
그리고 6행~13행의 루프에서 실제 알고리즘이 수행되는데, 위에서 살펴봤던대로 프로세스가 진행됩니다.
(6행 while문) i가 n-m을 넘어서면 패턴이 텍스트의 범위를 넘어서기 때문에 조건을 걸어두었습니다.
(7~9행) j를 m - 1로 설정하여 오른쪽부터 검사하도록 인덱스를 설정하고, 일치하는지 확인합니다.
만약 모든 문자가 일치하면 8행 while문을 빠져나온 j의 값이 -1이기 때문에 이를 확인하여 큐에 인덱스를 push하고, 그렇지 않다면 push없이 다음 위치로 이동합니다.
텍스트 마지막 위치의 문자를 가지고 i를 이동하는 것이 12~13행에서 이루어집니다.
시간 복잡도
보이어-무어-호스풀 알고리즘에서 최악의 경우를 살펴보면, 알고리즘의 외부 루프에서 \(n-m\)번 반복되고, 내부 루프에서는 \(m-1\)번 반복되는 경우입니다. 이 결과 실행 시간은 \(O(nm)\)이 되는데, 이는 무작위로 대입 매칭하는 것과 동일합니다.
최선의 시나리오는 마지막에 패턴과 일치되는 텍스트를 찾을 때까지 계속 m개의 문자 수만큼 반복적으로 건너뛰는 경우입니다. 이 경우에는 실행 시간이 \(O(n/m)\)인데, 실제라고 하기에는 너무 좋아보이는 실행시간이지만, 대부분의 실제 검색은 찾으려는 문자열이 작은 수의 알파벳으로 되어 있어 평균적으로 \(O(n/m)\)의 실행시간이 됩니다.
여기서 테이블을 생성하는데 \(O(m + s)\)만큼 시간이 걸리는데 일반적으로 n이 m + s보다 길어서 영향이 크기 않습니다.
전체 코드는 아래 깃헙에서 확인 가능합니다!
https://github.com/junstar92/DataStructure_Algorithm/tree/master/Algorithm/BoyerMooreHorspool
'Data Structure & Algorithm > 알고리즘' 카테고리의 다른 글
| 최소 신장 트리 (Minimum Spanning Tree) (0) | 2022.04.11 |
|---|---|
| 피보나치 수열 (0) | 2021.10.26 |
| [그래프] 플로이드-워셜 알고리즘(Floyd-Warshall Algorithm) (0) | 2021.10.11 |
| [그래프] 벨만-포드 알고리즘(Bellman-Ford Algorithm) (0) | 2021.10.10 |
| [그래프] 다익스트라 알고리즘(Dijkstra's algorithm) (0) | 2021.10.07 |




댓글