(Tensorflow v2.1.0)
이번 게시글에서는 머신러닝 입문에서 자주 사용되는 sklearn.dataset에 있는 iris dataset을 사용해서 붓꽃을 분류해보도록 하겠습니다.
먼저 필요한 package들을 import를 하고 시작해보도록 하겠습니다.
import sklearn.datasets
import tensorflow as tf
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
1. Dataset 준비
iris dataset은 sklearn에서 제공하는 데이터를 사용할 것입니다.
아래처럼 iris 데이터를 읽어오고, pandas DataFrame를 생성해서, 데이터가 어떻게 구성되어 있는지 살펴봅니다.
iris_data = sklearn.datasets.load_iris()
dataset = pd.DataFrame(data=np.c_[iris_data['data'], iris_data['target']], columns=iris_data['feature_names']+['target']).astype('float32')
dataset.head()
데이터를 살펴보면, sepal(꽃받침) 길이와 두께, petal(꽃잎) 길이와 두께가 있고, 해당 sample의 종류가 무엇인지 'target'을 통해서 나타내고 있습니다. iris_data의 'target_names'를 보면 어떤 target의 class의 종류를 알 수 있습니다.
iris_data['target_names']> array(['setosa', 'versicolor', 'virginica'], dtype='<U10')
0 : setosa / 1 : versicolor / 2 : virginica 라는 것을 알 수 있습니다.
그리고, dataset.describe()을 통해 dataset의 구성을 살펴보면,
dataset.describe()
총 150개의 example이 있다는 것을 알 수 있습니다.
저는 여기서 100개의 example만 training set으로 사용하고, 나머지 50개의 example은 test set으로 사용할 예정입니다. 그래서 데이터를 나누어주어야 하는데, 데이터를 가만히 보면 target이 class별로 뭉쳐있기 때문에 우선 셔플을 통해 무작위로 섞어주고, 100개와 50개로 나누었습니다.
dataset = dataset.sample(frac=1).reset_index(drop=True)
dataset.head()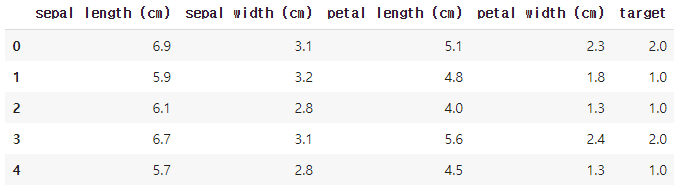
이렇게 나누어진 데이터를 가지고, training set과 test set을 만들어 주었습니다.
m_train = 100
m_test = 50
num_features = 4
num_classes = 3
x_train = dataset.iloc[:m_train, :num_features]
y_train = dataset.iloc[:m_train, num_features]
x_test = dataset.iloc[m_train:, :num_features]
y_test = dataset.iloc[m_train:, num_features]
print(f'x_train shape : {x_train.shape}') # (100, 4)
print(f'y_train shape : {y_train.shape}') # (100, )
print(f'x_test shape : {x_test.shape}') # (50, 4)
print(f'y_test shape : {y_test.shape}') # (50, )(*y_train과 y_test를 살펴보면 shape가 (n, ) 꼴로 나타나는데, 이는 1차원 벡터라는 것이고 여기서는 pandas의 series의 형태를 가지고 있습니다. tensorflow 행렬 연산의 결과가 1차원인 경우에는 (n, )꼴로 나오기 때문에 만약 비교하려는 y의 orig 데이터의 꼴이 (n, 1)이 된다면 계산이 정상적으로 되지 않는 경우가 발생합니다.)
normalization
그리고 아까 dataset를 보면, 각 feature들의 분포(최대, 최소값 등)이 전부 다르다는 것을 볼 수 있습니다. 학습을 제대로 시키기 위해서 각 feature의 평균과 표준편차를 구해서 \(x_{\text{norm}} = \frac{x - \mu}{\sigma}\)의 꼴로 normalization해줍니다. 주의할 것은 training set/test set 각각 따로 mean, std를 구하는 것이 아닌 전체 datatset에서 mean과 std를 구해서 training_set과 test_set에 모두 적용해줍니다.
# normalization
x_train = (x_train - mean) / std
x_test = (x_test - mean) / std
x_train.describe()
얼추 평균 0, 표준편차 1에 가까운 결과를 얻을 수 있습니다.
2. 학습
학습은 아주 기본적인 Logistic Regression으로 진행할 것입니다. 그리고 분류해야하는 class가 binary가 아니기 때문에 multi-class classification를 위한 one-vs-all 방법을 사용해서 분류할 것입니다.
Hypothesis Function으로는 sigmoid function을 사용할 것이고, cost function으로는 cross entropy를 사용해서 구할 것입니다.
수식으로 나타내면 다음과 같습니다.
\[h(W, b, X) = \frac{1}{1 + e^{-(X\cdot W + b)}}\]
\[\mathscr{L}(\hat{y}, y) = -\sum_{i = 1}^{m}(ylog(\hat{y}) + (1 - y)log(1-\hat{y}))\]
Logistic Regression과 one-vs-all에 대한 자세한 내용은
2020/08/07 - [Coursera 강의/Machine Learning] - [Machine Learning] Logistic Regression 1
를 참조하시길 바랍니다.
def logistic_regression(X, W, b):
return tf.math.sigmoid(tf.matmul(X, W) + b)
def compute_cost(y_hat, y):
y_orig = tf.one_hot(y, num_classes)
cost = -tf.reduce_mean(tf.reduce_sum(y_orig*tf.math.log(y_hat) + (1-y_orig)*tf.math.log(1-y_hat), 1))
return cost
def predict(y_hat):
return tf.argmax(y_hat, 1)
def accuracy(y_pred, y):
correct_pred = tf.equal(y_pred, tf.cast(y, tf.int64))
return tf.reduce_mean(tf.cast(correct_pred, tf.float32))logistic_regression은 hypothesis function을 계산하기 위한 함수이며, compute_cost로 loss를 계산합니다.
compute_cost에서 tf.one_hot 메소드가 사용됬는데, multi-class 분류문제이기 때문에, 결과값 y가 (m, 1)이 아닌 (m, num_classes)가 되도록 해줍니다.
그리고, 아래 predict함수는 hypothesis function으로 계산된 \(\hat{y}\)는 각 class에 속할 확률을 나타내므로, 가장 높은 확률을 가진 class로 분류해주는 역할을 합니다.
accuracy 함수는 실제 class와 비교해서 얼마나 정확하게 맞추었는지를 반환해주게 됩니다.
그리고, 학습을 위한 코드는 다음과 같습니다.
def model(X_train, Y_train, X_test, Y_test, num_iteration=2000, learning_rate=0.01, opt='SGD'):
# parameter initialization
W = tf.Variable(tf.zeros([num_features, num_classes]), name='weight')
b = tf.Variable(tf.zeros([num_classes]), name='bias')
# select optimization algorithm
if opt == 'SGD':
optimizer = tf.optimizers.SGD(learning_rate=learning_rate)
elif opt == 'Adam':
optimizer = tf.optimizers.Adam(learning_rate=learning_rate)
costs = []
accs = []
for iter in range(1, num_iteration + 1):
with tf.GradientTape() as tape:
y_hat = logistic_regression(X_train,W, b)
cost = compute_cost(y_hat, Y_train)
# compute gradient
grads = tape.gradient(cost, [W, b])
# update gradient
optimizer.apply_gradients(zip(grads, [W, b]))
# predict
pred = predict(y_hat)
# compute accuracy
acc = accuracy(pred, Y_train)
# save status
costs.append(cost)
accs.append(acc)
# print status
if iter % 100 == 0:
print(f'{iter} iterations : cost = {cost}, acc = {acc*100} %')
# predict on test data
y_pred = predict(logistic_regression(X_test, W, b))
test_acc = accuracy(y_pred, Y_test)
print(f'acc on test data : {test_acc*100} %')
ret = {
'weight':W,
'bias':b,
'costs':costs,
'accs':accs
}
return ret기본적으로 batch Gradient Descent를 사용하도록 했고, 다른 최적화 알고리즘과 비교하기 위해서 Adam 최적화 알고리즘을 선택할 수 있도록 했습니다. 학습이 완료되면, test set에 대한 정확도를 출력하고, 파라미터들과 매 iteration에서의 cost와 정확도를 반환하게 됩니다.
1) tf.optimizers.SGD
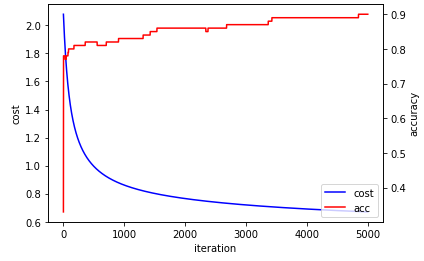
첫 번째로는 batch Gradient Descent(learning rate = 0.01, iteration = 5000)을 사용한 결과입니다. 매개변수의 값은 그냥 제 임의로 선택했습니다.
# SGD, iteration = 5000, learning_rate = 0.01
opt1 = model(x_train, y_train, x_test, y_test, num_iteration=5000, learning_rate=0.01, opt='SGD')
Training Accuracy가 90%, Test Accuracy가 92%가 나왔습니다. 100개의 example로 학습한 결과치고는 (매우) 잘 나온 것 같습니다.. !
2) tf.optimizers.Adam(learning rate = 0.01, iteration = 5000, 다른 파라미터는 기본값 사용)
다른 파라미터의 기본값은 beta_1=0.9, beta_2=0.999, epsilon=1e-07 입니다.
# Adam, iteration = 5000, learning_rate = 0.01
opt2 = model(x_train, y_train, x_test, y_test, num_iteration=5000, learning_rate=0.01, opt='Adam')
Adam 최적화 알고리즘을 사용한 결과, training set에서 96%의 정확도와 test set에서 98%의 정확도를 얻었습니다.. 이정도면 거의 완벽하게 맞췄다고 할 수 있네요.. ! 확실히 Adam 최적화 알고리즘이 더 훌륭하다라고 배운 것처럼 결과가 더 좋게 나오고 있습니다.
(Colab으로 진행했는데, 세션을 초기화하면 학습결과가 바뀌는 것을 발견했습니다.)
Adam 최적화 알고리즘에 대해서는 아래 게시글 참조바랍니다 !
2020/10/02 - [Coursera 강의/Deep Learning] - Optimization(최적화 알고리즘) : Mini-batch/Momentum/RMSprop/Adam
* Adam 최적화 알고리즘으로 시도해보다가 아래와 같은 경우가 발생한 경우가 있습니다.

검색을 통해서 알아본 결과, cost를 직접 수식으로 구할 때, log항에 0이 들어가서 무한대의 값이 나오기 때문일 수도 있고, 또는 learning rate가 너무 커서 overshooting이 일어났기 때문일 수도 있습니다.
1) log항의 값이 너무 작을 경우 1e-9로 고정시키는 방법
def compute_cost(y_hat, y):
y_orig = tf.one_hot(y, num_classes)
y_hat = tf.clip_by_value(y_hat, 1e-9, 1.)
cost = -tf.reduce_mean(tf.reduce_sum(y_orig*tf.math.log(y_hat) + (1-y_orig)*tf.math.log(1-y_hat), 1))cost를 구하는 함수에 tf.clip_by_value를 사용해서 y_hat의 최소값이 1e-9가 되도록 해주었습니다.
하지만.. !

결과는 달라지지 않았습니다.
그래서 직접 수식에 1e-9를 더해봤습니다.
def compute_cost(y_hat, y):
y_orig = tf.one_hot(y, num_classes)
cost = -tf.reduce_mean(tf.reduce_sum(y_orig*tf.math.log(y_hat+1e-9) + (1-y_orig)*tf.math.log(1-y_hat-1e-9), 1))
return cost
동일하게 cost에 nan가 나왔으나.. 이전과는 다르게 정확도가 유지되고 있습니다. 무슨 차이인지는 사실 잘 모르겠지만... 아마 파라미터가 유지되는 것으로 추측됩니다...
2) learning rate 조절
이번에는 compute_cost 함수는 그대로 두고, learning rate를 0.01에서 0.006으로 낮추어 봤습니다.
# Adam, iteration = 5000, learning_rate = 0.006
opt2 = model(x_train, y_train, x_test, y_test, num_iteration=5000, learning_rate=0.006, opt='Adam')
결과는 cost가 nan가 되지 않고, 정상적으로 학습이 되는 것으로 확인되었습니다.
아마 이 문제에서 cost가 nan가 된 것은 Gradient Descent에서 overshooting이 발생한 것으로 추측됩니다.
'ML & DL > tensorflow' 카테고리의 다른 글
| Cat Classification (1) : simple neural network (0) | 2020.11.15 |
|---|---|
| tensorflow에서 random seed 설정 (1) | 2020.11.14 |
| Logistic Regression with 1 hidden layer(planar data classification) (0) | 2020.11.13 |
| Linear Regression 간단한 예제 (4) | 2020.11.10 |
| TensorFlow 기본 동작 및 사용법 (0) | 2020.11.10 |



댓글