해당 내용은 Andrew Ng 교수님의 Machine Learning 강의(Coursera)를 정리한 내용입니다.
- Logistic Regression 로지스틱 회귀
이번 글과 다음 글은 classification(분류) 문제에서 주어진 data들을 discrete value(class)로 분류하기 위한 방법에 대해서 알아볼 것이다. 원하는 결과값 y는 분류된 class들 중에 하나에 속하게 된다.
분류(Classification)의 예시는 다음과 같다.
- Email : Spam or Not Spam ?
- Online Transactions : Fraudulent (Yes / No) ? - 온라인 거래 : 사기인지 아닌지
- Tumor : Malignant / Benign ? - 악성/양성 종양

위와 같이 2개의 class로 분류되는 문제를 binary classification이라고 하며, 편의상 class를 '0'과 '1'로 하자. 일반적으로 '0'은 negative class, '1'은 positive class'라고 한다. 나중에 두 개 이상의 class를 분류하는 multiclass classification에 대해서도 다루겠지만, 우선은 binary classfication 문제에 대해서 알아보자.
[Linear Regression for Classification]
어떻게 classification 문제를 추론할 수 있을까? 우선 우리는 기존에 배웠던 linear regression(선형회귀) 모델을 가져와서 classification 문제에 적용을 해볼 것이다. 종양 크기에 대한 악성/양성 구분 문제를 예시로 살펴보자.
기존에 배운 가설함수(hypothesis function)를 통하여 \(h_{\theta}(x) = \theta^{T}x\) 로 나타낼 수 있고, 아래와 같이 데이터가 표현된다.

이렇게 구한 가설함수의 값의 임계값(Threshold)을 '0.5'로 설정하여, 가설함수의 값이 0.5 이상이면 '악성', 그보다 작으면 '양성'이라고 판별했다.

꽤 적절하게 분류가 되는 것 같아 보이지만, 다른 데이터로 다시 시험해보자.

기존의 데이터에서 아주 큰 종양의 데이터가 추가되었다. 이때, linear regression 결과는 초록색 직선이 되지만, threshold를 0.5로 잡을 경우에 분류가 제대로 되지 않는다. 이처럼 분류 문제에 linear regression 알고리즘을 사용하게 되면 실패하는 경우가 많다.
또 다른 문제로는, 분류 문제는 '0'과 '1'로만 분류가 되어야 하지만, linear regression을 사용하게 되면 1보다 크거나 0보다 작은 값을 예측값 y로 추론할 수도 있다.

따라서 우리는 분류 문제를 해결하기 위해 linear regression이 아닌 Logistic Regression에 대해서 배울 것이고, 이는 가설함수가 0과 1사이의 값만 취할 수 있도록 한다.
[Hypothesis Representation]
우리는 Logistic Regression의 표현 모델에 대해서 알아볼 것이다. 앞서 말했듯이 Logistic Regression의 Hypothesis function은 0과 1 사이의 값만 내보내는 형태가 되어야 한다.
즉, \(0 \leq h_{\theta}(x) \leq 1\) 의 조건을 만족해야 한다.
위의 조건을 만족해야하는 상황에서 기존에 세운 가설함수 \(h_\theta(x) = \theta^{T}x\) 는 0과 1 사이의 범위를 만족하지 않고, 잘못된 예측을 할 수 있기 때문에 적합하지 않다. 따라서 Logistic Regression에서는 \(h_\theta(x) = g(\theta^{T}x)\) 로 가설함수를 표현한다. 여기서 g는 \(g(z) = \frac{1}{1 + e^{-z}}\) 이며, 정리하여 나타내면 아래와 같다.
$$h_\theta(x) = \frac{1}{1 + e^{-\theta^{T}x}}$$
이 그래프는 0과 1사이의 값만으로 표현되며, Sigmoid function 또는 Logistic function이라고 불린다.

이 가설함수의 출력값은 '주어진 input x에 대해서 y가 '1'일 확률을 의미한다.
만약, \(h_{\theta}(x) = 0.7\) 이라면, 이는 해당 input x가 악성 종양일 확률이 70%라는 의미이다.
일반적으로 다음과 같이 표현한다.
\(h_{\theta}(x) = P(y = 1 | x;\theta)\) - "probability that y = 1, given x, parameterized by \(\theta\)"
또한, \(h_{\theta}(x) = 0.7\) 를 거꾸로 말하면 양성 종양일 확률이 30%라는 의미이며, 일반적으로 \(h_{\theta}(x) = P(y = 0 | x;\theta)\) 으로 표현한다.
즉, 아래와 같은 위의 일반식은 다음과 같은 성질을 가지고 있다.

[Decision Boundary]
위의 가설함수 \(h_{\theta}(x) = g(\theta^{T}x)\), \(g(z) = \frac{1}{1 + e^{-z}}\) 에서 우리는 가설함수의 결과 값이 0.5이상이면 y는 '1', 0.5미만이면 y는 '0'이라고 추론할 수 있을 것이다.

즉, "y = 1" if \(h_{\theta}(x) \geq 0.5\)(\(\theta^{T}x \geq 0\))
"y = 0" if \(h_{\theta}(x) < 0.5\)(\(\theta^{T}x < 0\)) 이다.
다음으로 \(h_{\theta}(x) = g(\theta_0 + \theta_1x_1 + \theta_2x_2)\) 의 가설함수에 대해서 살펴보자.
만약 우리가 최적의 parameter \(\theta\)를 찾았고, 그 값이 \(\theta_0 = -3, \theta_1 = 1, \theta_2 = 1\) 이라면 다음과 같이 예측할 수 있다.
Predict y = 1 if
\(\underset{\theta^{T}x}{\underbrace{-3 + x_1 + x_2 \geq 0}}\)
따라서 \(x_1 + x_2 \geq 3\) 이면 '1'로 분류되고, 그렇지 않으면 '0'으로 분류된다. 이는 아래 분홍색 선으로 표현된다.
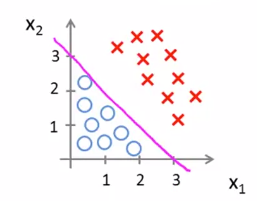
이때, Decision Boundary는 \(-3 + x_1 + x_2 = 0\) 이다. 이제 새로운 data가 추가되었을 때, \(x_1\) 과 \(x_2\) 값을 좌표로 찍어보고, decision boundary보다 위쪽에 찍히면 '1'로, 아래쪽에 찍히면 '0'으로 분류하면 되는 것이다.
Decision Boundary는 \(\theta\)에 의해서 결정되는 것이다. Training Data는 parameter \(\theta\)를 결정하는데 사용될 뿐, Decision Boundary에 직접적으로 영향을 끼치지는 않는다.
[Non-linear decision boundaries]
위의 예제는 classification이 선형적으로 분리되어 있는 데이터이다. 그러나 선형으로 class를 구분할 수 없는 경우도 있다. 예를 들어, 아래와 같이 원형으로 decision boundary를 설정해야 되는 경우도 있다.

이런 경우에 사용할 수 있는 한 가지 방법은 차수를 높혀서 다항식(polynomial)으로 표현하는 것이다. 이 방법을 사용하면 non-linear decision boundary도 표현할 수 있다. 만약 우리가 이미 적절한 pameter의 값을 구했고, 그 값이 \(\theta_0 = -1, \theta_1 = 0, \theta_2 = 0, \theta_3 = 1, \theta_4 = 1\) 이라면, 다음과 같이 예측할 수 있다.

- Predict "y = 1" if \(-1 + x_1^2 + x_2^2 \geq 0\)
- Predict "y = 0" if \(-1 + x_1^2 + x_2^2 < 0\)
즉, Decision Boundary는 \(x_1^2 + x_2^2 = 1\) 이다.
또한, 아래와 같이 더욱 복잡한 Decision Boundary를 갖는 경우도 있는데, 이러한 경우에도 차수(Dimension)을 높여서 표현할 수 있다.


'Coursera 강의 > Machine Learning' 카테고리의 다른 글
| [Machine Learning] Regularization 정규화 (0) | 2020.08.08 |
|---|---|
| [Machine Learning] Logistic Regression 2 (Cost Function, Gradient Descent, Multi-Class Classification) (5) | 2020.08.07 |
| [Machine Learning] Exam 1(Programming Assignment) (1) | 2020.08.07 |
| [Machine Learning] Octave 설치 / Vectorization(벡터화에대해서) (0) | 2020.08.07 |
| [Machine Learning] Computing Parameters Analytically (0) | 2020.08.04 |




댓글