해당 내용은 Andrew Ng 교수님의 Machine Learning 강의(Coursera)를 정리한 내용입니다.
Octave는 수치해석용 프로그램으로 Matlab의 대체재로 많이 쓰이며, Matlab과 호환성이 높다. 특히, 오픈소스로 무료로 사용이 가능하다.
[GNU Octave 설치]
다음 사이트에서 설치가 가능하다.
https://www.gnu.org/software/octave/download.html
Download
GNU Octave is a programming language for scientific computing.
www.gnu.org
설치 방법은 wiki를 참조하였다. (https://wiki.octave.org/Octave_for_Microsoft_Windows)
나는 Windows 를 사용중이므로, windows 용으로 진행하였다. .exe파일로도 받을 수 있고, 압축파일로도 받을 수 있는데, 따로 설치하기 싫어서 압축 파일을 다운받아서 단순히 압축만 풀고, 프로그램을 사용하였다. 압축을 풀게되면 아래와 같이 구성되어 있다. 압축을 풀때, 경로에 공백(space)과 아스키 문자가 아닌 경우에는 에러가 발생한다.
실행은 octave.vbs 파일을 실행하면 octave가 실행되지만, 실행하기 전에 post-install.bat 파일을 먼저 실행하자. 이것은 윈도우 폰트 캐시에 의한 plot delays를 줄여주고, 시스템이 미리 설치된 패키지들을 볼 수 있게 한다.

만약 명령프롬프트로 실행하고 싶으면, 바로가기를 만든 후에 속성 - 대상 끝에 --no-gui 라고 붙여주고 바로가기를 실행하면 된다.

명령프로프트는 위와 같이 실행이 된다.
기본적인 사용법은 다음에 정리를 해봐야겠다. 우선 여기서는 생략하도록 한다.
[Vectorization]
계산의 편의성을 위하여 일반적인 식들을 벡터화(Vectorization)을 하는 것이 중요하다. 이것은 계산 속도를 높혀줄 뿐만아니라 훨씬 더 적은 코드로 계산을 가능하게 한다.

예를 들어, 위와 같은 가설함수(hypothesis function)이 있고, j = 0에서부터 n까지의 합을 구한다고 하자. 우리는 이것을 조금 더 간단하게 계산하기 위해서 벡터로 만들어서 2번째 줄의 식처럼 두 벡터의 곱으로 나타낼 수 있다. 즉, Theta와 x를 n x 1 벡터로 만들어서 벡터 곱으로 나타내는 것이다.
벡터화를 하지 않았을 때의 코드와 벡터화를 하고 난 후의 코드는 아래와 같다.

벡터화를 하지 않았을 때, 4줄의 코드가 벡터화를 하고 나서는 단 한 줄로 표현될 수 있다.
C++ 코드를 예로 들어보자.
왼쪽은 벡터화를 하지 않고 for 문으로 함수의 합을 구한 것이고, 오른쪽은 선형대수학 라이브러리를 사용하여 벡터의 곱으로 구한 것이다.

마찬가지로 단 한 줄로 표현이 가능하다.
다음으로는 더 복잡한 Gradient descent(경사하강법)의 식을 살펴보자.

우리는 모든 j에 대해서 아래와 같이 theta()를 구하고 동시에 update해야한다.
간단하게 n = 2인 경우의 대해서 생각해보자. 우선 아래와 같이 모든 theta를 구해야 한다.
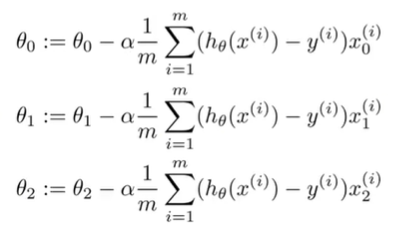
위 식을 벡터화하기 위해서 우선 복잡한 시그마 부분을 delta로 치환해서 표현한다.
여기서 theta는 0 ~ n까지의 n+1차원의 벡터고, alpha는 실수이다. 그리고, delta는 theta와 마찬가지로 n+1차원의 벡터이다. 각 항목들을 벡터로 표현하면, 아래와 같다.

그리고 delta의 합부분은 아래와 같다.

그리고 이전 강의에서 가설함수를 벡터로 표현하면 로 표현이 가능하며, X와 theta는 아래와 같다.

그리고, delta와 궁극적으로 구하려는 theta는 아래와 같이 표현이 가능하다. 이해가 잘 안된다면 아래 식을 벡터로 다 풀어서 직접 계산해보면 이해가 빠를 것이다. 여기서 y는 m x 1 벡터이다.

'Coursera 강의 > Machine Learning' 카테고리의 다른 글
| [Machine Learning] Logistic Regression 1 (1) | 2020.08.07 |
|---|---|
| [Machine Learning] Exam 1(Programming Assignment) (1) | 2020.08.07 |
| [Machine Learning] Computing Parameters Analytically (0) | 2020.08.04 |
| [Machine Learning] Multivariate Linear Regression (0) | 2020.08.04 |
| [Machine Learning] Gradient Descent (0) | 2020.08.04 |




댓글