해당 내용은 Andrew Ng 교수님의 Machine Learning 강의(Coursera)를 정리한 내용입니다.
이번 글에서는 이어서 Logistic Regression의 Cost Function, Gradient Descent, Multi-Class Classification에 대해서 알아볼 것이다.
[Cost Function]

이제 Logicstic Regression를 하기 위해서 필요한 \(theta\) 를 구하는 방법에 대해 알아보자.
앞에서 배웠던 Linear Regression을 위한 비용함수(Cost Function)은 \(J(\theta) = \frac{1}{2m}\sum_{i = 1}^{m}(h_\theta(x^{(i)}) - y^{(i)})\) 이며, 우리는 아래와 같이 표현할 수도 있다. 편의성을 위하여 위첨자 i는 생략하였다.
$$Cost(h_\theta(x), y) = \frac{1}{2}(h_\theta(x) - y)^2$$
Logistic Regression 문제를 위해 \(h_\theta(x) = \frac{1}{1 + e^{-\theta^Tx}}\) 를 대입하면 문제가 없을 것 같지만, 우리는 이 비용함수를 사용할 수 없다. 왜냐하면 위의 과정으로 대입한 비용함수 \(J(\theta)\) 는 Non-Convex 함수(볼록함수가 아님)이기 때문이다.

Linear Regression 에서의 비용함수는 Convex(Single bow-shaped) 구조로 Gradient Descent를 연산하면 수렴하면서 Global Minimum을 찾을 수 있었지만, Logistic Regression에서는 많은 Local Minimum(극소점)을 가지기 때문에 최소값을 보장할 수 없다.
따라서, 우리는 Logistic Regression을 위한 비용함수를 다음과 같이 정의한다.

이처럼 비용함수는 y = 1 일 때와, y = 0 일 때만 정의되어 있다.
(아래 두 그래프에서 cost 가 무한대인 경우에 \(h_\theta\) 와 cost 의 등호(=)가 잘못 표시되어 있습니다. '='가 아닌 '->'로 표시해야하며, 이는 0 or 1로 가까워 질수록 cost가 무한대에 가까워 진다는 것을 의미합니다.)
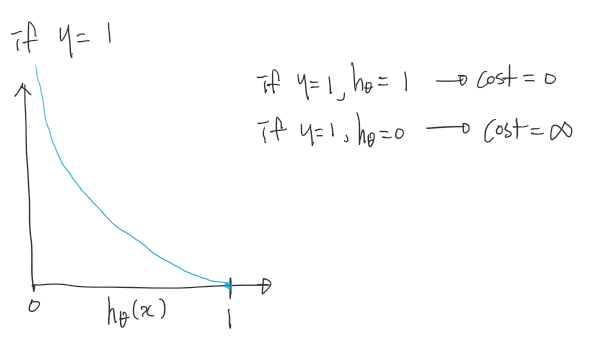
y = 1인 경우에, \(h_\theta(x) = 1\) 이면 Cost = 0 이지만, \(h_\theta(x) -> 0\) 이라면 Cost가 \(\infty\) 무한대라는 것을 알 수 있습니다. 이것이 의미하는 것을 이해하는 것은 중요하다. 잘못된 예측을 한 경우이므로, 매우 큰 Cost의 Penelty가 생기는 것을 의미한다(종양을 판단함에 있어서, 악성종양이지만 양성일 확률이 높다고 예측할 수 있다).

반대로 y = 0인 경우에는 그래프가 반대로 그려진다. \(h_\theta(x) -> 1\) 이면 \(Cost -> \infty\) 이고, \(h_\theta(x) = 0\) 이면 \(Cost = 0\) 이라는 것을 알 수 있다. 위와 마찬가지로 \(h_\theta(x) -> 1\) 이라고 판단하는 경우에는 위 그래프가 y = 0인 Class의 그래프이므로 예측이 완전히 잘못되었고, 그에 대한 penelty로 Cost가 무한대가 되는 것을 볼 수 있다. 반대로 \(h_\theta(x) = 0\) 인 경우에는 y = 0 이라고 올바른 예측을 하고 있고, Cost가 0이라는 것을 볼 수 있다.
y는 오직 '1' 또는 '0' 이라는 값만 가지므로, 나누어져 있는 비용함수를 간단히 다음과 같이 표현이 가능하다.
\(cost(h_\theta(x), y) = -ylog(h_\theta(x)) - (1-y)log(1 - h_\theta(x))\)
If \(y = 1, cost(h_\theta(x), y) = -log(h_\theta(x))\)
If \(y = 0, cost(h_\theta(x), y) = -log(1 - h_\theta(x))\)
즉, 하나의 식으로 표현해도, 우리는 y = 0 or y = 1 인 class에 대해서만 고려하기 때문에 결과적으로 동일하다. 또한, 다른 비용함수들도 많지만, 해당 모델이 Maximum likelihood estimation 원리로 유도되었고, Parameter \(\theta\) 를 구하는데 꽤 효율적이기 때문에 많이 사용된다.
정리하면, 아래와 같이 비용함수를 구할 수 있다.
우리는 \(J(\theta)\) 를 최소로 만드는 최적의 \(\theta\) 를 찾고, 이후에 새롭게 주어진 input x를 어떤 class로 분류할 지 판단하려면 \(h_\theta(x) = \frac{1}{1 + e^{-\theta^Tx}}\) 의 값이 0.5보다 큰지 작은지 확인하면 된다.
[Gradient Descent 경사하강법]
$$J(\theta) = -\frac{1}{m}\sum_{i = 1}^{m}\left [y^{(i)}logh_\theta(x) + (1 - y^{(i)})log(1 - h_\theta(x)) \right ]$$
이 Cost Function을 최소화하는 parameter \(\theta\) 를 찾는 것이 목적이다. \(J(\theta)\) 가 Convex 이므로, Gradient Descent를 통해 최적의 \(\theta\) 를 찾을 수 있다.
Reapeat {
\(\theta_j := \theta_j - \alpha\frac{\partial }{\partial \theta_j}J(\theta)\)
} simultaneously update all \(\theta_j\)
수식은 Linear Regression의 Gradient Descent와 동일하다. 다만 가설함수 hypothesis function이 \(h_\theta(x) = \frac{1}{1 + e^{-\theta^Tx}}\) 이다.
그리고, \(\frac{\partial }{\partial \theta_j}J(\theta)\) 을 계산하면 아래와 같다.
$$\frac{\partial }{\partial \theta_j}J(\theta) = \frac{1}{m}\sum_{i = 1}^{m}\left [h_\theta(x^{(i)}) - y^{(i)} \right ]x_j^{(i)}$$
[Advanced Optimization]
Gradient Descent 외에도 최적화된 Conjugate Gradient, BFGS, L-BFGS 알고리즘이 있다.

이 알고리즘의 장점은 Learning Rate 인 \(\alpha\) 를 자동으로 선택해주며, Gradient Descent 보다 종종 빠른 경우가 있다. 하지만 단점으로는 복잡하고 이해하기 어렵다. 간략히 소개만 하고 넘어가는데 여기서 따로 정리하지는 않겠다.
[Multi-Class Classification : One-vs-all]
MultiClass 분류 문제로 이메일을 자동으로 분류하는 예시를 살펴보자.
Works, Friends, Family, Hobby에 따라서 다른 폴더나 태그로 분류가 될 것이다. 이는 '0'과 '1'(binary classification)로만은 구분할 수 없다.
병 진단이나 날씨도 마찬가지로 binary classification으로는 충분하지 않다.

즉, binary classification 은 왼쪽 그래프와 같지만, Multi-Class classification은 오른쪽 그래프처럼 2개 이상의 class가 존재한다. 이처럼 class가 두 개 이상인 경우에는 어떻게 하면 될까 ?
이에 대한 방법으로 위 예시처럼 3개의 Class가 있는 Data Set이 주어졌을 때, 우리는 One-vs-all(one-vs-rest)이라는 알고리즘을 사용할 것이다.
이 알고리즘은 각 class 별로 (해당되는 class vs 나머지 class) 로 binary decision을 내리도록 만들어서 class 개수만큼의 binary classification 문제로 변환하여 해결하는 알고리즘이다.
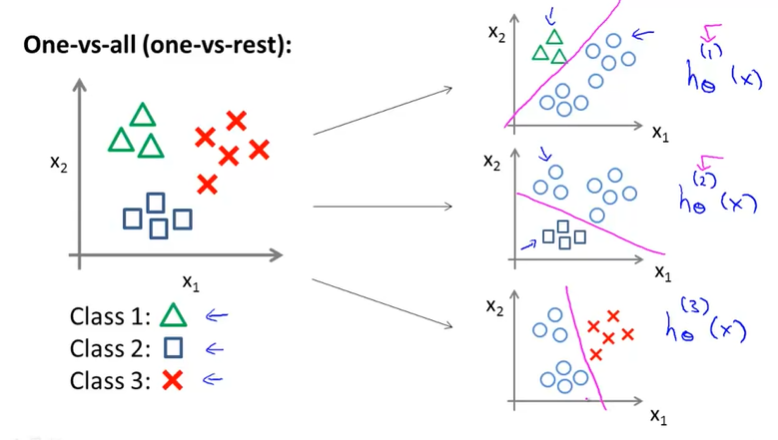
즉, Class 1, 2, 3에 대해서
- Class 1이 Positive Value 나머지 Class들은 Negative Value (\(h_\theta^{(1)}\) -> y가 Class 1에 속할 확률)
- Class 2이 Positive Value 나머지 Class들은 Negative Value (\(h_\theta^{(2)}\) -> y가 Class 2에 속할 확률)
- Class 3이 Positive Value 나머지 Class들은 Negative Value (\(h_\theta^{(3)}\) -> y가 Class 3에 속할 확률)
로 나타낼 수 있다.
Multi-Class classification 문제가 있으면, 각 class \(i\) 에 속할 확률 \(P(y = i)\) 를 구하기 위해 각 Class의 \(h_\theta^{(i)}(x)\) 를 구하고(train한다), 새로운 data x를 받으면 \(h_\theta^{(i)}(x)\) 가 최대인 i를 선택한다.
즉, \(h_\theta^{(i)}(x) = P(y = i | x;\theta), i \in \left \{ 1, 2, 3 \right \}\) 를 구해서, 'input x'에 대해서 가장 큰 확률(\(h_\theta^{(i)}(x)\)) 을 가지는 Class i를 선택(\(\underset{i}{max}h_\theta^{(i)}(x)\))한다.
'Coursera 강의 > Machine Learning' 카테고리의 다른 글
| [Machine Learning] Exam 2(Week 3) (3) | 2020.08.11 |
|---|---|
| [Machine Learning] Regularization 정규화 (0) | 2020.08.08 |
| [Machine Learning] Logistic Regression 1 (1) | 2020.08.07 |
| [Machine Learning] Exam 1(Programming Assignment) (1) | 2020.08.07 |
| [Machine Learning] Octave 설치 / Vectorization(벡터화에대해서) (0) | 2020.08.07 |




댓글