* Tensorflow 2 기준으로 작성됨
이번 글에서는 아주 간단한 선형회귀 문제를 tensorflow로 어떻게 구현할 수 있는지 알아보겠습니다.
필요한 package들을 import해주고, numpy를 사용해 X, Y data를 생성해줍니다.
import tensorflow as tf
import numpy as np
X = np.linspace(2, 10, num=50)
Y = np.random.rand(50)*10 + 2
Y.sort()
print('X = ', X)
print('Y = ', Y)
X, Y에 각각 50개의 값을 생성해주었으며, 아래와 같이 나타납니다.
import matplotlib.pyplot as plt
plt.plot(X, Y, 'ro')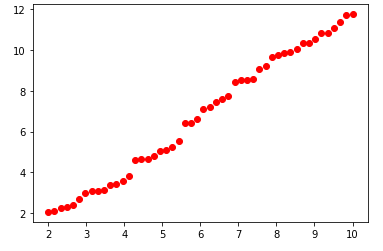
이제 선형회귀에 사용할 weight와 bias를 생성하고, 0 으로 초기화합니다. 각각 1차원 텐서가 됩니다.
W = tf.Variable(np.zeros(()), name='weight')
b = tf.Variable(np.zeros(()), name='bias')그리고, 선형회귀에 사용될 함수와 loss를 구하기 위한 함수를 구현해줍니다. tensorflow 1버전과 달라진 부분인데, session이 아닌 직접적인 함수로 수행하게 됩니다.
def linear_regression(x):
return W*x + b
def mean_square(y_pred, y):
return tf.reduce_mean(tf.square(y_pred - y))loss는 평균제곱오차(mean squar error:MSE)를 사용했으며, 아래와 같습니다.
\[\text{MSE} = \frac{1}{m}\sum_{i = 0}^{m}(\hat{y}^{(i)} - y^{(i)})\]
이제부터 머신러닝에 관련된 부분입니다.
최적화 알고리즘은 SGD로 지정하고, training step은 1000 epochs로 설정합니다.
(SGD는 Stochastic Gradient Descent를 의미하며, 이번 예제에서는 batch size를 설정하지 않기 때문에, 전체 dataset으로 Gradient Descent를 진행합니다. 따라서, Batch GD와 동일하게 동작합니다.)
epochs = 1000
optimizer = tf.optimizers.SGD()
for epoch in range(1, epochs + 1):
with tf.GradientTape() as t:
pred = linear_regression(X)
loss = mean_square(pred, Y)
# compute gradients
gradients = t.gradient(loss, [W, b])
# update W and b following gradients
optimizer.apply_gradients(zip(gradients, [W, b]))
if epoch % 50 == 0:
print(f'{epoch} epoch : loss = {loss}, W = {W.numpy()}, b = {b.numpy()}')그리고, 학습을 진행하는 코드를 작성합니다.
여기서 5 line에서 tf.GradientTape() API를 사용했는데, 이 API를 사용하면 context 안에서 실행된 모든 연산을 tape에 기록하며, 이후에 10 line처럼 t.gradient를 통해서 reverse mode differentiation을 사용해 기록된 연산의 Gradient를 계산하게 됩니다.
이렇게 구한 weight와 bias의 Gradient는 13 line의 코드에서 update됩니다. 마지막 if문은 진행사항을 살펴보기 위한 코드로 50 steps마다 진행과정을 출력합니다.

plt.plot(X, Y, 'ro', label='Origin data')
plt.plot(X, np.array(W*X + b), label='Fitted line')
plt.legend()
결과는 위 이미지의 파란색 라인처럼 됩니다.
'ML & DL > tensorflow' 카테고리의 다른 글
| Cat Classification (1) : simple neural network (0) | 2020.11.15 |
|---|---|
| tensorflow에서 random seed 설정 (1) | 2020.11.14 |
| Logistic Regression with 1 hidden layer(planar data classification) (0) | 2020.11.13 |
| Logistic Regression 예제(iris classification) (0) | 2020.11.13 |
| TensorFlow 기본 동작 및 사용법 (0) | 2020.11.10 |



댓글