해당 내용은 Coursera의 딥러닝 특화과정(Deep Learning Specialization)의 두 번째 강의 Improving Deep Neural Networks: Hyperparameter tuning, Regularization and Optimization를 듣고 정리한 내용입니다. (Week 1)
두 번째 강의에서는 어떻게 Neural Network(NN)이 잘 동작하게 할 수 있는 방법에 대해서 알아볼 것이다.
Hyper Parameter 튜닝과 Data 세팅까지 다루면서, 학습 알고리즘이 적절한 시간내에 학습이 될 수 있도록 해보자.
1주차에서는 NN을 만드는 것과 Regularization(정규화), 그리고 몇 가지 방법으로 NN이 제대로 구현되었는지 확인하는 방법에 대해서 알아볼 것이다.
- Setting up your Machine Learning Application
[Train/Dev/Test Sets]
Training Set, Dev Set, Test Set을 잘 설정하면 좋은 성능을 갖는 NN을 빨리 찾는데 도움이 될 수 있다.
NN에서는 다음과 같이 결정해야 할 것들이 있다.
- # of layer
- # of hidden unit
- Learning Rate
- Activation Function
처음 새롭게 NN을 구현할 때에는 적절한 하이퍼 파라미터 값들을 바로 선택하기는 거의 불가능하다. 그래서, 반복적인 과정을 통해 실험하면서 하이퍼 파라미터 값들을 바꿔가며 더 좋은 성능을 갖는 NN을 찾아야 한다.
경험이 많은 딥러닝 개발자들도 적절한 파라미터를 한 번에 선택하는 것은 거의 불가능하다. 그래서 오늘날 적용된 딥러닝은 반복적인 과정을 통해서 실험하면서 더 좋은 신경망을 찾아간다. 여기서 중요한 것은 우리가 이 반복적인 과정을 얼마나 효율적으로 하느냐이다.
여기서 우리는 데이터를 Train/Dev/Test Set를 적절하게 설정하면 훨씬 효율적으로 수행할 수 있다.

위와 같이 Data가 있을 때, 일부분을 Training/Dev/Test Set으로 분리할 수 있다.
Training Set에서 학습 알고리즘을 계속 수행하고, Dev Set을 통해서 다른 많은 모델 중에서 어떠한 모델이 가장 성능이 좋은지 평가한다. 그리고 가장 적합한 모델을 찾았으면, Test Set을 통해서 최종 모델을 평가하는 것이다.
일반적으로 Data Set을 70:30으로 Training Set과 Test Set으로 분리하거나, Dev Set, 즉, Cross Validation(CV) Set이 추가되면, 60:20:20으로 Training/Dev/Test Set으로 분리한다.
데이터가 100개, 1000개, 10000개의 경우에 이 비율로 나누는 것이 완벽하고 합리적이겠지만, 최근 빅데이터 세상에서는 데이터의 수가 수백만개가 넘어가기 때문에, 요즘은 Dev Set과 Test Set은 전체 Data에서 작은 비율을 차지한다. Dev Set이나 Test Set은 알고리즘을 평가하기에 충분하기만 하면 되기 때문에, 백만개의 Data가 있을 때, Dev Set과 Test Set은 10000개 정도면 충분하다. 물론, 데이터의 수가 작다면 60:20:20의 비율은 합리적일 수 있다.
자세한 가이드라인은 추후에 다시 언급하겠지만, 우리는 Dev Set을 통해서 다양한 모델들을 평가하고 개선하기 때문에 Dev Set은 Test Set와 같은 분포도를 가지는 것이 좋다.
또한, 결과적으로 bias가 없는 결과값이 목표이기 때문에 Test Set을 사용하는데, 만약 bias가 중요하지 않다면 Test Set은 없어도 괜찮을 것이다. 즉, Training Set으로 학습을 진행하고 다른 모델을 시도해보고, Dev Set에서 모델을 평가하고, 반복을 통해서 가장 좋은 모델을 찾는다. 이때, Dev Set을 Test Set으로 부르기도 한다.
이러한 방법은 알고리즘의 bias와 variance 문제를 더 효율적으로 계산하고, 개선할 수 있다.
[Bias / Variance]
Bias와 Variance 컨셉은 배우기는 쉽지만 마스터하기는 어려운 내용이고, 기본 컨셉을 배웠다고 하더라도 항상 예상하지 못하는 새로운 부분이 존재한다.
아래와 같은 Data 분포를 살펴보자.

첫 번째 high bias 그래프는 데이터가 잘 fitting 되지 않아서 underfitting의 문제를 가지고 있다. 반면에, 세 번째 high variance 그래프를 살펴보면 아주 복잡한 분류기(ex, DNN)에 fitting 시켰기 때문에, 데이터를 완벽히 fitting시켜서 overfitting 문제를 가지고 있다. 현재 이 그래프의 경우에는 \(x_1, x_2\) 두 개의 입력에 대해서 Decision Boundary를 그렸기 때문에 시각적으로 확인이 가능하지만, 고차원의 입력을 가지는 경우에는 시각적으로 확인이 어렵다. 그래서 다른 방법이 필요하다.
고양이 사진을 분류하는 예제를 가지고 살펴보자.

고양이 분류기가 있고, 입력 사진이 고양이라면 y = 1, 아니라면 y = 0으로 나타낸다. 여기서 우리가 살펴볼 핵심은 Train Set Error와 Dev Set Error이다. 일반적으로 사람은 완벽하게 고양이를 인식하기 때문에 Human Error는 0에 가깝게 된다.
그리고 Train Set Error와 Dev Set Error의 경우의 수를 살펴보자.

만약 Traini set error가 1%이고, Dev set error가 11%인 경우를 살펴보자. 이 경우에는 Training set에서는 아주 잘 동작하지만, Dev set에서는 잘 동작하지 못하는 것으로 볼 수 있다. 그렇다면 Training set에 overfitting했다고 할 수 있으며, 즉, 일반화하지 못했다고 볼 수 있고, High Variance문제를 갖고 있다고 할 수 있다.
두 번째로 Train set error가 15%, Dev set error가 16%라고 해보자. 이 경우에 Human error가 0%의 오류라고 한다면, 해당 알고리즘은 training set과 dev set 모두 잘 동작하지 못하고, 학습 알고리즘이 data에 잘 fitting 되지 않은 경우로 underfitting 문제라고 볼 수 있다. 그래서 이 알고리즘은 High Bias 문제를 갖고 있다고 할 수 있다.
세 번째로 Train set error가 15%고, Dev set error가 30%인 경우를 살펴보자. 두 번째와 마찬가지로 이 경우는 High bias 문제를 갖고 있다고 할 수 있다. 그리고, Dev set error과 train set error의 차이가 크기 때문에 trainig set에 overfitting해서 High variance 문제도 갖고 있는 최악의 경우라고 볼 수 있다.
마지막의 경우, train set error가 0.5%, dev set error가 1%인 경우가 있다. 이 경우에는 꽤 잘 동작한다고 볼 수 있다.
하지만, 이와 같은 분석은 Human error가 0%에 근접하거나 또는 Optimal Error(Bayes Error)가 거의 0%에 근접한다는 가정이 있어야지 올바르다.
만약 Optimal error or Bayes error가 15%라면, 두 번째 분류기의 경우는 사실 그리 나쁜 것은 아니고, High bias로 판단하지도 않을 것이다.
즉, 흐릿한 이미지가 있어서 사람도 잘 분류하지 못하고 시스템도 분류하지 못하는 사진이 있는 경우에는 조금 다를 수 있고, bias/variance 분석 방법이 다를 것이다.
자세한 내용은 나중에 다루겠지만, 여기서 중요한 것은 train set error를 살펴보면서 데이터가 얼마나 잘 fitting 하는지 확인하고, dev set에서 얼마나 variance problem이 존재하는지 확인한다.
(이러한 내용은 Bayes Error가 꽤 작고, train과 dev가 같은 분포라는 가정하에 성립하고, 이러한 가정이 부합하지 않는다면 다르게 접근해야한다.)
그렇다면 high bias와 high variance는 어떻게 발생한 것일까?

보라색 직선으로 분류되는 경우에는 데이터를 underfitting 하기 때문에 high bias를 가지고 있다. 이러한 분류기는 대부분 선형이며, 선형이기 때문에 underfitting 하게 된다.
만약 파란색 그래프처럼 데이터를 overfitting한다면, curve function이거나 2차함수이기 때문에 high variance 문제가 발생한다. 그리고 고차원의 입력을 갖는 경우에도 overfitting, 즉, high variance 문제를 가질 수 있다.
그리고 보라색 직선이지만 가운데 두 개의 샘플에 overffiting 하는 경우에는 high bias/high variance 두 가지 문제를 모두 가질 수도 있다.
[Basic recipe for machine learning]
위에 우리는 train set error와 dev set error를 통해서 bias나 variance 문제를 진단할 수 있다는 것을 배웠다. 이런 정보가 머신러닝의 시스템적인 부분을 알 수 있게 해주고, 이것을 머신러닝의 basic recipe라고 하며, 시스템적인 접근을 통해서 알고리즘의 성능에 기여할 수 있다.
basic recipe는 다음과 같다.
초기 모델을 학습한 이후에 해당 알고리즘이 high bias를 띄고 있는지 확인한다.
만약 high bias의 문제가 있다면 더 큰 network나 다른 구조의 NN을 선택하거나, 더 길게 학습을 진행하거나, 더 최적화된 알고리즘을 선택하는 방법도 있다.
high bias를 감소시켰다면, 다음으로 high variance 문제가 있는지 확인한다. 이때, dev set error를 통해서 살펴볼 수 있다.
만약 high variance 문제가 있다면, 더 많은 데이터를 수집하는 것이 문제를 해결하는데 가장 좋은 방법이다. 만약 데이터를 구할 수가 없는 상황이라면, regularization(정규화)를 시도할 수도 있다. 적합한 신경망 구조를 사용하는 것도 도움이 된며, 이 경우에는 high bias 문제도 해결할 수 있다.
보통 완벽한 방법을 찾는 것은 생각보다 어렵기 때문에, 보통 이러한 여러 가지 방법들을 시도해보고, 다시 체크를 하면 된다.
중요한 것은 high bias나 high variance에 따라서 시도할 수 있는 방법이 다르다는 점이다. 그래서 보통 train set error와 dev set error를 통해서 high bias/variance가 있는 경우에 해결방법을 찾아야하는데, 이처럼 우선 bias/variance 문제 여부를 확인하는 것이 적합한 방법을 찾는데 도움이 된다.
그리고 머신러닝 초기에는 bias-variance-tradeoff 에 대해서 많은 논의가 있었다. 왜냐하면, variance가 줄어들면 bias가 증가하고, bias를 즐이면 variance가 증가될 수 있었기 때문이다. 딥러닝 초창기에는 적용할 수 있는 방법이 많이 없어서, 한 가지 요소의 희생이 없이는 bais나 variance를 줄일 수 있는 방법이 딱히 없었다. 하지만 현재 빅데이터 시대에 맞게 더 큰 네트워크를 지속적으로 교육시킬 수 있어서, 왠만하면 더 큰 네트워크를 구성하면 bias는 variance에 영향을 미치지 않고 거의 항상 줄어든다고 볼 수 있다. 즉, 한 가지 요소를 해결하는데 다른 요소에 악영향을 미치지 않는다는 것이다. 이러한 이유때문에 딥러닝이 굉장이 유용하기도 하다.
- Regularizing your neural network
[Regularization]
만약 NN이 데이터에 overfitting 하다면, 그것은 high variance 문제가 있다는 것이고, 가장 먼저 시도해야될 방법 중에 하나는 Regularization(정규화)이다. 다른 방법으로는 더 많은 training data를 학습하는 것이다. 그러나 항상 데이터를 수집할 수는 없으며, 혹은 데이터를 수집하는데 비용이 너무 많이 들 수도 있다. 그래서 regularization항을 추가하는 것은 꽤 도움이 된다.
우선 Logistic Regression을 통해서 살펴보도록 하자.
Logistic Regression에서 우리는 비용함수 J를 최소화하는 파라미터 w, b를 구하는데 비용함수 J에 Regularization항을 추가하면 다음과 같다.
\[J(w, b) = \frac{1}{m}\sum_{i = 1}^{m}\mathscr{L}(\hat{y}^{(i)}, y^{(i)}) + {\color{blue}\frac{\lambda}{2m}\|w\|_2^2}\]
여기서 \(\|w\|_2^2 = \sum_{j = 1}^{n_x}w_j^2 = w^T \cdot w\) 이며, w의 norm에 아래첨자 2는 이 norm이 L2 regularization이라는 의미이다.
그리고 b에 대한 Regularization항 \(\frac{\lambda}{2m}b^2\)을 추가할 수도 있지만, 여기서는 생략하도록 하겠다. 왜냐하면 파라미터 b는 단순히 상수이며, 파라미터 w는 보통 높은 차수이기 때문에, b를 추가해도 큰 차이가 없다.
L2 regularization이 가장 일반적인 유형의 Regularization이다.
L1 regularization을 사용하면 다음과 같다. 아래첨자로 1이 붙은 것을 볼 수 있을 것이다.
\(\frac{\lambda}{2m}\sum_{j = 1}^{n_x}\|w_j\| = \frac{\lambda}{2m}\|w\|_1\)
만약 L1 regularization을 사용한다면, w 벡터 안에 0값이 많이 존재하게 되어서 sparse한 상태가 된다.
파라미터 set이 0이고, 모델을 저장하는데 더 적은 메모리를 사용해서, 모델을 압축하는데 유용하기도 하다. 하지만, 그렇게 많이 사용되지는 않고, 대체로 L2 regularization이 많이 사용된다.
(이 부분에 대해서 나중에 다시 알아봐야할 것 같음)
여기서 \(\lambda\)는 regularization parameter이다.
\(\lambda\)는 보통 dev set이나 cv set을 사용해서 적절한 \(\lambda\)값을 세팅하게 된다.
이것이 Logistic Regression에서의 regularization이고, NN에 대한 regularization을 살펴보자.
NN에서 Regularization항을 추가한 Cost Function J는 다음과 같이 정의된다.
\[J(W^{[1]}, b^{[1]}, \cdots, W^{[L]}, b^{[L]}) = \frac{1}{m}\sum_{i = 1}^{m}\mathscr{L}(\hat{y}^{(i)}, y^{(i)}) + {\color{blue}\frac{\lambda}{2m}\sum_{l = 1}^{L}\| W^{[l]} \|^2}\]
Regularization항에서 norm은 다음과 같다.
\[\|w^{[l]}\|^2 = \sum_{i = 1}^{n^{[l]}}\sum_{j = 1}^{n^{[l-1]}}(w_{i, j}^{[l]})^2\]
여기서 \(w^{[l]}\)는 \((n^{[l]}, n^{[l-1]})\) 차원이다.
이 \(w^{[l]}\)의 norm은 Frobenius라고 불리며, 아래첨자 F가 붙어서 \(\|w^{[l]}\|_{F}^2\)로 쓰이기도 한다.
다음으로는 어떻게 Regularization항을 Gradient에 추가하는지 살펴보자.
BP를 통해서 우리는 dW를 구했고, 이것은 \(\frac{\partial J}{\partial W^{[l]}}\) 이다.
그 후에 다음과 같은 식으로 파라미터 W를 업데이트 했다.
\[W^{[l]} := W^{[l]} - \alpha dW^{[l]}\]
Regularization항을 추가했기 때문에, dW는 다음과 같이 계산된다.
\[dW^{[l]} = \text{(from BP)} + {\color{blue}\frac{\lambda}{m}W^{[l]}}\]
그리고 파라미터는 다음과 같이 업데이트된다.
\[\begin{align*} W^{[l]} &:= W^{[l]} - \alpha \left [ \text{(from BP)} + \frac{\lambda}{m}W^{[l]} \right ] \\ &= W^{[l]} - \frac{\alpha \lambda}{m}W^{[l]} - \alpha\text{(from BP)} \\ &= (1 - \frac{\alpha \lambda}{m})W^{[l]} - \alpha\text{(from BP)} \end{align*}\]
\((1 - \frac{\alpha \lambda}{m})\)가 1보다 작은 값이기 때문에 L2 regularization은 'Weight Decay'(가중치 감쇠)라고 불리기도 한다.
[Why regularization reduces overfitting?]
Regularization은 high variance 문제, 즉, overffiting 문제를 해결하는데 도움이 되는데, 왜 도움이 될까?

위와 같은 신경망에 대해서 살펴보자.

이 신경망이 오른쪽 그래프처럼 overfitting한다고 가정한다.
그리고, Cost Function J는 다음과 같이 정의된다.
\[J(W^{[l]}, b^{[l]}) = \frac{1}{m}\sum_{i = 1}^{m}\mathscr{L}(\hat{y}^{(i)}, y^{(i)}) + {\color{blue}\frac{\lambda}{2m}\sum_{l = 1}^{L}\|W^{[l]}\|_F^2}\]
L2 Norm(or Frobenius Norm)은 weight 행렬이 너무 크면 줄여주는 역할을 한다. 왜 이러한 역할이 overffiting을 막아주는 것일까?
여기서 Lambda를 크게하면, W 값을 0에 가까운 값으로 만들 것이다. \(W^{[l]} \approx 0\)
이렇게 된다면, 아래 처럼 hidden unit의 영향을 거의 0으로 만들어 버릴 것이다.
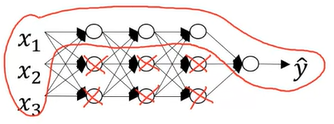
신경망을 더욱 심플하게 만들고, 단순히 여러 층으로 이루어진 Logistic Regression과 유사하다고 볼 수 있다.
이런 경우에 high bias 그래프 쪽으로 이동하게 되는데, 이상적으로 Lambda값을 적당한 값으로 설정해서 가운데 그래프와 같이 만들 수 있다.
실제로 hidden unit이 0이 되는 것은 아니고, 지속적으로 hidden unit은 사용되지만, hidden unit의 효과와 영향이 줄어든다는 것을 기억하자.
한 가지 예제를 더 살펴보자.

위와 같은 tanh 함수가 있을 때, z의 값이 작으면 우리는 빨간색으로 표시된 tanh의 선형 부분만 사용할 것이다.
Regularization에서 Lambda값이 크다면 \(W^{[l]}\)값이 작아지고, 결국에 \(Z^{[l]}\)의 값도 작아질 것이다.
\[\begin{matrix}\lambda \uparrow && \rightarrow W^{[l]} \downarrow && \rightarrow Z^{[l]} = W^{[l]}A^{[l-1]} + b^{[l]} \end{matrix}\]
이것은 Linear Regression처럼 모든 Layer가 선형적으로 동작할 것이고, 모든 층이 linear하다면 단순히 선형 네트워크가 될 것이다. Activation이 linear하기 때문에 비선형 decision이 불가능해서, overfitting할 수 없게 된다.
[Dropout Regularization]
L2 Regularization이외에 Dropout Regularization이라는 기법에 대해서 알아보자.

위와 같은 신경망이 존재하고 overfitting이 존재할 때, 우리는 각 layer에 노드를 제거하는 확률을 설정한다. 위에서는 0.5로 설정을 했는데, 절반의 노드가 제거되고, 이렇게 아래와 같이 감소된 네트워크로 우리는 FP와 BP를 진행할 것이다.

조금 이상한 테그닉으로 보일 수도 있고, 무작위로 노드를 삭제하지만 정상적으로 잘 동작한다.
Sample에 대해서 기존보다 더 작은 네트워크로 학습하기 때문에, regularization효과를 얻는다.
어떻게 구현하는지 알아보자.
Dropout을 구현하는 방법은 여러가지가 있는데, 'Inverted dropout'가 흔하게 사용되며, 이것을 알아보겠다.
예시로 신경망에서 3번째 layer에서 dropout의 적용을 살펴보자.
1. Dropout vector d를 생성한다.
d3 = np.random.rand(a3.shape[0], a3.shape[1])
2. 그리고 우리는 d3가 어떤 숫자(keep_prob)보다 작은지 확인한다. 여기서 keep_prob = 0.8이라고 하자. 그렇다면 노드가 제거될 확률이 0.2가 되는 것이다.
d3 = np.random.rand(a3.shape[0], a3.shape[1]) < keep_prob
이렇게 한다면, d3는 0.8의 확률로 1이 되고, 0.2의 확률로 0인 vector가 된다.
3. a3를 d3의 요소곱한다.
a3 = np.multiply(a3, d3)
4. 마지막으로 keep_prob로 나누어준다. 이것은 inverted dropout 테크닉이며 아래 예시를 통해서 왜 나누어주는지 알아보겟다.
a3 /= keep_prob
만약 50개의 units이 있는 layer라면, 10개의 units은 제거되어서 0이 될 것이다.
\(Z^{[4]} = W^{[4]}a^{[3]} + b^{[4]}\)이고, 우리는 \(a^{[3]}\)가 20퍼센트까지 감소한다는 것을 알 수 있다.
여기서 \(Z^{[4]}\)의 expected value값을 감소시키지 않기 위해서 a3에 0.8을 나누는 것이다. 그러면 a3의 expected value는 변하지 않고, z4의 expected value도 변하지 않을 것이다.
(keep_prob를 1로 설정하면 dropout을 적용하지 않는 것과 동일하다)
d3는 어떤 unit을 0으로 만들지 결정하는데 사용되며, FP와 BP에 모두 사용된다.
주의해야 할 점은 test set에서는 dropout을 사용하지 않는 것이다. 테스트에서 예측할 때 dropout을 사용하면, 예측값이 랜덤하게 되고, 결국에 예측값에 noise만 추가될 뿐이다. 그리고 keep_prob를 나누어주는 연산을 했기 때문에, 테스트에서 dropout을 사용하지 않더라도 테스트의 expected value는 변하지 않는다.
[Understanding Dropout]
Dropout은 무작위로 unit을 제거하는 역할을 하는데, Regularization이 어떻게 잘 동작할 수 있는 것일까?
이렇게 무작위로 unit을 제거하게 되면, 더 작은 NN으로 학습하는 것과 동일하기 때문에, 더 작은 NN을 사용하면 Regularization 효과를 가져야하는 것처럼 보인다.
단일 unit의 관점에서 살펴보자.

NN에서 dropout을 도입하게 되면, 위와 같이 unit이 제거될 수있고, 또는 다른 unit이 제거될 수도 있다.
이런 상황에서 의미있는 결과값이 되기 위해서는 보라색으로 표시된 unit이 어떤 한 가지 feature에 의존하면 안된다. 왜냐하면, dropout에서는 그 특성이 임의로 제거될 수도 있기 때문이다. 그래서 한 가지 입력에 큰 weight를 주는 것을 주저하게 된고, weight를 분산시키게 된다.
이렇게 weight를 분산시켜주면, weight의 norm을 축소시키는 효과가 있을 것이다. 따라서, L2 Regularization와 유사하게, weight를 줄이고 overfitting문제를 해결해준다.
아래와 같이 3개의 inpute feature가 있는 NN을 살펴보자.
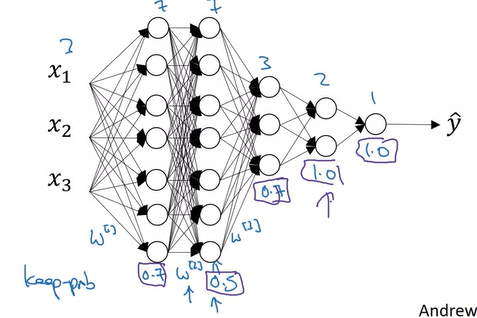
Dropout을 적용할 때, 우리가 선택해야 했던 매개변수 중에 하나는 바로 keep_prob인데, 이 값은 층별로 설정이 가능하다. 예를 들어, 첫번째 layer에는 0.7, 두번째는 0.5, 세번째는 0.7, 네번째, 다섯번째는 1로 설정할 수 있다. 1로 설정한 것은 dropout을 적용하지 않는다는 것이다.
W1은 7x3 matrix, W2는 7x7 matrix, W3는 3x7 matrix이고, W2가 가장 큰 matrix라고 볼 수 있다. 우리는 이 W2 matrix의 overfitting을 방지하기 위해서 두 번째 층의 keep_prob를 낮게 설정할 수 있을 것이다. 즉, overfitting이 우려되는 layer에는 keep_prob를 낮게 설정하고, 걱정되지 않는 layer에는 높게 설정하는 것이다.
keep_prob를 높게 설정하는 것은 L2 Regularization에서 Lambda값을 증가하는 것과 동일하다. (다른 layer보다 더 regularization하기 위해서)
엄밀히 말하자면, input layer에도 dropout을 적용할 수도 있지만, 잘 사용하지는 않는다.
Dropout의 단점
Dropout을 사용하게 되면 Cross-validation에서 설정해야할 하이퍼파라미터가 증가한다는 것이 단점이다.
또한, Cost Function J가 명확하게 정의되지 않는다. 매 반복마다 노드를 무작위로 제거하기 때문에, Gradient Descent 성능을 더블체크하기가 어렵다.
Dropout은 Computer Vision에서 도입되었다.
컴퓨터비전에서는 입력값의 크기가 너무 커서, 모든 픽셀들을 입력하는데 항상 데이터가 부족하다. 그렇기 때문에 컴퓨터 비전에서 자주 dropout이 활용된다. 컴퓨터 비전 리서치 연구원들은 dropout을 기본값으로 사용하는 사람도 있다.
기억해야할 것은 dropout은 regularization 기법이며, overfitting 방지에 도움이 주는 것이므로, overfitting이 아니면 사용하라고는 하지 않을 것이다.
컴퓨터 비전에서는 보통 데이터가 충분하지 않기 때문에 거의 항상 overfitting해서, 일부 컴퓨터 비전 연구원들은 dropout을 맹신하는 경우도 있다. 다른 분야에서는 그렇지 않은 경우가 많다.
[Other regularization methods]
L2 regularization과 dropout 외의 overfitting을 줄일 수 있는 다른 방법들을 살펴보자.

만약 데이터가 비싸고, 더이상 수집할 수 없는 경우에 Data augmentation 방법을 사용할 수 있다.
이미지를 가로로 뒤집거나, 회전하고 줌인하거나, 또는 찌그러뜨리거나 확대를 해서 Data set을 확장할 수 있다.
다만, 새로운 것 데이터를 추가하는 것보다는 좋지는 않지만 시간을 절약해주는 장점이 있다.
이 방법은 큰 비용없이 overfitting을 줄이는 방법이다.

Early Stopping은 Gradient Descent를 실행하면서 training set error나 J function과 dev set error 그래프를 그려서 W가 middle-size일 때, 중지시키는 방법이다. 학습 초기에 파라미터 W를 0에 가깝게 작은 값으로 초기화를 하고, 학습을 하면서 W는 증가하게 되는데, W의 비율이 중간정도되는 지점에서 중지하게 된다.
머신러닝의 단계는 아래와 같이 두 가지로 나누어진다.
1. Cost Function J를 최적화(Optimize cost function J) - Gradient Descent
2. Not Overfit - Regularization
이 두 단계가 서로 영향을 미치지 않도록 직교화(Orthogonalization)라는 용어가 있는데, 여기서는 설명없이 넘어가도록 한다.
Early Stopping을 사용하면, 위 두 단계가 함께 적용되고, 별개의 문제를 각각 따로 해결할 수가 없게 된다.
즉, overfitting을 해결하기 위해서 Gradient Descent를 중간에 멈추기 때문에, 최적화를 완벽하게 하지 못하고 J를 더이상 줄이지 못하게 된다. 이렇게 된다면 이후에 시도할 방법들을 더 복잡하게 만들게 된다.
그래서 Early Stopping 대신, L2 Regularization을 사용하는 경우에는 더 길게 학습하면되고, 여러 값의 Lambda를 테스트해야하지만 하이퍼파라미터를 분해하는데 도움이 된다.
다만, Early Stopping은 Gradient Descent 한번으로 W값을 설정할 수 있다.
그래서 단점이 있지만 종종 사용되는 방법이지만, 주로 L2 Regularization을 사용하는 것을 선호한다.(Computer 연산을 감안해야함)
'Coursera 강의 > Deep Learning' 카테고리의 다른 글
| [실습] Logistic Regression with a Neural Network(can / non-cat classifier) (0) | 2020.09.24 |
|---|---|
| Practical aspects of Deep Learning 2 (3) | 2020.09.23 |
| Deep Neural Network(DNN) (0) | 2020.09.20 |
| Shallow Neural Networks (8) | 2020.09.08 |
| Basics of Neural Network programming (Week 1, 2) (3) | 2020.08.30 |




댓글