해당 내용은 Coursera의 딥러닝 특화과정(Deep Learning Specialization)의 첫 번째 강의 Neural Networks and Deep Learning를 듣고 정리한 내용입니다. (Week 3)
이번 글에서는 Forward Propagation과 BackPropagation을 사용한 1개의 hidden layer를 가진 Neural Network를 알아보자.
[Key Concept]
- Understand hidden units and hidden layers
- Be able to apply a variety of activation functions in a neural network
- Build your first forward and backwarnd propagation with a hidden layer
- Apply random initialization to your neural network
- Become fluent with Deep Learning notations and Neural Network Representations
- Build and train a neural network with one hidden layer
[Overview]
우선 저번 시간에 보았던 Logistic Regression에 대해서 살펴보자.

우리는 위와 같은 Logistic Regression 모델에서 FP(Forward Propagation)을 통해서 아래와 같이 식들을 도출했다.

그 결과 Cost Function인 \(\mathscr{L}(a, y)\)를 구할 수 있었다. 그리고 BP(BackPropagation)을 통해서 미분항 da와 dz를 구했다.

여기서 da와 dz는 다음을 뜻한다.
\[\begin{matrix} da = \frac{\partial}{\partial a}\mathscr{L}(a, y), & dz = \frac{\partial}{\partial z}\mathscr{L}(a, y) \end{matrix}\]
다음으로 feature가 3개고 한 개의 hidden layer를 가진 NN(Neural Network)를 살펴보자.

이러한 NN을 2-layer NN이라고 하는데, input layer, hidden layer, output layer 3개의 층이 있지만 보편적으로 input layer은 고정된 값이므로 포함시키지 않아서 2-layer NN이라고 부른다.
그래서 첫 번째 layer는 hidden layer가 되고 두 번째 layer는 output layer가 된다.
위의 NN에서 FP와 BP를 진행하면 아래와 같이 진행된다.

input layer에서 hidden layer로 FP하는 과정을 살펴보면, Logistic Regression과 다른 점은 없다.
여기서 새로운 표기법이 나오는데, 위 첨자로 [1]이라고 붙었다. \(^{[1]}\)은 해당 값이 첫 번째 layer에 해당하는 값이라는 것을 의미한다.
따라서, 첫 번째 layer에서 FP를 진행하면서 \(z^{[1]} = W^{[1]}x + b^{[1]}\)와 \(a^{[1]} = \sigma(z^{[1]})\)를 구하고, 여기서 \(\sigma\)는 sigmoid function이다. 첫번째 layer, 즉, hidden layer에서 구한 \(a^{[1]}\)를 사용해서 output layer의 계산 값들, \(z^{[2]} = W^{[2]}a^{[1]} + b^{[2]}\)와 \(a^{[2]} = \sigma(z^{[2]})\)를 구할 수 있다. 마지막 layer이기 때문에 \(a^{[2]} = \hat{y}\) 이다.
이 결과값으로 Cost Function을 구하고, 다시 뒤로 돌아가면서 BP를 진행하면서 \(da^{[2]}, dz^{[2]}, dW^{[2]}, db^{[2]}\)를 구하고, 다시 \(da^{[1]}, dz^{[1]}, dw^{[1]}, db^{[1]}\)을 구하는 것이다.
위 과정이 NN에서 FP와 BP의 과정이다.
[Neural Network Representation]
NN에서 각 요소들을 어떻게 표현하는지 살펴보자.

위는 아까전에 살펴봤듯이, input layer/hidden layer/output layer, 3개의 층으로 이루어진 NN이다. 하지만 보편적으로 input layer는 포함시키지 않기 때문에 2-layer NN이라고 한다.(공식적인 표기, 논문에서 이렇게 쓰임)
Input layer에서 입력을 \(x\)라고 표현했는데, input feature값들은 \(a^{[0]}\)으로 표기할 수도 있다. 여기서 a는 activation을 뜻하고, 이 activation은 다음으로 이어지는 layer로 전달하는 값이다.
다음으로 Hidden layer에서도 activation을 계산하는데, 이것은 \(a^{[1]}\)으로 표현된다. 여기서 activation노드가 총 4개있는데, 위에서부터 \(a_1^{[1]}, a_2^{[1]}, a_3^{[1]}, a_4^{[1]}\)로 표현된다.
마지막으로 Ouput layer에서 \(a^{[2]}\) 값이 계산되며, 이 값은 실수이다.
지금 한 개의 training example에 대해 계산했기 때문에 \(\hat{y}\)에 위첨자가 없고, 여기서는 \(\hat{y} = a^{[2]}\)가 된다.
Hidden layer에는 관련된 매개변수 w와 b가 있을 것이고, 이것들은 \(w^{[1]}, b^{[1]}\)로 표현된다. 나중에 다시 보게되겠지만, 여기서 \(w^{[1]}\)는 4 x 3 Matrix이고, \(b^{[1]}\)는 4 x 1 Matrix이다.
비슷하게 Output layer에도 매개변수 \(w^{[2]}, b^{[2]}\)가 있는데, 각각의 Dimentation은 1 x 4, 1 x 1 Matrix이다.
이 Dimention에 관한 내용은 이어지는 내용에서 다시 다루겠다.
다음으로 NN에서 어떤 값들이 어떻게 계산되는지 살펴보자.
[Computing a Neural Network's Output]

Logistic Regression에서 한 개의 training example에 대해 위와 같이 계산되는 것을 볼 수 있다. z를 계산하고 sigmoid function을 적용해서 결과값이 나오게 된다.
NN에서는 한 개의 training example에 대해서 다음과 같이 계산된다. Hidden Layer의 첫번째와 두번째 activation노드의 계산을 살펴보자.
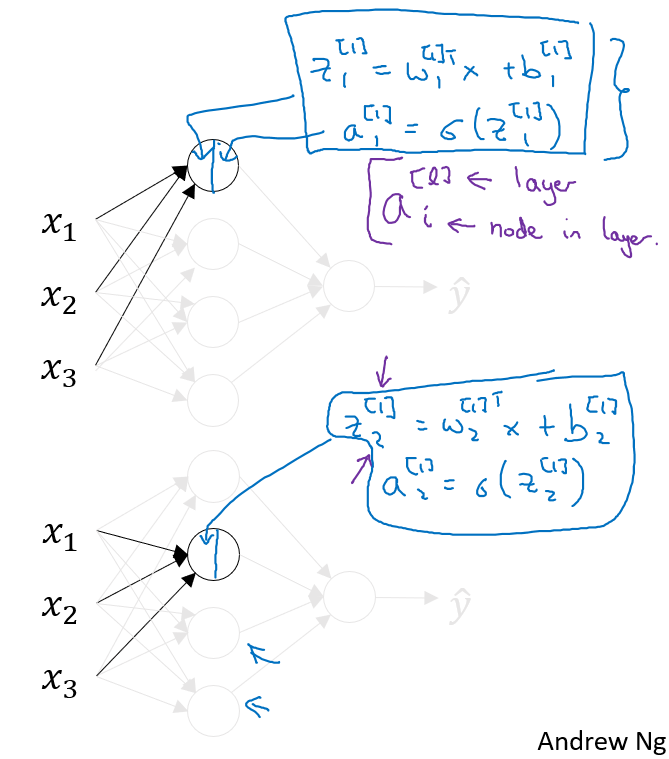
첫번째 activation노드에서 \(z_1^{[1]} = w_1^{[1]^T}x + b_1^{[1]}\)가 계산되고, 여기에 sigmoid function이 적용되어서 \(a_1^{[1]} = \sigma(z_1^{[1]})\)가 구하게 되며, 여기 \(a_i^{[l]}\)에서 \(l\)은 layer를 의미하고 i는 해당 layer에서의 i번째 노드를 의미한다.
마찬가지로 2,3,4번째 노드를 구하게 되면, 아래와 같이 구할 수 있다.

짐작했겠지만, 4개의 루프를 통해서 이 값들을 구하는 것은 비효율적이라고 생각할 수 있다. 그래서 이 식들을 가지고 우리는 벡터화를 시켜볼 것이다.
우선 \(z^{[1]}\)를 벡터로 계산하는 방법을 살펴보자.
먼저 W들을 가지고 행렬에 쌓아보면, 다음과 같이 나타낼 수 있다.
\[W^{[1]} = \begin{bmatrix} -- w_1^{[1]^T} -- \\ -- w_2^{[1]^T} -- \\ -- w_3^{[1]^T} -- \\ -- w_4^{[1]^T} -- \end{bmatrix}\]
이 W 행렬은 (4 x 3)의 차원이다.
그리고 x는 3개의 feature로 다음과 같이 나타낼 수 있다.
\[x = \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix}\]
나머지 \(b^{[1]}\)는 다음과 같이 (4 x 1) 벡터로 나타낼 수 있고, 이것들을 사용해서 \(z^{[1]}\)를 구하면 다음과 같다.
\[\begin{align*} z^{[1]} &= \begin{bmatrix} -- w_1^{[1]^T} -- \\ -- w_2^{[1]^T} -- \\ -- w_3^{[1]^T} -- \\ -- w_4^{[1]^T} -- \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} + \begin{bmatrix} b_1^{[1]} \\ b_2^{[2]} \\ b_3^{[3]} \\ b_4^{[4]} \end{bmatrix} \\ &= \begin{bmatrix} w_1^{[1]^T}x + b_1^{[1]} \\ w_2^{[1]^T}x + b_2^{[1]} \\ w_3^{[1]^T}x + b_3^{[1]} \\ w_4^{[1]^T}x + b_4^{[1]} \end{bmatrix} = \begin{bmatrix} z_1^{[1]} \\ z_2^{[1]} \\ z_3^{[1]} \\ z_4^{[1]} \end{bmatrix} \end{align*}\]
\(z^{[1]}\)는 이렇게 구할 수 있고, 이 값을 통해서 \(a^{[1]}\)을 구하면 다음과 같다.
\[a^{[1]} = \begin{bmatrix} a_1^{[1]} \\ a_2^{[1]} \\ a_3^{[1]} \\ a_4^{[1]} \end{bmatrix} = \sigma(z^{[1]})\]
그리고 Output layer에서 위와 같은 과정을 통해서 아래와 같이 \(z^{[2]}\)와 \(a^{[2]}\)를 구할 수 있다.
\[\begin{align*} z^{[2]} &= w^{[2]}a^{[1]} + b^{[2]} \\ a^{[2]} &= \sigma(z^{[2]}) = \hat{y} \end{align*}\]
여기서 \(w^{[2]}\)는 (1 x 4) Matrix, \(a^{[1]}\)는 (4 x 1) Matrix, \(b^{[2]}\)는 (1 x 1) Matrix 이다.
정리하면, 주어진 x에 대해서 다음과 같이 구할 수 있다. \(x\)는 \(a^{[0]}\)으로 표기할 수도 있다.

[Vectorizing across Multiple examples]
이제까지 한 개의 training example에 대해서 NN에서의 FP를 알아봤고, m개의 training examples에 대한 FP를 알아보도록 하자. 방금 우리는 한 개의 training example에 대해서

이제 m개의 training exmples에 대해서 모든 activation노드를 구해야하고, 우리는 한 개의 training exmple에 했던 방식으로 m개의 example에 적용해야한다.
여기서 \(a^{[2](i)}\)로 표현을 했는데, 여기서 위첨자 (i)는 i-th example을 의미한다.

m개의 example에 대해서 계산하려면 위처럼 for문을 통해서 계산을 해야하지만, Vectorization을 하면 반복문없이 계산할 수 있다.
우선 각 example x 벡터를 아래와 같이 쌓아보자.
\[X = \begin{bmatrix} | & | & & | \\ x^{(1)} & x^{(2)} & \cdots & x^{(m)} \\ | & | & & | \end{bmatrix}\]
여기서 모든 example에 대한 행렬이라는 뜻으로 대문자 X를 사용했고, X 행렬은 \((n_x, m)\) Matrix이다.
이제 for문에서 우리가 다음을 계산해야한다.
\[\begin{align*} Z^{[1]} &= W^{[1]}X + b^{[1]} \\ \rightarrow A^{[1]} &= \sigma(Z^{[1]}) \\ \rightarrow Z^{[2]} &= W^{[2]}A^{[1]} + b^{[2]} \\ \rightarrow A^{[2]} &= \sigma(Z^{[2]}) \end{align*}\]
각 example들을 열(column)로 쌓아서 X Matrix를 만든 것처럼, z와 a도 동일하게 진행하면 다음과 같이 적용할 수 있다.
\[Z^{[1]} = \begin{bmatrix} | & | & & | \\ z^{[1](1)} & z^{[1](2)} & \cdots & z^{[1](m)} \\ | & | & & | \end{bmatrix}\]
\[A^{[1]} = \begin{bmatrix} | & | & & | \\ a^{[1](1)} & a^{[1](2)} & \cdots & a^{[1](m)} \\ | & | & & | \end{bmatrix}\]
X, Z, A는 각 training example들을 가로로 indexing한 것이라고 볼 수 있다.
X에서 차원에서 행(row)는 feature의 개수 n이고, 열(column)은 Trainig Example의 개수 m이다.
그리고 Z, A에서 행(row)은 현재 layer의 activation node의 개수가 된다. 즉, (Hidden layer units x Training Example)의 차원을 가진다.
[Explanation for Vectorized Implementation]

방금 내용을 다시 정리하면 다음과 같다.
X와 A를 다음과 같이 training example이 행렬의 열에 오도록 아래와 같이 만들어준다.

그리고 for문으로 작성되었던 부분을 벡터화하여서 한 번에 계산해주면 된다.

[Activation Function]
이번에는 Hidden layer에서 어떤 Activation Function을 사용할 것인가에 대해서 알아보자.
지금까지 우리는 Sigmoid함수를 Activation Function으로 사용했는데, 때때로 다른 함수를 사용하는게 훨씬 나을 때도 있다.
이때까지 본 내용 중에서 우리는 Activation Unit을 구하는 두 단계가 있었고, Sigmoid 함수를 사용했었다.

이 Sigmoid 함수 대신 다른 함수를 사용할 수도 있으니, 조금 더 일반화시켜서 \(\sigma\)가 아닌 \(g(z)\)를 사용해서 식을 다시 표현해보겠다.
\[\begin{align*} \text{Given x}&: \\ &z^{[1]} = W^{[1]}x + b^{[1]} \\ &a^{[1]} = {\color{red}g^{[1]}(z^{[1]})} \\ &z^{[2]} = W^{[2]}a^{[1]} + b^{[2]} \\ &a^{[2]} = {\color{red}g^{[2]}(z^{[2]})} \end{align*}\]
여기서 \(g(z)\)는 비선형 함수이고, Sigmoid가 아닐 수도 있다. Activation function 중에 Sigmoid 함수보다 항상 더 좋은 성능을 발휘하는 함수가 있는데, 바로 tanh 함수이다. Hyperbolic tangent function 이라고 한다.

위와 같은 그래프를 가지며, -1에서 1 사이의 값을 가진다. tanh함수에서 \(a = \frac{e^z - e^{-z}}{e^z + e^{-z}}\) 이다. tanh 함수는 데이터를 중심에 위치시키려고 할 때, 평균이 0인 데이터를 갖게된다. 데이터를 중심에 위치시키는 효과 덕분에 다음 layer에서 학습이 더욱 쉽게 이루어지게 된다. Hidden Layer에서는 Simoid는 거의 사용하지 않을 것이고, tanh 함수는 거의 항상 Sigmoid보다 우수하다.
한 가지 예외가 있는데, Output layer에서는 Sigmoid를 사용한다. 왜냐하면 결과값 y는 0이거나 1인데, 예측값인 \(\hat{y}\)는 0과 1 사이의 값이며, -1과 1사이의 값이 아니기 때문이다. 그래서 이진분류 문제일 때, Output layer에서 Sigmoid 함수를 사용할 수 있다. (Output layer가 아니라면 sigmoid는 사용하지 않기를 권장)
따라서 여기서 \(g^{[2]}(z^{[2]})\)는 \(\sigma(z^{[2]})\) 이다.
이 예제에서는 tanh를 hidden layer의 activation 함수로 사용하고, output layer에서는 sigmoid를 activation 함수로 사용한다. 이미 표기를 했지만, layer마다 다른 activation 함수를 사용할 수 있기 때문에 위 첨자 [1], [2]를 사용해서 activation 함수가 다르다는 것을 표시한다.
Sigmoid와 tanh 함수는 한 가지 단점이 존재하는데, z가 매우 크거나 매우 작을 때, Gradient, 즉, 함수의 미분값(기울기)이 매우 작은 값이 된다. 따라서 z가 매우 크거나 작게 되면, 함수의 기울기는 거의 0이되고, Gradient Descent 알고리즘을 느리게 만드는 원인이 된다.
이러한 문제 때문에 머신러닝에서 자주 사용되는 activation 함수 중에 다른 하나는 Rectified Linear Unit, ReLU 함수이다. ReLU 함수는 아래처럼 생겼고, 공식은 다음과 같다.

\[a = max(0, z)\]
따라서, z가 양수일 경우에는 미분값은 1이고, z가 음수이면 미분값은 0이다. 수학적으로 z가 0인 지점, 즉 0에 매우 가까워지는 지점의 기울기는 구할 수가 없지만, 실제로는 걱정할 필요는 없다. 그래서 z가 0일 때, 우리는 미분값이 0이나 1인 것처럼 취급할 수 있고, 실제로 잘 동작한다. 수학적으로는 사실 미분이 가능하지 않다.
그래서 우리는 출력값이 0 또는 1인 경우에, output layer에는 sigmoid 함수를 activation 함수로 선택할 수 있고, 나머지 다른 layer에서는 ReLU 함수를 선택할 수 있다(기본적이다). 만약 hidden layer에서 어떤 activation 함수를 사용해야될 지 모르겠다면 그냥 ReLU 함수를 사용하면 된다. 가끔 tanh 함수도 사용하지만 방식이 대부분의 사람들이 사용하는 방식이다.
ReLU의 한 가지 단점은, z가 음수일 때 미분값이 0이라는 것이다.
여기에 약간 다른 버전의 ReLU가 있는데, 바로 Leaky ReLU라 부르는 함수이다. 이 함수는 z가 양수일 때는 ReLU와 동일하고, z가 음수일 때는 약간의 기울기를 갖게 된다. 다음과 같이 생긴 함수이다.

\[a = max(0.01z, z)\]
Leaky ReLU는 대게 ReLU보다 더 잘 동작하지만, 실제로 잘 사용하지는 않는다. (한 가지 선택하라고 한다면, ReLU를 선택)
ReLU와 Leaky ReLU의 장점은 이 함수에서 미분값, 즉, 기울기가 0과는 다른 값이라는 점이다. 실제로 ReLU 함수를 사용하면 NN이 종종 tanh나 sigmoid보다 훨씬 빠르게 동작하게 된다. 이러한 이유는 기울기에 의한 영향이 적다는 것인데, tanh나 sigmoid에서는 기울기가 0에 가까워져서 학습을 느리게 하는 경우가 있기 때문이다. z가 음수일 때, ReLU함수의 기울기는 0인데, 실제로 hidden layer에서 z의 값은 0보다 충분히 클 것이다. 그래서 학습이 빠르게 이루어질 수 있다.
Leaky ReLU에서 0.01이라는 파라미터를 곱해서 사용했는데, 다른 값을 사용할 수도 있다. 물론 더 잘 동작하는 경우도 있겠지만, 다른 값을 쓰는 경우는 잘 없다고 한다. 만약 다른 값을 사용하고 싶다면, 시도해보고 얼마나 잘 동작하는지 살펴보고 좋은 결과를 갖게 된다면, 사용하기를 권장한다.
NN을 동작시킬 때, 딥러닝의 주제 중의 하나는 다양한 선택지들이 존재한다는 것이다. hidden layer의 unit 수, activation 함수 선택, 파라미터 초기화 방법 등등이 있다. 어떤 것들이 최상으로 동작하는지 적절한 가이드라인을 제시하기는 어렵지만, 현장에서 어떤 방법들이 대중적으로 사용되는지 알려주도록 하겠다.
[Why do you need non-linear activation functions ?]
그렇다면 NN에서 왜 이런 activation 함수가 필요할까?
앞서 배운 FP 공식에서 \(g\) 함수를 \(g(z) = z\)로 linear activation 함수(identity function)를 적용해서 어떻게 되는지 살펴보자.

\(a^{[1]}, a^{[2]}\)는 그대로 \(z^{[1]}, z^{[2]}\)가 된다. 위 식에서 공식들을 다 대입해서 \(a^{[2]}\)를 구하면 다음과 같다.
\[a^{[1]} = z^{[1]} = w^{[1]}x + b^{[1]}\]
\[\begin{align*} a^{[2]} = z^{[2]} &= w^{[2]}a^{[1]} + b^{[2]} \\ &= w^{[2]}(w^{[1]}x + b^{[1]}) + b^{[2]} \\ &= W^{[2]}W^{[1]}x + W^{[2]}b^{[1]} + b^{[2]} \\ &= W'x + b' \end{align*}\]
이렇게 되면, 이 모델은 \(y\)와 \(\hat{y}\)를 선형함수로 계산하게 된다. 즉, NN은 선형함수에서 입력값에 대한 결과값을 주게 되는 것이고, 심층신경망으로 넘어갔을 때를 가정해본다면 NN이 몇 개의 layer로 이루어져있더라고 이것은 단순히 선형 activation 함수를 계산하는 것이다. 이런 경우에는 차라리 hidden layer가 없는 것이 좋다.
hidden layer가 일반 Logistic Regression과 비교했을 때, NN이 전혀 메리트가 있지 않게 된다.
중요한 것은 선형에서의 hidden layer는 거의 쓸모가 없다. 2개의 선형함수의 구성요소는 그 자체가 이미 선형함수이다. 그러므로 non-linear한 특성을 사용하지 않는 이상 더 흥미로운 결과를 낼 수 없을 것이다.
선형함수를 사용하는 한 가지 경우가 있는데, 그것은 \(g(z) = z\)인 경우이다. 만약 Y가 실수인 경우, 즉, 집값 예측 문제나 결과값이 이러한 실수로 나온다면 사용해도 괜찮을 것이다. 이 경우에도 hidden layer에서는 선형함수를 사용해서는 안된다. Sigmoid와 마찬가지로 output layer에서만 거의 사용된다.
물론 집값 예측에서 결과값은 모든 양수이기 때문에 ReLU 함수를 사용할 수도 있을 것이다.
[Derivatives of activation functions]
NN에서 FP를 진행한 후에, BP를 진행할 때 우리는 activation 함수의 미분, 기울기를 구해야 한다. 어떤 activation 함수인지 살펴보고, 어떻게 기울기를 구하는지 알아보자.(유도는 따로 하지 않음)
아래 sigmoid 함수가 있다.

sigmoid 함수의 미분을 구하면 다음과 같다.
\[\begin{align*} g'(z) = \frac{d}{dz}g(z) &= \frac{1}{1 + e^{-z}}(1 - \frac{1}{1 + e^{-z}}) \\ &= g(z)(1 - g(z)) \\ &= a(1 - a) \end{align*}\]
다음으로 tanh 함수의 미분을 살펴보자.

tanh 함수의 미분은 다음과 같다.
\[\begin{align*} g'(z) = \frac{d}{dz}g(z) &= 1 - (tanh(z))^2 \\ &= 1 - a^2 \end{align*}\]
ReLU 함수의 미분은 다음과 같다.

\[g(z) = max(0, z)\]
\[g'(z) = \left\{\begin{matrix} 0 & \text{if } z < 0 \\ 1 & \text{if } z \geq 0 \end{matrix}\right.\]
여기서 실제 수학적으로는 z가 0일 때는 미분값을 정의할 수 없지만, SW에 도입시키는 경우 0 또는 1로 지정한다. z가 정확히 0이 될 확률은 너무나도 작은 확률이라서 별로 상관이 없다고 생각하면 된다. 즉, z가 정확히 0일 때, 어떤 미분값을 설정하는지는 별로 상관이 없다는 것이다.
Leaky ReLU는 다음과 같다.

\[g(z) = max(0.01z, z)\]
\[g'(z) = \left\{\begin{matrix} -.-1 & \text{if } z < 0 \\ 1 & \text{if } z \geq 0 \end{matrix}\right.\]
[Gradient Descent for neural networks]
이번에는 1-hidden layer NN에 대해서 Gradient Descent를 진행해보자.
우리에게 필요한 파라미터와 Cost Function은 다음과 같다.
- Parameter : \(W^{[1]}, b^{[1]}, W^{[2]}, b^{[2]}\)
- Cost Function : \(J(W^{[1]}, b^{[1]}, W^{[2]}, b^{[2]}) = \frac{1}{m}\sum_{i = 1}^{m}\mathscr{L}(\hat{y}, y)\)
여기서 \(hat{y} = a^{[2]}\) 이고, 각 layer의 차원을 계산하기 위해 각 layer의 노드 개수를 \(n_x = n^{[0]}, n^{[1]}, n^{[2]} = 1\)로 정의한다.
그러면 파라미터들이 다음과 같은 차원을 가지는 것을 볼 수 있다.
\[\begin{matrix} W^{[1]} = (n^{[1]}, n^{[0]}) & b^{[1]} = (n^{[1]}, 1) \\ W^{[2]} = (n^{[2]}, x^{[1]}) & b^{[2]} = (n^{[2]}, 1) \end{matrix}\]
그리고 Gradient Descent는 다음과 같이 방식으로 진행한다.
\[\begin{align*} \text{Repeat } &\{ \\ &\text{Compute predicts }(\hat{y^{(1)}}, \cdots, \hat{y^{(m)}}) \\ &dw^{[1]} = \frac{\partial J}{\partial W^{[1]}}, db^{[1]} = \frac{\partial J}{\partial b^{[1]}}, \cdots \\ &W^{[1]} := W^{[1]} - \alpha dW^{[1]} \\ &b^{[1]} := b^{[1]} - \alpha db^{[1]} \\ &W^{[2]} := W^{[2]} - \alpha dW^{[2]} \\ &b^{[2]} := b^{[2]} - \alpha db^{[2]} \\ &\} \end{align*}\]
어떤 방법으로 위 식이 나오는 지는 조금 뒤에 설명하도록 하겠다.
위 식을 공식화해서 표현해보자.
Forward Propagation
\[\begin{align*} Z^{[1]} &= W^{[1]}X + b^{[1]} \\ A^{[1]} &= g^{[1]}(Z^{[1]}) \\ Z^{[2]} &= W^{[2]}A^{[1]} + b^{[2]} \\ A^{[2]} &= g^{[2]}(Z^{[2]}) = \sigma(Z^{[2]}) \end{align*}\]
BackPropagation
\[\begin{align*} dZ^{[2]} &= A^{[2]} - Y \\ dW^{[2]} &= \frac{1}{m}dZ^{[2]}A^{[1]^T} \\ db^{[2]} &= \frac{1}{m}np.sum(dZ^{[2]}, axis = 1, keepdim = True) \\ dZ^{[1]} &= W^{[2]}dZ^{[2]} * {g^{[1]}}'(Z^{[1]}) \\ dW^{[1]} &= \frac{1}{m}dZ^{[1]}X^T \\ db^{[1]} &= \frac{1}{m}np.sum(dZ^{[1]}, axis = 1, keepdim = True) \end{align*}\]
여기서 \(Y = \begin{bmatrix} y^{(1)} & y^{(2)} & \cdots & y^{(m)} \end{bmatrix}\) 이다.
그리고 \(dZ^{[1]}\)을 구하는 식에서 \(W^{[2]^T}dZ^{[2]}\)와 \({g^{[1]}}'(Z^{[2]})\)의 차원은 둘다 \((n^{[1]} , m)\)이고, 곱(*)은 행렬곱이 아닌 요소곱이다. 파이썬에서 계산하면 broadcasting 으로 자동으로 요소로 곱해진다.
그리고 np.sum으로 각 행을 다 더하는데, 파라미터로 axis = 1은 행은 유지하면서 각 행의 열을 모두 더하라는 의미이며, keepdims = True 파라미터를 통해서 계산된 결과가 rank 1 Matrix가 되지 않도록 차원을 유지시켜주는 역할을 한다. (이는 numpy를 익히면서 더 알아봐야겠다.)
[Backpropagation intuition]
(게시글이 너무 길어질 것 같아서, 따로 유도 부분을 정리하도록 하겠습니다.)
[Random Initialization]
NN에서 Weight(파라미터 W)를 랜덤으로 초기화하는 것은 중요하다. 이전 Logistic Regression에서는 weight를 0으로 초기화하는 것이 괜찮았지만, NN에서 모든 weight를 0으로 초기화하고 Gradient Descent를 적용하면 제대로 동작하지 않는다. 이유를 살펴보도록 하자.
만약 아래와 같은 NN이 있고, 모든 weight를 0으로 초기화하면 어떻게 될까?
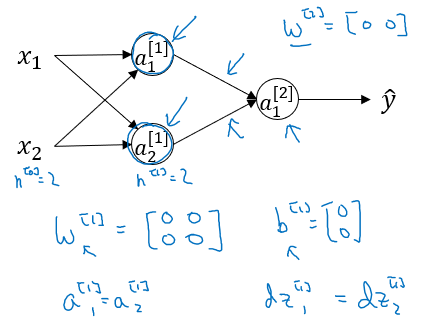
위 NN에서 \(W^{[1]}, b^{[1]}, W^{[2]}, b^{[2]}\)를 모두 0으로 초기화 했다고 하자. 여기서 bias term은 실제로 0으로 초기화해도 무방하다. w를 0으로 초기화하는 것이 문제가 된다.
이렇게 0으로 초기화하고, hidden unit을 구해보면, hidden unit이 똑같은 함수로 계산되기 때문에 결과는 \(a_1^{[1]} = a_2^{[2]}\)가 된다. FP로 결과값까지 도달한 후에, BP를 진행하면 대칭에 의해서 \(dz_1^{[1]} = dz_2^{[1]}\)이 된다.
즉 \(dW = \begin{bmatrix} u & v \\ u & v \end{bmatrix}\) 꼴이 되며, 이것들을 Symmetry(대칭)을 이룬다고 한다.
이렇게 되면, 매 iteration마다 이 hidden unit은 계속 똑같은 함수를 계산하게 된다.
그래서 w를 0으로 초기화하면 \(W^{[1]}\) hidden unit 모두 똑같은 함수로 계산되고, 2개의 hidden unit이 결과값에 동일한 영향을 주기 때문에, iteration 후에도 동일한 상황이 된다. 두 개의 hidden unit이 계속해서 대칭(Symmetric)이 된다.
위와 같은 문제의 해결책은 파라미터를 임의의 값으로 초기화하는 것이다.
즉, 아래와 같이 초기화를 할 수 있다.

\(W^{[1]}\)은 np.random.randn((2, 2)) 로 설정하는데, 이렇게 하면 가우시안 랜덤 변수로 생성되며, 이 숫자를 0.01과 같은 작은 값으로 곱해준다. 0.01은 예시이며, 다른값으로 초기화할 수도 있다. 다만, 보통 weight를 초기화하는데 우리는 임의의 작은 값을 선호하는데, tanh나 sigmoid 함수에서 weight가 만약에 너무 크면 activation 값을 계산할 때, z또한 매우 크거나 작아질 수 있고, 그렇게 된다면 Gradient Descent가 느려질 수 있기 때문에 우리는 작은 값을 선호하는 것이다.
현재 Shallow NN이고, Hidden Unit이 많지 않기 때문에 0.01로 설정하면 적당히 동작을 할 것이다. 다음 심층신경망의 경우에는 0.01과는 다른 상수를 고를 수도 있는데, 4주차 강의에서 다루도록 하겠다.
그리고 파라미터 b에는 대칭 문제가 발생하지 않으므로, 0으로 초기화해도 된다. w가 임의로 초기화되었기 때문에 hidden unit은 각각 다른 값들로 계산되고, symetry breaking 문제는 없게된다. 계속해서 마찬가지로 \(W^{[2]}\)도 유사하게 랜덤으로 초기화를 진행하고, \(b^{[2]}\) 또한 0으로 초기화해도 된다.
'Coursera 강의 > Deep Learning' 카테고리의 다른 글
| [실습] Logistic Regression with a Neural Network(can / non-cat classifier) (0) | 2020.09.24 |
|---|---|
| Practical aspects of Deep Learning 2 (3) | 2020.09.23 |
| Practical aspects of Deep Learning 1 (1) | 2020.09.23 |
| Deep Neural Network(DNN) (0) | 2020.09.20 |
| Basics of Neural Network programming (Week 1, 2) (3) | 2020.08.30 |




댓글