해당 내용은 Coursera의 딥러닝 특화과정(Deep Learning Specialization)의 두 번째 강의 Improving Deep Neural Networks: Hyperparameter tuning, Regularization and Optimization를 듣고 정리한 내용입니다. (Week 1)
이어서 optimization problem을 설정하는 것에 대해서 알아보자.
- Setting up your optimization problem
[Normalizing inputs]
학습속도를 높일 수 있는 방법 중 하나가 입력을 표준화(Normalization)하는 것이다.
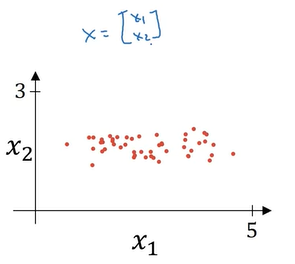
두 개의 input이 있는 경우를 살펴보도록하자.
입력을 normalization 하는 방법은 다음과 같이 두 단계로 이루어진다.
1. 평균을 빼거나, 0으로 만드는 방법
\[\mu = \frac{1}{m}\sum_{i = 1}^{m}x^{(i)}\]
위와 같이 평균 \(\mu\)를 구해서 x에 이 값을 빼준다.
\[x := x - \mu\]
이 과정을 거치면, 다음과 같이 그래프가 이동한다.

2. Normalize variance
\[\sigma^2 = \frac{1}{m}\sum_{i = 1}^{m}(x^{(i)})^2\]
분산 \(\sigma^2\)를 구해서 표준편차 \(\sigma\)를 x에 나누어 준다.
\[x /= \sigma\]
즉, 다음과 같이 normalization된다.
\[\frac{x - \mu}{\sigma}\]
이렇게 normalization해주게 되면, 그래프로는 다음과 같이 나오며 x1과 x2의 편차가 모두 1이 된다.
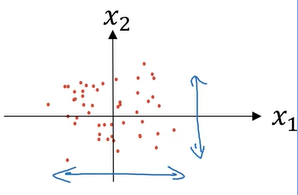
만약 이 방법을 사용해서 training set에 적용할 것이라면, 똑같은 \(\mu, \sigma\)를 test set에 적용해야한다.
training set과 test set을 다르게 normalization하는 것은 좋지 않다.
Why normalize inputs?
\(J(w, b) = \frac{1}{m}\sum\mathscr{L}(\hat{y}^{(i)}, y^{(i)})\)
표준화 되지 않은 input feature를 사용하게 되면, 아래와 같은 J 그래프를 얻을 수 있다.
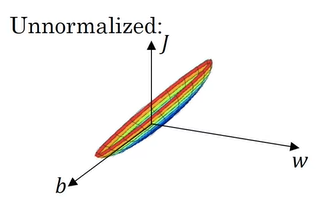
만약 x1의 범위가 1~1000이고, x2의 범위가 0~1이라면, w1과 w2의 범위가 매우 다른 값을 띄게 될 것이다.
그래서 위와 같은 그래프가 나오게 될 것이고, 위 그래프의 contour를 그려보면, 다음과 같다.

feature를 normalization하면, Cost Function은 평균적으로 더 대칭적인 성향을 띄게 되고, 그래프와 contour는 다음과 같을 것이다.

만약 normalization되지 않은 feature를 사용한다면, 매우 작은 learning rate를 사용해야 된다. 왜냐하면 Gradient Descent 를 수행하면 더 많은 단계를 거쳐서 최소값에 도달하기까지 계속 왔다갔다 할 수 있기 때문이다.

만약 normalization을 사용해서 더 구형의 contour를 띄고 있다면, 어디서 시작하더라도 Gradient Descent가 바로 최소값에 도달할 수 있다.

물론 실제로는 파라미터 W가 고차원의 matrix이기 때문에 그래프로 나타내기는 힘들어서 정확하게 전달되지 않는 부분도 있지만, 주로 Cost Function은 더 구형이 띄고, feature를 유사한 scale로 맞추게 되면 더 쉽게 최적화할 수 있다.
만약 x1이 0~1의 범위를 갖고, x2가 -1~1의 범위를 갖고, x3가 1~2의 범위를 갖는다면, 이 feautre들은 서로 비슷한 범위에 있기 때문에 실제로 잘 동작한다.
범위가 크게 다를 때가 문제인데, 이런 경우에 평균을 0으로 만들고, 분산을 1로 만든다면 학습이 더 빨라질 수 있다.
[Vanishing / Exploding gradients]
DNN을 학습할 때, 가장 큰 문제점 중에 하나는 Gradient가 매우 작아지거나 증가하는 경우이다.
이것은 신경망의 미분항이나 기울기가 매우 커지거나 작아진다는 것을 의미한다. 이런 경우에는 학습이 매우 까다로울 수 있다.
이번에 Vanishing/Exploding gradient의 문제점이 무엇인지 살펴보고, random weight initialization을 통해서 이 문제를 줄이는 것을 살펴보자.

다음과 같이 unit의 수는 작지만(ppt에 표현하기 힘들기 때문에), 매우 deep한 NN을 살펴보자.
그리고 activation function은 \(g(z) = z\)로 linear하며, 파라미터 b=0으로 무시한다.
이런 경우 결과값은
\(y = W^{[L]}W^{[L-1]}W^{[L-2]}\cdots W^{[3]}W^{[2]}W^{[1]}x\)
가 될 것이다.
여기서
\(z^{[1]} = W^{[1]}x\)
\(a^{[1]} = g(z^{[1]}) = z^{[1]}\)
\(a^{[2]} = g(z^{[2]}) = g(W^{[2]}a^{[1]})\)
...
\(\hat{y} = \cdots\)
가 된다.
만약 \(W^{[l]}\)의 값이 1보다 약간 큰 \(W^{[l]} = \begin{bmatrix} 1.5 && 0 \\ 0 && 1.5 \end{bmatrix}\) 라고 한다면, 결과값은 다음과 같을 것이다.
\[\hat{y} = W^{[L]} {\begin{bmatrix} 1.5 && 0 \\ 0 && 1.5 \end{bmatrix}}^{L-1}x\]
결국 결과값에 \(1.5^L\)이 곱해지므로, 매우 deep한 NN일 경우에는 결과값 \(\hat{y}\)가 기하급수적으로 증가할 것이다.
반대로 1.5를 0.5로 변경하게 되면, \(0.5^L\)이 되어서 결과값은 매우 작은 값이 될 수 있다.
결과적으로 W의 비중(I Matrix보다 크거나 작은 경우에)에 따라서, activation unit이 매우 커지거나 작아질 수 있다는 것이다.
여기서는 선형 네트워크에서 L에 따라서 결과값이 기하급수적으로 증가하거나 감소하는 것을 예시로 들고 있지만, 비슷하게 기울기값 또한 L에 따라서 기하급수적으로 증가하거나 감소하는 것을 보여줄 수 있다.
기울기가 매우 작거나 크다면, 학습이 어렵다. 특히, 기울기가 매우 작으면 Gradient Descent에 많은 시간이 걸려서 학습이 오래 걸리게 된다.
[Weight Initialization for Deep Networks]
위와 같은 Vanishing/Exploding Gradient 문제를 해결하기 위해서 완전하지는 않지만, random 초기화를 잘하면 어느 정도 문제를 해결할 수 있다.
하나의 Neuron에서의 예시를 먼저 살펴보고, Neural Network로 확장시켜 보자.

어느 layer에서 입력 feature의 수가 n개라면 z는 위와 같이 나타낼 수 있다.(b는 생략)
이런 경우에 적절한 z값을 갖기 위해서 n이 많을 수록, w는 더 작아져야 한다.
이것을 위해서 한 가지 방법은 \(w_i\)을 \(\frac{1}{n}\)으로 두는 것이다.
Var(\(w_i\)) = \(\frac{1}{n}\)
코드상에서는 특정 layer에서 다음과 같이 랜덤 초기화를 할 수 있다.
\(W^{[l]}\) = np.random.randn(shape) * np.sqrt(\(\frac{1}{n^{[l - 1]}}\))
만약 activation function으로 ReLU를 쓰는 경우에는 \(\frac{1}{n}\)이 아닌 \(\frac{2}{n}\)을 사용하는 것이 더 잘 동작한다.(Var(\(w_i\)) = \(\frac{2}{n}\))
이렇게 표준정규분포로 랜덤 초기화를 하고 np.sqrt(\(\frac{1}{n^{[l - 1]}}\))을 곱하는 것이 w의 분산을 \(\frac{1}{n}\)로 만드는 것이다.
activation function에 따라 분산은 다르게 설정될 수 있다.
- tanh를 사용하는 경우.
분산으로 \(\sqrt{\frac{1}{n^{[l-1]}}}\)를 사용하는 것이 잘 동작한다.(Xavier initialization이라고 부른다)
- Yousha Benigo 외 연구진들이 연구한 것
분산으로 \(\sqrt{\frac{2}{n^{[l-1]} + n^{[l]}}}\)을 사용
위 방법들은 w의 분산(편차값)의 기본값을 제시한다. 따라서 분산이 하이퍼파라미터일 수 있다.(선호도는 낮다)
[Numerical approximation of gradients]
BP를 사용하는 경우에 Gradient Checking이라는 테스트를 통해서 BP의 과정이 올바른지 확인할 수 있다.
우선 산술적을 기울기의 값을 구하는 방법부터 알아보자.

위와 같은 그래프를 같는 \(f(\theta)\) 함수의 기울기를 구해보자. 이때 구하는 지점은 \(\theta = 1\)이다. 그리고 \(\epsilon\)값을 0.01로 두고 \(\theta\)값에서 뺴고 더한다.
여기서 산술적으로 \(\theta\)에서의 기울기를 구할 것인데, 작은 삼각형(1 ~ 1.01사이)으로 구하는 것보다 큰 삼각형(0.99~1.01사이)를 사용해서 구하는 것이 더 정확하다.
높이를 너비로 나누어서 기울기를 구하는데 다음과 같이 기울기의 근사치를 구할 수 있다.
\[\frac{f(\theta + \epsilon) - f(\theta - \epsilon)}{2\epsilon} \approx g(\theta)\]
위 값을 구하게 되면, 3.0001이 나온다.
\({f}'(\theta) = g(\theta) = 3\theta^2\)
f의 미분은 다음과 같고, 1에서의 미분값은 3이기 때문에 실제 미분항과 산술적으로 구한 기울기의 오차는 0.0001 이다.
만약 작은 삼각형의 기울기(one-sided difference)를 구하게 되면,
\[\frac{f(\theta + \epsilon) - f(\theta)}{\epsilon}\]
이며, 계산값은 3.0301로, 미분값과 0.0301의 오차를 가지게 된다.
따라서 미분값의 근사치는 two-sided difference(큰 삼각형)이 미분값과 더 유사해서 더 정확도가 높다.
번외로 미분학에서 기울기는 다음과 같이 구한다.
\[{f}'(\theta) = \lim_{\epsilon \rightarrow 0}\frac{f(\theta + \epsilon) - f(\theta - \epsilon)}{2\epsilon}\]
[Gradient Checking]
Gradient Checking은 BP를 사용할 때, 버그를 찾아줌으로써 문제점을 해결하는데 시간을 절약해준다.
어떻게 Gradient Checking을 적용하는지 살펴보자.

1. 모든 파라미터를 벡터로 변환 후에 연결시켜서 big vector로 만들어 준다.
2. dW, db를 d\(\theta\)로 만들어서 \(J(\theta)\)의 기울기와 비교한다.

Gradient Checking은 실질적으로 위와 같이 이루어진다.
각 i마다 기울기의 근사치를 위의 식으로 구한다.
그리고 BP를 통해서 구한 d\(\theta\)와 비교하는데, 비교는 다음과 같은 식으로 값을 구해서 비교한다.
\[\frac{\| d\theta_{\text{approx}} - d\theta \|_2}{\| d\theta_{\text{approx}}\|_2 + \| d\theta \|_2}\]
이때 비교값은 \(\epsilon = 10^{-7}\)로 설정하며, 이 값은 기울기 근사치를 구할 때의 \(\epsilon\)이랑 관련은 없다.
그래서 비교값보다 작으면 훌륭한 결과이고, 만약 \(10^{-5}\)의 값을 가지게 된다면, 나름 괜찮은 결과지만 다시 살펴볼 필요가 있고, \(10^{-3}\)으로 크다면 다시 점검이 필요하다는 것을 의미한다.
즉, \(\epsilon\) 만큼의 값이 나오거나 더 작은 값이 나온다면 BP의 과정이 정상이라는 것이다.
[Gradient Checking Implementation Notes]
Gradient Checking을 사용할 때의 Tip
1. Don't use in training - only to debug
모든 i에 대해서 기울기 근사치를 구하는 것은 계산 시간이 매우 오래 걸린다. 따라서 디버깅할 때만 사용하고, 만약 충분히 오차가 작은값이 나온다면 Gradient Checking은 끄는 것이 좋다.
2. If algorithm fails grad check, look at components to try to identify bug
만약 알고리즘이 Gradient Check에 실패하면, 값이 크게 다른 i를 찾아서 어느 layer에서 버그가 발생하는지 찾을 수 있다. -> 항상은 아니지만 버그를 트래킹할 수 있음
3. Remember regularization
Regularization 항이 있다면 d\(\theta\)에도 추가해야한다.

4. Doesn't work with dropout
dropout에서는 unit을 임의로 제거(J가 제대로 정의되지 않음)하기 때문에, Gradient Checking은 dropout에서는 동작하지 않는다.
5. Run at random initialization; perhaps again after some training
자주 사용하지는 않지만, 파라미터가 0에 가까울 때, Gradient Descent가 잘 동작할 수도 있다. 하지만, Gradient Descent를 진행하면서 파라미터 W, b가 커지면, BP는 오직 W와 b가 0에 가까울 때만 잘 동작할 수 있고, W와 b의 값이 커질수록 정확도가 떨어지게 되는 것이다. 여기서 한 가지 할 수 있는 방법은 Gradient Checking을 random initialization에서 실행시키고, 어느 정도 네트워크 학습을 진행하고, 다시 Gradient Checking을 실행하는 것이다.
'Coursera 강의 > Deep Learning' 카테고리의 다른 글
| [실습] Planar data classification with a hidden layer (9) | 2020.09.25 |
|---|---|
| [실습] Logistic Regression with a Neural Network(can / non-cat classifier) (0) | 2020.09.24 |
| Practical aspects of Deep Learning 1 (1) | 2020.09.23 |
| Deep Neural Network(DNN) (0) | 2020.09.20 |
| Shallow Neural Networks (8) | 2020.09.08 |




댓글