해당 내용은 Coursera의 딥러닝 특화과정(Deep Learning Specialization)의 첫 번째 강의 Neural Networks and Deep Learning를 듣고 정리한 내용입니다. (Week 4)
- Deep L-layer neural network

Deep Learning, Deep Neural Network(DNN)을 알아보기 위해서 위의 사진을 살펴보자.
왼쪽 위는 Logistic Regression이고 오른쪽 위는 1개의 Hidden Layer로 이루어진 NN이다. 이러한 모델을 'Shallow'한 모델이라고 표현한다. 반면에 오른쪽 아래와 같이 5개의 Hidden Layer로 이루어진 NN을 'Deep'한 모델이라고 표현한다. 차이는 Hidden Layer의 차이밖에 없다.
전 강의에서 말했지만, 기억해둘 것은 일반적으로 신경망의 layer를 셀 때, Input Layer는 세지 않는다는 것이다.
[Deep Neural Network Notation]
다음으로 DNN을 나타내는 표기법에 대해서 알아보자.

위와 같은 4-Layer NN일 때, 각 Layer에 대한 표기는 아래와 같다.
- \(L = 4\) : Number of total layer
- \(n^{[l]}\) : Number of units of layer \(l\)
- \(a^{[l]}\) : Activations of layer \(l\) -> \(a^{[l]} = g^{[l]}(z^{[l]})\)
- \(w^{[l]}\) : Weights for \(z^{[l]}\)
- \(b^{[l]}\) : Bias parameter for \(z^{[l]}\)
Input Layer는 0번째 layer라고 볼 수 있으며, 입력 x는 \(a^{[0]}\)으로 나타낼 수 있다. 출력은 \(\hat{y}\)로 \(a^{[L]}\)으로 나타낼 수 있다. 위의 DNN인 경우에 layer의 units은 아래와 같이 나타낼 수 있다.
\[n^{[1]} = 5, n^{[2]} = 5, n^{[3]} = 3, n^{[4]} = 1, n^{[0]} = n_x = 3\]
[Forward Propagation in a DNN]

위와 같은 DNN이 있을 때, 한 개의 example에 대한 FP를 살펴보자.
우선 1,2,4 Layer에서의 계산은 다음과 같다. 여기서 \(a^{[0]} = x\)이다.
\[\begin{align*} z^{[1]} &= w^{[1]}a^{[0]} + b^{[1]} \\ a^{[1]} &= g^{[1]}(z^{[1]}) \\ z^{[2]} &= w^{[2]}a^{[1]} + b^{[2]} \\ a^{[2]} &= g^{[2]}(z^{[2]}) \\ z^{[4]} &= w^{[4]}a^{[3]} + b^{[4]} \\ a^{[4]} &= g^{[4]}(z^{[4]}) = \hat{y} \end{align*}\]
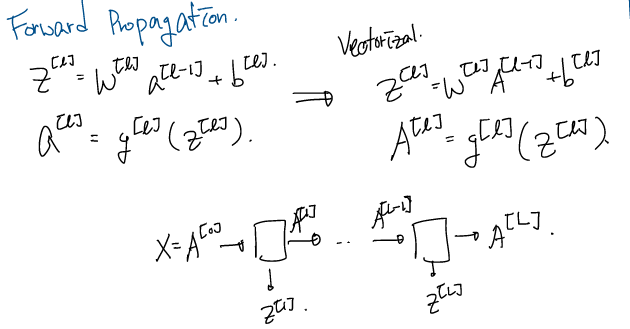
즉, 일반화를 하면 다음과 같다.
\[\begin{align*} z^{[l]} &= w^{[l]}a^{[l-1]} + b^{[l]} \\ a^{[l]} &= g^{[l]}(z^{[l]}) \end{align*}\]
그리고, 모든 training example에 대해서 벡터화를 하여서 표현하게 되면 아래와 같다.
\[\begin{align*} Z^{[1]} &= W^{[1]}A^{[0]} + b^{[1]} \\ A^{[1]} &= g^{[1]}(Z^{[1]}) \\ Z^{[2]} &= W^{[2]}A^{[1]} + b^{[2]} \\ A^{[2]} &= g^{[2]}(Z^{[2]}) \\ \hat{y} &= g^{[4]}(Z^{[4]}) = A^{[4]} \end{align*}\]
일반화는 한 개의 example과 동일하고, 대문자로 표기한다.
\[\begin{align*} Z^{[l]} &= W^{[l]}A^{[l-1]} + b^{[l]} \\ A^{[l]} &= g^{[l]}(Z^{[l]}) \end{align*}\]
\(X = A^{[0]}\)이며, Z는 모든 training example에 대해서 다음과 같이 나타낸다.
\[Z^{[l]} = \begin{bmatrix} | & | & & | \\ z^{[l](1)} & z^{[l](2)} & \cdots & z^{[l](m)} \\ | & | & & | \end{bmatrix}\]
1-layer에서 반복문을 피해서 벡터화하여 연산을 진행했지만, 각 레이어는 반복문을 쓰는 것 말고는 방법이 없다. 따라서, FP를 수행할 때, 각 Layer에 대해서 반복문을 수행해야 한다. 이때는 특히 각 Matrix의 차원을 조심해야 한다.
[Getting Matrix Dimension Right]
DNN을 수행할 때, 각 파라미터에 대한 행렬 차원을 유의해야한다.

DNN에서 파라미터 \(W^{[l]}, b^{[l]}\)의 차원은 다음과 같다. 각 파라미터의 미분항은 파라미터의 차원과 동일하다.
\[\begin{align*} W^{[l]} &: (n^{[l]}, n^{[l-1]}) \\ b^{[l]} &: (n^{[l]}, 1) \\ dW^{[l]} &: (n^{[l]}, n^{[l-1]}) \\ db^{[l]} &: (n^{[l]}, 1) \end{align*}\]
그래서 모든 example training에 대한 계산을 위해 벡터화하여 연산을 하면 다음과 같이 된다.

일반화하면 다음과 같다.
- \(z^{[l]}, a^{[l]} : (n^{[l]}, 1)\)
- \(Z^{[l]}, A^{[l]} : (n^{[l]}, m)\), if \(l = 0\), \(A^{[0]} = X : (n^{[0]}, m)\)
- \(dZ^{[l]}, dA^{[l]} : (n^{[l]}, m)\)
버그 감소를 위해서 Dimension이 일관적으로 유지하는 것이 중요하다.
[Why deep representations ?]
DNN은 여러가지 문제에서 잘 동작하는데, 단순히 신경망의 크기가 크기만해서 잘 동작하는 것은 아니다. 신경망이 깊고, 숨겨진 layer가 많아야 한다. 몇 개의 예제를 통해서 살펴보자.

위와 같은 얼굴인식 또는 얼굴감시 시스템을 구현할 때, DNN이 하는 동작은 다음과 같다.
얼굴 사진을 입력했을 때, 첫 번째 layer는 feature detector 또는 edge detector 일 수 있다. 위 예제는 입력된 이미지에서 20개의 hidden layer를 통해서 DNN이 계산하는 것을 나타낸 것이고, 아래 사각형의 박스로 hidden unit을 시각화했다. 첫 번째 층에서 hidden unit은 이미지 모서리가 어딘지 파악한다. (나중에 CNN에 대해서 배우게 되면 더 이해가 빠를 것이다.), 그리고 파악된 모서시들을 그룹으로 묶어서, 얼굴의 일부를 만들어 나가게 되는데, 모서리들을 취합하는 과정에서 얼굴의 다른 부분들을 감지할 수 있는 것이다. 그리고 최종적으로 여러 얼굴 부위들을 합치게 된다.
즉, 초기의 layer에서는 간단한 모서리와 같은 함수를 감지하는 것이고, 다음 단계의 layer에서 이런 내용들을 취합해서 더욱 복잡한 함수를 배운다.
얼굴 인식 분야외에도 음성 인식 시스템도 동일하다. 음성을 시각화하는 것이 쉽지는 않지만, 이 시스템의 첫 번째 layer에서는 low level wave form을 감지하도록 학습할 수 있다(백색소음인지 등). 그리고 이러한 정보를 취합하여 기본적인 음성 unit(phoneme)을 감지할 수 있다.
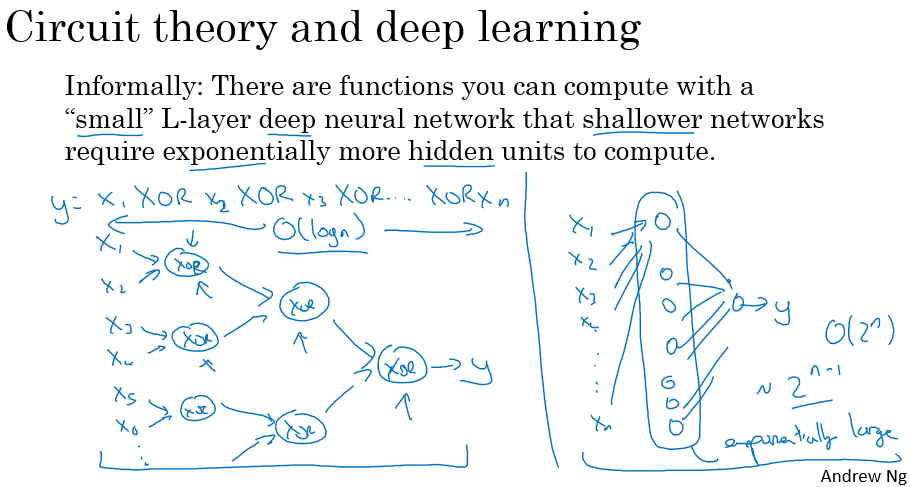
그리고, Circuit theory에서 유래된 결과를 살펴보자.
우리가 만약 \(x_1\) XOR \(x_2\) XOR \(x3\) XOR \(\cdots x_n\)을 계산하려고 한다면, 왼쪽 경우처럼 XOR Tree를 그려가면서 최종적인 결과 \(y\)를 구할 수 있을 것이다(엄밀히 이야기하면 XOR를 계산하는데 AND와 NOT게이트를 이용해 2개의 layer로 XOR을 구할 수 있다). 여기서 XOR을 계산하기 위한 네트워크의 깊이는 \(logN\)이 될 것이다.
하지만 오른쪽 경우와 같이 hidden layer가 하나만 존재할 경우에는 \(2^N\)개의 입력의 XOR을 계산하기 위해서 hidden layer가 매우 커야하고, 연산이 커져서 느려질 수 있다.
[Building blocks of deep neural networks]
우리는 이전에 DNN을 구성할 때, 핵심 요소인 Forward/Backward Propagation의 기본을 이미 배웠고, 이것을 하나로 합쳐서 어떻게 Deep Network를 구성하는지 살펴보자. 여기 4개의 Layer로 구성된 DNN이 있을 때, 한 Layer에서 FP와 BP는 다음과 같이 계산된다.

- FP : Input \(a^{[l-1]}\), Output \(a^{[l]}\), Cache \(z^{[l]}\)
(\(z^{[l]} = W^{[l]}a^{[l-1]} + b^{[l]}\), \(a^{[l]} = g^{[l]}(z^{[l]})\))
- BP : Input \(da^{[l]}\), Ouput \(da^{[l-1]}, dw^{[l]}, db^{[[l]}\)
여기서 cache는 FP에서 계산한 \(z^{[l]}\)이 BP에서 \(dz^{[l]}\)을 구하는데 다시 사용되기 때문에 저장해놓은 것을 의미한다.
요약을 하자면 다음과 같이 나타낼 수 있다.

위를 토대로 전체 DNN에서의 과정을 요약하면 다음과 같다.

이렇게 FP와 BP를 통해서 \(dw^{[l]}\)와 \(db^{[l]}\)을 구해서, \(w, b\)를 갱신하게 된다.
\[\begin{matrix} w^{[l]} = w^{[l]} - \alpha dw^{[l]} \\ b^{[l]} = b^{[l]} - \alpha db^{[l]} \end{matrix}\]
그리고 계속 언급하고 있지만, 반복문을 감소시켜 연산을 빠르게 하기 위해서 벡터화해서 FP와 BP를 계산하면 다음과 같이 계산할 수 있다.

전체 과정을 요약하면, X를 입력으로 중간에 존재하는 hidden layer는 activation function으로 ReLU가 될 것이고, 마지막 Output layer는 Sigmoid가 될 것이고, FP를 통해서 \(\hat{y}\)를 구한다. 그리고 이 값으로 Loss를 산출하고, BP를 통해서 미분항들을 산출하게 된다.
여기서 FP의 경우에는 입력 \(X\)로 초기화되어서 계산되고, BP의 경우에는 \(dA^{[L]}\)을 초기값으로 계산된다.

[Parameters vs Hyperparameters]
우리가 NN을 효과적으로 동작시키기 위해서는 Parameter뿐만아니라 Hyperparameter(하이퍼파라미터) 또한 잘 구성해야한다.
여기서 우선 Hyperparameter가 무엇인지 살펴보자.
머신러닝 모델에서 파라미터는 \(W\)와 \(b\)이다. 그리고 알고리즘에서 우리가 설정해주어야하는 값이 있는데, Learning Rate인 \(\alpha\)와 같은 값이 있고, 알고리즘에서 진행되는 iteration이나 Hidden Layer의 개수를 알려줘야 하기도 한다. 추가적으로 activation function으로 어떤 함수를 어떤 것으로 사용할지에 대한 선택도 있다(ReLU, Sigmoid, tanh 등). 이러한 것들이 궁극적으로 \(W, b\)를 컨트롤하기 때문에 Hyperparameter라고 한다.
Hyperparameters
- Learning Rate \(\alpha\)
- Number of iterations
- Number of hidden layer \(L\)
- Number of hidden unit \(n^{[1]}, n^{[2]}, \cdots\)
- Choice of activation function
사실 가장 좋은 hyperparameter 값이 어떤 것인지 미리 알아내는 것은 매우 어렵다. 그래서 딥러닝을 적용할 때, 우리는 아래와 같이 다양한 아이디어를 가지고 시도해보고 그 결과를 바탕으로 다시 하이퍼 파라미터 값들을 변경해서 다시 시도해보는 방법 밖에 없다.

'Empirical Process'는 여러 가지 방법을 시도해보고 어떤 것이 잘 동작하는지 확인하는 것을 표현한 것이다.
그리고, 어느 한 가지 분야에서 오랫동안 있었다면 가장 최적의 값이 정해져 있을 수도 있는데, 이 최적의 값은 변할 수 있다. 즉, 오늘 가장 최적의 하이퍼파라미터로 시스템을 튜닝한다고 하더라도, 1년 후에는 이 값이 최적이 아닐 수도 있다는 것이다. 컴퓨터 인프라나, CPU/GPU 같은 것들이 완전히 변해서 그럴 수도 있다.
그래서, 먼저 몇 개의 값으로 시도해보고, 더 좋은 값이 있는지 확인해보는게 최선이고, 이렇게 진행하다보면 하이퍼 파라미터에 대한 직관적인 이해도가 늘어나서 본인의 문제에 어떤 것이 가장 적합한지 배울 수 있을 것이다.
'Coursera 강의 > Deep Learning' 카테고리의 다른 글
| [실습] Logistic Regression with a Neural Network(can / non-cat classifier) (0) | 2020.09.24 |
|---|---|
| Practical aspects of Deep Learning 2 (3) | 2020.09.23 |
| Practical aspects of Deep Learning 1 (1) | 2020.09.23 |
| Shallow Neural Networks (8) | 2020.09.08 |
| Basics of Neural Network programming (Week 1, 2) (3) | 2020.08.30 |




댓글