[Machine Learning] Support Vector Machine

해당 내용은 Andrew Ng 교수님의 Machine Learning 강의(Coursera)를 정리한 내용입니다.

 

이때까지 여러 종류의 학습 알고리즘에 대해서 알아보았다. Supervised learning에서 대부분의 학습 알고리즘의 성능은 유사하고, 우리에게는 어떤 알고리즘을 선택하느냐가 아니라 학습 알고리즘에 얼마나 많은 data를 적용할 것이냐가 문제가 될 것이다. Logistic Regression이나 Neural Network랑 비교했을때, Support Vector Machine(SVM)은 복잡한 비선형 함수에 대해서 때때로 더욱 명확하고 강력한 학습 알고리즘이 될 수 있다. 

 

- Optimization objective

SVM을 알아보기 전에 Logistic Regression을 다시 살펴보자.

 

 

 

 

Logistic Regression의 Hypothesis Function(예측 함수, 가설 함수)와 그래프는 위와 같다.

• If \(y = 1\), we want \(h_\theta(x) \approx 1\), \(\theta^Tx \gg 0\)
• If \(y = 0\), we want \(h_\theta(x) \approx 0\), \(\theta^Tx \ll 0\)

여기서 우리는 \(y = 1\)일 때, \(\theta^Tx \gg 0\)을 만들어주는 \(\theta\)를, \(y = 0\)일 때, \(\theta^Tx \ll 0\)을 만들어주는 \(\theta\)를 찾는 것이 목적이다.

 

한 개의 Training example (x, y)에 대한 Cost Function에 대해서 살펴보자.

Cost of example: \(-(ylogh_\theta(x) + (1 - y)log(1 - h_\theta(x))\)

\[= -ylog\frac{1}{1 + e^{-\theta^Tx}} - (1 - y)log(1 - \frac{1}{1 + e^{-\theta^Tx}})\]

 

여기서 \(y = 1\), (\(\text{want }\theta^Tx \gg 0\)) 경우에 그래프는 다음과 같이 나타낼 수 있다.

 

 

 

 

y의 값이 1이기 때문에, Cost에서 첫 번째 항 \(-ylog\frac{1}{1 + e^{-\theta^Tx}}\)만 고려된다. 따라서 z, 즉 \(\theta^Tx\)가 클수록 대응대는 값은 0에 가까워진다.

이제, 우리는 SVM에서는 그래프이 보라색 선과 같이 표현할 것이다(log를 사용하지 않고 직선으로 나타낼 것이다). 1을 기준으로 1보다 크다면 flat하며, 1보다 작으면 점점 증가하는 직선으로 그려서, 부분적인 직선(piecewise-linear)으로 나타낼 것이다. 증가하는 직선에서 기울기는 중요하지 않으며, 이렇게 Logistic Regression과 유사한 직선을 새롭게 나타냄으로써 우리는 SVM에서 계산상의 이점을 갖게되고, 나중에 문제를 더 쉽게 최적화할 수 있을 것이다.

 

 

 

 

y의 값이 0일 때에는 반대로 그려지며, 이때 -1을 기준으로 부분적인 직선이 그려진다.

(\(- (1 - y)log(1 - \frac{1}{1 + e^{-\theta^Tx}})\))

※ 이렇게 piecewise-linear한 함수를 hinge loss function이라고 부른다.

 

이때, \(y = 1\)일 때의 cost를 \(cost_1(z)\)라고 표현하고, \(y = 0\)일 때의 cost를 \(cost_0(z)\)라고 나타낸다.

 

[Cost Function]

따라서 Logistic Regression의 Cost Function에서 새롭게 정의한 \(cost_1(z), cost_0(z)\)를 대입해서 새롭게 SVM Cost Function을 정의한다.

 

 

 

 

기존 logistic regression의 Cost Function에서 1)Cost최적화에 상관이 없는 Training Example의 개수인 m이 제거되고, 2)새롭게 정의한 cost함수(hinge loss function)을 대입하고, 3)Regularization Parameter \(\lambda\)를 제거하고 첫 번째항에 C라는 parameter를 추가하였다.

이때, C는 \(\frac{1}{\lambda}\)이다. 첫번째 항을 A, 두번째 항을 B라고 둔다면 \(CA + B\)로 나타낼 수 있다.

\(\lambda\)를 제거하고 C를 사용하는 이유는 SVM에서 편의성을 위해서이다.

 

정리하면 다음과 같다.

 

 

 

 

[SVM Hypothesis]

SVM의 Hypothesis Function은 다음과 같다. y가 1이거나 0일 확률로 계산하지 않으며, Hypothesis Function의 결과값은 0 또는 1으로 명확하다.

\[h_\theta(x) = \left\{\begin{matrix} 1\text{      }\text{if } \theta^Tx \gg 0 \\  0\text{      }\text{if } \theta^Tx \ll 0 \end{matrix}\right.\]

 

 

- Large Margin Intuition

SVM은 Large Margin Classifier이라고 불린다. 이번에는 SVM이 왜 이렇게 불리는지, SVM의 hypothesis가 어떻게 나타나는지 보면서 알아보자.

 

 

 

 

 

SVM의 Cost Function은 위와 같다. 여기서 z가 1보다 클 때만 \(cost_1(z)\)가 0이고, z가 -1보다 작을 때만 \(cost_0(z)\)가 0이다. Logistic Regression(LR)에서는 0이 기준이었다.

하지만, SVM에서는 +1 이상일 때와 -1 이하일 때만 Hypothesis의 값을 결정하도록 한다. 이 부분이 SVM에서 extra safety factor or safety margin factor라는 Margin을 설정하게 된다.

 

[SVM Decision Boundary]

 

 

 

 

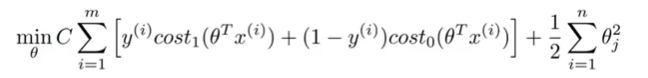
C가 아주 크다고 가정을 해보자. C가 매우 크다면 위 Cost Function을 최적화하는, 즉 Cost Function을 최소화하기 위해서, 첫번째 항인 A가 거의 0에 가까워야 할 것이다. 이때, A가 0이 되는 지점이 바로 SVM의 Decision Boundary가 된다. 

A가 0이되면, 위 최적화 문제는 아래와 같이 단순해진다.

\(\Rightarrow \underset{\theta}{min} \frac{1}{2}\sum_{j = 1}^{n}\theta_j^2\)

s.t. \(\begin{matrix} \theta^Tx^{(i)} \geq 1 & \text{ if } y^{(i)} = 1 \\ \theta^Tx^{(i)} \leq -1 & \text{ if } y^{(i)} = 0 \end{matrix}\)

 

 

 

 

 

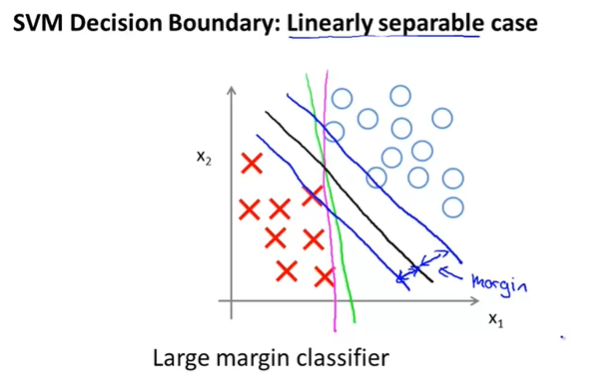
위와 같은 예제에서 다양한 Decision Boundary가 있을 수 있다.

우리는 연두색 그래프와 같이 Decision Boundary를 결정할 수 있지만, 이는 좋은 Decision Boundary로 보이지는 않는다. 더욱 최악의 케이스인 보라색 그래프와 같이 Decision Boundary를 그릴 수도 있다.

 

하지만, SVM을 사용하면 검은색 그래프와 같은 Decision Boundary를 찾게될 것이다. 연두색이나 보라색 그래프보다는 훨씬 좋은 Decision Boundary로 보이며, positive/negative examples을 분류하는데 잘 동작할 것이다. 그리고, 검은색 그래프는 Data examples과 더 큰 Distance를 갖게되며, 이 Distance를 SVM의 Margin이라고 한다.

 

그래서 SVM은 Large Margin Classifier이라고 불리며, SVM은 가능한 큰 Margin으로 Data를 분류하려고 하기 때문에 확실한 견고성(robustness)를 갖는다. 어떻게 SVM이 큰 Margin을 갖게하는지는 잠시 후에 설명하도록 하겠다.

중요한 것은 SVM이 가능한 Large Margin으로 Example들을 분류하려고 한다는 것이다.

 

 

 

 

 

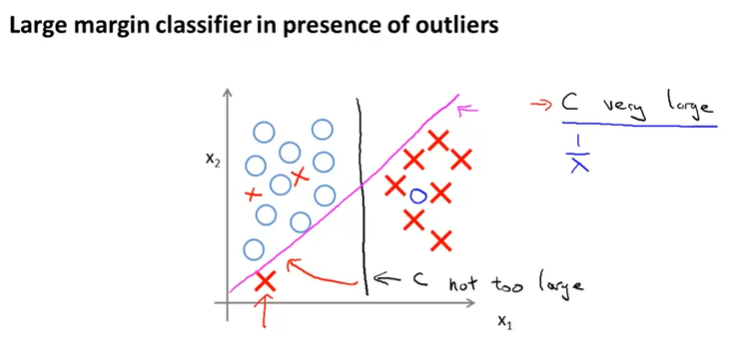
위와 같은 예제(하나의 negative example이 왼쪽 하단에 있을 때)가 있을때, C가 매우 크다면 보라색 그래프와 같은 Decision Boundary를 가질 것이고, C가 크기 않으면 검은색 그래프의 Decision Boundary를 갖게 될 것이다.

C는 regularization 파라미터 \(\lambda\)와 연관이 되어서, 학습 알고리즘에서 Overfitting(과적합)을 조정한다. 즉, C가 매우 크다면 \(\lambda\)가 매우 작다는 의미이고 이는 \(\theta\)가 미치는 영향이 커져서 과적합 확률이 높아진다.

 

outlier는 보통의 data와는 크게 다른 data를 의미한다. 여기서는 왼쪽 아래에 위치하는 negative example을 의미한다.

 

- The mathematics behind large margin classification

SVM이 어떻게 동작하는지 이해하기 위해서 수학적인 내용을 살펴보자.

[Vector Inner Product : 벡터 내적]

 

 

 

 

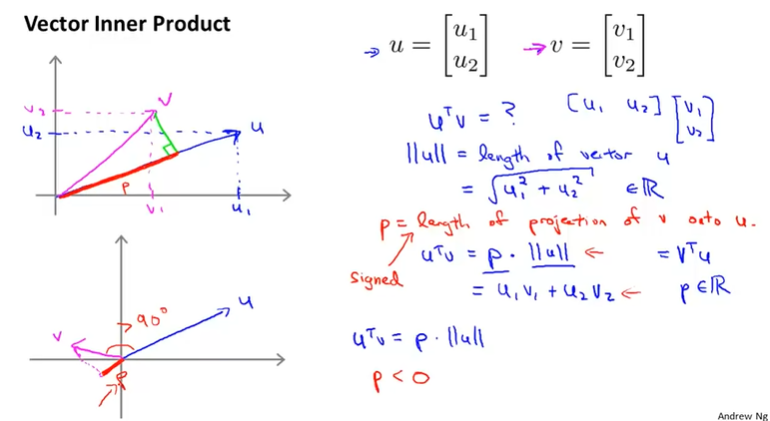
여기서 u와 v 벡터의 내적인 \(u^Tv\)의 의미는 무엇일까?

두 벡터의 내적은 벡터 \(v\)를 벡터 \(u\)에 projection(투영)한 것이고, 이 내적은 다음과 같이 표현할 수 있다.

\[\begin{align*} u^Tv &= p\cdot\ \left \| u \right \| \\  &= u_1v_1 + u_2v_2 \end{align*}\]

이때, \( \left\| u \right\| = \sqrt{u_1^2 + u_2^2}\) 이며, norm이라고 부르고 length of  vector를 의미한다.

\(p\)는 scalar값이며 length of projection of \(v\) and \(u\)를 의미한다. \(p\)는 \(\theta > 90^{\circ}\) 일 때, 음수이다. 

 

[SVM Decision Boundary]

SVM의 Decision Boundary는 아래의 Optimization Problem이다.

\(\underset{\theta}{min} \frac{1}{2}\sum_{j = 1}^{n}\theta_j^2\)

s.t. \(\begin{matrix} \theta^Tx^{(i)} \geq 1 & \text{ if } y^{(i)} = 1 \\ \theta^Tx^{(i)} \leq -1 & \text{ if } y^{(i)} = 0 \end{matrix}\)

 

식의 단순화를 위해서 \(\theta\)은 0으로 두고, n(dimention of features)은 2이라고 가정하고 살펴보자.

위 식은 아래와 같이 나타낼 수 있다.

\[\begin{align*} \frac{1}{2}\sum_{j = 1}^{n}\theta_j^2 &= \frac{1}{2}(\theta_1^2 + \theta_2^2) \\ &= \frac{1}{2}(\sqrt{\theta_1^2 + \theta_2^2})^2 \\ &= \frac{1}{2}\left\| \theta \right\|^2 \end{align*}\]

이때, \(\theta\)는 \(\begin{bmatrix} \theta_1 \\ \theta_2 \end{bmatrix}\)이며, \(\theta_0 = 0\)이다.

 

 

 

 

 

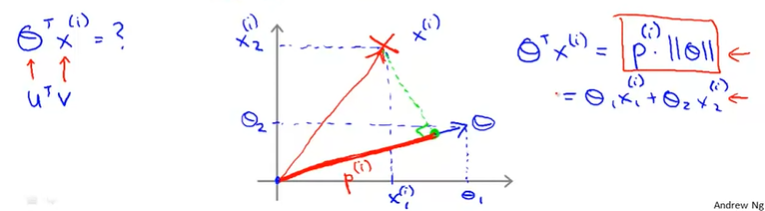
그리고 \(\theta^Tx^{(i)}\) 항은 \(x\) vector를 \(\theta\) vector로 투영시킨 것으로 볼 수 있다. 그래서 다르게 표현하면 다음과 같다.

\[\theta^Tx^{(i)} = p^{(i)}\cdot\ \left \| \theta \right \| = \theta_1x_1^{(i)} + \theta_2x_2^{(i)}\]

즉, \(p^{(i)}\cdot \left \| \theta \right \|\)값이 1보다 커야지 \(y = 1\) 이다.

 

 

 

 

 

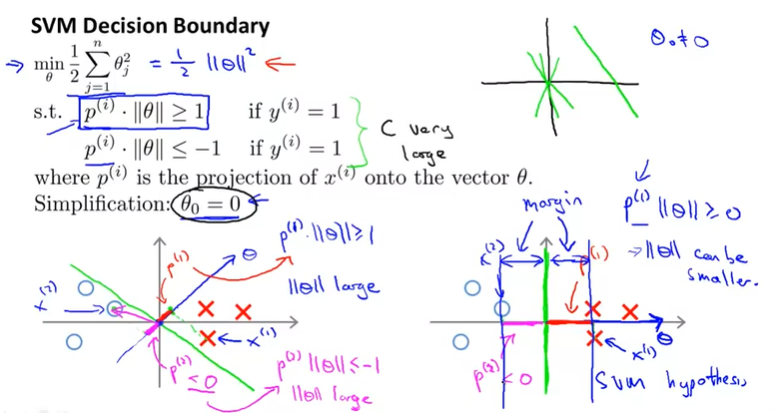
왼쪽 그래프에서 녹색의 Decision Boundary를 살펴보자.

녹색 선에 직교(orthogonal)하는 \(\theta\) vector에 example \(x^{(i)}\)를 투영해보면 거리 \(p^{(i)}\)가 너무 작다. \(p^{(i)}\)가 작다는 것은 \(\left \| \theta \right \|\)가 크다는 의미이므로, Cost Function의 값이 커지는 문제가 발생한다. 

 

반면에 오른쪽 그래프에서는 \(x^{(i)}\)가 투영된 거리 \(p^{(i)}\)가 크다. 즉, \(p^{(i)}\)가 크기 때문에 \(\left \| \theta \right \|\)가 작고, 결과적으로 Cost Function의 값이 작아져서 최적화된다.

 

따라서, SVM을 사용해서 학습 알고리즘을 구현하면 Margin이 큰 Decision Boundary를 찾게되는 것이다.

 

여기에서는 \(\theta_0\)을 0으로 가정하고 살펴보았다. \(\theta_0 = 0\)의 의미는 \(\theta\) vector가 원점을 지난다는 의미이다. 즉, 0이 아니면 단순히 원점을 지나지 않는다는 차이점 밖에 없다.

 

 

 

 

 

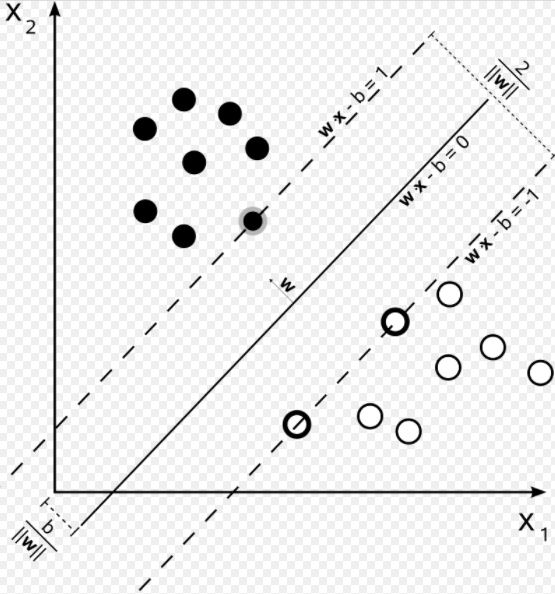
여기서 \(w\)는 parameter \(\theta\)를 의미한다. 여기서 \(w \cdot x - b = 1, w \cdot x - b = 1\)에 해당하는 직선이 support vector이다. Decision Boundary에 해당하는 \(w \cdot x - b = 0\)를 hyperplane(초평면)이라고 하며, Data가 n차원이라면 초평면은 n-1차원이 된다(여기서는 n = 2, 초평면은 1차원).

 

 

+) \(\theta\) vector가 Decision Boundary에 직교하는 이유 ?

\(\theta^Tx = 0\)(if \(\theta_0 = 0\)), 또는 \(\theta^Tx + b\)(if \(\theta_0 \neq 0\))를 만족하는 선이 Decision Boundary이다. 계산상의 편의상으로 b를 0이라고 두면, \(\theta^Tx = 0\)를 구하면 되고, \(\theta\)와 \(x\)의 내적은 \(p\)가 된다. 이때 내적의 값이 0이되는 각도는 90도가 되며, \(x\)의 모든 vector는 \(\theta\) vector에 직교한다는 것을 의미한다.