해당 내용은 Andrew Ng 교수님의 Machine Learning 강의(Coursera)를 정리한 내용입니다.
[Evaluating a Learning Algorithm]
- Deciding what to try next
Debugging a learning algorithm
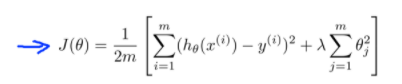
Regularized linear regression을 사용해서 집값을 예측한다고 할 때, 위와 같은 Cost Function이 있다. 하지만, 우리가 새로운 집에 대한 예측을 하는 경우에 큰 에러가 발생한다면, 다음과 같은 방법을 시도할 수 있다.
- Training example을 더 얻는다.
- Feature의 갯수를 줄이거나 늘린다.
- Polynomial features를 추가한다.(\(x_1^2, x_2^2, x_1x_2\), etc..)
- \(\lambda\)를 감소하거나 증가시킨다.
Machine learning diagnostic
하지만 위의 방법들을 무작정 시도하는 것보다는 현재 학습 알고리즘에 어느 부분에 문제가 있는지 진단(diagnostic)을 해서 성능을 높힐 수 있는 가이드를 잡는 것이 효율적이다.
진단하는 것은 실행하는 데 시간이 걸릴 수 있지만, 매우 효율적일 것이다.
- Evaluating a hypothesis

우리가 학습한 알고리즘이 적절한 지 확인할 때, feature가 작다면 함수 그래프를 보면서 파악할 수 있지만, feature의 수가 많고 복잡하다면 다른 방법이 필요하다.

그 방법 중의 하나가 Training Set을 2개의 영역으로 나누어서 Hypothesis Function을 평가하는 것이다. 일부는 Training에 사용되고, 일부는 Test에 사용을 해서 성능을 평가한다. 여기서는 Training Example의 70%는 Training Set으로 가설함수를 학습시키는데 사용하였고, 나머지 30%는 Test Set으로 우리가 학습한 가설함수가 다른 데이터에도 잘 맞는지 판단하는데 사용된다. 새로운 Notation은 위 그림의 오른쪽과 같다.
- Training/testing procedure for linear regression
우선 linear regression에서 순서를 보면 아래와 같다.
1. Learn parameter \(\theta\) from training data(minimizing training error \(J(\theta)\))
2. Compute test set error \(J_{test}(\theta)\)
$$J_{test}(\theta) = \frac{1}{2m_{test}}\sum_{i = 1}^{m_{test}}(h_\theta(x_{test}^{(i)}) - y_{test}^{(i)})^2$$
먼저 전체 70%인 Training Set으로부터 \(\theta\)를 학습시킨다. 즉, Training Error \(J(\theta)\)를 최소화시킬 것이다. 그리고 30%인 Test Set으로 Test Set Error를 계산한다. 만약 Test Set Error가 Training Error에 비해서 크다면, 성능이 좋지 않다는 것으로 판단할 수 있다.
예를 들어, Overfitting의 경우에는 Training Error는 매우 작고, Test Error는 매우 클 것이다.
- Trainig/testing procedure for logistic regression
logistic regression에서도 대부분 동일하며, error를 구하는 공식이 다르다.
1. Learn parameter \(\theta\) from training data
2. Compute test set error \(J_{test}(\theta)\)
$$J_{test}(\theta) = -\frac{1}{m_{test}}\sum_{i = 1}^{m_{test}} \left [y_{test}^{(i)}log(h_\theta(x_{test}^{(i)})) + (1 - y_{test}^{(i)})log(1 - h_\theta(x_{test}^{(i)}))\right ]$$
Binary Classification 문제의 경우에는 output이 1 또는 0이며 이런 상황의 Error를 Misclassification error라 일컷는다.
이때, Error는 다음과 같이 구할 수 있다.
$$err(h_\theta(x), y) = \left\{\begin{matrix} 1 \text{ if } h_\theta(x) \leq 0.5 \text{ and } y = 0 \text{ or } h_\theta(x) < 0.5 \text{ and } y = 1 \\ 0 \text{ otherwise } \end{matrix}\right.$$
즉, Test Error는 다음과 같다.
$$\text{Test error } = \frac{1}{m_{test}}\sum_{i = 1}^{m_{test}}err(h_\theta(x_{test}^{(i)}), y_{test}^{(i)})$$
- Model selection and training/validation/test sets

Training Set의 일부로 학습하여서, Training Error를 측정하면 실제 일반적인 Error보다 낮을 수가 있다.

만약 우리가 70% Training Set으로 가설함수의 최대 차수(degree) d를 1 ~ 10차의 가설함수를 구하고, Test Set으로 5-dimentions가 가장 적합하다고 선택을 했다. 하지만, 이렇게 선택한 Model도 Test Set에만 적합한 모델이 될 수 있으므로 적합한 평가가 될 수가 없고, Optimistic estimate of generalization error가 될 가능성이 있다. 따라서 단순히 Training/Test로 나누는 것이 아니라 적절한 d를 찾기 위한 Set이 필요하다.
따라서 우리는 다음과 같은 방법을 사용할 것이다.
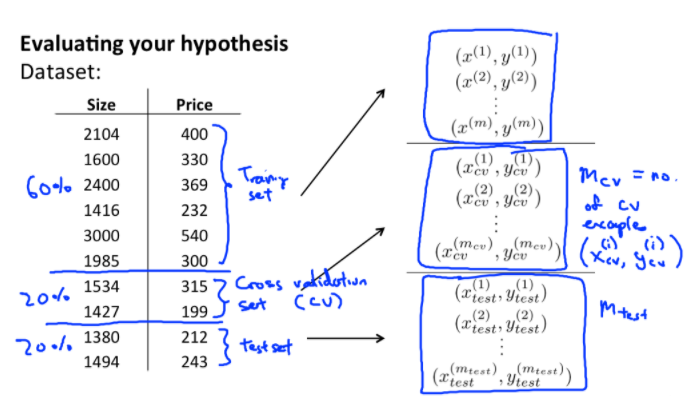
Training Examples을 위와 같이 Training Set, Cross Validation Set, Test Set 3가지 영역으로 분류한다. Training Set으로 여러가지 Model(d = 1, 2, 3, ...)에 대한 가설함수와 \(\theta\)를 구하고, Cross Validation Set을 통해 \(J_{CV}(\theta)\)를 구하여 최소가 되는 parameter d를 선택한다. 그리고 Test Error \(J_{test}(\theta)\)를 통해서 새로운 데이터와 오차를 확인하고, 가설함수가 적합한지 평가한다.
아래와 같은 공식으로 구하게 된다.

[Bias vs. Variance]
- Diagnosing Bias vs. Variance

학습 알고리즘을 학습할 때, 대부분 high bias(편차) 또는 high variance(분산)의 문제로 원하는대로 동작하지 않는다. High bias로 인해 underfitting(과소적합)이 발생하고, High variance로 인해 overfitting(과적합)이 발생한다.
보통 낮은 차수 d에서 underftting이 발생하며, 높은 차수 d에서 overfitting이 발생한다.
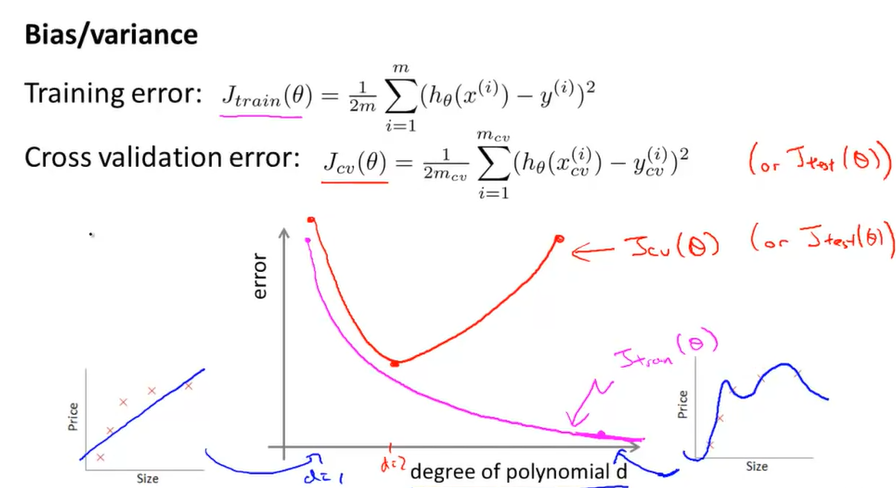
위의 그래프는 가설함수의 차수(degree of polynomial, d)와 그에 따른 Error를 나타낸다. 차수가 낮은 경우에는 Underfitting이 발생하고 Training Set과 CV Set에 대한 예측이 모두 적절하지 않다는 것을 보여준다(대체로 CV Set Error는 Test Set Error와 유사하다). 즉, \(J_{train}(\theta), J_{CV}(\theta)\)가 높게 나타난다. 반대로 차수가 높은 경우에는 Overfitting이 발생한다. 따라서, Training Set에는 너무 잘 맞기 때문에 \(J_{train}(\theta)\) 는 매우 낮지만, \(J_{CV}(\theta)\)는 높게 나타나는 것을 확인할 수 있다. 적절한 차수인 경우에는 \(J_{train}(\theta), J_{CV}(\theta)\)가 모두 낮게 나오는 것을 확인할 수 있다.
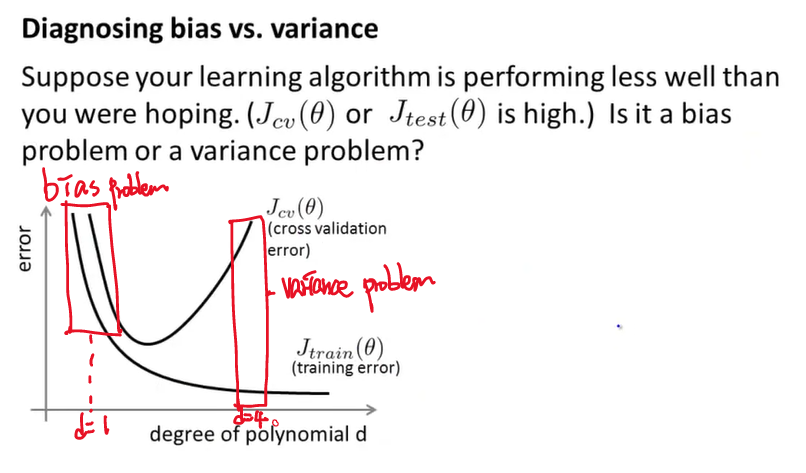
알고리즘의 성능이 기대에 미치지 못하는 경우에, 즉, \(J_{CV}(\theta)\) 또는 \(J_{test}(\theta)\)의 크기가 클 때, 이것이 bias 문제인지, variance 문제인지 어떻게 확인할 수 있을까?
위 그래프에서 볼 수 있듯이,
High Bias 문제는 \(J_{train}(\theta)\)와 \(J_{CV}(\theta)\)가 모두 크고, \(J_{CV}(\theta) \approx J_{train}(\theta)\) 이며,
High Variance 문제는 \(J_{train}(\theta)\)는 작고, \(J_{CV}(\theta) \gg J_{train}(\theta)\) 이다.
- Regularization and Bias/Variance
앞서 우리는 Overfitting 문제가 발생했을 때, Regularization(정규화)를 통해서 Overffiting 문제는 해결한다고 했었다.
아래와 같은 Linear regression with regularization의 예시 Model을 통해 살펴보자.
\(h_\theta(x) = \theta_0 + \theta_1x + \theta_2x^2 + \theta_3x^3 + \theta_4x^4\)
\(J(\theta) = \frac{1}{2m}\sum_{i = 1}^{m}(h_\theta(x^{(i)}) - y^{(i)})^2 + \frac{\lambda}{2m}\sum_{j = 1}{m}\theta_j^2\)
여기서 정규화 과정은 Cost Function \(J(\theta)\)의 두번째 항이며, 이것이 bias와 variance를 조절하게 된다.
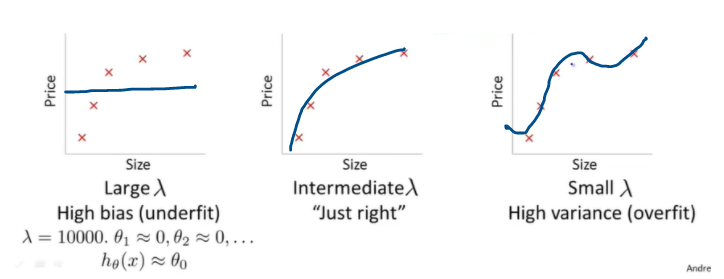
첫 번째 그래프는 \(\lambda\) 값이 너무 커서 underfitting을 발생시키고, 세 번째 그래프는 \(\lambda\) 값이 너무 작아서 regularization항이 영향을 거의 미치지 못해서 overfitting을 발생시킨다. 따라서, 가운데 그래프처럼 적절한 \(\lambda\)값을 선택하는 것이 중요하다.
어떻게 적절한 값을 선택할 수 있을까?
Choosing the regularization parameter \(\lambda\)
\(h_\theta(x) = \theta_0 + \theta_1x + \theta_2x^2 + \theta_3x^3 + \theta_4x^4\)
\(J(\theta) = \frac{1}{2m}\sum_{i = 1}^{m}(h_\theta(x^{(i)}) - y^{(i)})^2 + \frac{\lambda}{2m}\sum_{j = 1}{m}\theta_j^2\)
위와 같은 모델이 있을 때, 아래와 같은 방법으로 적절한 \(\lambda\)값을 구한다.
1. 0.01부터 2배씩 증가하여 10정도 까지의 \(\lambda\) 값을 가지고 각 \(\lambda\)값에 대해서 \(J(\theta\))를 최소로 만드는 \(\theta\)를 구한다.
2. 각 \(\lambda\)에 해당하는 \(\theta\)를 가지고 \(J_{CV}(\theta)\)를 구하고, 가장 작은 경우의 \(\lambda\)를 선택한다.
3. 선택한 모델을 가지고 \(J_{test}(\theta)\)를 구한다.

여기서는 5번째 \(\lambda\)값이 선택되었다.
Bias/Variance as a function of the regularization parameter \(\lambda\)
\(\lambda\)에 따른 \(J_{train}(\theta), J_{CV}(\theta)\)의 그래프는 다음과 같다.

\(\lambda\)가 클수록 underfitting 문제가 발생하므로, Training Set과 CV Set에 모두 잘 맞지 않으므로 \(J_{train}(\theta), J_{CV}(\theta)\)가 모두 크다.
그리고 \(\lambda\)가 작을수록 overfitting 문제가 발생하게 되고, Training Set과는 잘 맞으나, CV Set과는 잘 맞지 않으므로, \(J_{train}(\theta)\)는 작지만 \(J_{CV}(\theta)\)는 크다.
그래서 적절한 \(\lambda\)를 선택하는 것이 중요하다.
정리하면 다음과 같다.

[Learning Curves]
Learning Curve는 학습 알고리즘이 적절하게 동작하는지 확인하고, 알고리즘의 성능을 향상시키기 위해서 유용하게 사용되며, Bias 또는 Variance 등으로 문제가 발생하는지 진단해주는 도구이다.
Learning Curve는 Training Examples, m에 대한 \(J_{train}(\theta)\)와 \(J_{CV}(\theta)\)의 그래프를 그린다.
\(J_{train}(\theta) = \frac{1}{2m}\sum_{i = 1}^{{\color{blue}m}}(h_\theta(x^{(i)}) - y^{(i)})^2\)
\(J_{CV}(\theta) = \frac{1}{2m_{CV}}\sum_{i = 1}^{m_{CV}}(h_\theta(x_{CV}^{(i)} - y_{CV}^{(i)})^2\)
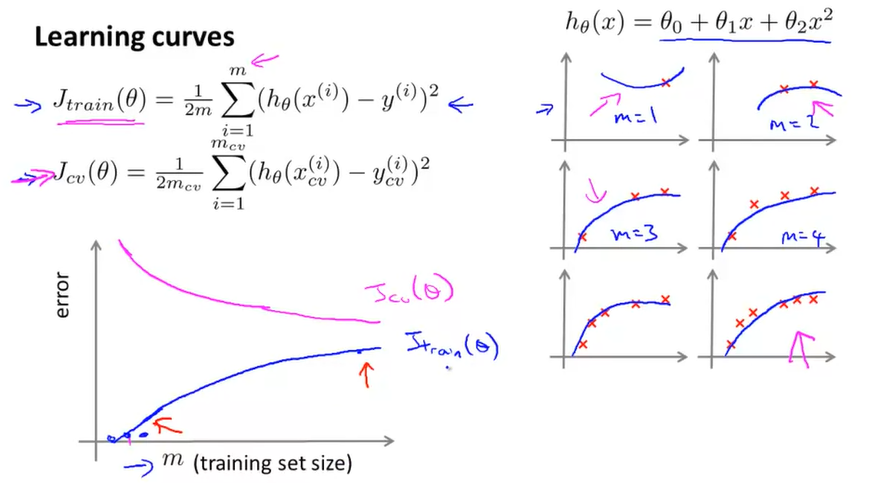
Learning Curve는 위와 같이 그려지게 된다.
m = 1, 2, 3인 경우에는 Training Set이 가설함수에 딱 맞기 때문에 Training Error는 0일 것이다. 하지만 Cross Validation Set에는 잘 맞지 않아서 CV Error는 높을 것이다. m = 4인 경우부터 Training Set이 완벽하게 가설함수에 들어맞지 않을 것이다. 따라서 m이 커질수록 가설함수에 딱 맞지 않아서 Training Error가 증가하며, 반대로 일반화된 모델에 가까워지므로 CV Error는 점점 감소하게 될 것이다.
Case 1: High Bias

High Bias에서 Training Set m이 작을 때, \(J_{train}(\theta)\)는 작을 것이고, \(J_{CV}(\theta)\)는 클 것이다.
반대로 m이 클 때는, \(J_{train}(\theta)\)와 \(J_{CV}(\theta)\)가 모두 클 것이다. \(J_{train}(\theta) \approx J_{CV}(\theta)\)
High Bias에서는 Training Error와 CV Error가 모두 크다. 그래서 High Bias 문제가 있으면, 단순히 더 많은 Training Data를 학습하는 것은 큰 도움이 되지 않는다.
Case 2: High Variance

High Variance에서 Training Set m이 작으면, High Bias와 마찬가지로 \(J_{train}(\theta)\)는 작을 것이고, \(J_{CV}(\theta)\)는 클 것이다.
반대로 m이 클 때는, \(J_{train}(\theta)\)는 증가하고, \(J_{CV}(\theta)\)는 leveling off(평준화)없이 감소할 것이다. 또한, \(J_{test}(\theta) < J_{CV}(\theta)\)이지만, \(J_{test}(\theta)\)와 \(J_{CV}(\theta)\)의 차이는 크다.
High Variance의 문제가 있다면, 더 많은 Training Data를 학습하는 것이 도움이 될 수 있다.
[Deciding what to try next (revisited)]
강의의 처음으로 돌아가서, 집값을 예측하는 regularized linear regression에서 새로운 input data에 대한 예측에 큰 에러가 발생한다면 어떤 방법을 시도해야할까?
- Training Example을 늘린다 -> fixes high variance
- Feature의 갯수를 줄인다 -> fixes high variance
- Feature의 갯수를 늘린다 -> fixes high bias
- Polynomial feature를 추가한다 -> fixes high bias
- \(\lambda\)를 감소시킨다 -> fixes high bias
- \(\lambda\)를 증가시킨다 -> fixed high variance
우리는 위와 같은 방법을 사용해서 High Bias or Variance의 문제를 해결할 수 있다.
- Neural networks and overfitting
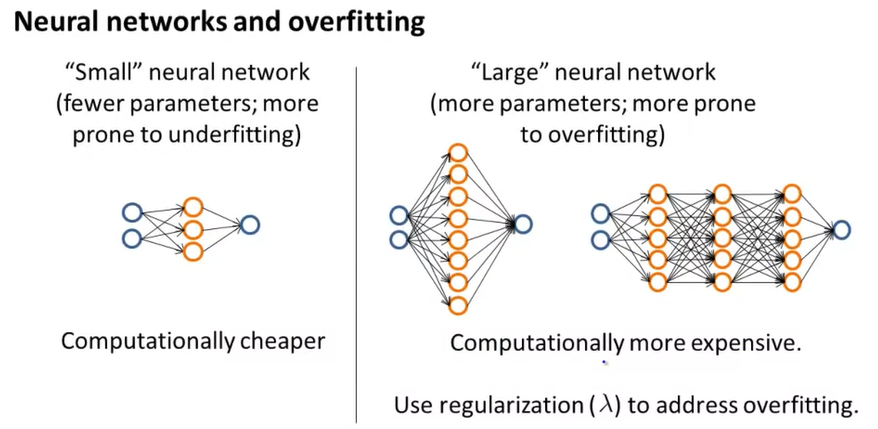
마지막으로 Neural Network에서의 underfitting과 overfitting을 살펴보자.
적은 수의 parameters는 계산 비용은 적고, underfitting 문제가 발생할 것이다(Small NN).
반대로 많은 parameters를 가진 NN은 계산 비용이 크고, overfitting 문제가 발생할 것이다. Overfitting이 발생하면 Regularization(정규화)를 사용해서 문제를 해결해야 한다.
하나의 Hidden Layer를 사용하는 것은 기본적으로 좋은 시작이 될 수 있다. 우리는 Hidden Layer의 수를 바꿔가며 CV Set을 사용해 NN을 학습할 수도 있고, 가장 좋은 성능을 가진 것을 선택하면 된다.
'Coursera 강의 > Machine Learning' 카테고리의 다른 글
| [Machine Learning] Machine Learning System Design (0) | 2020.08.20 |
|---|---|
| [Machine Learning] Exam 5 (Week 6) (0) | 2020.08.19 |
| [Machine Learning] Exam 4 (Week 5) (0) | 2020.08.18 |
| [Machine Learning] Backpropagation in Practice (0) | 2020.08.15 |
| [Machine Learning] Neural Network(Cost Function, Backpropagation Algorithm) (0) | 2020.08.15 |




댓글