해당 내용은 Andrew Ng 교수님의 Machine Learning 강의(Coursera)를 정리한 내용입니다.
이번 강의에서는 실제 예시들을 가지고 머신러닝을 구현할 때 고려해야될 사항들을 살펴보자.
- Building a Spam Classifier
[Prioritizing what to work on]
스팸메일인지 아닌지 구분하는 학습 알고리즘을 지도학습(Supervised Learning)으로 구현한다고 생각해보자.
\(x\) : features of email
\(y\) : Spam (1) or not Spam(0)
예를 들면, spam/not spam을 구분할 수 있는 100개의 단어(andrew, buy, deal 등)를 선택해서 feature \(x\)로 사용할 수 있다.
\(x = \begin{bmatrix} 0 \\ 1 \\ 1 \\ ... \\ ... \\ 1 \\ ... \end{bmatrix}, x \in \mathbb{R}^{100}, \text{ }x_{j} = \left\{\begin{matrix} 1 \text{ if word j oppears in email} \\ 0 \text{ if otherwise} \end{matrix}\right.\)
실제로는, 보통 Trainint Set에서 자주 나타나는 n개(10000 ~ 50000)의 단어를 선택한다.
우리는 아마 아래와 같은 방법으로 에러가 적도록 학습 알고리즘의 성능을 향상할 수 있을 것이다.
- Collect lots of data
- Develop sophisticated features based on email routing information (from email header)
- Develop sophisticated featrues for message body(또한, discount랑 discounts랑 같은 단어로 인식하는 알고리즘)
- Develop sophisticated algorithm to detect misspellings(e.g. m0rtagage, med1cine, w4tches.)
[Error Analysis]
추천하는 접근 방법은 다음과 같다.
- 빠르게 구현할 수 있는 간단한 알고리즘으로 시작을 한다. 그리고 Cross-Validation Data로 테스트한다.
- Learning Curve를 그려서 data가 더 필요한지, feature가 더 필요한지 등, 어떤 방법이 도움이 될지 결정한다.
- Error Analysis : CV Set에서 에러를 일으키는 Data들을 수동으로 분석한다. 어떤 유형의 Data가 Error를 발생하는지 찾아봐야한다.
예를 들어서 CV Set으로 500개의 예제가 있고, 알고리즘이 100개의 email을 잘못 분류하였다고 했을 때, 수동으로 100개의 Error를 분석하고, 아래와 같이 분류해야한다.
- What type of email it is
- Whate cues (features) you think would have helped the algorithm classify them correctly
계속 email 스팸 분류를 예시로 보자.
먼저 어떤 종류의 email이 Error를 발생하는지 확인해야한다. 여기서는 Pharmacy, Fake, Steal password 등의 종류가 있었고, 그 개수는 아래와 같다.

그리고, 어떤 것이 email 분류에 도움이 되는지 생각해야 한다. 예를 들면 철자를 일부러 틀리게 적는 것과, 잘못된 구두점 등을 feature로 추가하면 도움이 될 수도 있다.

여기서는 unusual punctuation의 경우가 많기 때문에, 이것을 검출하는 방법을 찾는 것이 효과적일 것이다.
[The importance of numerical evaluation]
여기서 discount / discounts / discounted / discounting을 같은 단어로 취급해야하는가 ? 이러한 문제는 'Stemming' 소프트웨어를 사용하면 해결이 가능하다(ex. 'Porter stemmer')
하지만 완벽하지 않다. 예를 들어서 universe를 university와 같은 단어로 취급하는 오류를 일으킬 수 있다.
Error analysis가 성능을 향상시키는데 도움이 안될 수도 있다. 결국 직접해보고 잘 동작하는지 확인해야 한다.
하지만, Stemming이 있건 없건 Numerical Evaluation(e.g., corrs validation error) 알고리즘은 중요하다.
실제로 적용하면 아래와 같이 성능 향상이 있다.

- Handling Skewed Data
[Error metrics for skewed classes]
다른 예로 Logistic Regression 강의에서 언급했던 암을 분류하는 예제를 생각해보자. Logistic Regression Model \(h_\theta(x)\)를 통해 \(y = 1\)이면 암, \(y = 0\)이면 암이 아니도록 예측하는 학습 알고리즘을 구현하였고, Test Set에서 1%의 에러만 있다고 하자. 수치상으로는 아무 문제없이 잘 동작하는 알고리즘으로 보이지만, 여기에는 큰 함정이 있다.
환자의 0.5% 만이 실제로 암이면 어떨까? 항상 \(y = 0\)으로 결정하는 알고리즘도 0.5%의 Error를 가질 수 있게 된다. 결국 1%의 Error가 딱히 좋은 성능이 아닐 수 있다. 이렇게 Data가 한 쪽으로 극단적으로 몰려있는 경우를 Skewed Class라고 한다.
Precision and Recall
Skewed Class로 인하여 생기는 문제를 방지하기 위해서 Precision/Recall 이라고 불리는 metric을 사용한다.
우리는 드물게 존재하는 class를 \(y = 1\)로 설정한다.
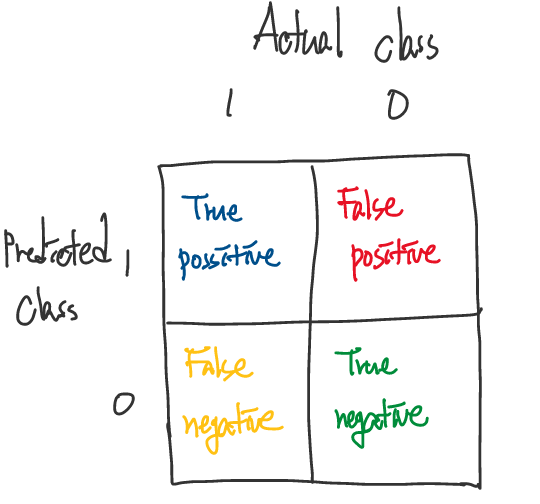
그리고, 우리가 예측한 결과 Class를 Predicted Class로, 실제 결과 Class를 Actual Class로 정의하고, Precision과 Recall을 정의하면 아래와 같다.
- Precision
Of all patients where we predicted \(y = 1\), what fraction actually has cancer?
우리가 y = 1이라고 예측하는 환자들 중에서 실제 암을 가진 환자의 비율
\(\frac{\text{True positive}}{\text{# predicted positive}} = \frac{\text{True positive}}{\text{True positive + False positive}}\)
- Recall
Of all patients that actually have cancer, what fraction did we correctly detect as having cancer?
실제 암이 걸린 환자들 중에서 우리가 정확하게 예측한 비율
\(\frac{\text{True positivie}}{\text{# actual positive}} = \frac{\text{True positive}}{\text{True positive + False negative}}\)
즉, Precision은 우리가 암이라고 예측한 환자들 중에서 실제 암에 걸린 환자의 비율을 나타낸 것이고, Recall은 실제 암에 걸린 환자들 중에서 우리가 학습 알고리즘으로 정확하게 예측한 비율을 의미한다.
[Trading off precision and recall]
Logistic Regression에서 결과는 아래처럼 예측이 가능하다.
Logistic Regreesion - \(0 \leq h_\theta(x) \leq 1\)
Predict 1 if \(h_\theta(x) \geq 0.5\)
Predict 0 if \(h_\theta(x) < 0.5\)

Logistic Regression을 이용하여 0과 1을 분류하고자 할 때, 우리는 Threshold(여기서는 0.5)를 정해서 분류를 한다.
하지만 우리가 매우 확실할 때만, y = 1이라고 결정하고 싶다면 Threshold 값을 0.5보다 더 높게 설정(0.7 or 0.9)하면 된다. 이렇게 되면 Higher Precision, Lower Recall을 갖게될 것이다.
반대로 우리가 많은 케이스의 암을 놓치는 것을 피하고 싶다면, Threshold를 더 낮게 설정(0.3)해서 암이라고 예측하는 경우를 높이면 된다. 이러면 Lower Precision, Higher Recall을 갖게될 것이다.
일반적으로는 \(h_\theta(x) \geq \text{ threshold}\)일 때, 1로 예측한다.
\(h_\theta(x)\)에 따라서 약간씩 다르지만, Precision과 Recall의 관계를 그래프로 표현하면 대체적으로 아래와 같이 표현된다.

우리는 어떻게 최적의 Threshold를 결정할 지 생각을 해봐야 한다.
[\(F_1\) Score(F Score)]
우리는 어떻게 Precision과 Recall을 비교할 수 있을까? 아래와 같은 3가지 경우의 알고리즘이 있다고 할때, 어떤 알고리즘이 성능이 가장 좋다고 판단할 수 있을까?

성능을 평가하기 위한 지표로 P와 R로 나타난다. 알고리즘을 평가하기에 한 가지의 지표로 판단하는 것이 훨씬 더 빠르고 도움이 되기 때문에 우리는 Single real number evaluation metric 방법을 사용할 것이다.
우리는 간단하게 두 지표의 평균으로 나타낼 수 있다.
Average : \(\frac{P + R}{2}\)
하지만 이 방법은 좋은 방법이 아니다. 3번째 알고리즘과 같이 항상 y를 1로 예측하는 알고리즘도 이 방법으로는 성능이 좋다고 판단(점수가 높다)될 수 있기 때문이다.
우리는 F-Score를 사용할 것이다.
\(F_1\) score = \(2\frac{PR}{P + R}\)

만약 \(P = 0\) 혹은 \(R = 0\) 이라면 F score는 0이 되고, 훌륭한 시스템은 \(P = 1, R = 1\)이기 때문에 F-score가 1이 된다.
F-score를 이용하면 알고리즘 1이 최적이 알고리즘으로 선택된다.
- Using Large Data Sets
[Data for machine learning]
이번 시간에는 얼마나 많은 데이터를 사용하는 것이 학습에 어떠한 영향을 끼치는지에 대해서 이야기를 할 것이다.
예를 들어서, 아래 빈칸에 적절한 단어를 넣어야 하는지를 학습시킨다고 하자.

이 학습 알고리즘을 학습하기 위해서 다양한 알고리즘을 사용하였고, 많은 Data를 사용하였다. 그리고 알고리즘에 따른 정확도는 아래와 같다.

위 그래프에서 볼 수 있듯이, 모든 알고리즘이 Training Data가 증가할수록 성능이 향상되는 것을 볼 수 있다.
또한, Training Set이 적을 때에 성능이 좋지 않았던 알고리즘이 Training Set이 많아질수록 다른 알고리즘보다 더 좋은 성능을 가질 수 있다는 것을 보여준다.
It's not who has the best algorithm that wins. It's who has the most data.
[Large data retionale]

우리가 만약 Feature x가 y를 정확하게 예측하기 위해서 충분한 정보를 가지고 있다고 가정할 때, 우리는 For breakfast I ate ___ eggs. 라는 예문에서 feature x는 주변 단어를 살펴보고 빈칸에 들어갈 단어를 정확하게 예측할 수 있을 것이다.
하지만, 집값을 예측하는 문제에서 다른 feature없이 size(\(feet^2\))만이 주어졌다면, 집값을 정확하게 예측하기는 어려울 것이다. 집값을 예측하기에는 집의 크기만으로는 정확한 예측을 할 수 없고 이런 경우에는 정보다 부족하다고 할 수 있다.
이것을 판단하는 유용한 방법은 input \(x\)가 주어졌을 때, 전문가가 확실히 \(y\)를 예측할 수 있는가는 확인해보는 것이다.

많은 Data를 사용하는 것은 도움이 될 것이다. 우리가 y를 예측하기에 충분한 정보를 가진 features가 있고, 많은 parameters를 가지고 학습 알고리즘을 사용한다고 가정해보자(maybe logistic regression or linear regression with a large number of features. Or neural network with many hidden units)
이것은 많은 parameters를 가진 강력한 학습 알고리즘이 되고, Low-Bias Algorithm이라고 생각할 수 있다.
따라서, Training Error \(J_{train}(\theta)\)는 작을 것이다. 또한 더 많은 Training Set을 활용한다면 Low-Variance Algorithm이 되어서 \(J_{train}(\theta) \approx J_{test}(\theta)\)이 되고, 많은 Feature를 사용하므로 \(J_{test}(\theta)\)도 \(J_{train}(\theta)\)를 따라서 줄어들 것이다.
'Coursera 강의 > Machine Learning' 카테고리의 다른 글
| [Machine Learning] SVM : Kernel (0) | 2020.08.23 |
|---|---|
| [Machine Learning] Support Vector Machine (2) | 2020.08.22 |
| [Machine Learning] Exam 5 (Week 6) (0) | 2020.08.19 |
| [Machine Learning] Advice for Applying Machine Learning 1 (0) | 2020.08.18 |
| [Machine Learning] Exam 4 (Week 5) (0) | 2020.08.18 |




댓글