해당 내용은 Andrew Ng 교수님의 Machine Learning 강의(Coursera)를 정리한 내용입니다.
[Unrolling Parameters]
NN에서 우리는 \(\Theta^{(l)}, D^{(l)}\)의 행렬 정의가 필요하다.
더 이상 \(\Theta\)는 vector가 아니고, octave 등에서 사용하기 위해서는 Unroll 과정이 필요하다.
\(s_1 = 10, s_2 = 10, s_3 = 1\)의 예시를 살펴보면, 아래와 같이 차원이 정의된다.
\(\rightarrow \Theta^{(1)} \in \mathbb{R}^{10 \times 11}, \Theta_{(2)} \in \mathbb{R}^{10 \times 11}, \Theta^{(3)} \in \mathbb{R}^{1 \times 11}\)
\(\rightarrow D^{(1)} \in \mathbb{R}^{10 \times 11}, D_{(2)} \in \mathbb{R}^{10 \times 11}, D^{(3)} \in \mathbb{R}^{1 \times 11}\)
Octave에서 'fminunc()' 함수에 사용할 수 있도록 위 행렬들을 최적화하는 것은 아래와 같다.
우선 하나의 긴 vector를 생성한다.
thetaVector = [ Theta1(:); Theta2(:); Theta3(:); ]
deltaVector = [ D1(:); D2(:); D3(:); ]Theta1의 차원은 10x11, Theta2는 10x11, Theta3는 1x11이고, 우리는 unroll된 벡터에서 해당 행렬을 얻을 수 있다.
Theta1 = reshape(thetaVector(1:110),10,11)
Theta2 = reshape(thetaVector(111:220),10,11)
Theta3 = reshape(thetaVector(221:231),1,11)요약하면, 아래와 같다. fminunc의 parameter인 @costFunction이 Cost(J)와 D를 구하는 함수이다.

[Gradient Checking]
BP를 진행하면서 문제가 없는지 확인하는 방법이며, 거의 모든 문제를 제거해준다. (항상 사용한다고 언급됨)
이 방법을 사용하면 높은 확률을 보장하고, FP나 BP가 100퍼센트 정확하도록 해준다.
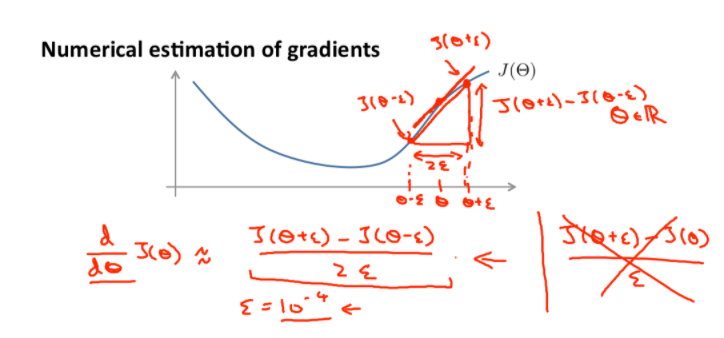
\(J(\Theta)\)의 그래프가 주어졌을 때, 어떤 값의 \(\Theta\)가 있다고 가정하자.
그리고 그 Theta값에서 \(\epsilon\) 만큼 떨어진 두 지점의 기울기를 이용하면 \(J(\Theta)\)의 미분계수를 추정할 수 있다. 미분의 정의가 \(\epsilon \rightarrow 0\)일 때의 변화량을 의미하므로, \(\epsilon\)이 매우 작다면 \(\Theta\)의 기울기와 비슷해질 것이다. 여기서 \(\epsilon\)의 값은 \(10^{-4}\) 정도이다.
Octave에서는 아래와 같이 실행된다.
gradApprox = (J(theta + EPSILON) - J(theta - EPSILON)) / (2*EPSILON)
Vector \(\theta\)에 적용하면 아래와 같다.

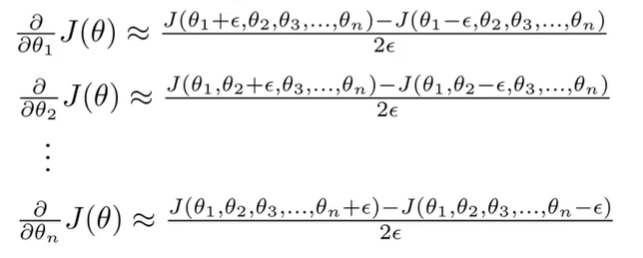
$$\frac{\partial}{\partial\Theta_j}J(\Theta) \approx \frac{J(\Theta_1, ..., \Theta_j + \epsilon, ..., \Theta_n) - J(\Theta_1, ..., \Theta_j - \epsilon, ..., \Theta_n)}{2\epsilon}$$
Octave에서는 다음과 같이 실행하면 된다.
EPSILON = 1e-4;
for i = 1:n,
thetaPlus = theta;
thetaPlus(i) = thetaPlus(i) + EPSILON;
thetaMinus = theta;
thetaMinus = thetaMinus(i) - EPSILON;
gradApprox(i) = (J(thetaPlus) - J(thetaMinus)) / (2*EPSILON);
end;그리고 Gradient Checking으로 계산된 gradApprox(i) 값과 BP로 계산된 미분계수 D가 같은지 확인하면 된다.
Check that gradApprox \(\approx\) DVec

정리하자면, BP로 미분계수 DVec를 구하고, Gradient Checking을 통해서 gradApprox를 계산한다. 그리고, 두 vector를 비교해서 유사한지 확인하고, Gradient Checking을 끄고, Training을 계속 진행한다.
여기서, 다시 Training을 하기 전에 Gradient Checking을 끄지 않으면 매 iteration마다 매우 큰 연산이 진행되어서 코드가 매우 느려질 수 있다.
[Random Initialization]
Gradient Descent나 Advanced Optimazation을 위해서는 우리는 \(\Theta\)를 초기화해주어야 한다.
만약 기존 방식처럼 모든 weight(즉, \(\Theta\))에 0으로 초기화를 하면 어떻게 될까?
결론은, Logistic Regression에서는 잘 동작하지만, NN에서는 정상적으로 동작하지 않는다.
- Zero initialization in Neural Network
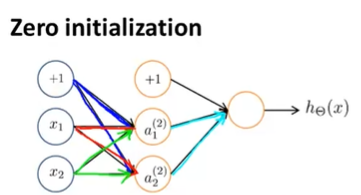
위와 같은 NN에서 우리가 모든 i, j, l에 대하여 \(\theta_{ij}^{(l)} = 0\)으로 초기화했다고 가정해보자.
그리고 FP를 진행하면, 다음과 같은 결과를 얻게 된다.
\(a_1^{(2)} = a_2^{(2)}\)
\(\delta_1^{(2)} = \delta_2^{(2)}\)
\(\frac{\partial}{\partial\theta_{01}^{(1)}}J(\theta) = \frac{\partial}{\partial\theta_{02}^{(1)}}J(\theta)\)
매 업데이트가 진행된 후에, 같은 layer에서 나온 parameter \(\theta\)는 같은 값을 가지게 된고, activation node의 값들도 같은 값을 가지게 된다.
0으로 초기화를 하면 위와 같은 문제가 생기기 때문에 우리는 다음과 같은 Random Initialization:Symmetry breaking을 사용해서 아래처럼 parameter를 초기화 한다.

즉, 모든 i, j, l에 대하여 parameter \(\Theta_{ij}^{(l)}\)은 \(-\epsilon\)이상 \(\epsilon\)이하의 값을 랜덤하게 갖고도록 초기화한다.
이때, \(\epsilon\)은 Gradient Checking과 무관하다.
Octave 코드로는 아래와 같이 실행된다.
% If the dimensions of Theta1 is 10x11, Theta2 is 10x11 and Theta3 is 1x11.
Theta1 = rand(10,11) * (2 * INIT_EPSILON) - INIT_EPSILON;
Theta2 = rand(10,11) * (2 * INIT_EPSILON) - INIT_EPSILON;
Theta3 = rand(1,11) * (2 * INIT_EPSILON) - INIT_EPSILON;0에서 2*INIT_EPSILON에서 랜덤값을 뽑아서, INIT_EPSILON을 빼서 -INIT_EPSILON에서 +INIT_EPSILON의 값을 갖도록 하는 것이다.
[Training a Neural Network]

NN을 학습시키기 위해서는 먼저 Network Architecture를 선택해야 한다. 즉, 뉴런들 을 어떠한 구조로 연결시킬 지에 대해서 결정해야 한다. 즉, Input과 Output의 unit 개수, Hidden Layer의 개수와 각 Hidden Layer unit의 개수를 결정해야 하고, 이에 따라 Network Architecture는 달라진다.
Input Unit : Feature \(x^{(i)}\)의 Dimension
Output Unit : Number of classes
그리고 Hidden Layer에 대해서 결정해야하는데, Hidden Layer 개수의 Default는 1이며, 1개 이상도 가능하다. 만약, Hidden Layer의 개수를 1개 이상으로 결정했다면, 각 Hidden Layer의 unit 갯수는 동일하도록 설정하는 것이 권장된다(보통 더 좋은 성능을 가진다).
또한, Hidden Unit의 개수는 많으면 많을 수록 좋다(must balance with cost of computation as it increases with more hidden units - 연산속도를 고려해야함)
Training a Neural Network는 다음과 같은 순서로 진행된다.
1. Randlmly initialize the weights
2. Implement forward propagation to get \(h_\Theta(x^{(i)})\) for any \(x^{(i)}\)
3. Implement the cost function \(J(\Theta)\)
4. Implement backpropagation to compute partial derivatives \(\frac{\partial}{\partial\Theta_{jk}^{l}}J(\Theta)\)
5. Use Gradient Checking to compare \(\frac{\partial}{\partial\Theta_{jk}^{(l)}}J(\Theta)\) computed using backpropagation vs. using numerical estimate of gradient of \(J(\Theta)\)
Then disable Gradient Checking code
6. Use Gradient Decent or advanced optimization method with backpropagation to try to minmize \(J(\Theta)\) as a function of parameters \(\Theta\)
우선 \(\Theta\)를 초기화 한다. 그리고 모든 Training Set(for i = 1 : m)에 대하여 학습을 해주면서 FP와 BP를 수행한다. 수행되면서 \(a^{(l)}, \delta^{(l)}, \Delta^{(l)}\)가 구해진다. 그리고 BP가 올바르게 동작하는지 Gradient Checking을 통하여서 확인해주고, 확인이 되면 해당 코드는 Disable한다. 그리고 Gradient Descent나 최적화된 방법을 통하여 최소의 \(J(\Theta)\)를 구해주면 된다.
NN의 경우에 Cost Function \(J(\Theta)\)가 non-convex해서 Local Optima로 수렴할 수도 있다. 하지만, 일반적으로는 큰 문제가 아니고, Global Optima을 찾는다고 보장할 수는 없지만 Gradient Descent나 다른 Optimization Method에서 매우 적합하게 잘 동작한다. 그래서 Cost Function \(J(\Theta)\)를 최소화하고, Global Optima에 도달하지 않더라도 아주 좋은 Local Optima을 얻을 수 있다.

위 그림은 2개의 Parameter를 갖는 NN에 대한 Gradient Descent 알고리즘의 수행을 보여주고 있다. 이 알고리즘은 Random 위치에서 시작해서 경사를 따라 내려가며 Optima를 찾는다. 최고점에서 \(h_\Theta(x^{(i)})\)는 실제값 \(y^{(i)}\)와 가장 큰 차이를 가지는 것이고, 최저점에서는 \(h_\Theta(x^{(i)})\)는 실제값 \(y^{(i)}\)에 가장 근접하다는 것이다. 여기서 BP는 Gradient Descent의 방향을 설정해주는 역할을 한다.
'Coursera 강의 > Machine Learning' 카테고리의 다른 글
| [Machine Learning] Advice for Applying Machine Learning 1 (0) | 2020.08.18 |
|---|---|
| [Machine Learning] Exam 4 (Week 5) (0) | 2020.08.18 |
| [Machine Learning] Neural Network(Cost Function, Backpropagation Algorithm) (0) | 2020.08.15 |
| [Machine Learning] Exam 3 (Week 4) (0) | 2020.08.14 |
| [Machine Learning] Neural Networks : Model Representation(신경망 모델) (0) | 2020.08.12 |




댓글