해당 내용은 Andrew Ng 교수님의 Machine Learning 강의(Coursera)를 정리한 내용입니다.
[Non-linear Hypotheses]
이때까지 우리는 linear regression과 logistic regression을 알아봤지만, 이 방법들은 복잡한 데이터를 처리하는데 한계가 있다. 예를 들어서 아래와 같은 데이터에서는 non-linear feature(요소)들을 가지고 logistic regression을 적용해야될 것이다.

기존에 배운 방식대로 Logistic Regression을 사용해서 non-linear boundary를 만들 수 있다. 그래프 오른쪽의 식처럼 고차원의 feature를 추가하면 된다.
가령, 이전에 살펴보았던 집값 예측 문제에서 집값을 결정하는 요소는 100개가 있다고 가정하고 이 집이 팔릴 것인가 판단하는 분류 문제로 변경하여서 살펴보자.

위와 같이 우리는 100개의 입력을 두 개씩 묶어서 새로운 feature로 사용한다고 하면, 5050개라는 feature가 생긴다. 실제 문제에서는 입력이 더욱 많은 경우가 많고, 이렇게 되면 feature의 개수가 너무 많이 증가해서 연산량이 늘어나서 느려지고, Overfitting(과적합)의 가능성이 높아진다.
다른 예로 Computer Vision을 살펴보자.
Car Detection을 위한 학습 알고리즘이 있고, 컴퓨터가 물체를 보고 이것이 차인지, 아닌지 판단한다.
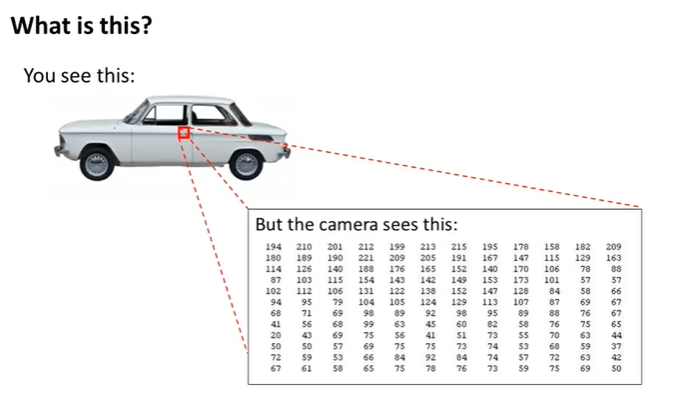
컴퓨터가 사진을 바라보는 방법을 알아보자. 빨간색 부분을 확대해서 보면, 컴퓨터는 해당 부분을 pixel(픽셀)들의 행렬로 본다. 그래서 이 알고리즘은 label training set을 가지고, 새로운 사진을 봤을 때 이 사진이 차인지 아닌지 판단하게 되는 알고리즘이다.
만약 아래와 같이 pixel1과 pixel2를 입력으로 예측하는 알고리즘이 있을 때, 해당 알고리즘을 Logistic Regression으로 표현하여, 그래프로 나타내면 아래와 같이 볼 수 있을 것이다.

그리고 만약 50 x 50 pixel images라면 입력으로 2500 pixels를 가지게 되며, 입력을 두개씩 묶어서 feature로 사용하게 되면 \( _{2500}C_2 = 3123750\) 로 매우 많은 feature를 갖게 되고, 계산이 오래걸리게 된다.
Neural Networks(신경망)
- Origin : Algorithms that try to mimic the brain
- Was very widely used in 80s and early 90s; popularity diminished in late 90s
- Recent resurgence: State-of-the-art technique for many applications
Neural network는 뇌를 모방하는 알고리즘으로, 뇌의 신경 세포를 모방하는 알고리즘을 개발하는 과정에서 등장했다. 80년대~90년대 초반에 많이 개발되다가, 90년대 후반에 인기가 감소했으나 최근 하드웨어의 발전으로 단순 계산에서 다양한 처리들이 가능해지면서, 현재는 다양한 분야에서 사용되는 최신의 기술이다.
The "one learning algorithms" hypothesis

동물 실험에서 귀와 Auditory Cortex 사이 연결을 끊고, 거기에 시신경을 연결하면 Auditory Cortex는 보는 법을 배운다고 한다. 즉, 이 증거는 뇌의 학습은 하나의 알고리즘을 이용해서 여러 가지의 감각을 학습할 수 있다는 가설을 뒷밤침한다.
[Model Representation]
어떻게 Neural Network를 표현하는지 알아보기 전에 실제 신경세포를 살펴보자.
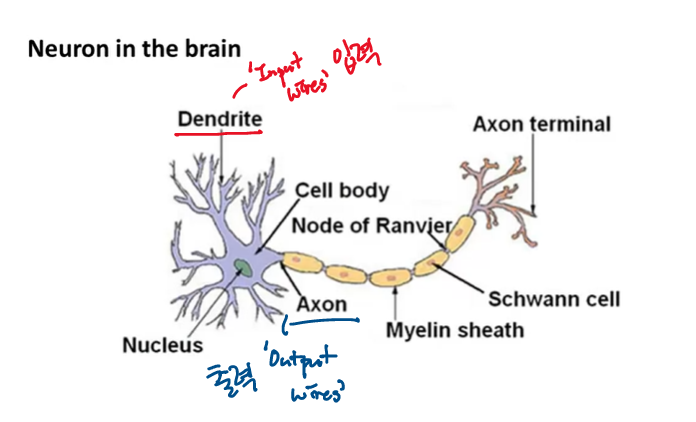
뉴런은 뇌의 세포이며, 뉴런은 Dendrite(수상돌기)에서 전기적 신호를 입력을 받아서 처리한 후에 Axon(축삭돌기)로 전달하는 세포이다.
Neuron Model : Logistic unit
뉴런은 아래와 같이 수학적 모델로 나타낼 수 있다. 신경망을 이용하여 가설함수(Hypothesis Function)을 나타낸 것이다.
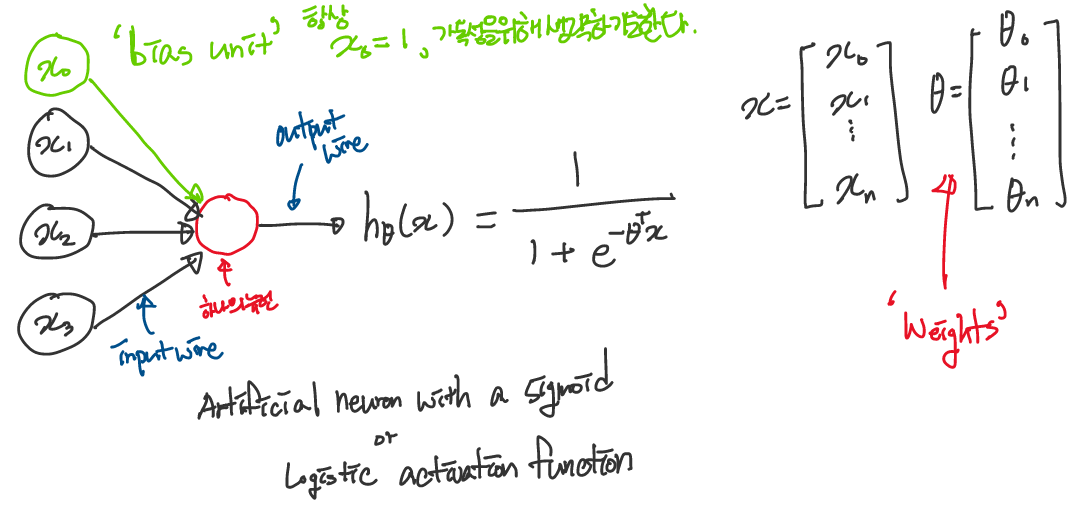
Dendrite의 input wires는 input feature \(x_1, x_2, ... x_n\) 으로 표현되고, Axon의 ouput wires는 Hypothesis Function의 ouput, 예측값으로 표현된다. 위에서 \(x_0\) 는 'bias unit'이라고 불리는데 항상 1의 값을 가지고, 편의상 생략하기도 한다.
Neuron Network에서는 Classification과 마찬가지로 sigmoid function \(\frac{1}{1 + e^{(-\theta^Tx)}}\) 를 사용하며, 위 모델 식은 Artificial neuron with a sigmoid 또는 Sigmoid(Logistic) activation function이라고 부른다.
여기서 \(\theta\) 는 Neuron Network 용어로 'Weights'(가중치)라고 하기도 한다.
위의 모델은 Single Neuron에 대한 모델이며, 실제 Artificial Neuron Network(인공신경망)을 살펴보자.
[Neural Network]

인공신경망은 이렇게 여러개의 뉴런들이 연결된 것이다.
여기서 Layer 1은 'Input Layer'로 feature들을 넣어주고, Layer 3은 'Output Layer'로 최종 계산된 값을 출력한다. Layer 2는 'Hidden Layer'라고 하며, 1개 이상의 Layer로 구성된다(Training Set에서 보이지 않기 때문에 Hidden이라는 이름을 가지고 있다).

이제 신경망에서 다이어그램이 의미하는 것이 무엇인지 살펴보자.
\(a_i^{(j)}\) 는 layer j에 있는 unit i의 'activation'(계산된 값이다)이며, \(\Theta^{(j)}\) 는 layer j에서 layer j+1로 매핑을 제어하는 가중치(weights) 행렬이다.
위 다이어그램은 아래와 같은 식으로 표현된다.
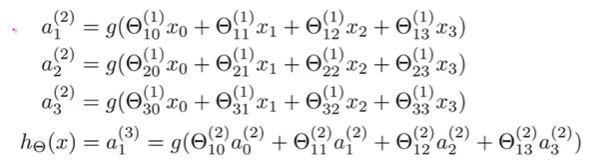
각각의 layer node는 위와 같이 계산한다.
여기서 layer 1에서 layer 2(activation node)의 계산은 3x4 matrix의 parameter \(\Theta^{(1)}\) 에 의해서 계산된 값에 sigmoid(logistic) function을 적용하여 구한다. layer 3(output layer)의 activation node 값은 앞에서 구한 layer 2와 1x4 matrix의 parameter \(\Theta^{(2)}\) 에 의해서 구해진 값에 sigmoid function(logistic function)을 적용해서 구한다. 즉, 마지막에 구한 \(a_1^{(3)}\) 이 \(h_\Theta(x)\) 가 된다.
이처럼 각 레이어는 고유한 weight matrix \(\Theta^{(j)}\) 를 갖는다. \(\Theta^{(j)}\) 의 크기는 layer j가 \(s_j\) 개의 unit을 갖고, layer j+1이 \(s_{j+1}\) 개의 unit을 갖는다면, \(\Theta^{(j)}\) 의 크기(dimention)는 \(s_{j+1} \times (s_j + 1)\) 이다. layer j의 '+1'은 'bias node' \(x_0 와 \Theta_0^{(j)}\) 로 인해 생긴다.
Output node에는 bias node을 포함하지 않지만, Input node에는 bias node을 포함한다.
인공신경망(Artificail Neural Network)는 Function \(h_\Theta(x)\) 를 정의하는 것인데, 이는 x를 입력받아 y를 예측하는 함수이다. 그리고 이 Hypothesis Function은 Parameter \(\Theta\) 에 의해서 조절되는데, 우리가 이 theta를 변화시킨다면, Hypothesis Function 또한 바뀔 것이다.
Forward propagation: Vectorized implementation
계속해서 아래의 신경망 예시를 살펴보자.
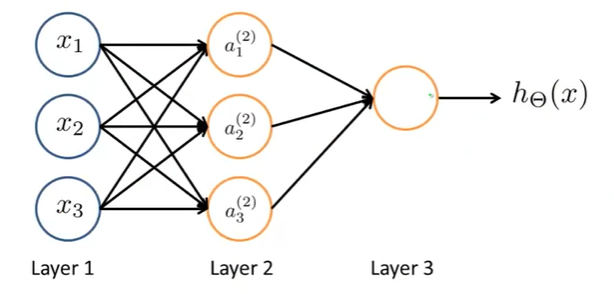
우리는 \(a_1^{(2)}, a_2^{(2)}, a_3^{(2)}\) 과 \(h_\Theta(x)\) 가 아래처럼 표현할 수 있다고 배웠다.
\(a_1^{(2)} = g(\Theta_{10}^{(1)}x_0 + \Theta_{11}^{(1)}x_1 + \Theta_{12}^{(1)}x_2 + \Theta_{13}^{(1)}x_3) = {\color{Red} g(z_1^{(2)})}\)
\(a_2^{(2)} = g(\Theta_{20}^{(1)}x_0 + \Theta_{21}^{(1)}x_1 + \Theta_{22}^{(1)}x_2 + \Theta_{23}^{(1)}x_3) = {\color{Red} g(z_2^{(2)})}\)
\(a_3^{(2)} = g(\Theta_{30}^{(1)}x_0 + \Theta_{31}^{(1)}x_1 + \Theta_{32}^{(1)}x_2 + \Theta_{33}^{(1)}x_3) = {\color{Red} g(z_3^{(2)})}\)
\(h_\Theta(x) = g(\Theta_{10}^{(2)}a_0^{(2)} + \Theta_{11}^{(2)}a_1^{(2)} + \Theta_{12}^{(2)}a_2^{(2)} + \Theta_{13}^{(2)}a_3^{(2)})\)
그리고 \(z\) 항으로 더 간단하게 표현할 수 있다.
이제 입력값들을 벡터로 일반화시켜 표현하여 더 간단하게 나타내면 아래와 같다.
\(x = \begin{bmatrix}x_0 \\ x_1 \\ ... \\ x_n \end{bmatrix}, z^{(j)} = \begin{bmatrix}z_1^{(j)} \\ z_2^{(j)} \\ ... \\ z_n^{(j)} \end{bmatrix}\)
이때, \(x = a^{(1)}\) 으로 치환하여 나타내면 더욱 간단히 나타낼 수 있다.
예제로 돌아와서 Layer 2에서 나오는 \(z^{(2)}\) 는
\(z^{(2)} = \begin{bmatrix}z_1^{(2)} \\ z_2^{(2)} \\ z_3^{(3)} \end{bmatrix} = \Theta^{(1)}x = \Theta^{(1)}a^{(1)}\) 이다.
그리고 \(a^{(2)} = g(z^{(2)}) \in R^3\) 이지만, bias unit \(a_0^{(2)} = 1\) 을 추가해서
\(a^{(2)} \in R^4\) 로 만들어서 나타내면 \(z^{(3)} = \Theta^{(2)}a^{(2)}\) 이다.
특히 Layer 1에서 x는 결국 \(a^{(1)}\) 을 뜻하기 때문에 일반화시켜 layer \(j\) 에 대해서 표현하면,
$$z^{(j)} = \Theta^{(j-1)}a^{(j-1)}$$
로 표현된다.
우리는 \(s_j \times (n + 1)\)(여기서 \(s_j\) 는 activation nodes의 수이다)의 차원을 가진 \(\Theta^{(j-1)}\) 행렬과 \((n + 1)\)의 높이(height)을 가진 \(a^{(j-1)}\) 벡터의 곱으로 \(s_j\)의 높이를 가진 벡터 \(z^{(j)}\) 를 구했다.
즉, \(a^{(j)} = g(z^{(j)})\)로 나타낼 수 있다.
결국 1 ~ \(j\) 의 layer가 존재한다고 했을 때,
Hypothesis Function \(h\) 는 아래와 같이 나타낼 수 있다.
$$h_\Theta(x) = a^{(j)} = g(z^{(j)})$$
최종 \(z\) vector는 \(\Theta^{(j-1)}\) 행렬과 activation node 행렬의 곱으로 구해지며, 최종 Theta matrix \(\Theta^{(j-1)}\)는 단 하나의 행을 가지므로(output layer의 activation node가 한 개이므로), \(z\)의 결과값은 single number가 된다.
※강의에서는 layer를 output을 제외해서 이야기하고 있다. 즉, layer j는 마지막 hidden layer를 의미하며, layer (j+1)은 ouput layer를 의미하고 있는 것 같다. 따라서 이와 같이 output layer가 (j+1)번째라고 한다면 아래와 같은 일반식을 얻을 수 있다.
$$h_\Theta(x) = a^{(j+1)} = g(z^{(j+1)})$$
이렇게 신경망 모델의 input layer부터 ouput layer까지 순서대로 이동하면서 가중치(Weight)를 곱해 계산하고 저장하는 것을 Forward Propagation(순전파)라고 한다.
Simple Example 1 : AND Gate
\(x_1\) AND \(x_2\) 를 예측하는 간단한 예제를 살펴보자.
입력은 \(x_1, x_2\)이며, 출력은 \(y = x_1\) AND \(x_2\)로 나타낼 수 있고, 신경망 모델로 나타내면 아래와 같다.

여기서 +1 은 bias unit(편향 특성)을 의미하고, \(\Theta^{(1)}\)을 아래와 같이 설정한다.
\(\Theta^{(1)} = \begin{bmatrix} -30 &20 &20 \end{bmatrix}\)
Hypothesis를 구하면 아래와 같고, \(x_1\)과 \(x_2\)가 모두 1일 때에만 1을 출력할 것이다.
\(h_\Theta(x) = g(-30 + 20x_1 + 20x_2)\)
| \(x_1\) | \(x_2\) | \(h_\Theta(x)\) |
| 0 | 0 | \(g(-30) \approx 0\) |
| 0 | 1 | \(g(-30) \approx 0\) |
| 1 | 0 | \(g(-30) \approx 0\) |
| 1 | 1 | \(g(-30) \approx 1\) |
이와 같이, 컴퓨터의 기본 연산 중 하나인 AND Gate를 작은 neural network를 사용하여 수행할 수 있다. Neural Network는 다른 논리 게이트를 수행할 수 있다.
OR Gate와 NOR Gate로 수행하기 위한 \(\Theta^{(1)}\)는 아래와 같다.
\(\text(NOR : \Theta^{(1)} = \begin{bmatrix}10 & -20 & -20 \end{bmatrix}\)
\(\text(OR : \Theta^{(1)} = \begin{bmatrix}-10 & 20 & 20 \end{bmatrix}\)
Simple Example 2 : XNOR Gate
우리는 Example 1의 논리 Gate를 조합하여서 'XNOR' 연산자를 만들 수 있다(\(x_1\)과 \(x_2\)가 모두 0이거나 1일 때만, 1을 출력하는 연산자).
\(\begin{bmatrix}x_0 \\ x_1 \\ x_2 \end{bmatrix} \rightarrow \begin{bmatrix} a_1^{(2)} \\ a_2^{(2)} \end{bmatrix} \rightarrow \begin{bmatrix} a^{(3)} \end{bmatrix} \rightarrow h_\Theta(x)\)
첫 번째 layer와 두 번째 layer의 변환을 위해서 우리는 \(\Theta^{(1)}\)를 아래와 같이 AND와 NOR의 조합을 사용한다.
\(\begin{bmatrix} -30 & 20 & 20 \\ 10 & -20 & -20 \end{bmatrix}\)
그리고 두 번째 layer와 마지막 layer(output layer)의 변환을 위해 \(\Theta^{(2)}\)를 다음과 같이 OR로 설정한다.
\(\begin{bmatrix} -10 & 20 & 20 \end{bmatrix}\)
각 activation node의 값과 Hypothesis을 표현하면 아래와 같다.
\(a^{(2)} = g(\Theta^{(1)}x)\)
\(a^{(3)} = g(\Theta^{(2)}a^{(2)})\)
\(h_\Theta(x) = a^{(3)}\)
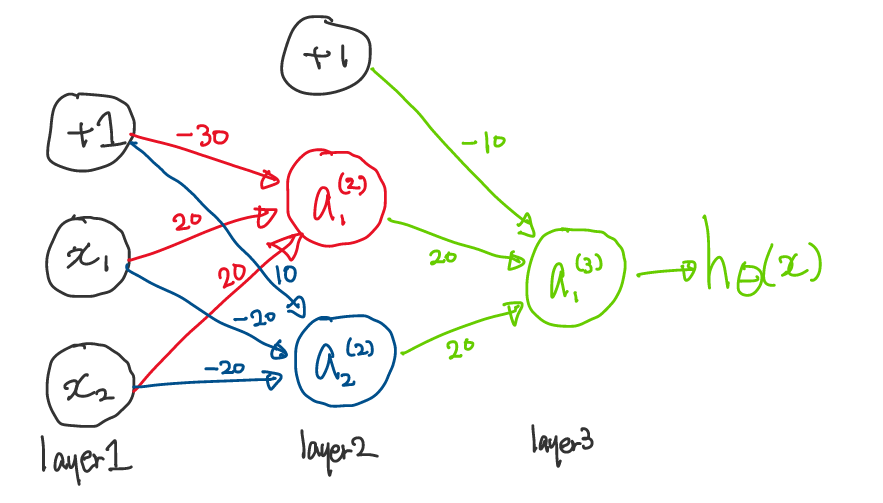
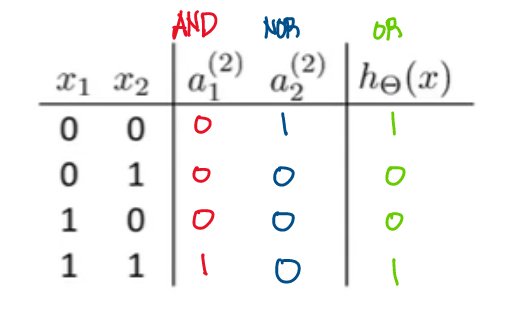
이렇게 다중 Neural Network로 XNOR 연산자를 수행하는 학습 알고리즘을 구현할 수 있다.
Multi-Class Classification
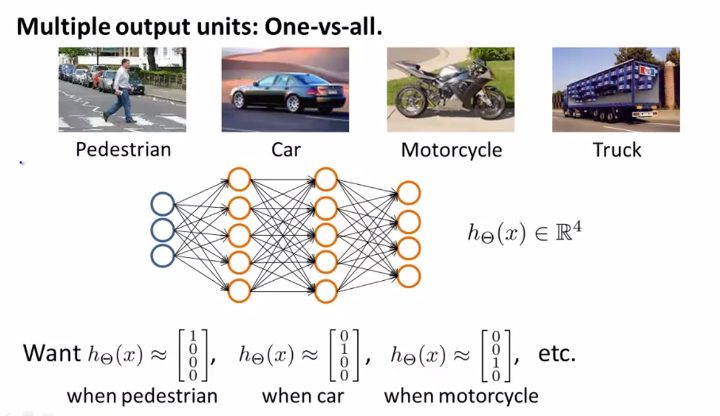
Neural Network를 사용해서 Multi-class classification 문제를 해결하기 위해서는 전에 언급했었던 One-vs-All 알고리즘을 사용해야 한다. 위에 사진의 Pedestrian, Car, Motorcycle, Truck를 구분하기 위한 예제를 살펴보자. 이렇게 4개의 카테고리로 분류하기 위해서는 4개의 Output Unit이 필요하며, 각각의 Unit의 값은 Binary Value를 갖는다. 결국, Output Layer는 4차원 Vector가 된다. 그리고 \(y^{(i)})\)는 가설함수 Hypothesis Function의 결과값(4차원 vector)가 될 것이고, 4개의 vector 중에 하나가 될 것이다.

'Coursera 강의 > Machine Learning' 카테고리의 다른 글
| [Machine Learning] Neural Network(Cost Function, Backpropagation Algorithm) (0) | 2020.08.15 |
|---|---|
| [Machine Learning] Exam 3 (Week 4) (0) | 2020.08.14 |
| [Machine Learning] Exam 2(Week 3) (3) | 2020.08.11 |
| [Machine Learning] Regularization 정규화 (0) | 2020.08.08 |
| [Machine Learning] Logistic Regression 2 (Cost Function, Gradient Descent, Multi-Class Classification) (5) | 2020.08.07 |




댓글