References
- 확률과 통계 강의 5, 6강 (KOWC - 한양대학교 이상화 교수님)
- Fundamentals of Applied Probability and Random Processs (Oliver Ibe)
Contents
- 평균, 기댓값 (Expectation)
- 분산 (Variance)
- 조건부 평균(Conditional Expectation)
기댓값 (Expectation)
산술 평균(arithmetic average)를 생각해봅시다. N개의 값 \(x_1, x_2, \cdots, x_N\)이 있을 때, 이 값들의 평균은 다음과 같이 계산됩니다.
\[\overline{X} = \frac{x_1 + x_2 + \cdots + x_N}{N}\]
이 때, 각각의 값들이 나타나는 빈도가 다르다면 각각의 값이 나오는 횟수를 \(w_1, w_2, \cdots, w_N\)으로 표현하여 다음과 같이 평균을 구할 수 있습니다.
\[\overline{X} = \frac{w_1 x_1 + w_2 x_2 + \cdots + w_N x_N}{w_1 + w_2 + \cdots + w_N}\]
여기서 \(w = n(S)\), 즉, Sample Space의 총 개수라고 생각할 수 있습니다. 그리고 각 \(w_i = n(A_i)\), 즉, 각 사건이 발생한 갯수로 생각할 수 있습니다. 이러한 정의를 통해, 확률 \(P(x_i)\)를 다음과 같이 계산할 수 있게 됩니다.
\[\frac{n(A_i)}{n(S)} = \frac{w_i}{\sum_{i=1}^{N}w_i} = P(x_i)\]
확률에서의 평균(mean)은 기댓값(Expectation, or expected value)이라는 용어를 사용하며, \(E[X]\)나 \(\overline{X}\)로 표기합니다. 확률의 기댓값은 다음과 같이 정의합니다.
\[E[X] = \overline{X} = \begin{cases} \sum_i x_i P(x_i) && \text{X discrete} \\ \int_{-\infty}^{\infty} x f_X(x)\mathrm{d}x && \text{X continuous} \end{cases}\]
개념이나 정의 자체는 어려운 부분이 없기 때문에 예제를 통해서 어떻게 구할 수 있는지 살펴보도록 하겠습니다.
Example 3.3
확률 변수 k에 대한 PMF가 다음과 같이 주어졌을 때의 기댓값을 구해보도록 하겠습니다.
\(\begin{matrix} p(k) = \frac{\lambda^k}{k!} e^{-\lambda} && k = 0, 1, 2, \cdots \end{matrix}\)
위 확률 분포에서 \(\lambda > 0\)이며, 이와 같이 주어지는 확률 분포를 포아송 분포(poisson distribution)이라고 부릅니다.
포아송 분포에서 평균을 계산하려면, 먼저 테일러 급수(tayler series)에 대해서 알고 있어야 합니다. 자세한 사항은 생략하고, 여기에서는 평균을 계산하기 위해 다음과 같은 식을 사용합니다.
\[e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \cdots = \sum_{k=1}^{\infty}\frac{x^k}{k!}\]
그럼 이제 확률 변수의 평균을 계산하는 정의를 통해 위의 PMF에 대한 기댓값을 계산해보겠습니다.
\[\begin{align*} E[K] = \sum_{k=0}^{\infty}k P_K(k) &= \sum_{k=0}^{\infty} k(\frac{\lambda^k}{k!}e^{-\lambda}) \\ &= \sum_{k=1}^{\infty} \frac{\lambda^k}{(k-1)!}e^{-\lambda} \\ &= \lambda e^{-\lambda} \sum_{k=1}^{\infty} \frac{\lambda^{k-1}}{(k-1)!} \\ &= \lambda e^{-\lambda} \sum_{m=0}^{\infty} \frac{\lambda^{m}}{m!} \\ &= \lambda e^{-\lambda} e^\lambda = \lambda \end{align*}\]
따라서, 포아송 분포의 기댓값 \(E[K]\)는 \(\lambda\)로 계산됩니다.
Example 3.4
이번에는 지수 분포(exponential distribution)의 기댓값을 계산해보겠습니다.
\[f_X(x) = \left \{ \begin{align*} & \lambda e^{-\lambda x} && x \geq 0 \\ & 0 && x < 0 \end{align*} \right.\]
마찬가지로 정의에 의해서 다음의 식을 통해 기댓값을 계산할 수 있습니다.
\[E[X] = \int_{-\infty}^{\infty} x f_X(x) \mathrm{d}x = \int_{0}^{\infty} x \lambda e^{-\lambda x} \mathrm{d}x\]
위의 식을 계산하면 \(E[X] = \frac{1}{\lambda}\)의 결과를 얻을 수 있습니다.
위의 두 예제를 통해서 두 확률 분포(포아송 분포, 지수 분포)의 기댓값이 상수값 \(\lambda\)에 의해서 결정되는 것을 확인할 수 있습니다.
분산 (Variance)
이번에는 분산을 살펴볼텐데, 그 전에 먼저 확률 변수의 모멘트(moment)에 대한 정의부터 살펴보겠습니다.
확률 변수 X의 n차(n-order) 모멘트는 다음과 같이 정의하며, \(E[X^n] = \overline{X^n}\)으로 표기합니다.
\[E[X^n] = \overline{X^n} = \left \{ \begin{align*} &\sum_i x_i^n P(x_i) && \text{X discrete} \\ &\int_{-\infty}^{\infty} x^n f_X(x) \mathrm{d}x && \text{X continuous} \end{align*} \right.\]
\(n = 1\)인 경우, 즉 1차 모멘트는 X의 기댓값 \(E[X] = \mu\)에 해당합니다.
또한, Central Moments(or moments about the mean)를 정의할 수 있습니다. 물리적인 의미로는 무게 중심에 해당합니다.
\[E[(X - \overline{X})^n] = \overline{(X-\overline{X})^n} = \left \{ \begin{align*} &\sum_i (x_i - \mu)^n P(x_i) && \text{X discrete} \\ &\sum_{-infty}^{\infty} (x - \mu)^n f_X(x) \mathrm{d}x && \text{X continuous} \end{align*} \right. \]
\(n = 1\)이라면,
\[\begin{align*} E[X - \mu] &= \int (x - \mu) f_X(x) \mathrm{d}x \\ &= \int x f_X(x) \mathrm{d} x - \mu \int f_X(x) \mathrm{d} x \\ &= \mu - \mu \cdot 1 = 0 \end{align*}\]
Central Moment의 값은 0이 됩니다.
\(n = 2\)일 때의 central moment는 매우 중요한데, 이때의 값을 분산(variance)라고 부릅니다. 일반적으로 \(\sigma_X^2\)로 표기하며, 다음과 같이 정의합니다.
\[\sigma_X^2 = E[(X-\overline{X})^2] = \left \{ \begin{align*} &\sum_i (x_i - \mu)^2 p_X(x_i) && \text{X discrete} \\ &\int_{-\infty}^{\infty} (x - \mu)^2 f_X(x) \mathrm{d} x && \text{X continuous} \end{align*} \right. \]
분산이 0이라면, 해당 확률 분포는 한 가지의 값이 100%로 나온다는 것을 의미합니다. 그리고 분산이 작으면 해당 확률 분포에서 data가 평균에 집중되어 있다는 것을 의미하며, 따라서, 예측이 쉽습니다. 반대로 분산이 크면 data가 넓게 고루 분포되어 있다는 것을 의미하며, 따라서 예측이 어려워집니다.
Proposition
확률 변수 X에 대해 두 함수 \(g_1(x), g_2(x)\)가 있고, \(g_3(x) = a g_1(x) + b g_2(x)\)로 정의했을 때, \(g_3(x)\)의 기댓값은 다음과 같이 계산할 수 있습니다.

이와 같은 성질을 만족하는 기댓값을 'Linear 하다', 또는 'Linearity를 만족한다'라고 말합니다. 선형대수나 신호 시스템과 같은 과목에서 이에 대한 정의가 주로 사용되는데, 자세한 내용은 생략하도록 하겠습니다.
위의 성질을 이용하여 분산을 다음과 같은 식으로 표현할 수 있습니다.
\[\begin{align*} \sigma_X^2 = E[(X - \mu)^2] &= E[X^2 -2X\mu + \mu^2] \\ &= E[X^2] -2\mu E[X] + \mu^2 \\ &= E[X^2] - \mu^2 \\ &= E[X^2] - (E[X])^2 \end{align*}\]
Example 3.7
연습문제 3.7은 위에서 살펴봤던 포아송 분포의 분산을 구하는 문제입니다.
이미 평균을 알고 있기 때문에 \(E[X^2] - \mu^2\)을 이용하여 분산을 구해보도록 하겠습니다.
분산을 구하기 위해 필요한 2차 모멘트 \(E[X^2]\)는 다음과 같이 계산할 수 있습니다.

테일러 급수에 의해서 아래의 계산 기법을 사용하면,

\(\sum_{k=1}^{\infty} \frac{k \lambda^{k-1}}{(k-1)!} = \frac{\mathrm{d}}{\mathrm{d}\lambda} \lambda e^\lambda = (1+\lambda)e^\lambda\)를 계산할 수 있습니다.
따라서, 포아송 분포의 2차 모멘트는 다음과 같이 계산됩니다.

결과적으로, 확률 변수 K의 분산은
\[\sigma_K^2 = E[K^2] - (E[K])^2 = \lambda + \lambda^2 - \lambda^2 = \lambda\]
로 계산됩니다.
포아송 분포의 평균과 분산은 모두 \(\lambda\)인 것을 확인할 수 있습니다.
Example 3.13
연습문제 3.13은 기하 분포(Geometric Distribution)에 관련된 문제입니다. 기하 분포에서 확률 변수 K는 성공할 때까지 시도한 횟수(# of trials until the first success)입니다. 예를 들면, 주사위를 반복적으로 던지는데 처음 6이 나올 확률에 대한 분포입니다. 일반적으로 성공할 확률을 p로 제공합니다.
\[P_K(k) = p(1 - p)^{k-1} \text{ , k = 1, 2, }\cdots \]
기하 분포에서 몇 가지 문제를 풀어보도록 하겠습니다.
(a) 먼저 기하 분포가 PMF를 만족하는지 확인해보도록 하겠습니다.
이는 Sample Space에서의 모든 확률의 합을 구했을 때 1을 만족하는지 확인해보면 됩니다.
\[\sum_{k = 1}^{\infty} p(1-p)^{k-1} = 1\]
확률 분포의 꼴이 무한 등비 급수에 해당하기 때문에 무한 등비 급수의 합을 구하는 공식을 사용하면 위 계산 결과가 1이라는 것을 쉽게 알 수 있습니다.
(b) 이번에는 \(P[K > 5]\)를 계산해보도록 하겠습니다.
\(K > 5\)인 확률은 K = 6부터 무한대까지 모두 더하면 됩니다. 따라서,
\[P[K>5] = \sum_{k=6}^\infty p(1-p)^{k-1} = p(1-p)^5 \sum_{k=6}^\infty (1-p)^{k-6}\]
여기서 또 무한 등비 급수의 합을 구하는 공식을 사용하게 되면, \(K > 5\)인 확률은
\[P[K>5] = (1-p)^5\]
가 됩니다.
(c) 이번에는 평균 \(E[K]\)를 구해보도록 하겠습니다.
정의에 의해서 평균은
\[E[K] = \sum_{k=1}^{\infty} kP_K(k) = \sum_{k=1}^{\infty} kp(1-p)^{k-1} = p \sum_{k=1}^{\infty} k(1-p)^{k-1}\]
로 계산할 수 있습니다.
이때,

\(\sum_{k=0}^{\infty} (1-p)^k\)를 \(G\)로 치환해서 계산하면,
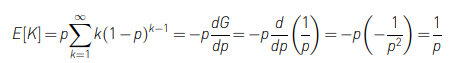
위와 같이 기하 분포의 평균을 구할 수 있습니다.
조건부 평균
조건부 평균(conditional expectation)은 평균이긴 하지만 제한이 추가된 평균입니다.
이산 확률 변수의 경우에는 다음과 같이 정의됩니다.
\[E[X|A] = \sum_{x_i \in A} x_i P_X(x_i | A) = \sum_{x_i \in A} x_i \frac{P(x_i \cap A)}{P(A)}\]
연속 확률 변수에서는 다음과 같이 정의됩니다.
\[E[X|A] = \int_{x \in A} x f_X(x | A)\mathrm{d}x\]
이때, \(f_X(x | A)\)는 조건부 PDF이며, 이를 바로 구해서 사용할 수 없기 때문에 우선 조건부 CDF를 통해서 조건부 PDF를 구해야 합니다.
\[\begin{align*} f_X(x | A) &= \frac{\mathrm{d}}{\mathrm{d}x} F_X(x | A) \\ &= \frac{\mathrm{d}}{\mathrm{d}x}P(X \leq x | A) \\ &= \frac{\mathrm{d}}{\mathrm{d}x} \frac{P(X \leq x \cap A)}{P(A)} \end{align*}\]
간단한 예제를 통해서 실제로 어떻게 조건부 평균을 구할 수 있는지 살펴보도록 하겠습니다.
Example 3.14
사건 A를 \(A = \{ X \leq a\} (-\infty < a < \infty)\)라고 가정할 때, \(E[X|A]\)를 구해보겠습니다.
먼저 조건부 PDF를 구해야 하는데, 이는 위에서 조건부 CDF를 통해 구하는 방식을 사용하여 구해야 합니다. 따라서, 다음의 식을 먼저 구합니다.
\[f_X(x | X \leq a) = \frac{\mathrm{d}}{\mathrm{d}x} \frac{P(X \leq x \cap X \leq a)}{P(X \leq a)} \]
x의 값의 크기에 따라서 분자에 해당하는 확률이 달라지기 때문에 두 구간 \(x \leq a\)와 \(x > a\)로 나누어서 생각해야 합니다.
먼저 \(x > a\)의 구간에 대해 살펴보면, \(P(X \leq x \cap X \leq a)\)는 \(P(X \leq a)\)가 됩니다. 따라서, 이 구간에서 \(f_X(x | X \leq A)\)는 0이 됩니다.
\(x \leq a\) 구간에서는 \(P(X \leq x \cap X \leq a)\)는 \(P(X \leq x)\)가 됩니다. 따라서,
\[f_X(x | X \leq a) = \frac{\mathrm{d}}{\mathrm{d}x} \frac{P(X \leq x)}{P(X \leq a)} = \frac{\mathrm{d}}{\mathrm{d}x} \frac{F_X(x)}{F_X(a)} = \frac{\frac{\mathrm{d}}{\mathrm{d}x}F_X(x)}{F_X(a)} = \frac{f_X(x)}{F_X(a)}\]
로 계산됩니다.
즉, 다음과 같습니다.
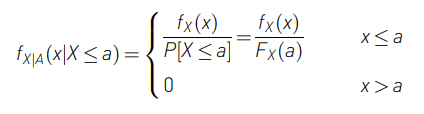
따라서, 조건부 평균 \(E[X|A]\)는 다음과 같이 계산됩니다.
\[E[X|A] = \frac{\int_{-\infty}^{a} x f_X(x) \mathrm{d}x}{F_X(a)}\]
'ML & DL > 확률과 통계' 카테고리의 다른 글
| 다중 확률 변수 (Multiple Random Variables) (0) | 2022.06.07 |
|---|---|
| 확률 분포 (Probability Distribution) (0) | 2022.05.30 |
| 확률 변수 (Random Variables) (0) | 2022.05.26 |
| 독립 사건과 순열 및 조합 (0) | 2022.05.24 |
| 조건부 확률과 베이즈 정리 (0) | 2022.05.22 |




댓글