확률 변수 (Random Variables)

References

• 확률과 통계 강의 3, 4강 (KOWC - 한양대학교 이상화 교수님)
• Fundamentals of Applied Probability and Random Processs (Oliver Ibe)

Contents

• (Discrete, Continuous) Random Variables(RVs) 
• Cumulative Distribution Functions (CDF)
• Probability Mass Function (PMF)
• Probability Density Function (PDF)

---

Definition of RV

Sample Space \(S\)의 무작위 실험을 가정해봅시다. 이때, \(w_1, w_2, \cdots\)는 \(S\)의 Sample Points라고 하겠습니다. 그리고 이러한 결과들 \(w_1, w_2, \cdots\)를 \(X(w)\)라는 함수를 통해 real number(실수)에 대응시켜주도록 하겠습니다. Sample Space의 하나의 결과는 반드시 하나의 실수와 대응되도록 만듭니다.

\[X(w) \rightarrow x\]

위의 매핑 함수에 의해서 \(w_1\)은 \(x_1\)에 매핑되고 \(X(w_1) = w_2\)는 \(X(w_2) = x_2\)에 매핑되도록 대응시킵니다. 이때, 대응되는 x에 해당하는 값들을 확률 변수(Random Variable)이라고 합니다.

 

 

정리하자면, 확률 변수(Random Variables; RVs)는 무작위 실험에서의 각 결과에 매핑(대응)되는 실수(real number)라고 정의할 수 있습니다.

 

예를 들어, 동전을 던지는 예제를 살펴보겠습니다.

동전은 실험을 수행할 때마다 앞면(H)과 뒷면(T)이 나올 수 있습니다. 그리고, 두 결과의 확률은 다음과 같습니다.

\[\begin{align*} P(H) = 1/2 \\ P(T) = 1/2 \end(align*)\]

이때, 이 실험에서의 각 결과 H와 T를 각각 1과 0에 대응시켜봅시다.

RV with coin tossing experiment

그렇다면 위의 두 확률은 다음과 같이 표현할 수 있습니다.

\[\begin{align*) P(H) = P(1) = 1/2 \\ P(T) = P(0) = 1/2 \end{align*}\]

대응되는 실수는 정의따라 얼마든지 변경될 수 있으며, T=1 / H=0으로 대응시켜도 상관없습니다.

간단히, 각 event에 대응되는 숫자를 확률 변수라고 할 수 있습니다. 이렇게 확률 변수를 사용하여 각 case에 대한 확률을 특정 숫자에 대한 확률로 대응시키게 되며, 이를 통해 확률을 하나의 함수로 다룰 수 있습니다.

 

 

이번에는 2개의 동전을 던지는 실험을 고려해봅시다. 이 실험에서 확률 변수는 앞면이 나오는 갯수로 정의합니다. 따라서, 각 사건을 다음과 같이 정의할 수 있습니다.

\[\begin{align*} \{TT\} \rightarrow 0 && P(0) = P(\{TT\}) = 1/4 \\ \{HT, TH\} \rightarrow 1 && P(1) = P(\{HT, TH\}) = 1/2 \\ \{HH\} \rightarrow 2 && P(2) = P(\{HH\}) = 1/2 \end{align*}\]

 

일반적으로 확률 변수는 대문자로 표기하며 각 확률 변수에서 하나의 값은 소문자로 표기합니다.

 

---

Event Defined by RV

이번에는 RV에 의해서 사건이 어떻게 정의되는지 살펴보겠습니다.

\(X\)를 확률 변수라고 하고, \(x\)를 확률 변수의 실수값이라고 하겠습니다. 이때, 사건 \(A_x\)를 Sample Space의 부분 집합으로 정의하는데, 이 사건은 실제 숫자 \(x\)를 할당하는 확률 변수 \(X\)의 실제 Sample Points로 구성되어 있는 집합입니다. 즉, 다음과 같이 \(A_x\)를 정의할 수 있습니다.

\[A_x = \{w | X(w) = x\}\]

 

2개의 동전을 던지는 예제를 이에 적용하면 \(A_0 = \{TT\}, A_1 = \{HT, TH\}\)가 됩니다.

\(A_x\)가 사건이기 때문에, 이들은 확률을 가지며 해당 사건의 확률은 다음과 같이 표현합니다.

\[P(A_x) = p\]

마찬가지로 2개의 동전을 던지는 예시에서 \(P(A_1)\)는 이제 다음과 같이 표현할 수 있습니다.

\[P(A_1) = P(1) = 1/2\]

 

일반적으로 확률 변수 X에 대한 사건 집합의 확률은 다음과 같이 표현합니다.

\[P(A_x) = P_x (X = x)\]

 

그리고 A라는 사건이 \(a < X \leq b\)일 때, 확률 변수를 이용하여 다음과 같은 타입의 사건을 정의할 수도 있습니다. 

\[P(A) = P(a < X \leq b) = P(\{w|a < X(w) \leq b\})\]

 

다시 2개의 동전을 던지는 실험을 예로 들어, \(P(X \leq 1)\)은 \(x = 0, x = 1\)일 때의 확률을 구하라는 것이기 때문에 다음과 같이 작성할 수 있습니다.

\[\begin{align*} P(X \leq 1) &= P(\{TT, HT, TH\}) \\ &= \frac{3}{4} \\ &= F_X(1) \end{align*}\]

이때, \(P(X \leq 1)\)과 같은 형태의 확률 값을 Cumulative Distribution Function(CDF)로 나타내어 \(F_X(1)\)로 표현할 수 있습니다.

 

---

Cumulative Distribution Functions

위에서 \(P(X \leq 1\)\)과 같은 형태의 사건을 정의했습니다. 이를 \(F_X(1)\)로 표현할 수 있다고 언급했는데, 이렇게 표현되는 함수를 누적 분포 함수(Cumulative Distribution Functions; CDF)라고 하며, 다음과 같이 정의합니다.

\[\begin{matrix}F_X(x) = P(X \leq x) & -\infty \leq x \leq \infty \end{matrix}\]

아마, 고등학교 때 배운 누적 도수 분포표가 이와 유사합니다. 

 

누적 분포 함수

누적 분포 함수는 다음과 같은 성질들을 가지고 있습니다.

1. 만약 \(x_1 < x_2\)라면, \(F_X(x_1) \leq F_X(x_2)\)를 만족합니다. 즉, CDF는 non-decreasing function입니다. 여기서 등호(equality)는 \(P(x_1 < X \leq x_2) = 0\)일 때 성립합니다.
2. \(0 \leq F_X(x) \leq 1\).
3. \(F_X(\infty) = \lim_{x \rightarrow \infty} F_X(x) = 1\)
4. \(F_X(-\infty) = \lim_{x \rightarrow -\infty} F_X(x) = 0\)
5. \(P(a < X \leq b) = F_X(b) - F_X(a)\)
6. \(P(X > a) = 1 - P(X \leq a) = 1 - F_X(a)\)

위 성질에서 나오는 등호(equality)는 확률 변수가 discrete(이산)인 경우에는 주의깊게 살펴봐야 합니다. 연속(continuous) 확률 변수인 경우에는 등호가 크게 영향을 미치지 않습니다.

 

간단한 예제 문제(Example 2.3)를 살펴보도록 하겠습니다.

확률 변수 X의 CDF가 다음과 같이 주어진 경우,

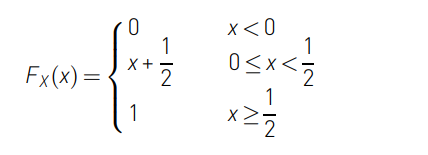
CDF를 그래프로 표현하면 다음과 같습니다.

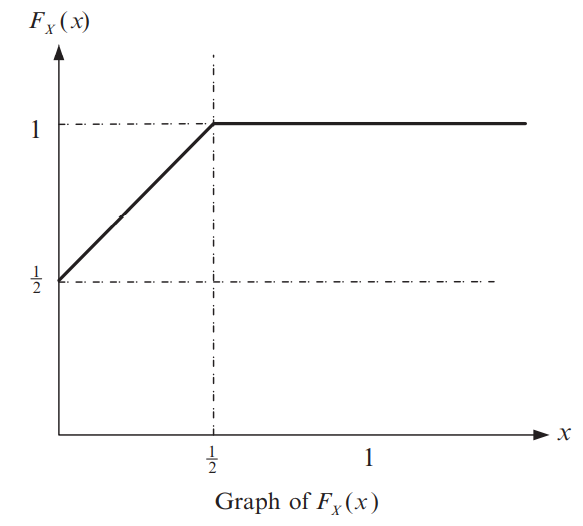
그리고 위 CDF에서 \(X\)가 1/4보다 큰 확률을 구하면,

\[P(X > \frac{1}{4}) = 1 - P(X \leq \frac{1}{4}) = 1 - F_X(\frac{1}{4}) = 1 - (\frac{1}{4} + \frac{1}{2}) = \frac{1}{4}\]

가 됩니다.

 

---

Discrete Random Variables

이산 확률 변수(Discrete Random Variables)는 연속적이지 않은(non-continuous) 확률 변수를 의미합니다. 주로 정수값을 다루게 되며, 경우의 수 하나하나를 카운트할 수 있는(countable) 확률 변수입니다.

 

이산 확률 변수에서는 확률 질량 함수(Probability Mass Function, PMF)를 정의할 수 있습니다. 따라서, 다음과 같이 확률 변수 x에 대한 확률을 구할 수 있습니다.

\[P_X(x) = \text{Prob}(X = x)\]

즉, \(P_X(X = x_i)\)를 특정할 수 있으며, 이때 \(x_i\)는 유한할 수도 있고 무한할 수도 있습니다(무한하다고 해서 셀 수 없는 것은 아닙니다).

이때, 이산 확률 변수의 CDF는 다음과 같이 계산될 수 있습니다.

\[\begin{align*} F_X(x) &= P(X \leq x) \\ &= \sum_{i \leq x} P_X(x_i) \end{align*}\]

 

다시 한번, 위에서 언급했던 2개의 동전을 던지는 예제를 살펴봅시다. 이때, 확률 변수를 동전을 던져서 나오는 앞면의 갯수라고 정의했습니다. 따라서, 확률 변수는 0, 1, 2라는 정수값이 되는데, 이것이 바로 이산 확률 변수입니다.

이 확률 변수의 PMF는 다음과 같이 정의할 수 있습니다.

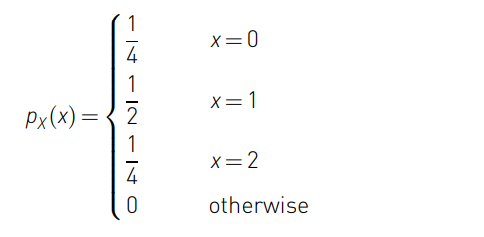
그리고, CDF는 다음과 같이 정의됩니다.

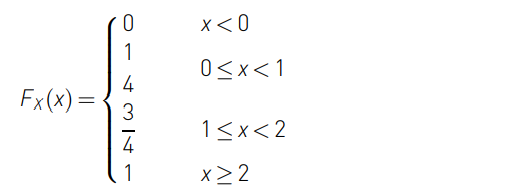
두 함수의 그래프를 그리면, 다음과 같습니다. 

 

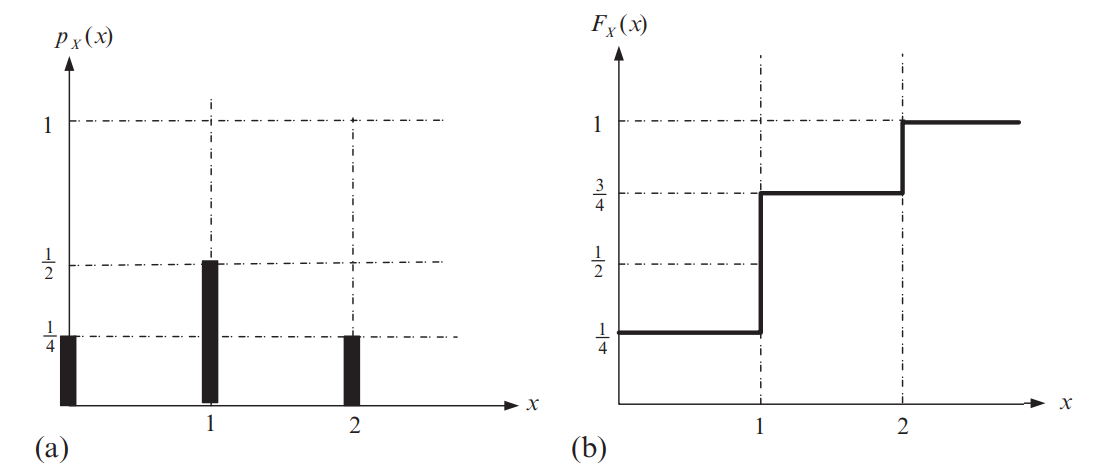
PMF에서 각 확률 변수의 막대(확률)을 델타 함수, \(\delta(x)\)로 표현할 수 있습니다. 여기서 델타 함수는 다음과 같이 정의됩니다.

\[\delta(x) = \left\{\begin{matrix} 0 && x \neq 0 \\ 1 && x = 0 \end{matrix}\right.\]

델타 함수를 사용하면 PMF를 함수처럼 사용할 수 있습니다. 위의 동전 던지기 예시에서의 PMF를 함수로 표현하면 다음과 같이 표현할 수 있습니다.

\[P_X(x) = \frac{1}{4}\delta(x) + \frac{1}{2}\delta(x-1) + \frac{1}{4}\delta(x-2)\]

위 PMF 함수를 일반화하면, 다음과 같이 표현할 수 있습니다.

\[P_X(x_i) = \sum_{i}P(X=x_i)\delta(x-x_i)\]

 

---

Continuous Random Variables

연속 확률 변수(Continuous Random Variables)는 가능한 결과(경우)들을 셀 수 없는(uncountable) 모든 real number(실수) 공간에 매핑합니다. 즉, Sample Space \(S\)를 실수 공간 \(\mathbb{R}\)에 매핑하는데, 이때 매핑되는 공간에서 구간은 (a, b)처럼 제한될 수도 있고, (\(-\infty, \infty\))와 같이 무한할 수도 있습니다.

 

간단하게 (0, 1) 구간에서 정밀도(precision)을 무한대로 설정하고 하나의 숫자(ex, 0.500000...)을 뽑는다고 가정해봅시다. 모든 숫자들이 뽑힐 확률은 동일하다고 볼 수 있고, 정밀도가 무한하기 때문에 (0, 1) 사이에 존재하는 숫자의 개수는 셀 수 없습니다. 따라서, 하나의 숫자, 예를 들어, 0.50000... 을 뽑을 확률은 다음과 같습니다.

\[P(0.5000\cdots) = \frac{1}{\infty} = 0\]

엄밀히 말하자면, 하나의 숫자를 뽑을 확률이 정확히 0은 아닙니다. 하지만, 이를 극한 개념으로 확장하여 0이라고 말합니다.

 

연속 확률 변수는 셀 수 없기 때문에, 하나의 특정한 경우의 확률을 구하는 것이 불가능합니다. 따라서, 이산 확률 변수처럼 \(P(X = x_i)\)처럼 하나의 경우에 대해 인덱싱하는 것이 불가능하며, 일반적으로 극한의 개념을 사용하여 하나의 경우에 대한 확률은 0이라고 말합니다.

 

연속 확률 변수에서는 각각의 확률 변수에 대해 확률을 정의하는 것이 불가능하기 때문에 PMF를 정의할 수 없습니다.

 

그렇다면 특정 작은 구간에 대한 확률 \(P(x < X \leq x + \Delta x)\)을 고려해보겠습니다. 그리고 이 구간에 대해 0으로 수렴(\(\lim_{\Delta x \rightarrow 0}\))하도록 해봅시다.

\[\lim_{\Delta x \rightarrow 0} P(x < X \leq x + \Delta x) = \lim_{\Delta x \rightarrow 0} F_X(x+\Delta x) - F_X(x) \rightarrow 0\]

특정 작은 구간에 대한 확률을 CDF 정의를 이용해서 표현할 수 있습니다. 그리고, \(\Delta x\)가 0으로 수렴하기 때문에 위 식의 값은 결과적으로 0으로 수렴하게 된다는 것을 알 수 있습니다. 구간에 대한 확률이 0은 아니기 때문에, 이를 만족시키기 위해서 위 식을 \(\Delta x\)로 나누어 보겠습니다. 그렇게 되면 위 식을 CDF의 미분으로 표현할 수 있게 되고 이를 \(f_X(x)\)로 표현하도록 하겠습니다.

\[f_X(x) = \lim_{\Delta x \rightarrow 0} \frac{F_X(x + \Delta x) - F_X(x)}{\Delta x} = F_X'(x)\]

이때, \(f_X(x)\)를 확률 밀도 함수(Probability Density Function, PDF)라고 합니다. 이를 이용하여 연속 확률 변수의 확률 분포를 정의할 수 있습니다.

 

물리적인 의미로 살펴보면, 확률을 길이 \(\Delta x\)로 나눈 것인데, 즉, 단위 길이 당 확률로 표현한 것입니다. 이 때문에 밀도라는 단어가 포함됩니다. 예를 들어, 어느 한 공간에 산소 분자가 얼마나 있는가에 대한 질문을 생각해보면 도움이 될 것 입니다. 그때그때 마다 어느 공간에 존재하는 기체 분자의 개수는 다를 것이고, 따라서 세기 힘들다는 것을 쉽게 알 수 있습니다. 이때, 우리는 주로 밀도라는 개념을 사용하여 어느 정도 존재할 것이다라고 추측합니다. 즉, 확률의 개념이 포함되는 것을 확인할 수 있습니다.

 

PDF의 특징은 다음과 같은데, PMF와 유사합니다. 그 중 \(f_X(x)\)가 PDF이기 위해서는 1, 2번 성질을 동시에 만족해야 합니다.

1. \(f_X(x) \geq 0\), 즉, PDF는 non-negative 함수입니다.
2. \(\int_{-\infty}^{\infty} f_X(x)\mathrm{d}x = 1\): 이는 \(F_x(\infty)\)와 같습니다.
3. \(P(a < X \leq b) = F_X(b) - F_X(a) = \int_{-\infty}^{b}f_X(x)\mathrm{d}x - \int_{-\infty}^{a}f_X(x)\mathrm{d}x = \int_{a}^{b} f_X(x)\mathrm{d}x\). 이 정의에 의해서 특정한 값의 확률 \(P(X = a) = \int_{a}^{a}f_X(x)\mathrm{d}x = 0\)이 됩니다.
4. \(P(X < a) = P(X \leq a) = \int_{-\infty}^{a} f_X(x)\mathrm{d}x = F_X(a)\)

4번 성질에서 알 수 있듯이, 연속 확률 변수에서의 등호(equality)는 크게 중요하지 않습니다.