References
- Programming Massively Parallel Processors
Contents
- Sparse Matrix, CSR
- Parallel SpMV Using CSR
- ELL Format
- Hybrid Approach to Regulate Padding
본문에 사용된 코드는 아래 링크에서 확인하실 수 있습니다.
GitHub - junstar92/parallel_programming_study: Study parallel programming - CUDA, OpenMP, MPI, Pthread
Study parallel programming - CUDA, OpenMP, MPI, Pthread - GitHub - junstar92/parallel_programming_study: Study parallel programming - CUDA, OpenMP, MPI, Pthread
github.com
Background
Sparse Matrix(희소 행렬)이란 행렬의 값이 대부분 0인 행렬을 의미합니다. 희소 행렬은 많은 과학, 공학, 회계 모델링 문제에서 발생합니다. 또한, 행렬은 선형 시스템에서 계수를 표현하는데 사용될 수 있는데, 행렬의 각 행은 선형 시스템의 방정식 하나를 나타냅니다.

위 행렬이 방정식을 표현하는데 사용되면, 행렬의 각 열은 변수의 계수가 될 수 있고, 각 행은 방정식(equation)을 의미합니다. \(x_0\)은 column 0, \(x_1\)은 column 1이 됩니다. 예를 들어, row 0에서 column 0과 2에 0이 아닌 원소가 있다는 것은 row 0의 방정식이 변수 \(x_0\)과 \(x_2\)가 연관되어 있음을 알 수 있습니다.
희소 행렬은 일반적으로 값이 0인 요소들의 저장을 피하는 형식으로 저장되고 표현됩니다. 아래 이미지에 나와있는데 Compressed Sparse Row (CSR) 저장 포맷을 살펴보겠습니다.

CSR은 위 이미지에서 data[]로 표시된 것처럼 0이 아닌 값만 1차원 데이터에 저장합니다. data[] 배열은 Fig.1의 희소 행렬의 0이 아닌 값만 1차원 데이터에 저장하고 있습니다. Row 0의 0이 아닌 요소 3과 1, Row 2의 요소 2, 4, 1, Row 3의 요소 1, 1이 저장되어 있습니다. 이 포맷은 값이 0인 요소들을 압축하여 data[] 배열에 저장하지 않도록 합니다.
이렇게 압축된 포맷을 사용하면, 압축된 포맷에서 원래 희소 행렬의 구조를 보존하기 위해 두 세트의 마커를 입력하는데, 이것이 바로 Fig.2의 Column indices와 Row Pointers 입니다.
Column indices는 Fig.1의 column 인덱스 배열인 col_index[]를 형성합니다. 이 배열은 원래의 희소 행렬에서 0이 아닌 모든 값의 column 인덱스의 값을 저장하고 있습니다. 이 마커를 사용해서 희소 행렬에서 저장된 값들의 원래 위치를 기억합니다. 예를 들어, Row 0의 3과 1의 열 인덱스인 0과 2가 col_index[0], col_index[1]에 저장됩니다.
두 번째 마커인 Row Pointers는 0이 제거된 후에 각 행의 크기가 달라지기 때문에 압축된 포맷에서 모든 행의 시작 위치를 나타냅니다. 압축된 data에 있는 각 행의 시작 위치는 더 이상 고정 행 크기에 기반한 인덱싱을 사용하여 식별할 수 없습니다. row_ptr[] 배열을 보면, row_ptr[0]은 data[] 배열에서 Row 0의 시작 지점인 0을 나타내고, row_ptr[1]은 Row 1이 시작되는 위치 2를 나타냅니다. Row 1의 요소는 모두 0이기 때문에 저장된 요소가 없고, 따라서 Row 2의 시작 위치인 row_ptr[2]에 다시 2가 저장됩니다. 여기서 row_ptr[4]는 Fig.1의 희소행렬에서 존재하지 않는 Row 4의 시작 위치를 저장하고 있는데 이는 옵션입니다. 이를 사용하면 Row 3의 끝 위치를 쉽게 찾을 수 있습니다.
처음에 이야기했듯이 행렬은 방정식을 풀 때 사용되며, \(A*X + Y = 0\) 형태의 N개의 변수의 N 방정식의 선형 시스템을 풀 때 사용될 수 있습니다. 여기서 A는 NxN 행렬이고, X는 N개의 변수의 벡터, Y는 N개의 상수 벡터입니다.
이 방정식의 직관적인 풀이는 \(X = A^{-1}*(-Y)\)로, 역행렬을 구해서 해를 구할 수 있습니다. 이 방법은 적당한 크기의 행렬에 대해서는 사용할 수 있지만, 행렬의 크기가 크다면 이 방법을 적용하기가 힘듭니다. 게다가 희소행렬의 역행렬을 구하면 0이 아닌 값들이 추가되어 더 이상 희소행렬이 아닐 수 있고, 희소행렬의 역행렬의 보통 원본보다 훨씬 큽니다. 따라서 실제 문제에서 역행렬을 계산하고 저장하는 것은 실용적이지 못합니다.
대신, 희소 행렬로 표현되는 선형 시스템은 반복법(iteration)으로 해를 구할 수 있습니다. 희소행렬 A가 positive(\(X_TAX > 0 for nonzero vector X in \(R^n\))일 때, conjugate gradient method를 사용하여 수렴하는 선형시스템을 반복법으로 해결할 수 있습니다. 만약 결과가 0에 가깝지 않다면, gradient vector formula를 사용하여 예측된 X를 조정하고 \(A*X + Y\) 반복을 다시 수행할 수도 있습니다.
이러한 반복법에서 가장 많은 시간이 소요되는 부분은 \(A*X + Y\)를 계산하는 부분입니다. 아래 그림은 \(A*X + Y\)의 계산을 보여주고, 희소행렬 A의 어두운 사각형은 0이 아닌 원소를 나타냅니다. 반면, X와 Y는 일반적으로 대부분의 원소들이 0이 아닌 값을 가지고 있습니다.
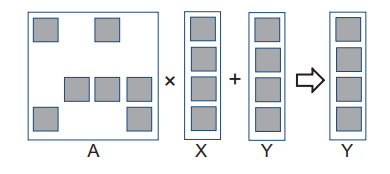
이러한 Sparse Matrix-Vector(SpMV) multiplication and accumulation 이라는 작업을 수행하기 위해 표준화된 라이브러리 함수 인터페이스가 만들어졌는데, 이 SpMV를 사용하여 병렬 희소행렬 계산에서 다른 저장 포맷 간의 장단점을 알아보도록 하겠습니다.
CSR 포맷에 기반한 SpMV의 시퀀셜 코드 구현은 아래 코드처럼 간단합니다. 코드의 자세한 설명은 스킵하도록 하겠습니다 !
void SpMV_CSR_seq(int num_rows, float* data, int* col_index, int* row_ptr, float* x, float* y)
{
for (int row = 0; row < num_rows; row++) {
float dot = 0;
int row_start = row_ptr[row];
int row_end = row_ptr[row+1];
for (int i = row_start; i < row_end; i++)
dot += data[i] * x[col_index[i]];
y[row] += dot;
}
}
CSR 포맷은 저장 공간에 값이 0인 요소들을 모두 제거합니다. col_index와 row_ptr 배열을 사용하면 저장 공간에 오버헤드가 발생할 수 있습니다. Fig.3의 연산에서 행렬 A에는 값이 0인 요소의 수가 그렇지 않은 요소의 수보다 압도적으로 많지 않기 때문에 저장 공간을 절약하는 것보다 오버헤드가 더 큽니다. 그러나 대부분의 원소가 0인 희소행렬의 경우에는 오버헤드보다 절약되는 공간이 훨씬 큽니다. 예를 들어, 전체 원소들 중에 1%만이 0이 아닌 값인 희소행렬에서는 오버헤드를 포함하여 CSR 포맷을 위한 저장공간이 희소행렬 전체를 저장하는데 필요한 공간의 2%만을 차지하게 됩니다.
저장 공간에서 0인 요소들을 모두 제거하면 메모리에서 0인 요소들을 가져오거나 불필요한 곱셈 작업을 수행할 필요가 없습니다. 이 방법을 사용하면 메모리 대역폭과 연산의 리소스 소비를 크게 줄일 수 있습니다.
SpMV 코드에는 사용되는 저장 포맷이 반영됩니다. 위의 코드는 CSR을 사용한 SpMV 코드이므로, 시퀀스 SpMV/CSR이라고 표현하겠습니다.
Parallel SpMV Using CSR
희소행렬의 각 행에 대한 dot product 계산은 다른 행의 dot product와 독립적입니다. 따라서 시퀀스 코드의 각 외부 루프의 반복을 스레드에 할당함으로써 순차적인 SpMV/CSR 코드를 병렬 CUDA 커널로 쉽게 변환할 수 있습니다.
각 스레드는 행렬의 행에 대한 내적(inneer product)을 계산합니다.

Thread 0은 Row 0에 대한 계산, Thread 1은 Row 1에 대한 계산을 담당합니다.
병렬 SpMV/CSR 커널 함수는 아래처럼 구현될 수 있습니다.
__global__
void SpMV_CSR(int num_rows, float* data, int* col_index, int* row_ptr, float* x, float* y)
{
int row = blockDim.x*blockIdx.x + threadIdx.x;
if (row < num_rows) {
float dot = 0;
int row_start = row_ptr[row];
int row_end = row_ptr[row+1];
for (int i = row_start; i < row_end; i++)
dot += data[i] * x[col_index[i]];
y[row] += dot;
}
}시퀀스 코드와 비교하면, 외부 루프가 제거되었습니다. line 4에서는 스레드에 할당된 행 index를 계산하고 있습니다. 그e다음 line 6에서는 if문을 통해 유효한 행들만을 계산하도록 합니다. 그리고 if문 내부에서 스레드에 할당된 하나의 행과 벡터와의 연산을 수행합니다.
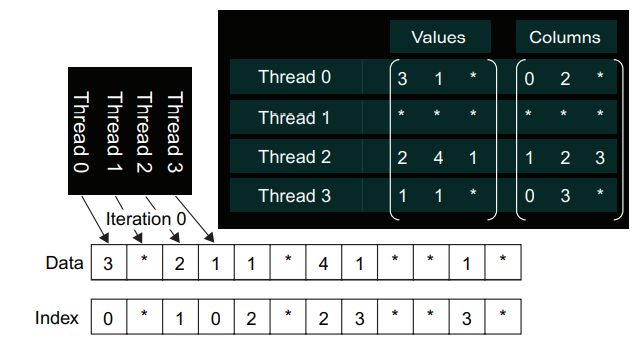
이 커널 함수는 간단하지 두 가지 단점이 있습니다. 첫 번째는 커널이 병합된(coalseced) 메모리 액세스를 하지 않습니다. 위 예제에서는 아래 이미지처럼 첫 번째 반복에서 각 스레드는 data[0], none, data[2], data[5]에 액세스합니다.

그 다음 반복에서 각 스레드는 data[1], none. data[3], data[6]에 액세스하는 식입니다. 따라서 방금 구현한 병렬 SpMV/CSR 커널은 메모리 대역폭을 효율적으로 사용하지 못합니다.
두 번째 단점은 모든 워프에서 상당한 control flow 발산(divergence)가 발생할 수 있다는 것입니다. 각 스레드에서 수행하는 루프의 반복 횟수는 스레드에 할당된 행에 있는 0이 아닌 요소의 수에 따라 달라집니다. 행들 사이에 0이 아닌 원소들의 분포는 무작위적일 수 있기 때문에 인접한 스레드들은 다양한 반복 횟수를 가지게 됩니다. 따라서 대부분 혹은 전체 워프에서 contorl flow 발산이 발생할 수 있습니다.
따라서, 병렬 SpMV 커널의 실행 효율과 메모리 대역폭의 효율은 입력 데이터 행렬의 분포에 따라 달라지게 됩니다. 이러한 경향은 이전까지 살펴본 커널과는 다소 다른데, 이러한 데이터에 의존하는 성능 차이는 실제 어플리케이션에서 흔하게 관찰됩니다.
Padding and Transposition
non-coalesced 메모리 액세스와 분기 발산은 희소행렬 데이터에 데이터 패딩(padding) 및 전치(transposition)을 적용하여 해결할 수 있습니다. 이 아이디어는 elliptic boundary value 문제를 해결하기 위한 패키지인 ELLPACK에서 이름을 따온 ELL 저장 포맷에서 사용됩니다.
ELL 포맷를 이해하기 위해서 먼저 CSR 포맷에서 시작해보겠습니다.

CSR 포맷에서 먼저 0이 아닌 요소의 수가 가장 많은 행을 찾습니다. 그런 다음 찾은 행과 길이가 같도록 요소 뒤에 더미(0) 요소를 추가하여 직사각형 행렬을 생성합니다. 위에서 살펴본 희소행렬 예제에서는 Row 2에서 0이 아닌 요소의 수가 최대이고 이 요소의 수만큼 나머지 행들의 빈 공간에 더미(0)를 추가합니다. Row 0에는 1개의 더미, Row 1에는 3개의 더미, Row 3에는 1개의 더미를 추가하게 됩니다. 이렇게 추가된 더미 요소는 Fig.5의 왼쪽 그림에서 *이 있는 정사각형이고, 이를 추가함으로써 직사각형 행렬을 생성합니다. col_index 배열도 데이터 값에 대한 매핑을 유지하기 위해 같은 방식으로 패딩해야 합니다.
그런 다음 패딩된 행렬을 전치시킵니다. 즉, Row 0의 요소들은 이제 Col 1의 요소가 되고 Row 1의 요소들은 Col 2의 요소들이 됩니다. 이에 맞춰서 col_index의 값들도 데이터 값에 대한 매핑을 유지하기 위해서 유사하게 전치시켜줍니다. 이제 Row i의 시작이 data[i]로 단순화되었기 때문에 row_ptr 배열은 더 이상 필요가 없습니다. 패딩된 요소들을 사용하면 원래 행렬의 Row 수를 더하기만하면 i행의 현재 요소에서 다음 요소로 반복하는 것은 쉽습니다. 아래 Fig.6은 전치된 data 배열과 col_index 배열을 보여줍니다.
아래 코드는 병렬 SpMV/ELL 커널 함수 입니다. SpMV/CSR과는 조금 다른 인수를 전달받는데, 더 이상 row_ptr을 필요로 하지 않습니다. 대신 패딩 후 각 행에 있는 최대 요소의 수를 결정하기 위해서 num_elem 인수가 필요합니다. num_elem는 원래 희소 행렬의 모든 행 중에서 0이 아닌 원소의 최대 수입니다.
__global__
void SpMV_ELL(int num_rows, float* data, int* col_index, int num_elem, float* x, float* y)
{
int row = blockDim.x*blockIdx.x + threadIdx.x;
if (row < num_rows) {
float dot = 0;
for (int i = 0; i < num_elem; i++)
dot += data[row + i*num_rows] * x[col_index[row + i*num_rows]];
y[row] += dot;
}
}
SpMV/ELL 커널의 코드는 SpMV/CSR 커널 코드보다 단순합니다. 패딩을 사용하면 모든 행의 길이가 같아지기 때문에, line 8의 for루프에서 모든 스레드들은 num_elem 값만큼 간단하게 반복할 수 있습니다. 결과적으로 모든 스레드에서 동일한 횟수의 반복을 수행하므로 워프에서의 분기 발산은 더 이상 발생하지 않습니다. 더미 요소가 사용되는 경우에는 값이 0이기 때문에 최종 결과에 영향을 미치지도 않습니다.
두 번째로 루프 내에서 각 스레드는 data[row]의 첫 번째 요소에 액세스하고, 일반적으로 나타내면 data[row + i*num_rows]의 i번째 요소에 액세스합니다. Fig.6에서 볼 수 있듯이 요소를 column major 순서로 배열함으로써 인접한 모든 스레드들이 인접한 메모리 위치에 액세스하여 memory coalescing을 가능하게 합니다. 따라서 메모리 대역폭을 보다 효율적으로 사용할 수 있습니다.
분기 발산을 제거하고 memory coalescing을 활성화함으로써 SpMV/ELL 커널은 SpMV/CSR보다 더 빠르게 실행될 것입니다. 또한 SpMV/ELL이 더 간단하여 모든 측면에서 SpMV/ELL 커널이 더 좋아보입니다.
하지만, SpMV/ELL에는 잠재적인 단점이 있습니다. 하나 또는 소수의 행에서 0이 아닌 요소의 수가 지나치게 많다면, ELL 포맷은 너무 많은 수의 패딩된 요소를 추가합니다. 이러한 요소들은 최종 결과에 영향을 미치지 않음에도 불구하고 저장공간을 너무 많이 차지하게 되고, 또 이 요소들을 읽어오는 데 많은 리소스를 사용하게 됩니다. 위에서 본 간단한 예제를 다시 살펴보면, ELL 포맷에서 우리는 4x4 행렬을 4x3 행렬로 대체했으며, column index의 오버헤드로 원래 4x4 행렬에 포함된 것보다 더 많은 데이터를 저장하고 있습니다.
다른 예제로, 1000x1000의 희소 행렬이 1%의 0이 아닌 요소를 포함한다고 가정해보겠습니다. 평균적으로 각 행에는 10개의 0이 아닌 요소들이 존재하고, CSR 포맷의 경우에 사용되는 저장공간은 전체 크기의 약 2%가 될 것입니다.
만약 행 중에 하나가 0이 아닌 값이 200개이고, 나머지 해을은 10개 미만이라고 가정해봅시다. ELL 포맷을 사용하면 다른 모든 행을 200개의 요소를 가지도록 패딩합니다. 이 방법은 ELL 포맷이 원래 희소행렬 크기의 약 40%의 저장공간을 차지하게 하고, CSR 포맷보다 20배 더 큰 저장공간을 차지합니다.
이렇게 지나치게 긴 행이 있다면 SpMV/CSR 커널에서는 워프 중 하나의 실행시간을 증가시키는 반면, SpMV/ELL 커널은 패딩된 요소 때문에 모든 워프의 실행시간을 증가시킵니다. 이런 문제점 때문에 CSR 포맷에서 ELL 포맷으로 변환할 때 패딩된 요소의 수를 제어하는 방법이 필요합니다.
Using a Hybrid Approach to Regulate Padding
ELL 포맷에서 과도한 패딩의 원인은 하나 또는 소수의 행에서 0이 아닌 요소의 수가 너무 많다는 것입니다. 만약 이 행들에서 일부 요소들을 '제거'하는 메커니즘이 있다면, 우리는 ELL의 패딩된 요소들의 수를 줄일 수 있습니다. Coordinate(COO) 포맷은 이러한 메커니즘을 제공합니다.

COO 포맷은 위 그림에서 보여주고 있습니다. 여기서 0이 아닌 각 요소는 col_index 배열과 row_index 배열과 함께 data 배열에 저장됩니다. 예를 들어, 위에서 살펴본 예제에서 A[0,0]=3은 col_index[0]=0과 rowl_index[0]=0과 함께 저장됩니다. COO 포맷을 사용하면 저장 공간의 어떠한 요소들도 살펴볼 수 있고 그 요소가 원래 희소행렬에서 어디에 위치하는 지도 알 수 있습니다. ELL 포맷의 경우와 마찬가지로 row_ptr은 필요없습니다.
COO 포맷은 row_index 배열에 대한 추가적인 저장공간이 필요하지만 유연성이라는 이점을 제공합니다. 아래 Fig.8과 같이 data, col_index, row_index 배열의 순서를 변경해도 COO 포맷은 요소의 정보를 잃지 않기 때문에 임의로 순서를 변경할 수 있습니다.

Fig.8에서 data, col_index, row_index의 요소들을 재정렬했습니다. 현재 data[0]에는 Row 3, Col 0의 요소의 값이 저장되어 있습니다. 이처럼 data의 값을 row_index와 col_index 값과 함께 이동하여 원래 희소행렬에서의 위치를 올바르게 식별할 수 있습니다.
이러한 재정렬은 메모리 대역폭의 효율적인 사용에 필요한 위치와 순차적인 패턴을 방해할 수 있는데, 왜 요소들을 재정렬할까요 ?
이에 대한 답은 COO 포맷을 사용하는 케이스에 있습니다. COO 포맷은 CSR 포맷이나 ESS 포맷의 행 길이를 제한하는데 사용할 수 있습니다. COO 포맷에서는 원하는 순서로 요소들을 처리할 수 있습니다. data[i]의 각 요소들은 간단하게 y[row_index[i]] += data[i] * x[col_index[i]] 연산을 통해 계산될 수 있고, 모든 데이터 요소에 대해 이 연산을 수행하면 처리되는 순서에 관계없이 정확한 최종값을 얻을 수 있습니다.
희소 행렬을 CSR 포맷이나 ELL 포맷으로 변환하기 전에 0이 아닌 요소가 매우 많은 행에서 일부 요소들을 제거하고 별도의 COO 저장 공간에 배치할 수 있습니다. 남은 요소들은 SpMV/ELL을 사용하면 됩니다. 이렇게 함으로써 패딩되는 요소의 수를 상당히 줄일 수 있고, SpMV/COO를 사용하여 작업을 완료하면 됩니다.
구구절절 설명했지만, 요약하면 ELL 포맷과 COO 포맷을 함께 사용하는 것입니다. 이런 방식을 hybrid method라고 합니다.
SpMV를 위한 Hybrid ELL, COO 방법을 아래 이미지에서 잘 보여주고 있습니다.
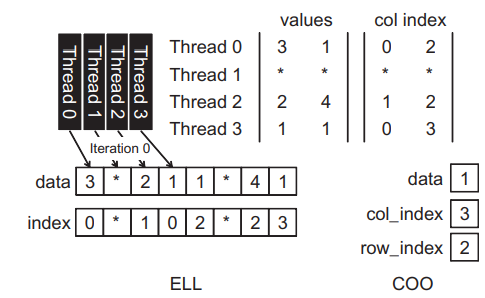
Row 2에서 0이 아닌 원소의 수가 가장 많은데, 우리는 ELL 포맷에서 Row 2의 마지막 요소를 제거하고 별도의 COO 포맷으로 이동시킵니다. Row 2의 제거된 마지막 요소 덕분에 모든 행 중에서 0이 아닌 요소의 최대 갯수가 3개에서 2개로 줄어 들고, Fig.9와 같이 패딩된 요소의 수가 5개에서 2개로 감소하게 됩니다. 더 중요한 것은 모든 스레드의 for루프 반복 횟수가 3회에서 2회로 감소되기 때문에 SpMV/ELL 커널의 병렬 실행을 50% 가속화할 수 있습니다.
ELL-COO hybrid를 사용하는 일반적인 방법은 host에서 CSR 포맷과 유사한 포맷을 ELL 포맷으로 변환하는 것입니다. 변환하는 동안 host는 non-zero 요소들이 너무 많은 행에서 일부 요소들을 제거합니다. Host는 이러한 요소들을 COO 포맷의 저장공간으로 이동시킨 다음 ELL 포맷의 데이터를 device로 전달합니다. Device에서 SpMV/ELL 커널 수행을 완료하면 다시 결과값 y를 host로 전달하는데, 이 값에는 COO 포맷에 있는 요소들의 결과는 누락되어 있습니다. Host는 COO 포맷의 요소들에 대해 순차적인 SpMV/COO 커널을 수행하고 최종 결과에 더해줍니다.
Host에서 요소들을 ELL 포맷에서 COO 포맷으로 분리하기 위해 수행하는 추가 작업에서 과도한 오버헤드가 발생하는지에 대한 여부를 의심할 수 있습니다. 하나의 SpMV 계산에만 희소행렬이 사용되는 경우에는 이러한 추가 작업이 실제로 상당한 오버헤드를 발생시킬 수 있습니다. 하지만, 실제 어플리케이션에서는 동일한 반복하는 solver에 의해 동일한 희소 커널에서 SpMV가 수행되고, solver의 각 반복에서 x와 y벡터는 다양하지만 희소 행렬은 선형 시스템의 계수에 해당하기 때문에 동일합니다. 따라서, ELL-COO hybrid에서 ELL 포맷과 COO 포맷의 데이터를 생성하는 작업은 반복되지 않고 한 번만 수행되므로 오버헤드가 상각될 수 있습니다.
ELL 포맷에서의 SpMV/ELL 커널 코드는 위에서 살펴봤고, 나머지 COO 포맷에 의한 연산은 다음과 같을 것입니다.
void SpMV_COO_seq(float* data, int* col_index, int* row_index, int num_elem, float* x, float* y)
{
for (int i = 0; i < num_elem; i++)
y[row_index[i]] += data[i] * x[col_index[i]];
}루프는 매우 간단합니다. 모든 데이터 요소들에 대해 반복을 수행하고 col_index와 row_index의 값들을 사용하여 적절한 x, y 요소에 대해 곱셈 및 누적 연산을 수행합니다.
병렬 SpMV/COO 커널은 atomic 연산을 사용하여 아래처럼 구현할 수 있습니다. 더 이상 스레드가 특정 행에 매핑되는 것이 아니기 때문에 한 스레드당 하나의 data를 처리하도록 하면 됩니다.
__global__
void SpMV_COO(float* data, int* col_index, int* row_index, int num_elem, float* x, float* y)
{
int i = blockDim.x*blockIdx.x + threadIdx.x;
if (i < num_elem) {
float dot;
dot = data[i] * x[col_index[i]];
atomicAdd(&y[row_index[i]], dot);
}
}하지만, CPU의 대용량 캐시 메모리를 사용하여 SpMV/COO를 연산하는 것이 더 빠를 것입니다.
hybrid SpMV/ELL-COO 방법은 이기종 컴퓨팅 시스템에서 CPU와 GPU의 활용을 보여줍니다. CPU는 SpMV/COO를 쉽게 수행할 수 있고, GPU는 병합된 메모리 액세스와 많은 수의 코어를 사용하여 SpMV/ELL을 빠르게 수행할 수 있습니다.
ELL 포맷에서 몇몇의 요소들을 제거하는 것을 정규화(regularization) 기법이라고 합니다.
수행 결과
지금까지 살펴본 CSR / ELL / Hybrid ELL-COO 방법들을 실제 코드로 실행하여 성능을 비교해보겠습니다.
임의로 행렬의 요소 중에 0의 비율을 설정하여 행렬과 벡터 X,Y를 초기화했고, 총 100번의 연산의 평균 시간을 측정하였습니다. 100번의 연산 전에 각 포맷으로 처음 한 번 변환하는 시간도 포함을 하여, 약간이나마 객관적인 수행 시간을 측정하도록 했습니다.
전체 코드는 아래 링크를 참조하시길 바랍니다.
GitHub - junstar92/parallel_programming_study: Study parallel programming - CUDA, OpenMP, MPI, Pthread
Study parallel programming - CUDA, OpenMP, MPI, Pthread - GitHub - junstar92/parallel_programming_study: Study parallel programming - CUDA, OpenMP, MPI, Pthread
github.com
각 방법들로 8192 x 8192 Sparse Matrix와 8192개의 요소들을 갖는 벡터 X, Y의 연산을 수행했습니다.
먼저 희소 행렬에서 0의 요소 비율을 20%로 설정했을 때의 결과입니다.

보통의 행렬을 위한 저장 공간이 256MB가 필요한 반면, 각 포맷으로 변환하면, CSR 포맷의 경우에는 101MB, ELL 포맷의 경우에는 110MB, Hybrid ELL-COO의 경우 120MB가 필요했습니다.
(Hybrid ELL-COO의 경우 한 행에서의 최대 요소의 개수를 N / 8로 설정하여 위 경우에는 1024개로 설정되어 있습니다.)
수행 시간은 ELL - CSR - Hybrid ELL/COO - Sequential CSR 순으로 빨랐습니다.
0인 요소의 비율을 10%로 줄여서 다시 연산을 수행해보겠습니다.

전체적인 연산 속도를 빨라졌지만, 이중에서는 CSR 포맷이 가장 빠른 속도를 보여주고 있습니다. 특히 저장 공간도 50MB로 3개의 포맷 중에 가장 적은 저장 공간을 차지하고 있습니다.
'NVIDIA > CUDA' 카테고리의 다른 글
| Graph Search (Breadth-First Search) (0) | 2021.12.30 |
|---|---|
| Parallel Merge Sort (merge operation) (0) | 2021.12.24 |
| Parallel Histogram (0) | 2021.12.18 |
| Parallel Prefix Sum (2) (0) | 2021.12.17 |
| Parallel Prefix Sum (1) (0) | 2021.12.15 |




댓글