References
- Programming Massively Parallel Processors
Contents
- A Sequential Merge Algorithm
- A Parallelization Approach : co-rank
- CO-RANK function Implementation
- A Basic Parallel Merge Kernel
- A Tiled Merge Kernel
- A Circular-Buffer Merge Kernel
이번 포스팅에서 살펴 볼 병렬 패턴은 ordered merge operation 입니다. 이는 두 개의 정렬된 리스트를 받아서 하나의 정렬된 리스트를 생성합니다. Ordered merge operation은 정렬 알고리즘으로 사용될 수 있습니다. 정렬은 컴퓨터 공학의 수 많은 분야에서 중요하고 고전적인 문제입니다. 또한, Ordered merge operation은 현재 map-reduce 프레임워크의 기본을 형성합니다.
Ordered merge operation은 병렬화를 위한 분할 정복 접근의 좋은 예제이며, 이번 포스팅에서 각 스레드의 입력 데이터가 동적으로 결정되는 parallel ordered merge 알고리즘을 살펴보겠습니다. 데이터 액세스가 동적으로 이루어지기 때문에 메모리 액세스 효율성 및 성능 향상을 위한 locality(지역성)을 활용하기가 어려운데, 메모리 액세스 효율을 높이기 위해서 어떠한 작업이 필요한지도 알아보겠습니다.
Background
Ordered merge function은 두 개의 정렬된 리스트 A와 B를 전달받아서, 이들을 정렬된 리스트 C로 합칩니다. 간단하게 살펴보기 위해서 이미 정렬된 리스트를 입력으로 사용하겠습니다.
아마 Merge Sort는 익숙하실거라고 생각됩니다. 재귀적으로 배열을 하나의 요소가 남을 때까지 쪼갠 후에 두 정렬된 두 배열을 정렬된 순서로 Merge시키는 정렬 알고리즘인데, 우리는 두 개의 정렬된 배열을 하나의 정렬된 배열로 합치는 merge operation에 대해서 포커스를 맞추도록 하겠습니다.
아래 그림은 간단한 merge function의 수행을 보여줍니다.

두 개의 정렬된 배열 A, B가 합쳐져서 9개의 정렬된 하나의 배열 C를 생성합니다.
Merge Operation은 병렬 병합 정렬(Merge Sort)의 핵심입니다. 병렬 병합 정렬 함수는 입력 리스트를 여러 섹션으로 나누고 병렬 스레드에 분배하고, 스레드는 각각의 섹션을 정렬한 후에 정렬된 섹션을 공동으로 병합합니다. 이렇게 분할 정복 접근은 정렬의 효율적인 병렬화를 가능하게 합니다.
하둡(Hadoop)과 같은 현대 map-reduce 분산 컴퓨팅 프레임워크에서 연산은 엄청난 수의 컴퓨터 노드에 분산됩니다. reduce 프로세스는 각 컴퓨터 노드들의 결과를 하나의 결과로 통합합니다. 많은 응용프로그램에서는 결과를 순서 관계에 따라서 정렬하도록 요구하기도 하는데, 이러한 결과는 일반적으로 reduce tree 패턴의 merge operation을 사용하여 통합됩니다. 따라서 효율적인 merge oepration은 이러한 프레임워크의 효율성 측면에서 매우 중요합니다.
A Sequential Merge Algorithm
Merge operation은 간단한 시퀀스(순차) 알고리즘으로 구현될 수 있습니다. 아래 코드는 순차 병합 연산을 수행하는 함수입니다.
void sequentialMerge(int* A, int nA, int* B, int nB) { int *tmpA, *tmpB; tmpA = (int*)malloc(nA*sizeof(int)); tmpB = (int*)malloc(nB*sizeof(int)); for (int i = 0; i < nA; i++) tmpA[i] = A[i]; for (int i = 0; i < nB; i++) tmpB[i] = B[i]; int *C = A; int iA = 0, iB = 0, iC = 0; while ((iA < nA) && (iB < nB)) { if (tmpA[iA] <= tmpB[iB]) { C[iC++] = tmpA[iA++]; } else { C[iC++] = tmpB[iB++]; } } if (iA == nA) { while (iB < nB) C[iC++] = tmpB[iB++]; } else { while (iA < nA) C[iC++] = tmpA[iA++]; } free(tmpA); free(tmpB); }
일반적인 병합 정렬은 in-place로 정렬이 이루어지기 때문에, 이 함수에서는 배열 A와 B가 서로 붙어있다고 가정하고, A의 시작주소를 사용하여 A와 B의 메모리 공간을 갖는 C를 사용하여 병합합니다. 병합 정렬은 일반적으로 추가적인 메모리 공간이 필요한데, in-place로 정렬이 수행되므로, 원본 배열의 정보를 저장하기 위한 tmpA와 tmpB를 새로 할당하여 사용하고 있습니다. 사용이 끝난 tmpA와 tmpB는 함수가 리턴되기 전에 메모리가 해제됩니다.
위의 순차 함수는 두 개의 주요 부분으로 구성됩니다. 첫 번째 부분은 line 14-22인데, while 루프를 통해 A와 B의 요소들을 순서대로 방문합니다. 루프의 첫 시작은 A[0]과 B[0]으로부터 시작하고, 매 루프마다 A 요소와 B 요소 중에 더 작은 값을 output 배열 C의 한 요소에 채웁니다.
while 루프는 배열 A나 B의 끝에 다다를때까지 수행되고, while 루프가 종료되면 두 번째 부분을 수행합니다. 두 번째 부분은 이어지는 line 24-31이며, 만약 배열 A를 모두 방문했다면 배열 B의 나머지 요소들을 배열 C에 위치시키고, 배열 B를 모두 방문했다면 배열 A의 나머지 요소들을 배열 C에 위치시킵니다.
함수가 수행되면 Fig.1처럼 두 배열이 하나의 배열로 병합됩니다.
순차 병합 함수는 A와 B의 모든 요소를 한 번씩 방문하고 그 값을 배열 C에 한 번씩 씁니다. 알고리즘의 시간복잡도는 O(m+n)이며, 실행 시간은 병합할 요소의 총 수에 선형적으로 비례합니다.
A Parallelization Approach
그렇다면 병합 연산은 어떻게 병렬화할 수 있을까요?
Siebert의 논문에서 병합 연산을 병렬화하는 접근방식을 제안했습니다.
이 방식에서 각 스레드는 먼저 output 위치의 범위(출력 범위)를 먼저 계산하고, 이 output 범위를 co-rank 함수의 입력으로 사용하는데, 이 co-rank 함수는 output 범위를 생성하기 위해 병합되는 대응하는 입력 범위를 식별합니다.
입력과 출력의 범위가 결정되면, 각 스레드는 독립적으로 두 입력의 subarray와 하나의 출력 subarray에 액세스합니다. 이러한 독립성은 각 스레드가 그들의 subarray에서 순차 병합 함수를 수행하여 병합을 병렬적으로 수행할 수 있도록 합니다. 이 방법의 핵심은 co-rank function 입니다.
그럼 co-rank function에 대해 알아보겠습니다.
각각 m, n개로 이루어진 입력 배열 A, B가 있고, 두 배열은 이미 정렬이 되어 있다고 가정하겠습니다. 각 배열의 인덱스는 0부터 시작합니다. 그리고 A와 B를 병합하여 생성되는 정렬된 출력 배열이 C라고 한다면 C는 m+n개의 요소들로 구성될 것 입니다.
먼저 다음과 같은 이미지의 경우를 살펴보겠습니다.

위 그림에서 C[4] (value 9)는 A[3]의 값으로부터 전달받습니다. 이 경우 k=4이고 i=3입니다. 여기서 C[4] 앞에 오는 4 elements의 subarray C[0]-C[3]은 A[3] 앞에 오는 3 elements의 subarray A[0]-A[2]와 B[1] 앞에 오는 (4 - 3 = 1) element의 subarray B[0]의 merge 결과입니다.
공식을 일반화하면, k개의 요소를 가진 subarray C[0]-C[k-1]은 i개의 요소를 가진 subarrya A[0]-A[i-1]와 (k-i)개의 요소를 가진 subarray B[0]-B[k-i-1]의 merge 결과입니다.
아래의 경우를 한번 더 살펴보겠습니다.

이 경우 C[6]은 B[1]로부터 값을 전달받습니다. k=6이고, j=1이 됩니다. C[6] 앞에 오는 subarray C[0]-C[5]는 A[5]의 앞에 위치한 subarray A[0]-A[4]와 B[1]의 앞에 위치한 subarray B[0]의 merge 결과입니다.
첫 번째 경우, 우리는 i의 값을 찾았고, k-i를 통해서 j의 값을 유도했습니다. 두 번째 경우에는 j의 값을 먼저 찾고, k-j를 통해 i의 값을 유도했습니다. 따라서, 우리는 대칭성을 이용하여 두 경우를 다음과 같이 정리할 수 있습니다.
를 만족하는 어떠한 k에서, , , and 을 만족하는 i와 j를 찾을 수 있고, subarray C[0]-C[k-1]은 subarray A[0]-A[i-1]과 subarray B[0]-B[j-1]의 merge 결과이다.
또한, Siebert는 길이가 k인 prefix subarray C를 생성하는데 필요한 A와 B의 prefix subarray를 정의하는 i와 j는 유일하다라는 것을 증명했습니다.
C[k] 요소에서, 인덱스 k는 이들의 rank이며, 유일한 인덱스인 i와 j를 이들의 co-rank라고 합니다.
위에서 살펴본 첫 번째 케이스에서 C[4]의 rank와 co-rank는 각각 4, 3, 1이고, 두 번째 케이스에서 C[6]의 rank와 co-rank는 각각 6, 5, 1이 됩니다.
co-rank의 개념은 merge function을 병렬화할 수 있는 길을 제공합니다. 각 스레드 별로 출력 배열을 나누어서 할당하고, 각 스레드에 할당된 subarray를 생성하도록 할당할 수 있습니다. 할당이 완료되면, 각 스레드에 의해 생성된 output 요소의 rank를 알 수 있고, 그러면 각 스레드는 co-rank 함수를 사용하여 출력 subarray에 merge 해야하는 입력 배열의 subarray를 결정할 수 있습니다.
이전에 살펴본 히스토그램과 이번 포스팅의 병합 함수와의 주요한 차이점은 각 스레드가 사용할 입력의 범위를 간단하게 결정할 수 없다는 것입니다. 각 스레드가 사용할 입력 요소의 범위는 co-rank 함수에 의해서 결정됩니다.
CO-RANK Function Implementation
co-rank 함수는 C 배열 요소의 rank (k)와 두 입력 배열의 정보를 파라미터로 전달받아서 i co-rank 값을 리턴하는 함수로 정의할 수 있습니다.
int co_rank(int k, int* A, int m, int* B, int n);여기서 k는 C 요소의 rank이고, A는 입력 배열 A의 포인터, m은 배열 A의 크기, B는 입력 배열 B의 포인터, n은 배열 B의 크기입니다. co-rank i의 값을 구하면 j는 k-i를 통해서 유도할 수 있습니다.
co-rank 함수의 자세한 구현을 살펴보기 전에 parallel merge function이 이것을 사용하는 방법에 대해서 먼저 이야기해보겠습니다.
아래 그림에서는 두 개의 스레드를 사용하여 병합 연산을 수행하는 것을 보여줍니다.
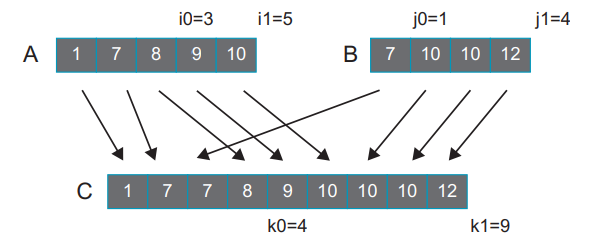
여기서 스레드 0은 C[0]-C[3]을 생성하고, 스레드 1은 C[4]-C[8]을 생성한다고 가정해보겠습니다.
스레드 0은 co-rank function을 호출하여, co-rank 값인 i0=3, j0=1을 얻을 수 있습니다. 즉, C[4]의 prefix subarray(C[0]-C[3])는 A[3]의 prefix subarray(A[0]-A[2])와 B[1]의 prefix subarray(B[0])의 병합의 결과로 생성됩니다. 직접 살펴보면 아시겠지만, i0=3과 j0=1이 적절하고 정확하다는 것을 알 수 있습니다.
스레드 1이 co-rank 함수를 호출하면 co-rank 함수로부터 co-rank의 값이 i1=5, j1=4라는 것을 알 수 있습니다. 하지만 스레드 1에 의해 사용되는 입력 subarray(A[3]-A[4], B[1]-B[3])는 스레드 0의 co-rank의 값과 스레드 1의 co-rank의 값에 의해서 정의됩니다. 즉, 스레드 1에 대한 A의 subarray의 시작 인덱스는 스레드 0의 co-rank i의 값입니다. 스레드 1에서 B의 subarray의 시작 인덱스는 스레드 0의 co-rank j의 값이 됩니다.
일반적으로, 스레드 t에서 사용되는 입력 subarray는 스레드 (t-1)과 스레드 t에 의해서 정의됩니다.
: - and -
한 가지 중요한 점은 큰 입력 배열에서 각 스레드 별로 co-rank를 찾는 작업을 스레드마다 크게 다를 수 있다는 것입니다. 출력 배열의 시작 부분을 생성하는 스레드는 적은 수의 A와 B 요소들을 통해 찾을 수 있지만, 높은 번호를 가진 스레드들은 많은 수의 A, B 요소들을 검색해야할 수 있습니다. 따라서 많은 수의 요소들을 찾을 때의 지연 시간을 최소화하는 것이 매우 중요합니다. 우리는 두 입력 배열의 정렬되어 있다고 가정하기 때문에 이진 탐색(binary search)이나 higher radix search를 사용하여 계산 복잡도를 O(N)에서 O(logN)으로 줄일 수 있습니다.
아래 코드는 출력 배열의 rank k에 대응되는 배열 A의 co-rank i를 반환하는 co-rank 함수입니다.
int co_rank(int k, int* A, int m, int* B, int n) { int i = (k < m) ? k : m; // i = min(k, m); int j = k-i; int i_low = (0 > (k-n)) ? 0 : k-n; // i_low = max(0, k-n); int j_low = (0 > (k-m)) ? 0 : k-m; // j_low = max(0, k-m); int delta; bool active = true; while (active) { if (i > 0 && j < n && A[i-1] > B[j]) { delta = ((i - i_low + 1) >> 1); j_low = j; j = j + delta; i = i - delta; } else if (j > 0 && i < m && B[j-1] >= A[i]) { delta = ((j - j_low + 1) >> 1); i_low = i; i = i + delta; j = j - delta; } else { active = false; } } return i; }
co-rank 함수는 두 쌍의 마커 변수를 사용하여 co-rank 값인 A의 배열 인덱스 범위와 B의 배열 인덱스 범위를 계산합니다. i_low와 j_low 변수는 함수에 의해 생성될 수 있는 가장 작은 co-rank 값입니다. 그리고 변수 i와 j는 현재 루프에서 co-rank라고 추정하는 값입니다.
co-rank 함수의 자세한 설명은 스킵하도록 하겠습니다. 중요한 것은 co-rank 함수를 통해서 output 배열의 subarray를 생성하기 위한 배열 A와 B의 subarray 범위를 계산할 수 있습니다.
A Basic Parallel Merge Kernel
이제 병렬 merge operation 커널 함수를 살펴보겠습니다. input 배열 A와 B는 전역 메모리에 위치한다고 가정합니다.
__global__ void merge_basic_kernel(int* A, int m, int* B, int n, int* C) { int tid = blockDim.x*blockIdx.x + threadIdx.x; int k_curr = tid * ceil((m+n)/(float)(blockDim.x*gridDim.x)); int k_next = min((tid+1) * (int)ceil((m+n)/(float)(blockDim.x*gridDim.x)), m+n); int i_curr = co_rank(k_curr, A, m, B, n); int i_next = co_rank(k_next, A, m, B, n); int j_curr = k_curr - i_curr; int j_next = k_next - i_next; sequentialMerge(A+i_curr, i_next-i_curr, B+j_curr, j_next-j_curr, C+k_curr); }
위 커널 함수는 두 입력 배열을 병합하여 새로운 출력 배열 C를 생성합니다. 배열 C도 역시 전역 메모리에 위치합니다. 보다시피, 커널 함수는 매우 심플합니다. 각 스레드에서 출력 배열의 subarray의 시작 지점(k_curr)을 계산하고, 다음 출력 배열의 subarray의 시작 지점(k_next)를 계산합니다. 그리고 k_curr과 k_next로 co_rank 함수를 각각 호출하여 co-rank 값을 계산합니다. k_curr에 의해 호출된 co_rank 함수는 현재 스레드에 의해 생성되는 출력 subarray의 첫 번째 요소의 co-rank 값입니다. 함수로부터 반환받은 co-rank 값으로부터 스레드에서 사용되는 입력 배열 A와 B의 subarray의 첫 번째 인덱스를 계산할 수 있습니다. 코드에서 i_curr과 j_curr 값이 바로 스레드에서 사용되는 입력 subarray의 첫 번째 인덱스 값입니다. 따라서 A+i_curr과 B+j_curr은 현재 스레드에 의해 사용되는 입력 subarray의 시작 지점의 주소입니다.
k_next를 사용하여 호출된 co_rank는 다음 스레드의 co-rank 값을 계산합니다. 즉, 다음 스레드에 의해서 사용되는 입력 subarray의 첫 번째 인덱스 값을 계산합니다.
그러므로, i_next - i_curr과 j_next - j_curr은 현재 스레드에서 사용되는 A와 B의 subarray의 크기(m, n)이 됩니다. 이제 처음에 살펴본 sequentialMerge를 호출하기 위해 필요한 정보들을 다 구했고, 마지막으로 sequentialMerge 함수를 호출하면 됩니다.
간단하게, 정렬된 두 배열 A, B를 merge operation으로 병합해봤습니다. 순차적으로 수행하는 것과 CUDA를 사용한 병렬 수행을 둘 다 실행했는데, 그 결과는 다음과 같습니다.
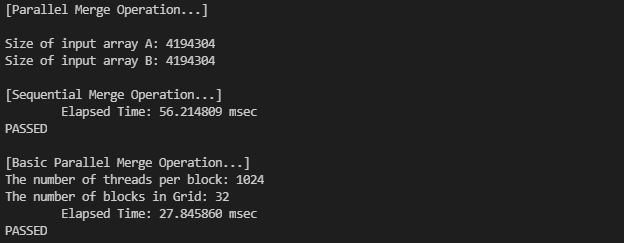
두 배열의 크기 m과 n이 각각 4,194,304이고, 출력 배열의 크기는 m+n=8,388,608이 되겠죠.
결과는 32개의 블록과 블록당 스레드의 수를 1024개로 설정한 병렬 수행이 순차 수행보다 약 2배 정도 더 빠르게 수행되고 있습니다.
사용된 코드는 아래 링크에서 확인하실 수 있습니다.
https://github.com/junstar92/parallel_programming_study/blob/master/CUDA/mergeSort/mergeOperation.cu
GitHub - junstar92/parallel_programming_study: Study parallel programming - CUDA, OpenMP, MPI, Pthread
Study parallel programming - CUDA, OpenMP, MPI, Pthread - GitHub - junstar92/parallel_programming_study: Study parallel programming - CUDA, OpenMP, MPI, Pthread
github.com
A Tiled Merge Kernel
위에서 살펴본 basic merge kernel은 단순히 전역 메모리만을 사용하고 있습니다. 따라서 공유 메모리를 사용하여 merge kernel의 메모리 액세스 패턴을 한 번의 액세스로 병합하는 패턴으로 변경할 수 있습니다.
인접한 스레드들에 의해서 사용되는 입력 배열 A와 B의 subarray는 메모리에서 서로 인접하다는 것을 볼 수 있습니다. 블록 내의 모든 스레드들은 서로 협력하여 블록 레벨의 A와 B의 subarray를 사용하여 블록 레벨의 출력 subarray C를 생성할 수 있습니다. 블록 레벨에서 A와 B의 subarray의 co-rank 또한 co_rank 함수를 통해 얻을 수 있고, 이러한 블록 레벨의 co-rank 값을 사용하여 블록의 모든 스레드들을 협력하여 블록 레벨의 A와 B의 subarray를 병합 패턴으로 공유 메모리에 적재할 수 있습니다.
아래 그림은 Tiled Merge Kernel의 블록 레벨 디자인을 보여주고 있습니다. 이 그림에서는 merge operation에 3개의 블록이 사용된다고 가정합니다.
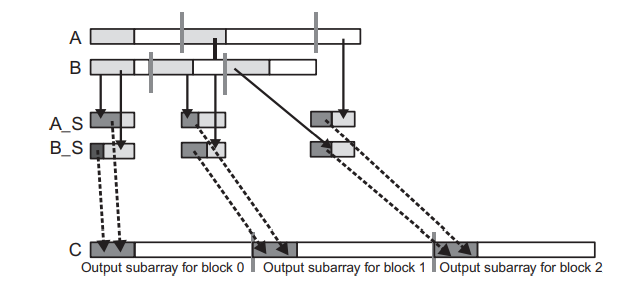
그림 아래쪽에 출력 배열 C는 3개의 블록 레벨의 subarray로 분할됩니다. 이렇게 분할된 각 블록은 사용할 입력의 subarray를 구하기 위해서 co-rank 함수를 호출합니다. 여기서 입력 subarray의 크기는 실제 데이터 값에 따라 크게 달라질 수 있는데, 위 예시에서 스레드 0의 A의 subarray의 크기는 B의 subarray의 크기보다 훨씬 큽니다.
Tiled Merge Kernel에서 각 블록에 대해 두 개의 공유 메모리 배열 A_S와 B_S를 선언할 것입니다. 제한된 공유 메모리 크기 때문에 A_S와 B_S는 블록에서 사용되는 입력 subarray 전체를 포함하지 못할 수 있습니다. 따라서, 우리는 반복적인 접근을 취해야 합니다.
각 출력 subarray가 y개의 요소를 포함하는 동안, A_S와 B_S는 각 x개의 요소를 hold할 수 있다고 가정합니다. 각 스레드 블록은 번의 반복을 수행하는데, 반복하는 동안 블록의 모든 스레드는 서로 협력하여 A의 subarray에서 x개의 요소와 B의 subarray에서 x개의 요소를 A_S와 B_S로 로드합니다.
각 스레드에서의 첫 번째 반복은 위 그림에서 보여주고 있습니다. A와 B 배열의 subarray에서 회색으로 밝게 칠해진 부분이 A_S와 B_S로 로드되고 있습니다. 공유 메모리에 x개의 A요소와 x개의 B요소가 있는 스레드 블록은 적어도 x개의 출력 배열 요소를 생성하기에 충분한 요소를 가지고 있고, 모든 스레드는 반복에 필요한 모든 입력의 subarray 요소를 갖출 수 있습니다.
여기서 A와 B에서 각각 x개씩 2x개의 입력 요소를 공유 메모리로 로드했는데, x개의 출력 요소의 생성만을 보장할 수 있는지 궁금할 수 있는데, 최악의 경우에는 현재 출력 subarray의 모든 요소가 입력 subarray 중의 하나에서 나올 수 있기 때문입니다. 이러한 불확실성 때문에 Merge Kernel에 대한 타일링 설계는 다른 예제보다 어렵습니다.
Fig.2는 각 블록의 스레드가 C의 subarray에서 x개의 요소로 구성된 섹션을 생성하기 위해 각 반복에서 A_S의 일부와 B_S의 일부를 사용하는 것을 보여줍니다. 이 과정은 A_S와 B_S에서 짙은 회색으로 칠해진 부분이 C로 이동하는 것입니다. 어떤 블록은 A_S의 요소를 더 많이 사용할 수 있고, 다른 블록은 B_S의 요소를 더 많이 사용할 수 있는데, 각 블록에서 사용되는 요소의 비율은 입력 데이터 값에 따라서 달라집니다.
아래 코드는 타일링을 적용한 merge opereation 커널 함수를 보여줍니다. 꽤나 길지만, 천천히 살펴보도록 하겠습니다.
__global__ void merge_tiled_kernel(int* A, int m, int* B, int n, int* C, int tile_size) { /* Part 1 : Identifying block-level output and input subarrays */ extern __shared__ int shareAB[]; int* A_S = shareAB; int* B_S = shareAB + tile_size; int C_curr = blockIdx.x * ceil((m+n)/(float)gridDim.x); int C_next = min((blockIdx.x+1) * (int)ceil((m+n)/(float)gridDim.x), m+n); if (threadIdx.x == 0) { A_S[0] = co_rank(C_curr, A, m, B, n); A_S[1] = co_rank(C_next, A, m, B, n); } __syncthreads(); int A_curr = A_S[0]; int A_next = A_S[1]; int B_curr = C_curr - A_curr; int B_next = C_next - A_next; __syncthreads(); int counter = 0; int C_length = C_next - C_curr; int A_length = A_next - A_curr; int B_length = B_next - B_curr; int total_iteration = ceil((C_length)/(float)tile_size); int C_completed = 0; int A_consumed = 0; int B_consumed = 0; while (counter < total_iteration) { /* Part 2 : Loading A and B elements into the shared memory */ // loading tile-size A and B elements into shared memory for (int i = 0; i < tile_size; i += blockDim.x) { if (i + threadIdx.x < A_length - A_consumed) A_S[i + threadIdx.x] = A[A_curr + A_consumed + i + threadIdx.x]; } for (int i = 0; i < tile_size; i += blockDim.x) { if (i + threadIdx.x < B_length - B_consumed) B_S[i + threadIdx.x] = B[B_curr + B_consumed + i + threadIdx.x]; } __syncthreads(); /* Part 3 : All threads merge their individual subarrays in parallel */ int c_curr = threadIdx.x * (tile_size/blockDim.x); int c_next = (threadIdx.x+1) * (tile_size/blockDim.x); c_curr = (c_curr <= C_length - C_completed) ? c_curr : C_length - C_completed; c_next = (c_next <= C_length - C_completed) ? c_next : C_length - C_completed; // find co-rank for c_curr and c_next int a_curr = co_rank(c_curr, A_S, min(tile_size, A_length-A_consumed), B_S, min(tile_size, B_length-B_consumed)); int b_curr = c_curr - a_curr; int a_next = co_rank(c_next, A_S, min(tile_size, A_length-A_consumed), B_S, min(tile_size, B_length-B_consumed)); int b_next = c_next - a_next; // All threads call the sequential merge function sequentialMerge(A_S + a_curr, a_next - a_curr, B_S + b_curr, b_next - b_curr, C + C_curr + C_completed + c_curr); // Update the A and B elements that have been consumed thus far counter++; C_completed += tile_size; A_consumed += co_rank(tile_size, A_S, tile_size, B_S, tile_size); B_consumed = C_completed - A_consumed; __syncthreads(); } }
커널 함수는 크게 3개의 파트으로 나눌 수 있습니다.
첫 번째 파트은 블록 레벨에서의 출력 배열의 시작과 끝 인덱스를 계산하고, 이에 대한 co-rank 값을 계산합니다. 이때, co-rank의 값은 블록의 모든 스레드에서 접근할 수 있도록 값을 공유 메모리에 저장합니다. 이 계산은 하나의 스레드에서만 co-rank 함수를 호출하면 되고, __syncthreads 함수를 통해 co-rank 값이 다 계산되고 난 뒤에 모든 스레드에서 사용할 수 있도록 해줍니다.
/* Part 1 : Identifying block-level output and input subarrays */ extern __shared__ int shareAB[]; int* A_S = shareAB; int* B_S = shareAB + tile_size; int C_curr = blockIdx.x * ceil((m+n)/(float)gridDim.x); int C_next = min((blockIdx.x+1) * (int)ceil((m+n)/(float)gridDim.x), m+n); if (threadIdx.x == 0) { A_S[0] = co_rank(C_curr, A, m, B, n); A_S[1] = co_rank(C_next, A, m, B, n); } __syncthreads(); int A_curr = A_S[0]; int A_next = A_S[1]; int B_curr = C_curr - A_curr; int B_next = C_next - A_next; __syncthreads();
방금 전에도 언급했지만, 입력의 subarray가 너무 커서 공유 메모리 크기에 맞지 않을 수 있습니다. 따라서, 커널은 반복적인 접근법으로 수행됩니다. 커널 함수는 공유 메모리에 적재될 A 요소의 수와 B 요소의 수를 결정하는 tile_size라는 인수를 전달받습니다. 예를 들어, tile_size의 값이 1024라면 1024개의 A 요소와 1024개의 B 요소를 공유 메모리에 적재해야한다는 것을 의미합니다. 따라서, 각 블록은 A와 B 배열 요소를 공유 메모리에 적재하기 위해서 (1024 + 1024)*4 = 8192바이트의 공유 메모리를 전용으로 사용하게 됩니다.
간단한 예시로 33,000개의 요소(m=33,000)로 구성된 배열 A와 31,000개의 요소(n=31,000)로 구성된 배열 B를 병합한다고 가정해봅시다. 출력 배열 C 요소의 총 개수는 64,000개가 됩니다. 각 블록에서 16개의 블록(gridDim.x=16)과 128개의 스레드(blockDim.x=128)을 사용한다고 가정하면, 각 블록은 64,000/16 = 4,000개의 출력 배열의 subarray를 생성하게 됩니다. 그리고 tile_size가 1024이기 때문에, 커널의 while 루프는 4000개의 출력 배열 요소를 채우기 위해서 각 블록에서 각각 4번씩 반복될 것입니다.
커널 함수의 두 번째 파트와 세 번째 파트는 while 루프에서 반복적으로 수행됩니다.
int counter = 0; int C_length = C_next - C_curr; int A_length = A_next - A_curr; int B_length = B_next - B_curr; int total_iteration = ceil((C_length)/(float)tile_size); int C_completed = 0; int A_consumed = 0; int B_consumed = 0; while (counter < total_iteration) { /* Part 2 : Loading A and B elements into the shared memory */ // loading tile-size A and B elements into shared memory for (int i = 0; i < tile_size; i += blockDim.x) { if (i + threadIdx.x < A_length - A_consumed) A_S[i + threadIdx.x] = A[A_curr + A_consumed + i + threadIdx.x]; } for (int i = 0; i < tile_size; i += blockDim.x) { if (i + threadIdx.x < B_length - B_consumed) B_S[i + threadIdx.x] = B[B_curr + B_consumed + i + threadIdx.x]; } __syncthreads();
두 번째 부분은 A와 B의 subarray 요소를 공유 메모리로 적재하는 역할을 담당하는데, 각 루프에서 A의 1024개의 요소와 B의 1024개의 요소를 각 블록의 모든 스레드들이 협력하여 로드합니다. 블록에 128개의 스레드가 있다면, 각 for문 반복에서 128개의 요소를 일괄적으로 로드할 수 있습니다. 따라서 위 코드의 첫 번째 for문는 블록에 있는 모든 스레드에 대해서 8번 반복하여 1024개의 A 요소를 공유 메모리로 로드합니다. 두 번째 for문도 8번 반복하여 1024개의 B 요소를 공유 메모리로 로드합니다. 스레드는 threadIdx.x의 값을 사용하여 로드할 요소를 선택하므로 연속된 스레드는 연속된 메모리에 위치한 요소를 로드합니다. 따라서, 메모리 액세스가 하나로 병합되어 수행됩니다.
(for문에 있는 if 조건문은 조금 뒤에서 살펴보겠습니다.)
공유 메모리에 적재가 완료되면, 세 번째 파트로 넘어갑니다. 두 번째 파트에서 입력 subarray의 타일이 공유 메모리에 위치하면, 각각의 스레드가 입력의 타일을 분할하여 병렬로 merge할 수 있습니다. 이는 각 스레드에 출력 배열의 구역을 할당하고, co-rank 함수를 호출하여 각 스레드의 출력 배열 구역을 생성하는데 필요한 공유 메모리 데이터의 범위를 결정합니다. 이 단계는 아래의 코드에서 수행됩니다. (두 번째 파트에 이어지는 while루프의 본문입니다.)
/* Part 3 : All threads merge their individual subarrays in parallel */ int c_curr = threadIdx.x * (tile_size/blockDim.x); int c_next = (threadIdx.x+1) * (tile_size/blockDim.x); c_curr = (c_curr <= C_length - C_completed) ? c_curr : C_length - C_completed; c_next = (c_next <= C_length - C_completed) ? c_next : C_length - C_completed; // find co-rank for c_curr and c_next int a_curr = co_rank(c_curr, A_S, min(tile_size, A_length-A_consumed), B_S, min(tile_size, B_length-B_consumed)); int b_curr = c_curr - a_curr; int a_next = co_rank(c_next, A_S, min(tile_size, A_length-A_consumed), B_S, min(tile_size, B_length-B_consumed)); int b_next = c_next - a_next; // All threads call the sequential merge function sequentialMerge(A_S + a_curr, a_next - a_curr, B_S + b_curr, b_next - b_curr, C + C_curr + C_completed + c_curr); // Update the A and B elements that have been consumed thus far counter++; C_completed += tile_size; A_consumed += co_rank(tile_size, A_S, tile_size, B_S, tile_size); B_consumed = C_completed - A_consumed; __syncthreads(); }
각 while 반복동안 블록의 스레드는 공유 메모리에 로드한 데이터를 사용하여 tile_size만큼의 C 요소를 생성합니다. 마지막 반복에서 예외가 존재하는데, 이는 조금 뒤에서 다루도록 하겠습니다.
co_rank 함수는 각 스레드에 의해서 수행되는데, 먼저 현재 스레드에서의 출력 배열의 범위의 시작 인덱스(c_curr)와 다음 스레드의 시작 위치(c_next)를 계산하고, 입력의 범위를 계산하기 위해서 c_curr과 c_next를 co_rank 함수의 인자로 전달합니다.
위에서 사용한 동일한 예제로 살펴보겠습니다. 각 while 루프의 반복에서 블록의 모든 스레드는 공유 메모리에 적재된 A와 B 요소의 입력 타일을 사용하여 1024개의 출력 요소를 생성합니다. 이 작업은 128개의 스레드에 의해서 수행되므로, 각 스레드는 8개의 출력 요소를 생성하게 됩니다. 각 스레드가 공유 메모리에서 총 8개의 입력 요소를 사용한다는 것을 알고 있지만, 우리는 각 스레드가 사용하는 A 요소와 B 요소의 정확한 개수를 알기 위해서 co-rank 함수를 호출할 필요가 있습니다(line 20). 일부 스레드는 3개의 A 요소와 5개의 B 요소를 사용할 수도 있고, 다른 스레드는 6개의 A 요소와 2개의 B 요소를 사용할 수도 있기 때문입니다.
우리의 예제에서 한 번에 반복에서 블록의 모든 스레드들에 의해서 사용되는 A와 B 요소의 총 개수는 1024개가 될 것입니다. 만약 블록 내의 모든 스레드에서 476개의 A 요소가 사용되었다면, B 요소는 1024-476=548개를 사용했음을 알 수 있습니다. 모든 스레드가 1024개의 A 요소만을 사용하는 극단적인 상황(B 요소는 사용하지 않음)이 발생할 수도 있습니다. 총 2048개의 요소가 공유 메모리에 로드되는데, 각 while루프 반복에서 공유 메모리에 로드된 A와 B 요소의 절반만의 블록의 모든 스레드에 의해서 사용됩니다. 그리고 Merge Operation은 sequential merge함수를 호출하여 A와 B 요소의 일부를 사용하여 지정된 범위의 C 요소를 생성합니다.
커널 함수의 변수에 대한 자세한 내용은 아래 접기를 펼쳐서 확인해주세요 !
while 루프의 각 반복에서 A와 B 배열의 현재 타일을 로드하는 시작 위치는 while 루프의 이전 반복동안 블록의 모든 스레드에 의해서 사용된 A와 B 요소의 개수에 따라서 달라집니다.
이전 반복에서 사용된 A 요소의 총 개수를 추적하기 위해서 변수 A_consumed를 사용하고, 이 값은 처음에는 0으로 초기화됩니다. 첫 번째 반복의 시작 부분에서 A_consumed의 값은 0이기 때문에 모든 블록들은 A[A_curr]부터 입력 타일을 시작합니다. 이어지는 반복에서 A 요소의 타일은 A[A_curr + A_consumed]부터 시작됩니다.
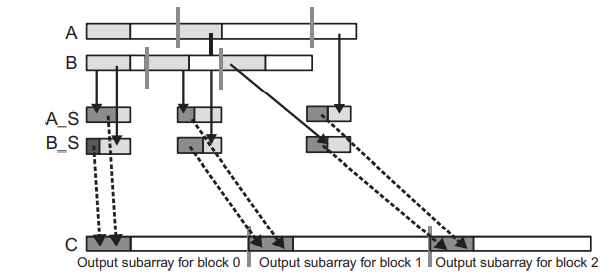
위 그림은 첫 번째 반복(Iteration 0)에서 각 스레드에 의해서 사용되는 A_S 요소(짙은 회색)를 보여주고, 아래 그림은 두 번째 반복(Iteration 1)에서의 인덱스 계산을 보여줍니다.
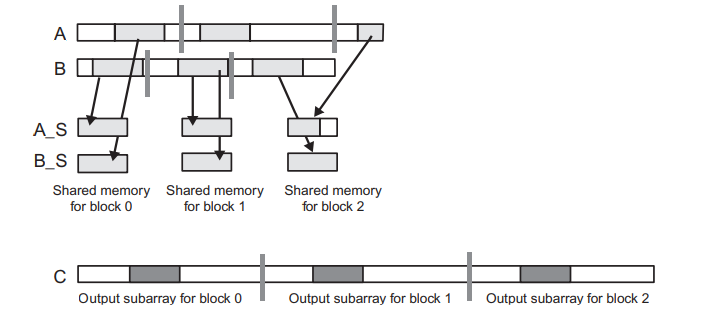
두 번째 반복에서 블록 0이 전역 메모리에서 로드할 타일은 첫 번째 반복에서 사용된 A 요소를 포함하는 섹션 바로 다음 위치에서 시작해야 합니다. 사용된 A 요소를 포함하는 섹션은 위 그림 위쪽의 A 배열에서 각 블록에 할당된 subarray의 시작 부분에 위치한 흰색 부분입니다. 이 부분의 길이는 A_consumed 값으로 주어지기 때문에 두 번째 루프에서 로드될 타일은 A[A_curr + A_consumed]부터 시작합니다. 마찬가지로, B 배열에서 로드될 타일은 B[B_curr + B_conumsed]부터 시작합니다.
이렇게 이전 반복에서 블록에 의해 사용된 A와 B 요소의 총 개수를 A_consumed, B_consumed 변수를 통해 제공하므로, 타일을 로드하는 프로세스는 잘 동작합니다. 사용된 요소의 수를 업데이트하는 코드는 커널 함수 세 번째 파트의 마지막 부분(while 루프의 끝 부분)에 있습니다.
마지막 반복을 제외한 모든 반복에서는 tile_size 만큼의 C 요소를 생성하게 됩니다. (C_completed += tile_size;)
그리고 이어지는 문장들은 블록의 스레드에서 사용된 A 및 B 요소의 총 수를 업데이트합니다. 마지막 반복을 제외한 모든 경우에 블록에서 사용된 A 요소의 수는 co_rank 함수에 의해서 반환된 값입니다.
A_consumed += co_rank(tile_size, A_S, tile_size, B_S, tile_size);앞에서 언급했지만, 사용되는 요소의 수의 계산은 while 루프의 마지막 반복에서는 정확하지 않을 수 있습니다. 이는 마지막 반복에서 tile_size 만큼의 요소가 남아있지 않을 수 있기 때문입니다. 따라서, 마지막 반복에서는 tile_size만큼의 요소를 생성하는 것이 아닌 A_length, B_length, C_length 값을 사용하여 계산해야 합니다. 이러한 이유 때문에 while 루프 내에서 if 조건문과 3항연산자, min을 사용하고 있습니다.
기존 코드에 Tile Merge Operation을 추가하여, 각 함수의 성능을 비교해봤습니다.
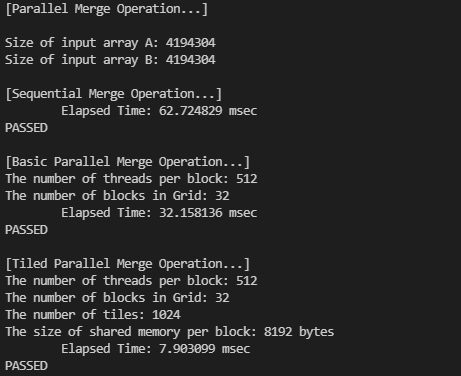
Tiled Merge Operation 커널은 Baisc Merge Operation 커널보다 약 4~5배 빠른 속도로 수행되는 것을 확인할 수 있습니다. 전체 코드는 마찬가지로 아래 링크에서 확인하실 수 있습니다.
https://github.com/junstar92/parallel_programming_study/blob/master/CUDA/mergeSort/mergeOperation.cu
GitHub - junstar92/parallel_programming_study: Study parallel programming - CUDA, OpenMP, MPI, Pthread
Study parallel programming - CUDA, OpenMP, MPI, Pthread - GitHub - junstar92/parallel_programming_study: Study parallel programming - CUDA, OpenMP, MPI, Pthread
github.com
타일링을 적용한 커널은 co-rank 함수에 의한 전역 메모리 액세스를 상당히 감소시켜주고, 전역 메모리 액세스를 병합시켜줍니다. 하지만, 이 커널은 심각한 결함이 있는데, 커널 함수에서 공유 메모리에 적재된 데이터의 절반만을 사용합니다. 공유 메모리에서 사용되지 않은 데이터는 다음 반복 시에 다시 로드되는데, 이로 인해서 메모리 대역폭의 절반이 낭비됩니다.
A Circular-Buffer Merge Kernel
circular buffer scheme를 사용하면 공유 메모리에 로드된 A와 B의 모든 요소를 커널이 완전히 활용할 수 있습니다.
공유 메모리를 circular queue처럼 circular buffer로 사용하는 것인데, ring buffer라고도 합니다.
이를 사용한 circular-buffer merge kernel은 merge_tiled_kernel 함수와 크게 비슷합니다. 다만, circular buffer를 사용하기 때문에 기존에 사용한 A와 B의 인덱스를 사용할 수 없으므로, circular buffer를 사용하는 sequential merge 함수와 co-rank 함수를 새롭게 정의해주어야 합니다.
두 함수는 아래와 같이 구현할 수 있습니다.
__host__ __device__ int co_rank_circular(int k, int* A, int m, int* B, int n, int A_S_start, int B_S_start, int tile_size) { int i = (k < m) ? k : m; // i = min(k, m); int j = k-i; int i_low = (0 > (k-n)) ? 0 : k-n; // i_low = max(0, k-n); int j_low = (0 > (k-m)) ? 0 : k-m; // j_low = max(0, k-m); int delta; bool active = true; while (active) { int i_cir = (A_S_start + i >= tile_size) ? A_S_start + i - tile_size : A_S_start + i; int i_m_1_cir = (A_S_start + i - 1 >= tile_size) ? A_S_start + i - 1 - tile_size : A_S_start + i - 1; int j_cir = (B_S_start + j >= tile_size) ? B_S_start + j - tile_size : B_S_start + j; int j_m_1_cir = (B_S_start + j - 1 >= tile_size) ? B_S_start + j - 1 - tile_size : B_S_start + j - 1; if (i > 0 && j < n && A[i_m_1_cir] > B[j_cir]) { delta = ((i - i_low + 1) >> 1); j_low = j; j = j + delta; i = i - delta; } else if (j > 0 && i < m && B[j_m_1_cir] >= A[i_cir]) { delta = ((j - j_low + 1) >> 1); i_low = i; i = i + delta; j = j - delta; } else { active = false; } } return i; } __host__ __device__ void sequentialMergeCircular(int* A, int m, int* B, int n, int* C, int A_S_start, int B_S_start, int tile_size) { int iA = 0, iB = 0, iC = 0; while ((iA < m) && (iB < n)) { int iA_cir = (A_S_start + iA >= tile_size) ? A_S_start + iA - tile_size : A_S_start + iA; int iB_cir = (B_S_start + iB >= tile_size) ? B_S_start + iB - tile_size : B_S_start + iB; if (A[iA_cir] <= B[iB_cir]) { C[iC++] = A[iA_cir]; iA++; } else { C[iC++] = B[iB_cir]; iB++; } } if (iA == m) { while (iB < n) { int iB_cir = (B_S_start + iB >= tile_size) ? B_S_start + iB - tile_size : B_S_start + iB; C[iC++] = B[iB_cir]; iB++; } } else { while (iA < m) { int iA_cir = (A_S_start + iA >= tile_size) ? A_S_start + iA - tile_size : A_S_start + iA; C[iC++] = A[iA_cir]; iA++; } } }
그리고 circular buffer를 사용한 merge 커널 함수는 다음과 같이 구현할 수 있습니다. 각 블록에서 처리되는 A와 B의 subarray의 요소들을 공유 메모리 A_S와 B_S에 로드하는데, 각 반복에서 새롭게 tile_size만큼의 요소를 로드하는 것이 아니라, 이전 반복에서 사용한 만큼을 다시 채워넣는 방식으로 로드합니다. 이렇게 함으로써 각 반복에서 사용하지 않은 요소들은 다음 반복에서 사용되도록 재활용됩니다. 다만, 각 스레드에서 사용되는 레지스터의 수가 증가한다는 단점이 있습니다.
__global__ void merge_circular_buffer_kernel(int* A, int m, int* B, int n, int* C, int tile_size) { /* Part 1 : Identifying block-level output and input subarrays */ extern __shared__ int shareAB[]; int* A_S = shareAB; int* B_S = shareAB + tile_size; int C_curr = blockIdx.x * ceil((m+n)/(float)gridDim.x); int C_next = min((blockIdx.x+1) * (int)ceil((m+n)/(float)gridDim.x), m+n); if (threadIdx.x == 0) { A_S[0] = co_rank(C_curr, A, m, B, n); A_S[1] = co_rank(C_next, A, m, B, n); } __syncthreads(); int A_curr = A_S[0]; int A_next = A_S[1]; int B_curr = C_curr - A_curr; int B_next = C_next - A_next; __syncthreads(); int counter = 0; int C_length = C_next - C_curr; int A_length = A_next - A_curr; int B_length = B_next - B_curr; int total_iteration = ceil((C_length)/(float)tile_size); int C_completed = 0; int A_consumed = 0; int B_consumed = 0; int A_S_start = 0; int B_S_start = 0; int A_S_consumed = tile_size; // in the first iteration, fill the tile_size int B_S_consumed = tile_size; // in the first iteration, fill the tile_size while (counter < total_iteration) { /* Part 2 : Loading A and B elements into the shared memory */ // loading A_S_consumed elements into A_S for (int i = 0; i < A_S_consumed; i += blockDim.x) { if (i + threadIdx.x < A_length - A_consumed && i + threadIdx.x < A_S_consumed) A_S[(A_S_start + i + threadIdx.x) % tile_size] = A[A_curr + A_consumed + i + threadIdx.x]; } // loading B_S_consumed elements into B_S for (int i = 0; i < B_S_consumed; i += blockDim.x) { if (i + threadIdx.x < B_length - B_consumed && i + threadIdx.x < B_S_consumed) B_S[(B_S_start + i + threadIdx.x) % tile_size] = B[B_curr + B_consumed + i + threadIdx.x]; } __syncthreads(); /* Part 3 : All threads merge their individual subarrays in parallel */ int c_curr = threadIdx.x * (tile_size/blockDim.x); int c_next = (threadIdx.x+1) * (tile_size/blockDim.x); c_curr = (c_curr <= C_length - C_completed) ? c_curr : C_length - C_completed; c_next = (c_next <= C_length - C_completed) ? c_next : C_length - C_completed; // find co-rank for c_curr and c_next int a_curr = co_rank_circular(c_curr, A_S, min(tile_size, A_length-A_consumed), B_S, min(tile_size, B_length-B_consumed), A_S_start, B_S_start, tile_size); int b_curr = c_curr - a_curr; int a_next = co_rank_circular(c_next, A_S, min(tile_size, A_length-A_consumed), B_S, min(tile_size, B_length-B_consumed), A_S_start, B_S_start, tile_size); int b_next = c_next - a_next; // All threads call the circular-buffer version of sequential merge function sequentialMergeCircular(A_S, a_next - a_curr, B_S, b_next - b_curr, C + C_curr + C_completed + c_curr, A_S_start + a_curr, B_S_start + b_curr, tile_size); // Update the A and B elements that have been consumed thus far counter++; A_S_consumed = co_rank_circular(min(tile_size, C_length-C_completed), A_S, min(tile_size, A_length-A_consumed), B_S, min(tile_size, B_length-B_consumed), A_S_start, B_S_start, tile_size); B_S_consumed = min(tile_size, C_length-C_completed) - A_S_consumed; A_consumed += A_S_consumed; C_completed += min(tile_size, C_length-C_completed); B_consumed = C_completed - A_consumed; A_S_start = A_S_start + A_S_consumed; if (A_S_start >= tile_size) A_S_start = A_S_start - tile_size; B_S_start = B_S_start + B_S_consumed; if (B_S_start >= tile_size) B_S_start = B_S_start - tile_size; __syncthreads(); } }
이전과 동일한 조건으로 circular-buffer merge kernel을 실행해봤습니다....
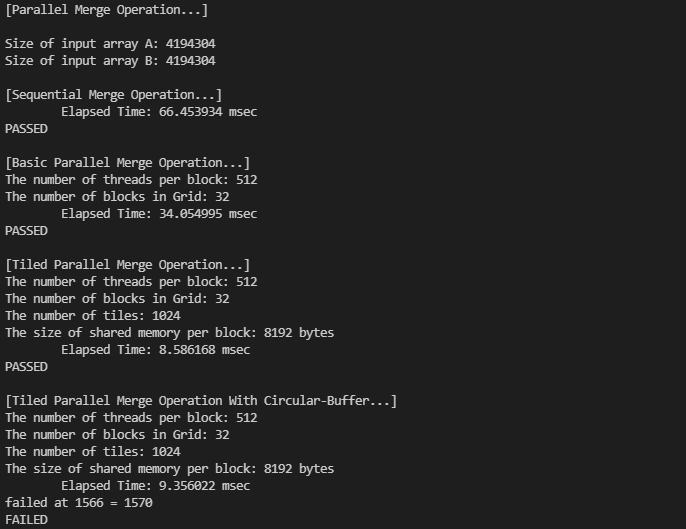
보다시피... 무언가 잘못된 것 같은데, 사실 아직 어떤 부분에 에러가 있는지 발견하지는 못했습니다.
다만, tile의 크기를 8192까지 증가시켜주면, 병합 연산이 정상적으로 수행되는 것을 확인했습니다. tiled merge kernel과 circular-buffer merge kernel의 수행 시간은 큰 차이가 없었습니다.
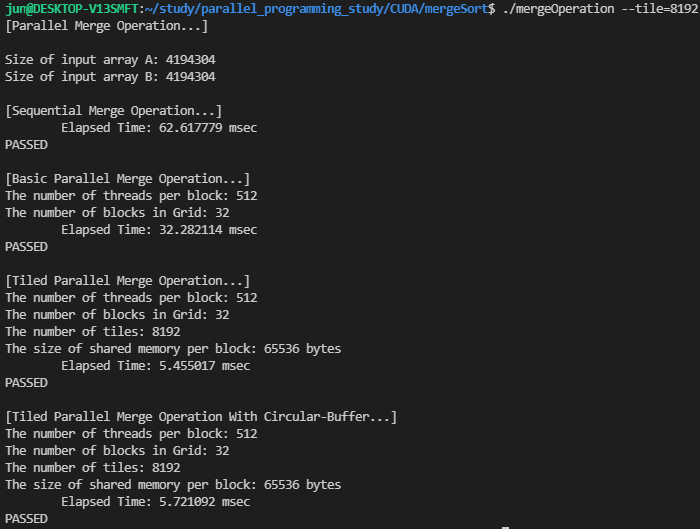
엣지 케이스와 같은 문제점이 있는 것 같은데.. 아직 원인은 발견하지 못했습니다... 이러한 문제점은 circular merge가 아닌 tiled merge 커널에서도 발생하는 것 같습니다.. !
완벽한 커널 함수를 구현하고 싶었으나, 아직 많이 부족한 관계로 일단 책에 제공해주는 커널 함수를 사용했습니다만 기회가 된다면 완전한 Merge Sort를 구현해보도록 하겠습니다!
(책의 커널 함수는 정렬된 배열 A와 B를 입력으로 사용하고 있습니다.)
'NVIDIA > CUDA' 카테고리의 다른 글
| CUDA Dynamic Parallelism (동적 병렬) (2) | 2022.01.01 |
|---|---|
| Graph Search (Breadth-First Search) (0) | 2021.12.30 |
| Sparse Matrix Computation (0) | 2021.12.21 |
| Parallel Histogram (0) | 2021.12.18 |
| Parallel Prefix Sum (2) (0) | 2021.12.17 |




댓글