References
- Programming Massively Parallel Processors
Contents
- Breadth-First Search (BFS)
- A Sequential BFS Function
- A Parallel BFS Function
- Optimization
이번에 살펴 볼 병렬 패턴은 Graph Search입니다. 그래프는 개체(entity)간의 관계(relation)를 나타내는 자료구조이며, 이 개체(entity)는 vertices(정점)으로 표현하고 관계는 edges(간선)으로 표현합니다. 세상의 많은 중요한 문제들은 아주 큰 스케일의 그래프 문제로 볼 수 있습니다. 예를 들면, 소셜 네트워크나 네비게이션 등이 있습니다.
그래프는 알고보면 희소 행렬(sparse matrix)와도 관련이 있습니다. 실제로 그래프 연산은 희소 행렬 연산으로 공식화될 수 있습니다.
이번 포스팅에서는 실제 많은 어플리케이션의 기반이 되는 그래프 연산(graph computation)인 그래프 검색(graph search)에 초점을 맞추어서 알아보겠습니다. 그래프 검색 연산은 사실 정점의 값을 조사하는 것이기 때문에, 한번 메모리로부터 로드된 정점값에 대한 계산은 거의 없습니다. 따라서, 그래프 검색의 속도는 일반적으로 메모리 대역폭(memory bandwidth)에 달려있습니다.
+) 아래에서 BFS를 수행하기 전에 그래프 데이터를 CSR(Compressed Sparse Row) Format으로 변환하여 수행합니다. CSR Format에 대해서는 아래 포스팅을 참조하시기 바랍니다 !
Sparse Matrix Computation
References Programming Massively Parallel Processors Contents Sparse Matrix, CSR Parallel SpMV Using CSR ELL Format Hybrid Approach to Regulate Padding 본문에 사용된 코드는 아래 링크에서 확인하실 수..
junstar92.tistory.com
Background
이미 그래프 자료구조에 대해서는 잘 아시리라 생각이 되지만, 복습 겸 책에서 설명하는 그래프에 대해서 알아보겠습니다.
처음 언급했듯이, 그래프는 개체들 간의 관계를 나타내는 자료구조입니다. 예를 들어, 소셜 미디어에서 각 entity는 유저가 되고, 관계(relations)는 유저들간의 커넥션이 됩니다. 다른 예로, 네비게이션 시스템에서 entities는 장소(location)이고, 관계는 장소들 간의 도로를 의미하게 됩니다. 어떤 관계는 소셜 네트워크의 친구 관계처럼 양방향(bi-directional)일 수 있지만(방향성이 없는 간선edges), 어떤 관계는 일방통행 도로처럼 단방향일 수 있습니다(간선의 방향이 존재).
오늘 포스팅에서는 방향 그래프(Directed Graph)에 대해 초점을 맞추어 보겠습니다. 그래프에서 방향이 있는 간선은 source vertex에서 destination vertex로 화살표 모양의 간선으로 나타냅니다.
아래 그림은 간단한 방향 그래프를 보여줍니다.

각각의 정점에는 번호가 할당되어 있고, 0에서 1로 나가는 간선, 0에서 2로 나가는 간선 등이 있습니다. 이를 장소와 도로라고 생각하고 0에서 5로 갈 수 있는 루트를 찾는다면, 가능한 길은 아래와 같이 총 3개가 있을 수 있습니다.
0->1->3->4->5 / 0->1->4->5 / 0->2->5
그래프는 직관적이 표현으로 인접 행렬(adjacency matrix)을 통해 표현할 수 있습니다. 각 정점에 0부터 시작하는 번호를 부여했고, 정점 i에서 정점 j로의 간선이 있을 때, 인접 행렬의 원소 A[i][j]의 값은 1이 되고, 간선이 없다면 0이 됩니다.
아래 그림은 위의 그래프를 인접 행렬로 나타낸 것을 보여줍니다.

그래프에서 우리는 정점 1에서 3으로의 간선이 존재하기 때문에 A[1][3]의 값이 1이라는 것을 확인할 수 있습니다. 비어이는 값은 이어지는 간선이 없다는 의미이고, 이 값들은 모두 0입니다.
만약 N개의 정점이 있는 그래프가 완전히 연결(fully connected)되어 있다면, 각 정점에서 나가는 간선은 (N-1)개가 됩니다. 자기 자신으로 향하는 간선은 없기 때문에 한 정점에서 나가는 간선의 수는 (N-1)개입니다. 예를 들어, 위에서 본 9개의 정점을 가지는 그래프가 완전히 연결되어 있다면, 각 정점에서 나가는 간선은 8개가 되고, 그래프 전체에는 총 72개의 간선이 있습니다.
위에서 본 간단한 그래프는 많이 연결되어 있지 않습니다. 각 간선은 0~3개의 나가는 간선을 갖고 있습니다.
이러한 그래프를 sparsely connected 라고 말합니다. 즉, 각 정점으로부터 나가는 간선의 평균 개수가 N-1보다 한참 적습니다.
이러한 점 때문에, sparsely connected graph는 sparse matrix representation으로 변환하여 더 효율적으로 활용할 수 있습니다. 실제로, 세상에 존재하는 그래프들은 드문드문 연결되어 있습니다. 페이스북, 트위터, 링크드인과 같은 소셜 네트워크에서 각 유저의 평균적인 커넥션은 전체 유저의 수보다 한참 적습니다. 따라서, 인접 행렬에서 0이 아닌 요소의 수가 전체 요소의 수보다 한참 적습니다.
그래서 CSR과 같은 형식을 사용하면 0인 요소에 낭비되는 연산과 총 저장 공간을 감소시킬 수 있습니다.
아래 그림은 위의 그래프 예제를 CSR 형식으로 나타낸 것입니다.
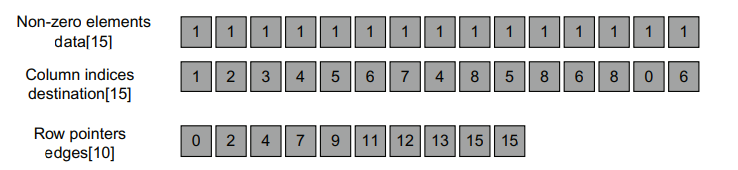
row pointer array는 edges array로 사용합니다. 간단히 설명하면, 각 row pointer는 각 row에서 0이 아닌 요소의 시작 위치를 알려줍니다. 예를 들어, edges[3] = 7은 row 3에서 0이 아닌 요소의 시작 지점을 알려주고 edges[4] = 9는 row 4의 0이 아닌 요소의 시작 지점을 알려줍니다. 이를 통해 우리는 row 3의 0이 아닌 data가 data[7]과 data[8]에 있고, 이 data의 column 인덱스가 destination[7]과 destination[8]의 값이라는 것을 알 수 있습니다.
사실 data array는 불필요합니다. data의 모든 요소의 값이 1이기 때문에 실제로는 저장할 필요가 없습니다.
사실 1이 아닌 다른 값 또는 자료형을 사용할 수 있는데, 이때 값은 두 위치 사이의 거리 또는 두 셔설 네트워크 사용자가 커넥션된 날짜와 같은 추가 정보가 될 수 있습니다. 이러한 경우에는 data array를 사용해야 합니다.
Sparse representation은 인접 행렬을 저장하는데 상당한 공간을 절약할 수 있습니다. 위의 예제에서 만약 data array를 제거한다면, CSR 표현으로 변환하여 81개의 공간에서 25개의 공간으로 56개의 공간을 절약할 수 있게 됩니다. 실제로 0이 아닌 요소의 비율은 굉장히 적기 때문에 절약할 수 있는 공간은 엄청날 수 있습니다.
Breadth-First Search (BFS)
Breadth-First Search(BFS, 너비우선탐색)는 중요한 그래프 연산 중의 하나입니다. BFS는 보통 한 정점에서 다른 정점까지 가는데 필요한 가장 작은 수의 간선을 찾는데 사용됩니다. BFS의 형태는 다양하고, 각 방법은 다른 유형의 결과를 도출하지만 일반적으로 한 유형의 결과를 다른 유형의 결과로부터 도출할 수 있습니다.
가장 간단한 형태의 BFS는 source인 정점에서 해당 정점으로 이동하기 위해 필요한 가장 작은 간선의 수를 라벨링하는 것입니다.
아래 이미지의 (A)는 정점 0을 source로 사용한 BFS 결과를 보여줍니다. 정점 0에서 하나의 간선을 통해 정점 1, 2에 도달할 수 있습니다. 따라서, 각 정점(1, 2)에는 level 1이라고 표시합니다. 그리고 다른 간선들을 탐색하면서 정점 1로부터 정점 3, 4에 도달하고, 정점 2로부터 정점 5, 6, 7에 도달합니다. 그리고 이 정점들(3,4,5,6,7)에 level 2라고 표시합니다. 마지막으로 하나의 간선을 더 탐색하여 정점 8(level 3)에 도달합니다.
보면 알겠지만, 다른 정점을 source로 지정하면 BFS 결과는 달라집니다.
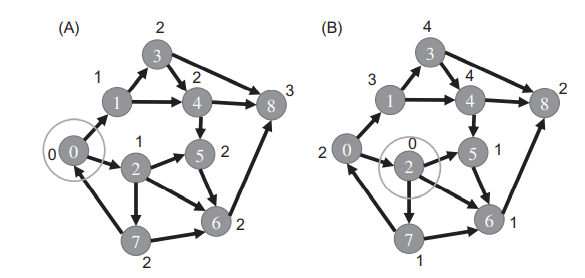
위 그림의 (B)는 정점 2를 source로 지정하고, BFS를 수행했습니다. level 1의 정점은 5, 6, 7이며, level 2의 정점은 8, 0 입니다. 정점 1만이 level 3이고, 마지막으로 정점 3, 4는 level 4입니다. 하나의 간선만큼 떨어진 정점으로 source를 옮겼는데, 그 결과는 상당히 다릅니다.
이렇게 모든 정점에 라벨링을 하고나면, source로 부터 다른 정점까지의 경로에 이동해야하는 간선의 수를 쉽게 찾을 수 있습니다. 예를 들어, 위 그림의 (B)에서 정점 1은 level 3으로 표시되어 있는데, 이를 통해 source(정점 2)에서 1로 가는데 필요한 가장 적은 간선의 수가 3이라는 것을 알 수 있습니다.
만약 경로를 찾기 원한다면, 도착 정점으로부터 거꾸로 시작 정점까지 찾아나가면 됩니다. 여기서 같은 level의 이전 정점이 여러개가 있다면 아무거나 고르면 됩니다. 이렇게 선택할 수 있는 것이 많다는 것은 결과가 동일한 방법이 여러 개 있다는 것을 의미합니다.
A Sequential BFS Function
순차 BFS 함수를 먼저 살펴보겠습니다. 그래프는 아래와 같은 CSR 포맷으로 변환하여 사용한다고 가정합니다.

BFS 함수는 source 정점의 인덱스와 그래프의 edges array(edges), destination array(dest)를 파라미터로 전달받습니다. 그리고 label array 또한 전달받는데, 이는 각 정점에 방문 상태 정보를 저장하는데 사용됩니다.
탐색을 시작하기 전에, source의 label 요소는 level 0을 의미하는 값인 0으로 초기화됩니다. 그리고 나머지 모든 label 요소들은 -1로 초기화합니다. 이는 연관된 정점에 아직 방문하지 않았다는 것을 의미합니다. 탐색이 끝나면, source로부터 도달할 수 있는 정점들에 대응하는 모든 label 배열의 요소들은 positive level 값을 가지게 됩니다. 만약 여전이 그 값이 -1이라면 해당 정점은 source로부터 도달할 수 없다는 것을 의미합니다.
sequential BFS 함수는 다음과 같습니다.
void BFS_sequential(int source, int* edges, int* dest, int* label)
{
int frontier[2][MAX_FRONTIER_SIZE];
int *c_frontier = frontier[0];
int c_frontier_tail = 0;
int *p_frontier = frontier[1];
int p_frontier_tail = 0;
insert_frontier(source, p_frontier, &p_frontier_tail);
label[source] = 0;
while (p_frontier_tail > 0) {
for (int f = 0; f < p_frontier_tail; f++) {
int c_vertex = p_frontier[f];
for (int i = edges[c_vertex]; i < edges[c_vertex+1]; i++) {
if (label[dest[i]] == -1) {
insert_frontier(dest[i], c_frontier, &c_frontier_tail);
label[dest[i]] = label[c_vertex] + 1;
}
}
}
int *tmp = c_frontier;
c_frontier = p_frontier;
p_frontier = tmp;
p_frontier_tail = c_frontier_tail;
c_frontier_tail = 0;
}
}코드가 익숙하지 않겠지만, Queue를 배열로 사용하고 있다고 이해하시면 조금 더 쉽게 코드를 이해할 수 있을 것 같습니다.
이 함수에서는 두 개의 frontier array를 사용합니다. 하나는 이전 반복에서 방문한 정점들을 저장하고 있고, 다른 하나는 현재 반복에서 방문한 정점들을 저장합니다. 이 배열은 frontier[0][MAX_FRONTIER_SIZE]와 frontier[1][MAX_FRONTIER_SIZE]로 선언되어 있습니다. 두 배열의 역할은 반복할 때마다 서로 바뀝니다.
이렇게 역할을 바꿈으로써 다음 반복을 진행하기 전에 현재 frontier 배열의 값들을 이전 frontier 배열로 복사해야하는 작업을 피할 수 있게 해줍니다. 이러한 기법을 ping-pong buffer라고 부릅니다.
각 정점으로부터 나가는 정점의 최대 개수가 N-1개이기 때문에, 위의 9개 정점이 있는 그래프 예제에서 MAX_FRONTIER_SIZE의 크기를 9로 지정하였습니다.
이 함수는 label 배열의 모든 요소들의 값이 -1로 초기화되어 있다고 가정합니다. 함수의 시작 부분에서 label[source]의 값은 0으로 초기화되고, 이는 탐색에서 source가 level 0 정점이라는 것을 의미합니다.
그리고 포인터 변수인 c_frontier는 현재(current) frontier 배열의 시작을 가리키고, 다른 포인터 변수인 p_frontier는 이전(preivous) frontier 배열의 시작을 가리킵니다. 함수의 시작 부분에서 c_frontier는 frontier[0]을 가리키는 포인터로 초기화되고, p_frontier는 frontier[1]을 가리키는 포인터로 초기화됩니다.
또한, 두 개의 tail 인덱스를 사용하는데, p_frontier_tail 변수는 previous frontier에 삽입된 정점의 개수를 가리키고, c_frontier_tail 변수는 current frontier에 삽입되는 정점들의 수가 저장됩니다.
while 루프는 이전 반복에서 방문한 정점들을 저장하고 있는 p_frontier의 크기가 0이 될 때까지 반복합니다. 루프 내의 코드는 매우 간단하며, 이전 반복에서 방문한 정점들을 순회하면서 각 정점으로부터 나가는 간선을 통해 방문할 수 있는 정점들을 탐색하여, 이전에 방문하지 않은 정점이었다면 label 값을 업데이트하고 c_frontier에 방문한 정점을 삽입합니다. 순회가 끝나면, p_frontier와 c_frontier의 포인터를 스왑하고 다시 루프를 반복합니다.
(git 코드에 STL의 queue를 사용하여 구현한 BFS 함수가 있습니다. 이를 참조하시면 더욱 쉽게 이해하실 것 같습니다.)
위에서 살펴본 그래프 예제를 입력으로 사용하여 위 순차 BFS 함수를 실행하면 다음의 결과를 얻을 수 있습니다.

각 정점에서의 label 값은 0, 1, 1, 2, 2, 2, 2, 2, 3으로, 위에서 살펴본 결과와 동일합니다.
전체 코드는 아래 링크를 통해 확인하실 수 있습니다.
https://github.com/junstar92/parallel_programming_study/blob/master/CUDA/BFS/bfs.cu
GitHub - junstar92/parallel_programming_study: Study parallel programming - CUDA, OpenMP, MPI, Pthread
Study parallel programming - CUDA, OpenMP, MPI, Pthread - GitHub - junstar92/parallel_programming_study: Study parallel programming - CUDA, OpenMP, MPI, Pthread
github.com
A Parallel BFS Function
BFS를 병렬화할 때에는 몇 가지 방법들이 존재합니다.
예를 들어, Harish와 Narayanan은 각 스레드에 하나의 정점을 할당한 병렬화를 제안했습니다. 각 반복동안, 모든 정점을 방문합니다. 만약 할당된 정점이 이전 반복에서 소스로부터 나오는 간선에 의해 방문했다면, 그 정점은 현재 반복에서 방문한 것으로 표시됩니다. 여기서 작업량은 V*L에 비례하는데, V는 그래프에서 정점의 총 개수이고, L은 검색 결과에서 level의 수입니다. 만약 그래프가 매우 크다면, level의 수는 상당히 많을 것이고 알고리즘의 효율은 매우 낮아져서 순차 코드보다 더 느리게 실행될 수 있습니다.
순차 알고리즘과 비교할만한 효율을 가진 BFS 알고리즘을 설계할 수 있는데, Luo 등은 previous frontier 배열을 협업하여 처리하고 current frontier 배열을 모으기 위해 여러 스레드를 사용하여 위의 순차 코드의 while-loop를 병렬화하도록 제안했습니다. 우리는 이 방향으로 코드를 구현해보겠습니다.
이 병렬화 전략은 각 스레드 블록에 previous frontier 배열의 섹션을 할당하는 것입니다.
아래 코드는 커널 함수를 호출하기 위한 BFS Host 함수 입니다. 이 함수는 병렬로 각 반복을 수행하기 위한 간단한 흐름을 보여줍니다.

이를 함수로 구현하면 BFS_host는 다음과 같이 구현할 수 있습니다.
void BFS_host(int source, int* h_edges, int* h_dest, int* h_label, int numVertex, int numNonzero)
{
// host memory
int h_p_frontier_tail = 1;
// init
h_label[source] = 0;
// allocate device memory
int *d_edges, *d_dest, *d_label, *d_visited;
CUDA_CHECK(cudaMalloc((void**)&d_edges, (numVertex+1)*sizeof(int)));
CUDA_CHECK(cudaMalloc((void**)&d_dest, numNonzero*sizeof(int)));
CUDA_CHECK(cudaMalloc((void**)&d_label, numVertex*sizeof(int)));
CUDA_CHECK(cudaMalloc((void**)&d_visited, numVertex*sizeof(int)));
CUDA_CHECK(cudaMemcpy(d_edges, h_edges, (numVertex+1)*sizeof(int), cudaMemcpyHostToDevice));
CUDA_CHECK(cudaMemcpy(d_dest, h_dest, numNonzero*sizeof(int), cudaMemcpyHostToDevice));
CUDA_CHECK(cudaMemcpy(d_label, h_label, numVertex*sizeof(int), cudaMemcpyHostToDevice));
// allocate d_frontier, d_c_frontier_tail, d_p_frontier_tail
int *d_frontier, *d_c_frontier_tail, *d_p_frontier_tail;
CUDA_CHECK(cudaMalloc((void**)&d_frontier, 2*numNonzero*sizeof(int)));
CUDA_CHECK(cudaMalloc((void**)&d_c_frontier_tail, sizeof(int)));
CUDA_CHECK(cudaMalloc((void**)&d_p_frontier_tail, sizeof(int)));
int *d_c_frontier = &d_frontier[0];
int *d_p_frontier = &d_frontier[numVertex];
// init
CUDA_CHECK(cudaMemset(d_visited+source, 1, sizeof(int)));
CUDA_CHECK(cudaMemset(d_frontier+numVertex, source, sizeof(int)));
CUDA_CHECK(cudaMemcpy(d_p_frontier_tail, &h_p_frontier_tail, sizeof(int), cudaMemcpyHostToDevice));
CUDA_CHECK(cudaMemcpy(d_label, h_label, numVertex*sizeof(int), cudaMemcpyHostToDevice));
while (h_p_frontier_tail > 0) {
int num_blocks = (h_p_frontier_tail+BLOCK_SIZE-1) / BLOCK_SIZE;
BFS_Bqueue_kernel<<<num_blocks, BLOCK_SIZE>>>(d_p_frontier, d_p_frontier_tail, d_c_frontier, d_c_frontier_tail, d_edges, d_dest, d_label, d_visited);
CUDA_CHECK(cudaMemcpy(&h_p_frontier_tail, d_c_frontier_tail, sizeof(int), cudaMemcpyDeviceToHost));
int* temp = d_c_frontier;
d_c_frontier = d_p_frontier;
d_p_frontier = temp;
CUDA_CHECK(cudaMemcpy(d_p_frontier_tail, d_c_frontier_tail, sizeof(int), cudaMemcpyDeviceToDevice));
CUDA_CHECK(cudaMemset(d_c_frontier_tail, 0, sizeof(int)));
}
CUDA_CHECK(cudaMemcpy(h_label, d_label, numVertex*sizeof(int), cudaMemcpyDeviceToHost));
// free memory
CUDA_CHECK(cudaFree(d_edges));
CUDA_CHECK(cudaFree(d_dest));
CUDA_CHECK(cudaFree(d_label));
CUDA_CHECK(cudaFree(d_visited));
CUDA_CHECK(cudaFree(d_frontier));
CUDA_CHECK(cudaFree(d_c_frontier_tail));
CUDA_CHECK(cudaFree(d_p_frontier_tail));
}이 함수에서는 edges, dest, label을 위한 device global memory를 할당합니다. 이 변수들은 위에서 d_edges, d_dest, d_label에 해당합니다. 이 메모리의 내용은 cudaMemcpy를 사용하여 Host에서 Device로 복사됩니다.
그리고 어떤 정점이 frontier에 추가되었는지, 즉, 이미 방문했는지 여부를 추적하기 위해서 추가 배열 d_visited를 선언합니다. 이 배열을 사용하는 이유는 커널 함수 내에서 label에 atomic 연산을 수행해야 하는데, d_visited 배열을 따로 두고 0과 1로만 처리하는 것이 훨씬 더 간단하기 때문입니다. 따라서 방문했는지 여부를 표시하는 것(visited)와 level 정보(label)를 분리하는 것이 편리합니다.
그리고 Host 코드는 디바이스 전역 메모리에 d_frontier 배열을 디바이스 전역 메모리에 할당하는데, 이는 오직 디바이스에서만 액세스되므로 host에서의 frontier 배열은 필요가 없습니다. d_c_frontier와 d_p_frontier 포인터는 d_frontier의 처음 절반과, 두번째 절반을 가리킵니다. 두 포인터의 역할은 while 루프가 끝날 때마다 서로 바뀝니다. 또한 두 frontier 배열의 크기를 나타내는 d_c_frontier_tail 변수와 d_p_frontier_tail 변수를 할당합니다.
Host 코드에서는 d_visited의 source를 제외한 모든 요소의 값을 0으로 초기화하고, source의 값은 1로 초기화합니다. CUDA 메모리를 할당하면 기본적으로 0으로 초기화되므로, 여기서는 source의 값만 1로 초기화하였습니다. 그리고, d_c_frontier_tail 변수의 값은 0으로, d_p_frontier[0]의 값은 source, d_p_frontier_tail 변수의 값은 1, label[source]의 값은 0으로 초기화합니다. 모든 초기화 작업이 완료되면 이제 while 루프에 진입하여 커널을 실행합니다.
루프에서 수행되는 커널 함수는 다음과 같이 구현됩니다.
__global__
void BFS_Bqueue_kernel(int* p_frontier, int* p_frontier_tail, int* c_frontier, int* c_frontier_tail, int* edges, int* dest, int* label, int* visited)
{
__shared__ int c_frontier_s[BLOCK_QUEUE_SIZE];
__shared__ int c_frontier_tail_s, our_c_frontier_tail;
if (threadIdx.x == 0)
c_frontier_tail_s = 0;
__syncthreads();
const int tid = blockIdx.x*blockDim.x + threadIdx.x;
if (tid < *p_frontier_tail) {
const int my_vertex = p_frontier[tid];
for (int i = edges[my_vertex]; i < edges[my_vertex+1]; i++) {
const int was_visited = atomicExch(&(visited[dest[i]]), 1);
if (!was_visited) {
label[dest[i]] = label[my_vertex] + 1;
const int my_tail = atomicAdd(&c_frontier_tail_s, 1);
if (my_tail < BLOCK_QUEUE_SIZE) {
c_frontier_s[my_tail] = dest[i];
}
else {
c_frontier_tail_s = BLOCK_QUEUE_SIZE;
const int my_global_tail = atomicAdd(c_frontier_tail, 1);
c_frontier[my_global_tail] = dest[i];
}
}
}
}
__syncthreads();
if (threadIdx.x == 0) {
our_c_frontier_tail = atomicAdd(c_frontier_tail, c_frontier_tail_s);
}
__syncthreads();
for (int i = threadIdx.x; i < c_frontier_tail_s; i += blockDim.x) {
c_frontier[our_c_frontier_tail + i] = c_frontier_s[i];
}
}우선 커널 함수에서 사용하는 공유 메모리 배열은 무시하고 살펴보겠습니다.
커널 함수는 일단 BFS_sequential의 외부 for-루프를 병렬화합니다. 각 스레드가 p_frontier의 배열 요소 하나를 담당하여 이웃하는 정점을 처리하죠. 이를 위해서 커널 함수의 line 13에서 p_frontier에 액세스하는 것을 볼 수 있습니다. 그리고 이전에 방문하지 않은 이웃 정점을 만나면 c_frontier 배열에 추가해주는데 이것이 커널 함수의 첫 번째 for문에 해당합니다. 모든 스레드가 p_frontier 배열의 처리를 완료하면 c_frontier 배열은 새로운 frontier의 모든 정점들을 포함하고 이는 다음 반복을 위한 p_frontier가 됩니다.
커널 함수의 첫 번째 for문은 BFS_sequential 함수의 안쪽에 있는 for-루프와 유사합니다만, visited 배열의 존재 때문에 실행 효율 측면에서 작은 차이가 있습니다. BFS_sequential 함수에서 외부 for-루프에서의 각 반복은 하나의 frontier 정점의 이웃 정점들을 처리합니다. 이때, frontier 정점들은 동일한 이웃 정점을 가지고 있을 가능성이 높습니다.
예를 들어, 아래 그래프에서 level 2의 frontier 정점인 3, 4, 6은 모두 동일한 이웃 정점 8을 가지고 있습니다. BFS_sequential에서 바깥 for 루프 반복은 순차적으로 수행되고, 정점 3에서 정점 8을 방문하여 level 3으로 업데이트 하더라도 다음 루프에서 정점 4가 다시 정점 8을 방문하는 비효율적인 작업이 수행되는 것입니다.

visited 배열을 사용하게 되면 이러한 중복 방문은 제거됩니다. 위의 예제 그래프에서 정점 3이 먼저 처리되었다고 가정한다면 정점 3이 처리될 때 정점 8이 방문되었으니 visited[8]에 표시가 됩니다. 그 다음 정점 4,6이 처리될 때, 정점 8은 이미 방문되었다는 것을 알고 있으므로 c_frontier에 추가하지 않게 됩니다.
병렬 커널에서 frontier 정점은 스레드에 의해서 병렬로 처리됩니다. 스레드에 의한 전역 메모리 쓰기는 커널이 종료되거나 동기화 장벽이 있을 때까지 다른 스레드에서 visible되는 것을 보장하지 않습니다. 따라서, 각 스레드들은 서로에 의한 visited에 표시를 볼 수 없습니다. 위 예시에서 정점 3,4,6을 처리하는 스레드는 모두 병렬로 실행됩니다. 따라서 각각 스레드에서 정점 8을 level 3으로 표시하고 c_frontier에 정점을 삽입할 수 있으며, 결과적으로 정점 8이 c_frontier에 여러 번 나타날 수 있습니다. 물론 중복된 정점을 처리할 때 스레드는 동일한 작업을 수행하므로 최종 결과에는 영향을 미치지는 않지만, 그래프가 크다면 상당히 많은 정점들이 중복으로 처리가 될 수 있습니다.
이러한 중복이 발생하지 않도록 하기 위해서 atomic 연산을 사용하여 정점의 방문 상태를 표시하고 확인합니다(line 15). atomicExch를 사용하는데, 이는 두 값을 swap하는 atomic 연산이며 첫 번째 파라미터가 대상이 되는 변수이고, 두 번째 파라미터가 변경할 값이 됩니다. 따라서, 방문할 정점의 visited 값을 1로 변경하면서 이전의 값을 받아와 was_visited 변수에 저장합니다. 그리고 was_visited 값으로 이미 방문한 정점인지 확인하고, 방문하지 않은 정점에 대해서 처리를 계속합니다.
하나의 스레드 블록에서 수행되는 atomic 연산은 다른 모든 스레드 블록에서 볼 수 있습니다. 이 방법으로 정점 3,4,6에서 정점 8에 방문할 예정이라도, 오직 하나의 스레드만이 was_visited 조건을 만족하여 정점 8은 한 번만 c_frontier 배열에 삽입될 것입니다.
커널 함수에서 for 루프를 반복하며 방문한 정점을 c_frontier 배열에 추가할 때 고려해야할 사항들이 몇 가지 있습니다. 먼저 각 스레드는 c_frontier 배열에 정점을 동시에 삽입하기 때문에 업데이트가 안전하게 수행되기 위해서 c_frontier_tail 변수에 대해 read-modify-write를 수행할 때 atomic 연산을 사용할 필요가 있습니다.
두 번째는 스레드는 여러 정점들을 c_frontier 배열에 추가할 가능성이 있습니다. 이렇게 하면 병합(coalesced)할 수 없는 전역 메모리 쓰기 패턴이 생성될 수 있습니다. 이를 방지하기 위해서 공유 메모리에 버퍼(c_frontier_s)를 사용하여 블록 내 스레드에 의한 업데이트를 취합하고, 커널의 끝 부분에서 공유 메모리 버퍼에 추가된 정점들을 전역 메모리로 업데이트합니다. 이렇게 사용되는 privated한 버퍼를 block-level 큐라고 합니다. 또한, block level 큐에 정점을 삽입하기 위해 공유 메모리에 c_frontier_tail_s 변수도 생성해야합니다.
커널 함수에서 block-level 큐는 공유 메모리 배열 c_frontier_s로 선언됩니다. c_frontier_s로 값을 추가하는 것은 공유 메모리 배열 c_frontier_tail_s 변수를 통해 이루어집니다. 스레드 0에서는 커널 초반에 c_frontier_tail_s의 값을 0으로 초기화하고 __syncthreads() 호출을 통해 동기화합니다. 공유 메모리 배열은 제한된 크기를 가지고 있으므로, for 루프를 통해 c_frontier_s 배열에 정점들을 추가하다가, overflow가 발생되면 나머지 정점들은 c_frontier 배열에 직접 추가됩니다.
각 정점에서 처리되어야 하는 작업들이 완료되면, 스레드 0은 c_frontier_tail에 대해 atomic 연산을 수행하여 c_frontier에 추가할 c_frontier_s를 위한 공간을 확보합니다. 그리고 atomic 연산은 확보된 공간의 시작 인덱스를 리턴합니다. 그리고 다시 동기화를 시켜주고, 다음 for-루프를 통해 c_frontier_s 배열에 존재하는 값들을 c_frontier 배열로 옮겨줍니다.
block-level 큐의 내용이 전역 메모리의 큐로 복사되는 동작을 아래 그림에서 보여주고 있습니다.
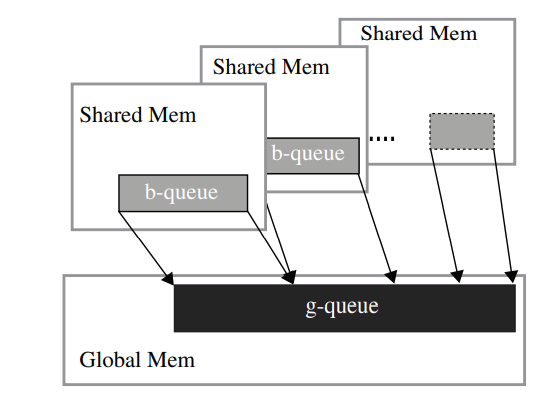
커널 함수로 BFS를 수행하면, sequential BFS와 동일한 결과를 얻을 수 있습니다.
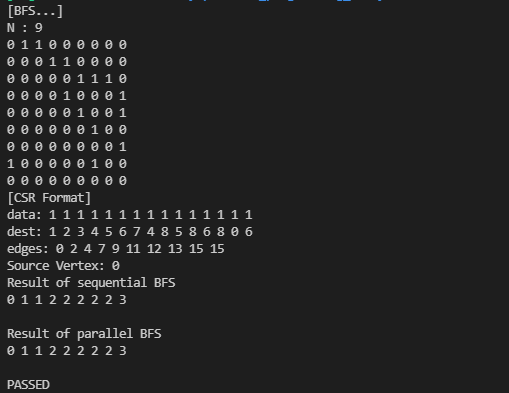
전체 코드는 마찬가지로 아래 링크에서 확인하실 수 있습니다.
https://github.com/junstar92/parallel_programming_study/blob/master/CUDA/BFS/bfs.cu
GitHub - junstar92/parallel_programming_study: Study parallel programming - CUDA, OpenMP, MPI, Pthread
Study parallel programming - CUDA, OpenMP, MPI, Pthread - GitHub - junstar92/parallel_programming_study: Study parallel programming - CUDA, OpenMP, MPI, Pthread
github.com
Optimization
위에서 구현한 BFS_Bqueue 커널에서 BFS를 병렬로 수행할 수 있었지만, 성능과 효율성 측면에서 몇 가지 개선할 영역들이 존재합니다. 이론적으로 어떠한 영역에서 개선할 수 있는지 살펴보도록 하겠습니다.
Memory Bandwidth
커널 함수에서 스레드에 frontier 정점을 할당할 때, 각 스레드는 for 루프에서 두 개의 연속된 위치의 edges 배열 요소에 접근합니다. 그 다음 다수의 연속된 dest 배열 위치에 액세스합니다.
for (int i = edges[my_vertex]; i < edges[my_vertex+1]; i++)그런 다음에는 dest 요소 값에 인덱싱되는 다소 랜덤한 위치의 label 배열 요소들에 액세스합니다. 이는 인접한 스레드들이 edges, dest, label 배열에 액세스할 때 인접한 전역 메모리 위치를 액세스하지 않는다는 것을 의미하고, 이러한 액세스는 병합되지 않습니다. 이는 Texture Memory(텍스처 메모리)를 사용하여 해결할 수 있는데, 아직 텍스처 메모리에 대해서 자세히 알아보지 않았기 때문에 관련된 내용은 다른 포스팅을 통해 추후에 알아보도록 하겠습니다.
아래 그림은 level-2 frontier 정점들에 대한 전역 메모리 액세스 패턴을 보여줍니다. 여기서 source는 정점 2입니다.

level-2 frontier 정점은 0과 8로 두 개가 있습니다. 스레드 0과 1이 이 정점들을 처리한다고 가정해보겠습니다.
p_frontier 배열의 액세스 패턴은 병합적입니다. 그 다음 edges 배열에 대한 액세스는 병합되지 않은 것을 볼 수 있습니다. 처음에 스레드 0은 edges[0]에 액세스하고 스레드 1은 edges[8]에 액세스합니다. 즉, 연속된 메모리 위치에 액세스하지 않습니다. 그 다음 스레드 0은 edges[1], 스레드 1은 edges[9]에 액세스하므로 이 또한 연속된 위치의 액세스가 아닙니다.
edges 요소 값에 기반하여 스레드 0은 dest[0]과 dest[1]에 액세스하는 반면, 스레드 1은 정점 8로부터 나가는 간선이 없기 때문에 어떠한 액세스도 없습니다. 있다고 하더라도 스레드 0에서 액세스하는 요소와 연속된 위치는 아닐 것입니다.
그런 다음 스레드 0은 dest[0]과 dest[1] 값에 기반하여 label 배열에 액세스합니다. 이 예제에서는 label[1]과 label[2]에 액세스합니다.
일반적으로 그래프의 모양과 정점에 번호가 매겨진 방식에 따라 임의의 거리에 있는 위치에 액세스합니다. 명백한 것은 label 배열에 대한 액세스가 일반적으로 병합되지 않는다는 것입니다. 따라서, edges, dest, label 배열에 대한 액세스는 텍스처 메모리를 통해 이루어져야 합니다.
Hierarchical Queues
커널 함수의 block-level 큐인 c_frontier_s는 hierarchical queue 디자인의 example입니다. 일반적으로 많은 수의 병렬 스레드로부터 삽입 요청을 수신하는 큐가 있을 때, tail 변수에 대한 atomic 연산은 과도한 경쟁을 발생시켜 이러한 스레드들이 순차적으로 수행되도록 만들 수 있습니다.
각 블록에 private한 큐를 만들어주면 큐 삽입에서의 경쟁이 크게 줄어듭니다. 다만, 커널의 마지막 부분에서 private 큐의 내용을 global 큐에 통합하는 추가적인 단계(코스트)가 필요합니다.
하지만, block-level 큐 또한 과도한 경쟁이 발생할 수 있습니다. 이는 워프의 모든 스레드가 block-level 큐에 액세스할 때 경쟁이 반드시 발생하기 때문입니다. 동일한 워프에 있는 모든 스레드들은 어느 시점에서나 동일한 명령을 수행하기 때문에, 해당 스레드들은 모두 동시에 atomic 연산을 수행하고 이는 과도한 경쟁으로 이어집니다. 이러한 경쟁은 워프에서 스레드의 실행을 순차적으로 수행하도록 만들고, 실행 속도를 크게 감소시킵니다.
각 워프 내부의 경쟁은 아래 그림과 같이 계층에 다른 level의 큐(w-queue)를 추가하여 해결할 수 있습니다.

이러한 워프 수준 큐의 수는 일반적으로 2의 제곱이며, 이는 조정이 가능한 매개변수 영역입니다. 커널 실행 중에 우리는 threadIdx.x 값의 최하위 비트를 사용하여 w-queue의 수와 동일한 수로 스레드를 분류합니다. 이는 워프의 스레드들에 의해서 실행되는 atomic 연산을 w-queue에 균등하게 분배하기 위함입니다.
예를 들어, 4개의 w-queue가 있는 경우 모든 스레드를 threadIdx.x 값의 최하위 2비트를 사용하여 분류합니다. threadIdx.x 값의 최하위 2비트가 00인 스레드들은 w-queue 0에 액세스합니다. 블록에 64개의 스레드가 있다고 가정한다면 w-queue 0에 액세스하는 16개의 스레드는 0, 4, 8, 12, ..., 56, 60 입니다. 64개의 스레드이므로 여기에는 2개의 워프가 있습니다. 워프 1에서 32개의 스레드 중에 8개가 w-queue 0에 액세스하고, 이러한 스레드는 32, 36, 40, 44, 48, 52, 56, 60 입니다. 요지는 워프에서 atomic 연산을 실행할 때마다 워프 내 스레드들의 1/4이 w-queue 0에 액세스한다는 것입니다. 마찬가지로 w-queue 1에 액세스하는 16개의 스레드는 1, 5, 9, 13, ..., 57, 61 입니다. 따라서, 총 스레드의 1/4이 w-queue 1에 액세스합니다.
커널의 마지막 부분에서는 위 그림과 같이 w-queue의 내용을 b-queue에 통합해야 합니다. 그런 다음 b-queue의 내용을 위에서 살펴본 BFS_Bqueue_kernel의 마지막 부분과 같이 g-queue에 통합합니다.
w-queue의 수를 늘리면 각 w-queue에 대한 경쟁 수준을 줄일 수 있습니다. 하지만 더 많은 w-queue를 가지는데 비용이 있으며, w-queue의 수를 늘리면 각각의 w-queue에서의 크기는 작아집니다. 이렇게 되면 큐 중의 하나가 오버플로우될 확률이 높아집니다. 따라서 스레드는 block-level 큐에서 살펴본 것처럼 w-queue의 오버플로우 상태를 체크하고 오버플로우가 발생하면 b-queue로 직접 추가해야합니다.
Kernel Launch Overhead
대부분의 그래프에서 BFS의 처음 몇 번의 반복의 frontier는 꽤 적습니다. 첫 번째 반복의 frontier는 source의 이웃만을 포함하고 있습니다. 그리고 다음 반복의 frontier는 현재 frontier 정점들의 모든 이웃을 가지고 있습니다. 이러한 초기 반복에서 커널 실행의 오버헤드가 병렬화의 이점보다 클 수 있습니다. 일반적으로 frontier의 크기는 한 반복의 정점들에서 나가는 간선의 평균 수만큼 증가합니다.
이러한 초기 반복을 처리하는 한 가지 방법은 하나의 스레드 블록으로만 실행되는 다른 커널을 준비하는 것입니다. 이 커널은 오버플로우가 발생했을 때를 제외하고 b-queue만을 사용합니다. 이 커널은 while 루프의 초반 부분을 수행하는데, froniter가 b-queue를 오버플로우하는 크기에 도달하면 커널은 block-level 큐의 내용을 g-queue에 복사하고 호스트 코드로 돌아갑니다. 그리고 호스트 코드는 이후 반복에서 일반적인 커널을 실행합니다.
즉, 따로 준비한 커널로 초기 반복을 수행하여 오버헤드를 제거하고, 오버헤드보다 병렬화의 이점이 더욱 커지는 시점에 원래 사용하던 커널로 반복을 수행하는 것입니다.
Load Balance
각 스레드에 의해 수행될 작업의 양은 할당된 정점의 간선에 따라서 달라집니다. 소셜 네트워크와 같은 일부 그래프에서 일부 정점(유명인사)은 다른 정점들보다 몇 배 더 많은 간선을 가질 수 있습니다. 이런 경우, 하나 이상의 스레드가 지나치게 오래 걸리고 전체 스레드 그리드의 실행 속도가 느려질 수 있습니다. 이는 병렬 컴퓨팅에서 load imbalance의 극단적인 예입니다. 이러한 문제는 극단적으로 많은 수의 간선을 가지는 정점을 마주한 스레드가 다시 커널을 실행하고 많은 스레드를 사용하여 그 정점을 처리할 수 있도록 하여 해결할 수 있습니다.
이렇게 스레드가 호스트없이 새로운 커널을 실행할 수 있도록 하는 메커니즘을 동적 병렬화(Dynamic Parallelism)이라고 하며, 이에 관해서 다음 포스팅에서 살펴보도록 하겠습니다.
'NVIDIA > CUDA' 카테고리의 다른 글
| WARP Execution (3) | 2022.01.05 |
|---|---|
| CUDA Dynamic Parallelism (동적 병렬) (2) | 2022.01.01 |
| Parallel Merge Sort (merge operation) (0) | 2021.12.24 |
| Sparse Matrix Computation (0) | 2021.12.21 |
| Parallel Histogram (0) | 2021.12.18 |




댓글