References
- Programming Massively Parallel Processors
Contents
- Kogge-Stone Scan 알고리즘
Background
수학적으로 inclusive scan 연산은 binary associative operator \(\oplus\)와 n개의 input 배열 \([ x_0, x_1, \cdots, x_{n-1} ]\)을 취해서 아래의 output 배열을 반환하는 연산입니다.
\[ [x_0, (x_0 \oplus x_1), \cdots, (x_0 \oplus x_1 \oplus \cdots x_{n-1}) ] \]
만약 \(\oplus\)가 덧셈 연산이라면 [3 1 7 0 4 1 6 3]의 input 배열에 대한 inclusive scan 연산은 [3 4 11 11 15 16 22 25]를 반환합니다.
inclusive scan 연산은 40인치의 소시지를 8명의 사람이 각각 3, 1, 7, 0, 4, 1, 6, 3 인치씩 주문했다고 했을 때, 소시지를 자르는 지점을 빠르게 계산하는데 사용할 수 있습니다. 즉, 한 그룹의 주문을 받아서 주문이 한 번에 처리될 수 있는 모든 절단 지점을 식별하는 것이고, 주문은 위 예시처럼 소시지가 될 수도 있고, 컴퓨터의 메모리가 될 수 있습니다. 모든 절단 포인트를 빠르게 계산할 수 있다면 주문도 병렬로 처리할 수 있습니다.
exclusive scan 연산은 inclusive scan과 유사한데, 반환하는 배열은 다음과 같습니다.
\[ [0, x_0, (x_0 \oplus x_1), \cdots, (x_0 \oplus x_1 \oplus \cdots x_{n-2}) ] \]
첫 번째 output 원소는 0이고, 따라서 마지막 output 원소는 \(x_{n-1}\)까지가 됩니다.
exclusive scan의 사용은 inclusive scan과 유사한데, 약간 다른 정보를 제공합니다.
소시지 예시에서 exclusive scan은 [0 3 4 11 11 15 16 22]를 반환하는데, 이는 절단 지점의 시작점입니다. 예를 들어 첫 번째 사람은 0인치에서 시작하고, 마지막 사람은 22인치 지점에서 시작합니다. 이렇게 시작점의 정보는 메모리 할당과 같은 곳에서 유용하며 할당된 메모리의 시작점에 대한 포인터를 반환될 수 있습니다.
inclusive scan과 exclusive scan 간의 변환은 쉽습니다. 단순히 모든 원소들을 shift하고 채우기만하면 됩니다.
inclusive scan을 exclusive scan으로 변환하려면 모든 원소를 오른쪽으로 shift하고 첫 번째 요소에 0을 채우면 됩니다.
exclusive scan을 inclusive scan으로 변환하는 것은 모든 원소들을 왼쪽으로 shift하고 마지막 원소는 input의 마지막 원소의 값으로 채우면 됩니다.
이러한 병렬 scan은 radix sort, quick sort, string 비교, polynomial evaluation 등의 병렬 알고리즘에서 주요 연산으로 사용됩니다.
병렬 scan 알고리즘을 살펴보기 전에 연산이 덧셈이라고 가정하고 효율적인 시퀀스 scan 알고리즘을 살펴보겠습니다. 이 알고리즘은 input은 x 배열이고 output은 y 배열에 저장됩니다.
void sequential_scan(float* X, float* Y, int n)
{
int accumulator = X[0];
Y[0] = accumulator;
for (int i = 1; i < n; i++) {
accumulator += X[i];
Y[i] = accumulator;
}
}위 알고리즘은 각 input, output 요소에 대해 아주 작은 양의 작업만 수행하므로 꽤 효율적이라고 볼 수 있습니다. 좋은 컴파일러에서는 각 input x 원소에 대해 오직 한 번의 덧셈, 한 번의 메모리 로드 한 번의 메모리 저장만이 사용됩니다. 이 정도의 작업은 해야되는 최소한의 작업입니다.
A Simple Parallel Scan (Kogge Stone Scan)
먼저 각 output 원소에 대해 reduction 연산을 수행하는 간단한 병렬 inclusive scan 알고리즘을 살펴보겠습니다. 이 알고리즘의 주 목적은 각 output 원소를 계산하는데 관련된 input 원소의 reduction 트리를 계산하여 빠르게 각 요소를 생성하는 것입니다. 각 output 원소에 대한 reduction 트리는 여러 가지 방법으로 디자인될 수 있는데, 첫 번째로 알아볼 방법은 1970년대 fast adder 회로 설계를 위해 발견된 Kogge-Stone 알고리즘입니다.

위 그림은 input 원소들을 포함하고 있는 XY 배열에서 연산하는 in-place scan 알고리즘을 보여주고 있습니다. 반복적으로 XY 배열의 결과를 output 원소로 저장하는 것을 볼 수 있습니다. 이 알고리즘에서는 알고리즘 시작 전에 XY[i]의 값이 input 원소 \(x_i\)의 값이라고 가정합니다. n번째 반복 끝에서 XY[i]는 \(2^n\)개의 input 원소에 대한 합이 됩니다.
즉, iteration 1에서 XY[i]의 값은 \(x_{i-1} + x_i\)이고, iteration 2에서 XY[i]는 \(x_{i-3} + x_{i-2} + x_{i-1} + x_{i}\)가 됩니다.
위 그림은 16개의 원소를 가진 input에서 알고리즘의 각 스텝을 보여줍니다. 각 세로줄은 XY 배열의 원소를 의미하고, 가장 왼쪽편에 위치한 선이 XY[0]이 됩니다. 진행 순서는 위에서 아래로 가면서 진행합니다. 첫 번째 iteration에서 XY[0] 이외의 각 위치에서 위 그림의 첫 번째 행에 표시된 것과 같이 현재 값과 왼쪽에 인접한 값의 합이 계산됩니다. 예를 들어, 첫 번째 iteration 후에 XY[3]은 \(x_2 + x_3\)이 되고, 위 그림에서는 \(\sum x_2...x_3\)으로 표시되어있습니다. XY[1]은 \(x_0 + x_1\)되고, 최종답이기 때문에 이어지는 iteration에서 이 값은 더이상 변경되지 않습니다.
두 번째 iteration에서 XY[0]과 XY[1] 이외의 각 위치에서 위 그림의 두 번째 행에서 보여주는 것처럼 현재 값과 2칸 떨어져 있는 위치의 합을 계산합니다. 따라서 XY[i]는 현재 반복에서 \(x_{i-3} + x_{i-2} + x_{i-1} + x_i\)가 됩니다. 두 번째 반복이후 XY[3]은 \(\sum x_0 ... x_3\), 즉, \(x_0+x_1+x_2+x_3\)이 되고, XY[2]와 XY[3]은 최종답이기 때문에 마찬가지로이어지는 iteration에서 더이상 변경되지 않습니다. 나머지 반복도 이와 유사한 방식으로 진행됩니다.
이제 위에서 설명한 알고리즘을 병렬로 구현해보겠습니다.
https://github.com/junstar92/parallel_programming_study/blob/master/CUDA/prefixSum/prefixSum.cu
GitHub - junstar92/parallel_programming_study: Study parallel programming - CUDA, OpenMP, MPI, Pthread
Study parallel programming - CUDA, OpenMP, MPI, Pthread - GitHub - junstar92/parallel_programming_study: Study parallel programming - CUDA, OpenMP, MPI, Pthread
github.com
(아래 코드는 설명을 위해 간단히 작성된 것이고, 경계 검사 등을 제대로 수행하지 않았습니다. 자세한 코드는 깃헙 링크를 참조하시길 바랍니다.)
__global__ void koggeStone(float* X, float* Y, int n)
{
__shared__ float XY[SECTION_SIZE];
int i = blockIdx.x*blockDim.x + threadIdx.x;
if (i < n)
XY[threadIdx.x] = X[i];
for (unsigned int stride = 1; stride < blockDim.x; stride *= 2) {
__syncthreads();
if (threadIdx.x >= stride)
XY[threadIdx.x] += XY[threadIdx.x - stride];
}
Y[i] = XY[threadIdx.x];
}우선 전체가 아닌 병렬로 수행될 하나의 섹션만 고려하고 그 섹션의 크기는 컴파일 시간에 결정되는 SECTION_SIZE로 정의하겠습니다. 하나의 XY 원소를 구하는데 하나의 스레드를 할당하도록 하고, 블록을 구성하는 스레드의 크기는 SECTION_SIZE가 됩니다. 하나의 섹션에 포함되는 원소들만 포함하는 배열에 대해 결과가 계산되므로, 나중에 원본 배열에 대한 각 섹션별 scan 결과를 합쳐주는 작업이 필요합니다.
각 섹션, 즉, 블록에서 스레드들이 협동하여 X 배열의 원소들을 공유 메모리 XY 배열에 로드하도록 하겠습니다. 이 작업은 각 스레드가 담당하는 output 배열의 원소 위치에 대한 전역 데이터 인덱스인 i = blockIdx.x*blockDim.x + threadIdx.x를 계산하여 수행할 수 있습니다. 각 스레드는 해당 인덱스 위치의 input 원소를 공유 메모리로 로드합니다. 이 과정이 코드의 line 3-6에 해당됩니다.
그리고 각 루프는 스레드에 할당된 XY 배열 위치에 대한 reduction tree를 반복합니다. line 8부터가 이 부분에 해당하고, 각 루프에서 모든 스레드가 reduction tree에서 이전 단계의 add를 완료했는지 확인하기 위해 __syncthreads()를 호출하여 동기화해줍니다. 루프 내에서는 각 반복에서 누적되어야 하는 인덱스를 검사하기 위해 line 10에서 if문을 통해 체크하고 있습니다.
코드의 for 루프에서의 동작은 위의 그림의 동작과 일치합니다. 알고리즘을 살펴보면 앞쪽에 위치하는 XY는 뒤쪽에 위치하는 XY보다 일찍 끝납니다. 이 동작은 stride의 값이 작을 때 첫 번째 워프에서 어느 정도 제어 발산을 유발합니다. 그리고 인접한 스레드는 거의 동일한 수의 반복을 수행하는 것을 확인할 수 있습니다.
inclusive scan을 쉽게 exclusive scan으로 변환할 수 있는데, 커널 내에 공유 메모리 XY에 입력 배열 값을 로드할 때 다음과 같이 변경해주면 됩니다.
if (i < n && threadIdx.x != 0) {
XY[threadIdx.x] = X[i-1];
}
else {
XY[threadIdx.x] = 0;
}
위 코드의 속도와 작업 효율을 분석해보겠습니다. 모든 스레드는 \(log_2 N\) 스텝까지 반복을 수행합니다. 여기서 N은 SECTION_SIZE 입니다. 각 iteration에서 수행되지 않는 스레드의 수는 stride의 크기와 같습니다. 따라서, 알고리즘에서 작업을 수행하고 완료하는 횟수는
\[\sum (\text{N - stride}), \text{ for strides 1,2,4,...,N/2}\]
입니다. 첫 번째 항인 N은 stride의 값에 독립적이므로 \(N*log_2 N\)으로 계산되고, 두 번째 항은 기하급수로 계산하여 N-1이 됩니다. 즉, 작업의 총 횟수는
\[N*log_2 N - (N-1)\]
이 됩니다.
Sqeuntial Scan 알고리즘에서 for 루프의 반복 횟수는 N-1입니다. 적당한 크기의 섹션에서 Kogge Stone Scan 알고리즘은 Sequential Scan보다 훨씬 더 많은 작업을 수행합니다. 만약 512개의 원소가 있다면 커널 함수는 대략 Squential Scan 함수보다 약 8배 더 많은 작업을 수행합니다. 이 비율은 N이 커질수록 증가합니다.
실행 속도 측면에서 Sequential Scan의 for-루프는 N번의 반복을 수행합니다. 커널 코드의 경우에는 각 스레드에서 for-루프는 \(log_2 N\)번 반복합니다. 실행에 필요한 리소스에 제한이 없다면 커널 함수의 실행 속도는 Sequential 함수의 약 \(\frac{N}{log_2 N}\)배가 됩니다. N이 512인 경우에는 \(\frac{512}{9} = 56.9\)배가 됩니다.
실제 CUDA 디바이스에서 Kogge Stone 커널에 의해 수행되는 작업의 양은 이론적 수치인 \(N*log_2 N - (N-1)\)보다 많습니다. 반복되면서 많은 스레드들이 for-루프에서의 연산을 하지 않지만, 스레드 블록이 실행을 완료할 때까지 그 리소스를 소비합니다. 따라서, 현실적으로 실행 리소스의 양은 \(N*log_2 N\)에 가깝습니다.
Time Unit이라는 개념은 Scan 알고리즘 간의 비교를 위한 대략적인 실행 시간의 지표로 사용됩니다. Sequential Scan에서 N개의 입력 원소를 처리하는데에는 약 N개의 time unit이 필요합니다. 예를 들어, 1024개의 입력 원소가 있다면 이를 처리하는데 1024개의 time unit이 필요합니다.
CUDA 디바이스에서 P execution units(streaming processor)를 사용하면, 커널 함수는 \(\frac{N*log_2 N}{P}\) time unit 동안 실행될 것으로 예상할 수 있습니다. 예를 들어, 1024개의 스레드와 32개의 execution units을 사용하여 1024개의 입력 원소를 처리할 경우 커널은 \(\frac{1024*10}{32} = 320\)의 time unit이 필요합니다.
따라서 Sequential Scan에 비해 Kogge Stone Scan을 사용하면 약 1024/320 = 3.2의 속도 향상을 이끌어낼 수 있다고 추측할 수 있습니다.
Sequential 코드에 비해서 Kogge Stone 커널은 두 가지 면에서 문제점이 있습니다.
첫번째는 병렬 커널을 실행하기 위한 하드웨어의 사용이 덜 효율적입니다. Sequential Scan 보다 더 효율적으로 동작하기 위해서는 최소 8배 더 많은 execution time을 필요로 합니다.
두 번째, 추가적인 덧셈 작업이 필요합니다. 각 스레드 블록은 해당 블록에서의 reduction만 수행하므로, 커널을 수행한 뒤에 Host에서 추가적으로 더하는 작업이 필요합니다.
입력의 크기가 4096일 때, 결과를 보면

Sequential Code에서 더 좋은 성능을 보여주고 있습니다.
크기를 조금 더 크게 늘려서 1,000,000개의 입력으로 실행했을 때, 겨우 Sequential Code의 성능보다 조금 더 좋아졌습니다.
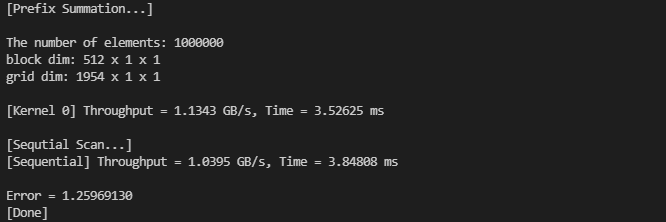
하지만 Convolution 때의 결과처럼, GPU를 사용한다고 해서 드라마틱한 성능의 차이는 보여주지 않았습니다... 특히 입력이 1,000,000보다 더 컸지만 비등비등한 성능을 보여주기도 했습니다.
하드웨어 차이인가 궁금해서 RTX 3080으로 돌려봤는데, 이 경우에는 GPU를 사용한 경우가 확실히 더 좋은 성능을 보여주고 있습니다.
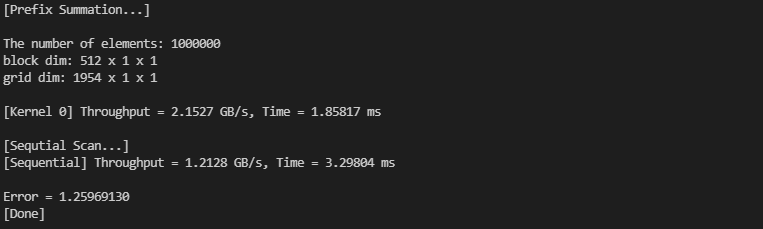
입력의 수가 더 커지면, 성능 향상은 더욱 큽니다.

다음 포스팅에서는 더 효율적인 알고리즘을 알아보도록 하겠습니다.
'NVIDIA > CUDA' 카테고리의 다른 글
| Parallel Histogram (0) | 2021.12.18 |
|---|---|
| Parallel Prefix Sum (2) (0) | 2021.12.17 |
| Tiled 2D Convolution (0) | 2021.12.14 |
| 1D Convolution (CUDA Constant Memory) (1) | 2021.12.13 |
| 부동소수점 (Floating-Point) (0) | 2021.12.11 |




댓글