References
- Programming Massively Parallel Processors
Contents
- 1D, 2D Convolution
- 1D Parallel Convolution (Basic)
- Constant Memory and Caching
- Tiled 1D Convolution with Halo cells(ghost cells)
Convolution(컨볼루션)은 signal processing(신호 처리), digital recoding, image/video processing(이미지/영상 처리), computer vision 등에서 다양한 형태로 사용되는 배열 연산(array operation)입니다. 아마도 딥러닝의 CNN에 대해서 공부를 했다면 조금 더 쉽게 다가올 수 있을 것 같습니다. 아래 포스팅은 CNN에 대해 정리한 글입니다.. !
Convolutional Neural Network(CNN)
Convolution이 사용되는 분야에서 컨볼루션은 신호나 픽셀을 보다 바람직한 값으로 변환시켜주는 필터로 동작합니다. 아래 포스팅에서 언급하는 이미지 블러를 수행하는 커널이 바로 이러한 필터를 사용하였습니다.
CUDA Thread 구조와 Data Mapping (예제 : 이미지 흑백, Blur 처리)
다른 예로, 가우시안 필터(Gaussian Filter)는 이미지에서 물체의 경계와 가장자리를 선명하게 하는데 사용되는 Convolution Filter입니다.
Background (1D, 2D Convolution)
Convoltion은 output 데이터 요소가 input 데이터 요소의 인접한 요소들과의 가중치 합(weighted sum)인 배열 연산입니다. 여기서 사용되는 가중치는 일반적으로 Convolution Kernel(컨볼루션 커널) 이라고 하는 마스크 배열에 의해 정의됩니다. CUDA 커널과 이름이 동일하기 때문에 혼동이 발생할 수도 있으니.. 유의바랍니다.. !
오디오 디지털 신호 처리에서의 입력 데이터는 1차원 형태이고 시간에 대한 함수로 샘플링된 신호의 볼륨을 나타냅니다. 아래 그림은 7개 요소를 가진 입력 배열 N에 5개의 요소를 가진 컨볼루션 커널 M이 적용되는 컨볼루션 예시를 보여주고 있습니다.

위 그림처럼 P[2]의 값은 N[0]에서 N[4]까지의 가중합으로 계산됩니다. N 원소의 값을 1,2,3,...7 이라고 가정합니다. M 원소는 가중치를 정의하는데, 그 값들이 3,4,5,4,3이라고 가정하겠습니다. 이 가중치들은 각 위치에 해당하는 N 원소 값에 곱하여 더해집니다. 따라서, P[2]에 대한 계산은 다음과 같습니다.
\[\begin{align*} P[2] &= N[0]*M[0] + N[1]*M[1] + N[2]*M[2] + N[3]*M[3] + N[4]*M[4] \\ &= 1*3 + 2*4 + 3*5 + 4*4 + 5*3 \\ &= 57 \end{align*}\]
일반적으로 컨볼루션 커널의 크기는 홀수인 경향이 있는데, 이는 계산되는 요소를 중심으로 대칭적으로 가중합을 계산해주기 때문입니다. 즉, 계산되는 요소 양쪽으로 동일한 수의 요소를 포함하도록 해줍니다.
P[i]에 대한 계산은 N[i-2]부터 시작하는 부분배열과 M배열 사이의 Inner Product(내적)으로 볼 수 있습니다.
다음 이미지는 P[3]에 대한 컨볼루션 연산을 보여줍니다.

즉, P[3]의 값은 N[1]부터 N[5]의 가중치합이 되며, 아래처럼 계산됩니다.
\[\begin{align*} P[3] &= N[1]*M[0] + N[2]*M[1] + N[3]*M[2] + N[4]*M[3] + N[5]*M[4] \\ &= 2*3 + 3*4 + 4*5 + 5*4 + 6*3 \\ &= 76 \end{align*}\]
컨볼루션은 주변 원소를 포함한 가중치 합이기 때문에 배열에 끝에 가까운 output 원소에 대해서는 경계 조건(boundary condition)이 발생할 수 있습니다. 아래 이미지와 같이, P[1]을 계산할 때에 P[1] 왼쪽에는 N 원소가 하나만 존재합니다. 즉, 컨볼루션에 대한 정의에 따르면 P[1]을 계산하기에는 N의 원소가 충분하지 않습니다. 이러한 경계 조건에서는 일반적으로 누락된 N의 원소를 정의해주어서 해결하는데, 일반적으로 누락된 원소의 기본값은 0입니다.

오디오 신호 처리 예시의 경우에는 녹음 시작 전과 종류 후의 신호 볼륨이 0이라고 가정할 수 있습니다. 이 경우 P[1]의 계산은 다음과 같습니다.
\[\begin{align*} P[3] &= 0*M[0] + N[0]*M[1] + N[1]*M[2] + N[2]*M[3] + N[3]*M[4] \\ &= 0*3 + 1*4 + 2*5 + 3*4 + 4*3 \\ &= 38 \end{align*}\]
P[0]의 계산에서는 두 개의 N의 원소가 누락되어 0으로 처리될 것입니다. 이렇게 누락된 원소를 일반적으로 'ghost cells' 또는 'halo cells'라고 부릅니다. 병렬 계산에서 타일링을 사용하기 때문에 다른 유형의 ghost cell도 있습니다. 이러한 ghost cell은 타일링의 효과나 효율성에 큰 영향을 미칠 수 있는데 이 내용은 뒤에서 살펴보도록 하겠습니다.
(항상 ghost cell의 값이 0은 아닙니다. 일부 분야에서는 ghost cell의 가장 가까운 유효한 데이터의 값으로 설정합니다.)
이미지 처리나 컴퓨터 비전 분야에서 입력 데이터는 일반적으로 x-y 공간의 픽셀로 이루어진 2차원 배열입니다. 따라서, 이미지 컨볼루션은 2D Convolution입니다. 2D 컨볼루션에서의 커널은 2차원 배열이고, 커널의 x, y축은 가중치합 계산에 포함할 주변 원소의 범위를 결정합니다. 아래 그림에서는 5x5 커널을 사용했습니다.
(2D 컨볼루션 커널이 꼭 정사각형일 필요는 없습니다.)

output 원소를 계산하기 위해서, 먼저 input 배열 N에 대응되는 원소를 중심으로하는 부분배열을 취해야합니다. 그런 다음 컨볼루션 커널의 원소와 input 이미지 배열의 원소 간의 곱셈(pairwise)을 수행합니다. 위의 이미지에서 N에서 취한 5x5 부분 배열과 컨볼루션 커널의 가중치합을 보여주고 있습니다. \(P_{2,2}\)의 계산을 보여주고 있는데, C 배열 스타일 주소로 표현된 N[y][x]을 \(N_{y,x}\)로 표현하겠습니다. 실제 코드에서는 N과 P가 동적 배열일 가능성이 훨씬 높기 때문에, 실제 코드에서는 선형화된 인덱스를 사용합니다. 여기서는 2차원 인덱스로 표현합니다!
따라서, P[2][2]는 아래처럼 계산됩니다.

1D 컨볼루션과 마찬가지로 2D 컨볼루션도 경계조건을 처리해야합니다. 아래 그림은 누락된 N 배열의 요소를 0으로 처리하고 있는 것을 보여주고 있습니다.

1D Parallel Convolution
다시 1D 컨볼루션으로 돌아와서 컨볼루션 연산을 수행하는 간단한 커널 함수를 작성해보겠습니다.
1D 컨볼루션 커널 함수는 입력 배열 N, 컨볼루션 커널 M, 출력 배열 P, 그리고 컨볼루션 커널의 Kernel_Width, 입력과 출력 배열의 크기 Width를 입력으로 받을 것입니다. 따라서 1D 컨볼루션을 수행하는 커널 함수는 다음과 같이 작성될 수 있습니다.
__global__ void convolution1D_basic(float* N, float* M, float* P, int Kernel_Width, int Width)
{
int i = blockIdx.x*blockDim.x + threadIdx.x;
float Pvalue = 0.f;
int N_start_point = i - (Kernel_Width/2);
for (int j = 0; j < Kernel_Width; j++) {
if (N_start_point + j >= 0 && N_start_point + j < Width)
Pvalue += N[N_start_point + j] * M[j];
}
if (i < Width)
P[i] = Pvalue;
}변수 Pvalue을 사용하고 있는데, 모든 중간 결과들이 레지스터에 누적되므로 DRAM의 대역폭을 절약할 수 있습니다.
for 루프에서 output P 원소에 대한 인접 원소들의 가중치합을 누적하며, loop의 if문은 N 배열의 인접 원소들이 ghost cells인지를 테스트합니다. 여기서는 ghost cell의 기본값이 0이라고 가정하였기 때문에 ghost cell인 경우 가중치합을 생략합니다. 가중치합을 모두 구한 뒤에는 output P 원소에 값을 저장하며 커널 함수는 종료됩니다.
위의 커널 함수에 대해서 살펴보면, control flow 분기(divergence)가 있습니다. line 8에서 인접 원소들이 ghost cell인지 판단하는 부분에서 ghost cell이 존재한다면 인접한 스레드들은 서로 다른 분기를 따르게 됩니다. 따라서 P[0]을 계산하는 스레드에서는 곱셈 누적 합을 계산하는 line 9를 2번 스킵하고, P[1]에서는 1번 스킵합니다. 분기에 의한 cost는 입력 배열의 크기와 컨볼루션 커널의 크기에 따라 달라집니다. 큰 입력 배열과 작은 컨볼루션 커널을 사용한다면, 분기는 가장자리에 위치하는 원소들에게만 발생하여 분기에 의한 영향은 미미합니다. 컨볼루션은 보통 큰 이미지나 공간 데이터를 사용하기 때문에 일반적으로 그 효과는 미미할 것으로 예상됩니다.
이보다 더 큰 문제는 바로 메모리 대역폭입니다. 전역 메모리 액세스에 대한 부동소수점 연산의 비율은 커널 함수에서 1.0입니다. 따라서, 최적화되지 않은 행렬 곱셈 커널처럼 디바이스 성능을 온전히 사용하지 못합니다.
Constant Memory and Caching
컨볼루션 배열 M이 컨볼루션 연산에 사용될 때 3가지 특징이 있습니다.
첫번째는 배열 M의 크기는 일반적으로 작습니다. 대부분의 컨볼루션 커널의 크기는 각 차원에서 10개 미만의 원소들로 이루어집니다. 3D 컨볼루션의 경우에도 커널에는 일반적으로 1000개 미만의 원소들로 구성됩니다.
두번째로, 커널 M의 값은 실행 중에 변경되지 않습니다.
세번째, 모든 스레드가 이 커널 M 원소에 액세스합니다. 게다가, 모든 스레드는 M의 원소를 loop의 반복을 통해 M[0]부터 하나씩 순서대로 엑세스합니다.
이러한 특징은 컨볼루션 커널은 상수 메모리(Constant Memory)와 캐싱(caching)으로 만들 수 있도록 해줍니다.
아래 이미지는 CUDA 디바이스의 메모리 모델입니다.

CUDA의 메모리 Access와 Type (예제 : matrix multiplication)
위 포스팅에서 언급했듯이 CUDA 프로그래밍 모델은 개발자가 상수 메모리에 직접 변수를 선언할 수 있도록 해줍니다. 전역 메모리 변수와 마찬가지로 상수 메모리 변수도 모든 스레드 블록에서 접근이 가능합니다. 전역 메모리와의 주요 차이점은 커널 실행 중에는 스레드에 의해 상수 메모리 변수가 변경될 수 없다는 것입니다. 또한 상수 메모리의 크기는 64KB로 매우 작습니다.
상수 메모리를 사용하려면 host 코드에서 상수 메모리 변수를 할당하고 복사해야하는데, 이 방법은 전역 메모리 변수와는 다릅니다. 배열(커널) M을 상수 메모리에 선언하기 위해서 host 코드에서는 다음과 같이 전역 변수로 M을 선언합니다.
#define MAX_KERNEL_WIDTH 10
__constant__ float M[MAX_KERNEL_WIDTH];이 선언은 전역 변수 선언이므로 소스 파일 내의 함수 바깥에 위치해야합니다. 키워드 __constant__는 컴파일러에게 배열 M이 디바이스 상수 메모리에 위치해야한다는 것을 알려줍니다.
Host memory에서 커널 M_h 배열이 할당되고 초기화됬다고 가정하면, M_h의 값들은 다음의 API 함수를 통해 디바이스 상수 메모리에 위치한 M에게 전달할 수 있습니다.
cudaMemcpyToSymbol(M, M_h, Kernel_Width * sizeof(float));일반적으로 cudaMemcpyToSymbol 함수는 다음과 같이 사용됩니다. dest는 상수 메모리의 위치에 대한 포인터이고, src는 Host 메모리에 있는 데이터에 대한 포인터, size는 복사할 바이트의 수 입니다.

커널 함수는 상수 메모리 변수를 전역 변수로 액세스합니다. 따라서, 이들의 포인터는 파라미터로 전달될 필요가 없습니다. 상수 메모리를 사용하도록 코드를 수정하면, 다음과 같습니다. 유일한 차이점은 M이 더이상 매개변수로 전달될 필요가 없다는 것입니다.
__global__ void convolution1D_basic(float* N, float* P, int Kernel_Width, int Width)
{
int i = blockIdx.x*blockDim.x + threadIdx.x;
float Pvalue = 0.f;
int N_start_point = i - (Kernel_Width/2);
for (int j = 0; j < Kernel_Width; j++) {
if (N_start_point + j >= 0 && N_start_point + j < Width)
Pvalue += N[N_start_point + j] * M[j];
}
if (i < Width)
P[i] = Pvalue;
}이 코드는 Host 코드에 의해 선언된 전역 변수로 액세스됩니다. 여기에는 전역 변수에 대한 C 언어 범위 규칙이 적용되기 때문에 만약 Host 코드와 커널 코드가 서로 다른 파일에 위치하는 경우, 커널 코드 파일은 M의 선언이 커널에서 확인될 수 있도록 external 선언이 커널 코드에 필요합니다.
전역 메모리 변수와 마찬가지로 상수 메모리 변수로 DRAM에 위치합니다. 그러나 CUDA 런타임은 커널 실행 중에 상수 메모리 변수가 변경되지 않는다는 것을 알고 있기 때문에 커널 실행 중에 하드웨어가 상수 메모리 변수를 공격적으로 캐시하도록 합니다.
상수 메모리 사용의 장점을 이해하려면, 먼저 프로세서 메모리와 캐시 계층에 대해서 알아야하는데, 사실 저도 겉핧기로만 이해하고 있습니다.. ㅠ
이전의 CUDA 메모리 관련 포스팅에서 DRAM의 긴 latency와 제한된 대역폭은 거의 모든 프로세서에서 주요 병목 현상 원인입니다. 이 메모리 병목 현상을 줄이기 위해 요즘 프로세서는 일반적으로 on-chip 캐시 메모리, 즉, 캐시를 사용하여 아래 그림처럼 메인 메모리(DRAM)에서 액세스해야 하는 변수의 수를 줄입니다.
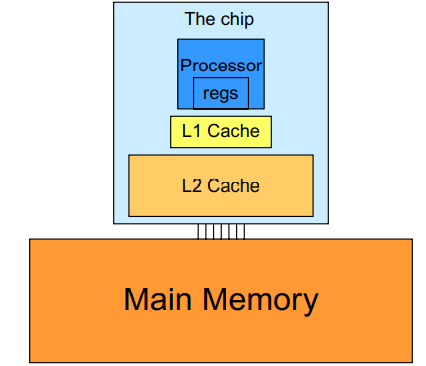
CUDA에서 공유 메모리를 사용하기 위해서는 프로그램에서 변수를 __shared__ 키워드로 선언하고 전역 메모리 변수의 값을 공유 메모리 변수로 명시적으로 이동해주어야 합니다. 반면에 캐시를 사용할 때는 단순히 원래 변수에 접근하면 됩니다. 프로세서 하드웨어는 자동으로 가장 최근에 사용되거나 자주 사용되는 변수의 일부를 캐시에 보관하고 원래의 DRAM 주소를 기억합니다. 나중에 기억하고 있는 변수 중 하나를 사용하면 하드웨어가 주소에서 변수의 복사본이 캐시에서 사용 가능하다는 것을 감지합니다. 그러면 변수의 값이 캐시에서 제공되기 때문에 DRAM에 액세스할 필요가 없어집니다.
메모리 사이즈와 속도 사이에는 tradeoff가 있습니다. 이로 인해 현대 프로세서는 여러 레벨의 캐시를 사용하는데, 캐시 레벨은 프로세서까지의 거리를 반영합니다. 가장 낮은 수준인 Level 1, L1 캐시는 프로세서 코어에 직접 연결된 캐시입니다. latency나 대역폭이 프로세서에 가까운 속도로 수행됩니다. 그러나 L1 캐시의 크기는 일반적으로 16KB에서 64KB로 작습니다. L2 캐시는 128KB에서 1MB의 범위를 가지지만, 액세스하는데 수십 사이클의 클럭이 걸릴 수 있습니다.
디바이스에서 L1 캐시나 L2 캐시는 일반적으로 여러 프로세서 코어나 SMs 간에 공유됩니다.
(일부 최신 디바이스에서는 수 MB의 크기를 가진 L3 캐시도 있습니다.)
병렬 프로그램에서 캐시를 사용할 때 주요 문제점은 캐시 일관성(cache coherence)인데, 하나 이상의 프로세서 코어가 캐시 데이터를 수정할 때 발생합니다. 따라서 대규모 병렬 프로세서에서 캐시 일관성은 지원하기 어렵고 비용이 큽니다.
현대 GPU는 두 레벨의 캐시를 지원하는데, 이 캐시는 일반적으로 캐시 일관성없이 프로세서의 산술 처리량을 증가시키는데 필요한 하드웨어 리소스를 극대화합니다.
상수 메모리 변수는 대규모 병렬 프로세서에서 캐시를 사용하는데 중요한 역할을 합니다. 커널 실행 중에 변경되지 않기 때문에 캐시 일관성 문제가 발생하지 않습니다. 따라서 하드웨어는 L1 캐시에 상수 변수의 값들을 적극적으로 캐싱할 수 있습니다. 게다가 이런 프로세서의 캐시 디자인은 일반적으로 많은 수의 스레드에 값을 broadcast할 수 있도록 최적화되어 있습니다. 그 결과, 워프 내의 모든 스레드들이 M과 같은 상수 메모리 변수에 액세스할 때, 캐시는 엄청난 양의 대역폭을 제공할 수 있습니다. 또한, 일반적으로 M의 크기는 작기 때문에 모든 M의 원소들이 항상 캐시로부터 효과적으로 액세스할 수 있다고 가정할 수 있습니다. 따라서 M을 액세스하기 위해 DRAM의 대역폭은 사용되지 않는다고 볼 수 있습니다. 이렇게 상수 메모리와 캐싱을 사용하면, 메모리 액세스에 대한 부동 소수점 산술의 비율을 2.0으로 두배나 증가시킬 수 있습니다.
Tiled 1D Convolution with Halo Cells
이제 컨볼루션 알고리즘에 타일링(Tiling)을 적용하여 N 배열 원소에 액세스할 때 발생하는 메모리 대역폭 이슈를 다루어보겠습니다. 타일 알고리즘에서 스레드들은 협업하여 input 원소를 on-chip 메모리에 로드합니다.
아래 이미지는 4개의 스레드를 가진 블록을 사용하여 16개의 원소의 1D 컨볼루션을 보여주고 있습니다.

여기서는 4개의 output 타일이 있는데, 첫 번째 타일은 N[0]에서 N[3]까지 커버하고, 두 번째는 N[4]에서 N[7], 이런식으로 각 출력 원소를 커버합니다. 여기서 예시를 위해서 블록당 4개의 스레드라고 가정했지만, 실제로는 32개 이상의 스레드를 권장합니다.
타일링 기법에서 첫 번째는 스레드 블록에서의 output 원소들을 계산하는데 필요한 모든 input 데이터를 공유 메모리로 로드해야 합니다. 공유 메모리로 전달할 input 원소의 개수는 컨볼루션 커널의 크기에 따라 달라집니다. 만약 컨볼루션 커널의 크기가 홀수인 2*n+1 이라고 가정하면 P[i]는 input 원소 N[i-n], ..., N[i-1], N[i], N[i+1], ..., N[i+n] 원소들의 가중합으로 계산됩니다. 위 그림의 예시처럼 Kernel_Width가 5라면, n의 값은 2가 됩니다.
따라서, 위 예시에서 블록 0의 스레드들은 P[0]에서 P[3]의 원소들을 계산하기 때문에 여기서 필요한 input 원소는 N[0]에서 N[5]입니다. N[0] 왼쪽에 존재하는 두 개의 ghost cells도 필요한데, 이 ghost cell의 기본값은 0으로 가정합니다.
블록 1의 스레드들은 P[4]에서 P[7]까지의 원소들을 계산하고, N[2]에서 N[9]까지의 input 데이터 원소가 필요합니다.
나머지 블록도 이런식으로 필요한 입력 데이터 원소를 계산할 수 있습니다.
여기서 N[2]와 N[3]은 두 개의 타일에 각각 속하는 것을 볼 수 있습니다. 따라서 이 값들은 공유 메모리에 두 번 로드됩니다. 각 블록의 공유 메모리는 각 블록의 스레드들에서만 액세스할 수 있으므로, 이러한 원소들은 관련된 모든 스레드가 액세스할 수 있도록 각각의 공유 메모리에 로드되어야 합니다.
이렇게 여러 타일에 포함되어 공유 메모리에 로드되는 원소들을 halo cells (skirt cells)이라고 합니다.
다음 코드는 input 데이터를 공유 메모리에 로드하는 커널 함수입니다.
__global__ void convolution1D_tiled(float* N, float* P, int Kernel_Width, int Width)
{
int i = blockIdx.x*blockDim.x + threadIdx.x;
__shared__ float N_ds[TILE_SIZE + MAX_KERNEL_WIDTH - 1];
int n = Kernel_Width / 2;
int halo_index_left = (blockIdx.x - 1)*blockDim.x + threadIdx.x;
if (threadIdx.x >= blockDim.x - n)
N_ds[threadIdx.x - (blockDim.x - n)] = (halo_index_left < 0) ? 0 : N[halo_index_left];
N_ds[n + threadIdx.x] = N[i];
int halo_index_right = (blockIdx.x + 1)*blockDim.x + threadIdx.x;
if (threadIdx.x < n)
N_ds[n + blockDim.x + threadIdx.x] = (halo_index_right >= Width) ? 0 : N[halo_index_right];
__syncthreads();
float Pvalue = 0;
for (int j = 0; j < Kernel_Width; j++)
Pvalue += N_ds[threadIdx.x + j]*M[j];
P[i] = Pvalue;
}먼저 각 블록에 공유 메모리 배열 N_ds를 선언합니다. 공유 메모리 배열의 크기는 halo(ghost) cells들을 모두 포함할 수 있어야 합니다. Kernel_Width가 홀수라고 가정하고, Kernel_Width의 최대값을 MAX_KERNEL_WIDTH라고 한다면, 공유 메모리 배열이 가져야되는 최대 크기는 TILE_SIZE + MAX_KERNEL_WIDTH - 1이 됩니다. (line 4)
다음으로는 타일의 왼쪽 n개의 값들을 공유 메모리에 적재해야합니다.
여기서 n = Kernel_Width / 2 입니다(line 5).
line 7-9는 왼쪽 n개의 input 원소를 공유 메모리에 적재하는 과정을 보여줍니다. 먼저 이전 타일의 원소 인덱스에 스레드 인덱스(halo_index_left)를 매칭시켜줍니다. 그리고 현재 블록의 마지막 n개의 스레드에서 이전 타일의 마지막 n개의 원소들을 공유 메모리에 적재시켜줍니다.

위 이미지에서 4,5,6,7 스레드에서 6,7 스레드가 위 과정을 통해 2,3에 해당하는 원소를 공유메모리에 적재하는 것이죠.
다음 line 11에서는 4,5,6,7에 해당되는 원소를 그대로 공유 메모리에 적재합니다. halo(ghost) cells에 의해서 이 값이 적재되는 공유 메모리의 위치는 n + threadIdx.x 가 됩니다.
그 다음 line 13-15에서는 타일의 오른쪽 n개의 값들을 공유 메모리에 적재합니다. 왼쪽 n개의 값들을 적재할 때와 동일하게, 이번에는 4,5 스레드가 8,9에 해당하는 원소를 공유 메모리에 적재합니다.
이렇게 모든 input 타일의 원소들이 공유 메모리에 적재된 후에는 for-루프를 통해 P 원소의 값을 각 스레드에서 계산합니다(line 19-22). for-루프를 시작하기 전에 __syncthreads() API 함수를 통해 공유 메모리에 적재가 완료된 후에 루프가 시작될 수 있도록 해주는 것을 잊으시면 안됩니다.
1D 컨볼루션에 타일링을 적용한 코드는 생각보다 복잡한데, N 원소들에 대한 DRAM 액세스 수를 줄이기 위해 더 복잡해졌습니다. 그렇다면 타일링을 적용하면 각 스레드 블록에서의 DRAM 액세스 횟수가 어떻게 개선되었는지 살펴보겠습니다.
타일링을 적용하지 않은 1D 컨볼루션에서는 두 가지 케이스가 존재합니다.
Ghost Cells이 없는 스레드 블록의 경우, 각 스레드가 액세스하는 N 원소의 수는 Kernel_Width개입니다. 따라서 각 스레드 블록이 액세스하는 N 원소의 총 수는 blockDim.x * Kernel_Width 또는 blockDim.x * (2n+1) 입니다. 예를 들어, Kernel_Width가 5이고, 각 블록의 스레드 수가 1024개라면, 각 블록의 N 원소 액세스 횟수는 5120번 입니다.
하지만 첫 번째 블록과 마지막 블록에서 Ghost Cells이 포함된 스레드는 ghost cell에 대한 메모리 액세스를 수행하지 않습니다. 따라서 메모리 액세스는 줄어드는데, 각각의 ghost cell을 사용하는 스레드 수를 계산하여 줄어든 메모리 액세스 수를 계산할 수 있습니다. 아래 이미지는 ghost cell을 사용하지 않는 스레드를 보여주는 간단한 예시입니다.

위 이미지에서 가장 왼쪽의 ghost cell은 하나의 스레드에 의해서 사용됩니다. 일반적으로 ghost cell의 개수는 n개이고, 이러한 ghost cell을 사용하는 스레드의 수는 왼쪽에서 오른쪽으로 가면서 1, 2, ..., n개가 됩니다. 따라서, 왼쪽의 ghost cell에 의해서 수행되지 않는 메모리 액세스의 수는 \(\frac{n(n+1)}{2}\)가 됩니다. 위 이미지 예시에서 왼쪽에 있는 ghost cell에 의해 수행되지 않는 메모리 액세스 수는 총 3개가 됩니다.
오른쪽에 있는 ghost cell도 동일한 방식으로 계산되고, 왼쪽 오른쪽을 모두 포함한 ghost cell에 의해 수행되지 않는 메모리 액세스 횟수는 n(n+1)입니다.
스레드 블록이 클수록 작은 컨볼루션 커널 크기의 ghost cell에 의한 영향은 미미할 것으로 추측됩니다.
타일 커널에서 각 N 원소들은 하나의 스레드에 의해서 로드되는데, ghost cell이 없는 블록에서는 왼쪽에서 n개, 오른쪽에서 n개, 총 2n개의 halo cell도 로드됩니다. 따라서 내부에 있는 스레드 블록에서는 blockDim.x + 2n개의 원소가 로드되고, 경계에 위치하는 스레드 블록에서는 blockDim.x + n개의 원소가 로드됩니다.
따라서 내부 스레드 블록의 경우 Basic 1D 컨볼루션 커널과 Tiled 1D 컨볼루션 커널의 메모리 액세스 비율은 다음과 같습니다.
(blockDim.x*(2n+1)) / (blockDim.x + 2n)
경계에 위치하는 블록의 비율은 다음과 같습니다.
(blockDim.x*(2n+1) - n(n+1)/2) / (blockDim.x + n)
대부분의 경우 blockDim.x의 값이 n보다 훨씬 크기 때문에, 두 비율은 n(n+1)/2와 n 항을 무시하여 근사될 수 있습니다.
(blockDim.x * (2n+1)) / blockDim.x = 2n+1 = Kernel_Width
즉, 메모리 액세스 감소 비율은 컨볼루션 커널의 크기에 비례합니다.
두 코드를 실제로 실행시켜서 수행 시간과 성능을 측정해봤습니다.
코드는 아래 링크를 참조하시면 됩니다!
https://github.com/junstar92/parallel_programming_study/blob/master/CUDA/convolution1D/conv1D.cu
GitHub - junstar92/parallel_programming_study: Study parallel programming - CUDA, OpenMP, MPI, Pthread
Study parallel programming - CUDA, OpenMP, MPI, Pthread - GitHub - junstar92/parallel_programming_study: Study parallel programming - CUDA, OpenMP, MPI, Pthread
github.com
먼저 타일링을 적용하지 않고, 상수 메모리만 사용한 1D 컨볼루션 실행 결과입니다.

다음은 타일링을 적용한 1D 컨볼루션 실행 결과입니다.

성능이 조금 더 높게 나오긴 했지만, 여러번 실행시켜봤을 때 성능이 더 안 좋은 경우도 발생했습니다. 특히, 커널 크기에 비례해서 메모리 액세스 비율이 감소하는 것으로 알고 있지만, 실제 성능은 그만큼 향상되지 않는 모습을 보여주고 있습니다.
사실 결과를 봤을 때 많이 의아했고, 아직 이런 결과가 나오는 원인은 잘 모르겠습니다... ㅠ
심지어 상수 메모리를 사용하지 않은 1D 컨볼루션의 경우에도 위 두 종류의 커널 함수와 비슷한 성능을 보여주고 있습니다.... ㅠ
혹시 원인을 아신다면 댓글 부탁드립니다 ㅠ.ㅠ
Simpler Tiled 1D Convolution - General Caching
위의 타일이 적용된 1D 컨볼루션의 코드에서 복잡한 부분은 좌우 halo cell을 공유 메모리에 로드하는 것과 관련이 있습니다. Fermi와 같은 GPU는 general L1, L2 캐시를 제공하는데, L1은 각 SM에 private하지만, L2는 모든 SM 간에 공유됩니다. 따라서, 모든 블록이 L2캐시를 사용하여 공유된 halo cell을 사용할 수 있도록 할 수 있습니다.
블록의 halo cells은 이웃한 블록의 내부 cells입니다. 예를 들어, 아래 그림의 타일 1의 halo cell N[2]와 N[3]은 타일 0의 내부 원소입니다. 블록 1에서 이러한 halo cell을 사용해야할 때, 블록 0에 의한 액세스로 인해 이미 N[2]와 N[3]가 L2 캐시에 있을 가능성이 높습니다.

그래서 이러한 halo cell에 대한 메모리 접근은 추가적인 DRAM 트래픽을 유발하지 않고 자연스럽게 L2 캐시로 전달될 수 있고, 이러한 halo cells에 대한 액세스를 공유 메모리에 로드하여 액세스하는 것이 아니라 원래의 N 배열에 남겨두어서 사용할 수 있습니다.
따라서 더욱 간단하게 아래처럼 커널 함수를 작성할 수 있습니다.
template<unsigned int TILE_SIZE>
__global__
void convolution1D_tiled_L2(float* d_N, float* d_P, int Kernel_Width, int Width)
{
int i = blockIdx.x*blockDim.x + threadIdx.x;
__shared__ float d_Nds[TILE_SIZE];
d_Nds[threadIdx.x] = d_N[i];
__syncthreads();
int this_tile_start_point = blockIdx.x * blockDim.x;
int next_tile_start_point = (blockIdx.x + 1) * blockDim.x;
int N_start_point = i - (Kernel_Width/2);
float Pvalue = 0;
for (int j = 0; j < Kernel_Width; j++) {
int N_index = N_start_point + j;
if (N_index >= 0 && N_index < Width) {
if ((N_index >= this_tile_start_point) && (N_index < next_tile_start_point)) {
Pvalue += d_Nds[threadIdx.x + j - (Kernel_Width/2)]*M[j];
}
else {
Pvalue += d_N[N_index] * M[j];
}
}
}
d_P[i] = Pvalue;
}인접 블록의 n개의 원소에 대해서 이제 공유 메모리가 아닌 전역 메모리에 존재하는 d_N 배열로 액세스합니다. 하지만 이 값은 L2 캐시에 존재할 확률이 높기 때문에 큰 성능의 저하는 발생하지 않습니다.
실제로 이 코드를 실행해보면,

위에서 다른 커널의 성능과 유사한 것을 확인할 수 있습니다.
'NVIDIA > CUDA' 카테고리의 다른 글
| Parallel Prefix Sum (1) (0) | 2021.12.15 |
|---|---|
| Tiled 2D Convolution (0) | 2021.12.14 |
| 부동소수점 (Floating-Point) (0) | 2021.12.11 |
| 리소스 동적 분할 및 제한 사항 (+ device query) (2) | 2021.12.10 |
| Divergent Wraps (예제 : Sum Reduction) (0) | 2021.12.09 |




댓글