References
- Programming Massively Parallel Processors
- https://developer.download.nvidia.com/assets/cuda/files/reduction.pdf
Contents
- Warp Partioning
- Divergence Branch (Divergent Warps)
- Sum Reduction ( + 최적화 버전)
지난 포스팅에서 리소스 측면에서 CUDA의 성능을 제한하는 것을 살펴봤습니다. 이번에는 스레드 실행 측면에서 성능을 제한하는 것에 대해서 살펴보도록 하겠습니다.
CUDA 커널을 실행하면 2-level 계층으로 구성된 스레드들의 그리드가 생성됩니다. Top-level에서 그리드는 1,2, or 3차원 배열의 블록으로 구성됩니다. Bottom-level에서는 각 블록들이 1,2, or 3차원 배열의 스레드로 구성됩니다. 한 블록은 서로 다른 블록들의 수행순서와 상관없이 어떤 순서로도 수행될 수 있는데, 이것은 CUDA 병렬 수행에 있어서 어떤 디바이스에서도 transparent scalability를 가능하게 해줍니다. 그렇다면 각 블록 내의 스레드들의 수행 시점은 어떨까요?
개념적으로 한 블록 내의 스레드들도 서로 상관없이 어떤 순서로든 수행될 수 있다고 가정할 수 있습니다. 어떤 알고리즘의 어느 단계에서 다음 단계를 시작하기 전에 모든 스레드들이 현재 단계를 완료했음을 확실히 하고 싶을 때 barrier synchronization을 사용하면 됩니다. 사실 올바른 커널 수행을 위해서는 어떤 스레드들이 다른 스레드들과 동기를 맞추고 수행한다는 것에 의지하면 안되지만, 다양한 하드웨어 비용을 고려해서 CUDA 디바이스들은 여러 개의 스레드들을 한꺼번에 묶어서 수행하고 있습니다. 이러한 구현으로 인해서 특정 종류의 커널 함수 코드에 대해서 성능의 제약이 발생하기도 합니다. 개발자는 이런 종류의 코드를 동일한 기능을 하는 다른 형태로 바꾸어 더 좋은 성능을 얻도록 하는 것이 좋습니다.
Warp Partioning
이전 포스팅에서 관련해서 알아봤었는데, 각 스레드 블록은 워프(warps)로 파티셔닝됩니다.
(CUDA Thread 동기화 및 스케쥴링 / 리소스 할당)
워프의 실행은 SIMD 하드웨어에 의해서 수행됩니다. 이러한 구현은 하드웨어 제조 비용을 줄이고 더 낮은 전력과 메모리 액세스 병합을 가능하게 합니다. 워프의 사이즈는 디바이스마다 다를 수 있는데, 모든 CUDA 디바이스는 유사한 워프 구성을 사용하고 각 워프는 32개의 스레드로 구성되어 있습니다.
스레드 블록들은 스레드 인덱스 기준으로 워프로 분할됩니다. 만약 스레드 블록이 1차원 배열로 구성된다면, 오직 threadIdx.x만 사용되고 분할은 간단합니다. 워프 내 threadIdx.x 값은 연속적으로 증가합니다. 워프 크기가 32라면, 워프 0은 스레드 0부터 31까지이고, 워프 1은 스레드 32부터 63까지가 됩니다. 일반적으로 워프 n은 32*n부터 32(n+1)-1까지의 스레드가 속합니다. 크기가 32의 배수가 아닌 블록이라면 마지막 워프는 스레드 수를 32로 채우기 위해 의미없는 스레드를 추가합니다. 예를 들어, 한 블록이 48개의 스레드로 구성되어 있다면 이는 두 개의 워프로 분할되고 마지막 워프에는 32개의 스레드로 채우기 위해서 16개의 의미없는 스레드를 추가합니다.
2차원 이상의 스레드들로 구성된 블록들은 워프로 파티셔닝되기 전에 row-major order의 1차원으로 변환됩니다. 순서는 더 큰 y와 z 좌표의 행을 나중에 배열하도록 결정됩니다. 즉, 블록이 만약 2차원의 스레드로 구성된다면 threadIdx.y가 1인 모든 스레드들은 threadIdx.y가 0인 스레드들 다음에 배열합니다. threadIdx.y가 2인 스레드들은 threadIdx.y가 1인 스레드들 다음에 배열되는 형식입니다.
아래 이미지는 2차원 블록이 어떻게 1차원으로 배열되는지 보여주고 있습니다. 이전 포스팅을 보셨더라면 아마 익숙하실 겁니다. 행렬을 1차원으로 표현하는 것과 동일합니다.
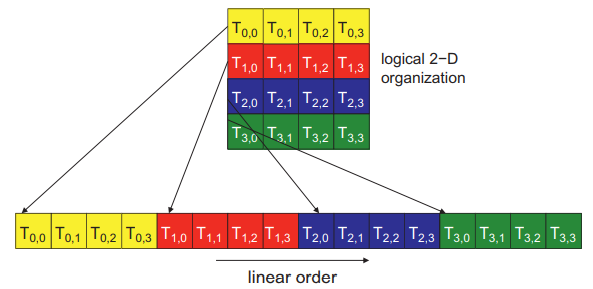
각 스레드는 T\(_{y,x}\)로 표시되는데, x는 그 스레드의 threadIdx.x를 의미하고 y는 threadIdx.y를 의미합니다. 2차원 블록이 1차원으로 표현되는 것을 위 이미지의 아래 그림에서 보여주고 있습니다. 위 그림에서 16개의 스레드는 워프의 반이 됩니다. 나머지 16개의 의미없는 스레드가 추가되어 32개의 스레드로 구성된 하나의 워프가 구성됩니다.
8x8 스레드들로 구성된 2차원 블록이라면, 64개의 스레드는 2개의 워프를 구성할 것입니다. 첫 번째 워프는 T\(_{0,0}\)에서 T\(_{3,7}\)의 스레드로 구성되고, 두 번째 워프는 T\(_{4,0}\)에서 T\(_{7,7}\)의 스레드로 구성될 것입니다.
3차원의 블록이라면 먼저 threadIdx.z가 0인 모든 스레드들을 1차원 순서로 정렬합니다. 그리고 나서 threadIdx.z가 1인 스레드들, 다음은 threadIdx.z가 2인 스레드들, 나머지도 이런식으로 배치됩니다. 4x8x2 블록(x-dim:4, y-dim:8, z-dim:2)이라면 64개의 스레드들이 2개의 워프로 구성될텐데, T\(_{0,0,0}\)에서 T\(_{0,7,3}\) 스레드가 첫 번째 워프에 구성되고, T\(_{1,0,0}\)부터 T\(_{1,7,3}\) 스레드가 두 번째 워프에 구성될 것입니다.
Divergence Branch (분기 브랜치)
SIMD 하드웨어는 워프의 모든 스레드들을 하나의 번들로 실행합니다. 동일한 워프의 모든 스레드들은 하나의 명령을 수행합니다. 이때, 워프가 동일한 실행 경로(제어 흐름 경로,control flow)를 따른다면, 이와 같은 형태의 명령 수행은 더 잘 동작합니다. 예를 들어, if-else 구조가 있을 때, 모든 스레드들이 if 부분을 실행하거나 else 부분을 실행하는 경우에 더 잘 동작한다는 의미입니다. 워프 내의 스레드들이 다른 제어 흐름 경로를 따른다면 SIMD 하드웨어는 분기된 경로들 때문에 여러 단계가 필요해집니다(비효율적이게 됨). 한 단계에서는 if 부분을 따르는 스레드를 실행하고, 그 다음 단계에서는 else 부분을 따르는 스레드를 실행합니다. 이 단계들은 순차적으로 수행되기 때문에 실행 시간이 증가하는 결과를 초래합니다.
조금 더 직관적으로 이해가 되도록 이미지를 하나 가져와봤습니다.
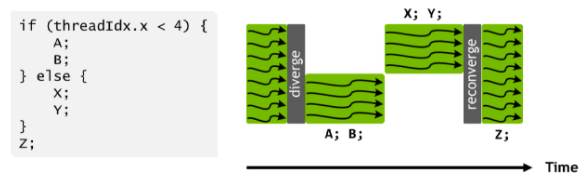
동일한 워프의 스레드들이 다른 실행 경로를 따를 때, 이런 스레드들을 분기(diverge)되었다고 합니다. if-else 예시에서 분기는 워프 내 어떤 스레드들은 if 경로를 따르고, 다른 스레드들은 else 경로를 따릅니다.
분기는 다른 구조에서도 발생하는데, 예를 들어, 워프내 스레드들이 for-루프를 서로 다른 스레드들이 6번, 7번, 8번의 다른 회수만큼 반복하는 경우입니다. 모든 스레드들은 처음 6번의 반복은 모두 함께 수행하고 마칠 것입니다. 그리고 7번째 반복을 위해서는 두 단계가 사용되는데, 한 단계는 반복을 수행하는 스레드들을 위해서 사용되고, 나머지 한 단계는 반복 수행을 하지 않는 스레드들을 위해 사용됩니다. 8번째 반복에서도 반복을 수행하는 스레드를 위한 단계와 그렇지 않은 스레드들을 위한 단계, 총 두 단계가 사용됩니다.
decision condition을 검사하여 스레드의 분기를 발생시키는 지 확인할 수 있는데, decision condition이 threadIdx 값에 근거하고 있는 경우 스레드의 분기를 유발합니다. 예를 들어, if (threadIdx.x 4) {} 라는 구문은 스레드들이 두 개의 분기된 제어 흐름 경로를 따르도록 합니다. 스레드 0, 1, 2, 3이 한 경로를 따르고, 나머지 스레드들이 나머지 경로를 따르게 됩니다. 마찬가지로 루프도 반복 조건이 threadIdx 값에 근거하고 있을 때 스레드 분기를 유발합니다.
스레드 분기 구조를 사용하는 일반적인 이유는 스레드를 데이터에 매핑할 때 경계 조건을 처리하기 위해서 입니다. 일반적으로 총 스레드의 수는 블록 사이즈의 배수가 되지만 데이터의 수는 임의의 수입니다. 아래의 벡터 덧셈 커널에서 line6의 조건이 있는데, 이는 벡터의 길이가 블록 크기의 배수가 아닐 수 있기 때문입니다.
__global__
void vecAddKernel(const float *A, const float *B, float *C, int numElements)
{
int i = blockIdx.x * blockDim.x + threadIdx.x;
if (i < numElements)
C[i] = A[i] + B[i];
}예를 들어, 길이가 1003이고 블록 사이즈 64라면, 총 64*16=1024, 16개의 블록을 실행해야 합니다. 16개의 블록에는 총 1024개의 스레드가 있기 때문에, 마지막 블록의 나머지 21개의 스레드는 허용되지 않는 작업을 하지 않도록 비활성화해야 합니다. 16개의 블록은 32개의 워프로 나누어지는데, 즉, 마지막 워프만 분기 제어를 수행합니다.
처리해야하는 벡터의 크기에 따라 분기 제어에 의한 영향은 감소합니다. 만약 벡터의 크기가 100이라면 4개의 워프 중에 하나는 분기 제어를 가지고 이는 성능에 상당한 영향을 미칠 수 있습니다. 크기가 1000인 경우에는 32개의 워프 중에 1개만 분기 제어를 가지므로 실행 시간의 약 3%에만 영향을 미칩니다. 벡터의 크기가 10000이라면 313개의 워프 중에 1개만 분기 제어가 있으며, 이에 따른 영향은 1% 미만이 됩니다.
2차원의 데이터인 경우에도 비슷합니다. 아래의 76x62 크기의 사진을 처리하기 위해 16x16 스레드로 구성된 20개(5x4)의 2차원 블록을 사용해야합니다. 각 블록은 8개의 워프로 분할되고 각 워프는 블록의 두 행으로 구성됩니다. 여기서는 총 160개의 워프(블록당 8개의 워프)로 분할됩니다.
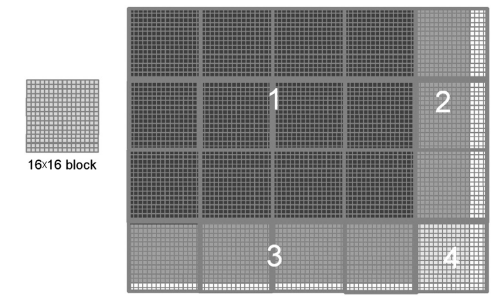
위 이미지에서 1번 영역에 있는 12개의 블록의 워프(96개)에는 분기 제어가 없습니다. 2번 영역에서 24개의 워프는 모두 분기 제어를 가지게 됩니다. 3번 영역의 경우에는 아래쪽에 위치한 워프만 데이터 밖에 매핑됩니다. 즉, 각 블록의 마지막 워프(블록의 15-16행)들은 모두 if 조건을 통과하지 못하므로 분기 제어가 없다고 볼 수 있습니다. 따라서 영역 3에서는 32개의 모든 워프에 분기 제어가 없습니다. 4번 영역에서 처음 7개의 워프만 분기제어가 존재합니다. 마지막 8번째 워프는 3번 영역에서와 마찬가지로 모든 스레드에서 if 조건을 통과하지 못하므로 분기 제어가 없습니다.
따라서, 160개의 워프 중에 31개의 워프만 분기 제어가 있습니다.
이 예제에서도 데이터 크기가 증가함에 따라서 분기 제어에 따른 성능 영향은 감소합니다. 만약 16x16 블록으로 200x150 크기의 사진을 처리한다고 하면, 130개의 블록에서 1040개의 워프가 생성됩니다. 1번 영역에서부터 4번 영역까지의 워프 수는 각각 864, 72, 96, 8개 이며, 이 워프들 중에 80개만이 분기 제어를 가지게 됩니다. 따라서, 분기 제어에 의한 성능의 영향은 8% 미만입니다.
만약 1000픽셀 이상의 사진을 처리한다면 분기 제어가 성능에 영향을 미치는 정도는 2% 미만이 됩니다.
Sum Reduction
분기 제어는 연산에 참여하는 스레드의 수가 시간에 따라 변화하는 일부 병렬 알고리즘에서 자연적으로 발생합니다. 이러한 동작을 확인하기 위해서 Reduction 알고리즘, 그 중에서도 Sum Reduction을 예제로 살펴보겠습니다.
Reduction 알고리즘은 배열에서 하나의 값을 추출하는데, 이 값은 모든 원소의 합, 최대값 또는 최소값 등이 될 수 있습니다. 이런 모든 종류의 Reduction은 동일한 계산 구조를 공유하여 모든 배열의 원소를 순차적으로 방문하면서 손쉽게 얻을 수 있습니다.
아래 코드는 Sum Reduction을 병렬로 수행하는 커널 함수입니다. 다양한 타입의 데이터를 허용하기 위해 template을 사용했습니다. 여기서 ShareMemory는 template화된 타입의 shared memory 배열을 사용할 때 linker error를 피하기 위해서 사용되는 유틸리티 클래스입니다. 이 클래스는 NVIDIA CUDA Sample 코드를 참조하였습니다.
template<class T>
__global__ void sumReduce1(T* g_in, T* g_out, unsigned int size)
{
T *sdata = SharedMemory<T>();
unsigned int t = threadIdx.x;
unsigned int i = blockIdx.x*blockDim.x + threadIdx.x;
sdata[t] = (i < size) ? g_in[i] : 0;
__syncthreads();
for (unsigned int stride = 1; stride < blockDim.x; stride *= 2) {
if (t % (2*stride) == 0)
sdata[t] += sdata[t+stride];
__syncthreads();
}
if (t == 0)
g_out[blockIdx.x] = sdata[0];
}원래의 배열은 전역 메모리에 존재합니다. 그리고 각 블록은 배열의 각 섹션에 대해 reduction을 수행하는데, 먼저 해당 섹션의 원소들을 공유 메모리에 적재하고 병렬 reduction을 수행합니다. 전역 메모리로부터 공유 메모리로 원소들을 적재하는 부분이 위 코드에서 line 8에 나와있습니다. 이 커널에서 reduction은 제자리(in place)에서 수행되는데, 공유 메모리의 각 원소들이 수행결과인 부분합으로 대체된다는 의미입니다. for-루프의 각 반복은 reduction의 한 라운드를 수행합니다.
line 9와 14의 __syncthreads() 구문은 스레드들이 현재 반복을 시작하기 전에 이전에 얻은 모든 부분합들의 생성이 현재 반복을 수행하기 전에 완료됨을 보장합니다. 첫 번째 라운드 이후에 짝수 원소들이 첫 번째 라운드에서 생성된 부분합으로 대체됩니다. 두 번째 라운드 이후에는 인덱스가 4의 배수인 원소에 그 라운드에서 생성된 부분합으로 대체됩니다. 최종 라운드를 마치면, 전체 배열의 총합이 원소 위치 0에 저장될 것입니다.

위 그림은 커널의 수행 과정을 보여주고 있습니다.
만약 배열의 한 섹션이 512개의 원소가 포함되도록 나누면(즉, 블록의 스레드 수가 512개), 커널 함수는 9번의 반복 후에 이 섹션 전체에 대한 최종 합을 생성할 것입니다. 따라서, 섹션의 크기가 블록의 스레드 개수가 됩니다.
위 sumReduce1 커널은 확실히 분기(line 12)를 가지고 있습니다. 루프의 첫 번째 반복에서는 threadIdx.x의 값이 짝수인 스레드들만 덧셈 연산을 수행할 것입니다. 따라서 덧셈 연산을 수행하는 스레드들을 위한 한 단계가 필요하고, 덧셈 연산을 수행하지 않는 스레드를 위한 단계가 또 필요합니다. 이런 분기는 알고리즘을 조금 수정하면 줄어들 수 있습니다.
아래 코드는 조금 수정된 알고리즘으로 Sum Reduction을 구하는 커널 함수입니다.
template<class T>
__global__ void sumReduce3(T* g_in, T* g_out, unsigned int size)
{
T *sdata = SharedMemory<T>();
unsigned int t = threadIdx.x;
unsigned int i = blockIdx.x*blockDim.x + threadIdx.x;
sdata[t] = (i < size) ? g_in[i] : 0;
__syncthreads();
for (unsigned int stride = blockDim.x/2; stride > 0; stride >>= 1) {
if (t < stride)
sdata[t] += sdata[t+stride];
__syncthreads();
}
if (t == 0)
g_out[blockIdx.x] = sdata[0];
}이 코드에서는 첫 번째 반복에서 이웃한 원소들을 더하는 대신, 섹션 크기의 반만큼 떨어진 원소들끼리 더합니다. stride 변수를 섹션 크기의 반으로 초기화함으로써 이를 수행합니다. 첫 번째 라운드 동안 더해진 모든 쌍들은 서로 구획의 반 크기만큼 떨어진 원소이며, 첫 번째 반복이 끝나면 모든 쌍의 부분합은 공유 메모리 배열의 앞쪽에 위치합니다. 루프는 새로운 반복을 시작하기에 앞서 stride 변수를 2로 나누는데, 새로운 반복은 이전 반복의 섹션 크기의 1/2이 되기 때문입니다.
그러나 여전히 for-루프 안에서 if 구문(line 12)을 가지고 있습니다. 그렇다면 첫 번째 살펴봤던 sumReduce1 커널과 비교하여 성능 차이가 존재할까요?
아래 이미지는 sumReduce3 커널의 수행 과정을 보여줍니다.

만약 512개의 원소가 하나의 섹션이라면 첫 번째 라운드에서 0부터 255까지의 스레드에서 13행의 덧셈 연산을 수행하고, 스레드 256부터 511까지는 수행하지 않습니다. 첫 번째 라운드가 끝나고 나면 부분합은 공유 메모리 배열의 원소 0부터 255사이에 저장됩니다. 워프는 연속된 threadIdx.x 값을 가지는 32개의 스레드로 구성되기 때문에 워프 0부터 7에 속하는 모든 스레드들이 덧셈 연산을 수행하고 워프 8부터 15까지는 덧셈 연산을 수행하지 않습니다. 워프 내의 모든 스레드들은 동일한 경로를 따르기 때문에 스레드 분기는 발생하지 않게 됩니다.
하지만, if문에 의한 분기를 완전히 제거하지는 않습니다. 5번째 라운드부터는 덧셈 연산을 수행하는 스레드의 수가 32개 이하로 떨어지는 것을 확인할 수 있습니다. 즉, 마지막 5번의 반복에서는 16, 8, 4, 2, 1개의 스레드만이 덧셈 연산을 수행합니다. 이 반복 동안에는 코드가 여전히 분기를 가집니다.
위의 Sum Reduction 커널 함수를 실행해볼 수 있는 전체 코드는 아래 링크를 참조하시면 됩니다.
https://github.com/junstar92/parallel_programming_study/tree/master/CUDA/reduction
GitHub - junstar92/parallel_programming_study
Contribute to junstar92/parallel_programming_study development by creating an account on GitHub.
github.com
reductionKernel.cu 코드에 sumReduce1이 첫 번째 소개했던 reduction 커널 함수이고, sumReduce3이 바로 위에서 소개한 수정된 reduction 커널 함수입니다. 두 커널을 실행했을 때, 성능의 차이가 어떠한지 한 번 비교해보겠습니다.
배열의 수는 4,000,000개, 블록당 스레드는 512개로 설정하였고, 배열의 데이터 타입은 float 입니다.
먼저 sumReduce1 커널 함수로 실행한 결과입니다.

그리고 sumReduce3 커널 함수로 실행한 결과입니다.

수행 시간이 약 0.24ms 정도 감소한 것을 확인할 수 있고, 따라서 처리량이 18.6 GB/s에서 25.8 GB/s로 증가했습니다. 드라마틱한 성능의 향상은 아니지만, 분기로 인한 성능 하락을 어느 정도 향상시킨 것 같습니다.
추후에 또 다른 Reduction 최적화 방법에 대해서 알아보도록 하겠습니다.
'NVIDIA > CUDA' 카테고리의 다른 글
| 부동소수점 (Floating-Point) (0) | 2021.12.11 |
|---|---|
| 리소스 동적 분할 및 제한 사항 (+ device query) (2) | 2021.12.10 |
| Global Memory 대역폭(bandwidth) 활용 (2) | 2021.12.08 |
| TILING 최적화 for 메모리 Access (tiled matrix multiplication) (4) | 2021.12.06 |
| CUDA의 메모리 Access와 Type (예제 : matrix multiplication) (1) | 2021.12.05 |




댓글