References
- Programming Massively Parallel Processors
Contents
- Global Memory Bandwidth
- Memory Coalescing Technique (메모리 병합 기법)
지난 포스팅들에서 전역 메모리가 아닌 공유 메모리를 사용하는 Tiling 기법을 사용하여 행렬 곱 연산의 성능을 향상시켜봤습니다. 이렇듯 CUDA에서 제공할 수 있는 메모리들을 잘 사용하면, 더 좋은 성능은 갖는 프로그램을 만들 수 있습니다.
TILING 최적화 for 메모리 Access (tiled matrix multiplication)
TILING 최적화 for 메모리 Access (tiled matrix multiplication)
References Programming Massively Parallel Processors Contents Tiling 기법 Tiled Matrix Multiplication 병렬화의 제한 요소인 메모리 크기 지난 포스팅에서 CUDA의 메모리에 관해서 알아봤습니다. CUDA의 메..
junstar92.tistory.com
병렬 프로그램의 실행 속도는 하드웨어의 리소스 제약에 의존적입니다. 병렬 코드와 하드웨어 리소스 사이의 상호 작용을 관리하는 것은 모든 프로그래밍 모델에서 높은 성능을 달성하는데 중요합니다. 이번 포스팅부터 CUDA 디바이스에서 리소스 제약의 주요 유형과 이들이 어떻게 커널 성능에 영향을 미치는지 알아보도록 하겠습니다.
이번 포스팅의 주 내용은 전역 메모리 대역폭의 성능을 끌어올리는 방법과 메모리 병합이 Tile 알고리즘에서 어떻게 적용되는지 자세히 알아보도록 하겠습니다.
(Tile 알고리즘에 대해서 자세하게 언급하지는 않습니다. 위의 포스팅 참조바랍니다 !)
Global Memory Bandwidth
CUDA 커널 성능에 중요한 영향을 미치는 것 중의 하나는 전역 메모리에 있는 데이터에 액세스하는 것입니다. CUDA 어플리케이션은 대규모 데이터 병렬화를 이용하는데, 짧은 시간 내에 전역 메모리에서 대량의 데이터를 처리하는 경향이 있습니다. 이전 포스팅에서 공유 메모리를 사용한 Tiling 기법으로 각 블록의 스레드에서 전역 메모리의 데이터에 액세스하는 횟수를 줄였습니다. 이번 포스팅에서는 효율적으로 전역 메모리의 데이터를 공유 메모리와 레지스터로 옮길 수 있는 memory coalescing(메모리 병합) 기법에 대해서 논의해보도록 하겠습니다. 메모리 병합 기법은 Tiling 기법과 함께 사용되어 전역 메모리 대역폭을 보다 효과적으로 활용하여 CUDA 디바이스의 더 높은 성능을 이끌어냅니다.
CUDA 디바이스의 전역 메모리는 일반적으로 DRAM으로 구현됩니다. 데이터 비트들은 DRAM 셀에 저장되는데, 이들은 매우 작은 커패시터이고 아주 작은 양의 전하의 존재유무로 0과 1이 결정됩니다. 1을 보관하고 있는 DRAM 셀로부터 데이터를 읽기 위해서는 소형 커패시터가 1로 보이기에 충분한 전하량이 있는지 알아내는 메커니즘을 동작해야합니다. 이는 현대 DRAM에서 약 10 nano 초가 걸립니다. 이는 수 나노초의 클럭 사이클 타임을 가지는 현대 컴퓨터 장치와 비교하면 극명한 대조를 보여줍니다. 이상적인 바이트당 수 나노초의 액세스 시간과 비교했을 때 매우 느리기 때문에 데이터 현대의 DRAM은 처리 속도를 높이기 위해서 병렬 처리를 사용합니다. 매번 어떤 DRAM 위치에 액세스할 때마다, 그 위치가 포함된 연속된 많은 위치들도 함께 액세스됩니다. 각 DRAM 칩에는 수많은 센서가 제공되어 병렬적으로 동작하는데, 각 센서는 이 연속적인 위치들의 비트의 내용물을 감지합니다. 일단 센서들에 의해서 감지가 완료되면, 연속적인 위치에 있는 데이터는 아주 빠른 속도로 프로세서에게 전송될 수 있습니다 (연속된 위치에 액세스하고 전달하는 것을 DRAM bursts라고 합니다). 만약 어플리케이션에서 이 버스트들의 데이터의 사용을 잘 활용한다면 DRAM은 무작위 시퀀스의 위치에 액세스했을 때보다 훨씬 더 높은 속도로 데이터를 전달할 수 있습니다.
현대 DRAM의 버스트 구조를 고려하여 현재 CUDA 디바이스는 프로그래머가 스레드의 메모리 접근을 유리한 패턴으로 구성하여 전역 메모리 액세스 효율을 높일 수 있는 기술을 적용하고 있습니다. 이 기술은 워프(warp)에 있는 스레드가 어떤 시점에서든지 동일한 명령을 실행한다는 점을 이용합니다. 워프 내의 모든 스레드들 load 명령을 수행할 때, 하드웨어는 스레드들이 연속적인 전역 메모리 위치에 액세스하는지 검사합니다. 즉, 가장 유리한 메모리 액세스 패턴은 워프 내의 모든 스레드들이 연속된 전역 메모리 위치에 액세스할 때입니다. 이 경우 하드웨어는 이 액세스들을 묶어서 또는 병합해서(combines or coalesces) 연속된 DRAM 위치에 대한 하나의 통합된 액세스로 만듭니다. 예를 들어, 워프에 load 명령어가 주어졌고, 스레드 0이 전역 메모리 위치 N에 액세스하고, 스레드 1이 N+1, 스레드 2가 N+2, 이런 식으로 액세스한다면, 이러한 액세스들은 DRAM에 액세스할 때 연속된 모든 위치들에 대한 하나의 요청으로 묶여서 처리됩니다. 이렇게 병합된 액세스를 통해서 DRAM은 전역 메모리의 최고 대역폭에 가까운 속도로 데이터를 버스트(burst)로 전송할 수 있습니다.
병합 하드웨어(coalescing hardware)를 효과적으로 사용하는 방법을 조금 더 이해하기 위해서 C 스타일 다차원 배열 원소에 액세스할 때 메모리 주소가 어떻게 형성되는지 알아보겠습니다. C와 CUDA에서는 다차원 배열을 row-major로 선형적인 주소의 메모리에 배치합니다. row-major는 데이터를 배치할 때 행의 구조가 유지된다는 것을 의미합니다. 즉, 행의 모든 인접 요소들이 연속된 위치의 주소 공간에 배치됩니다. 아래 그림은 4x4 행렬로 표현되는 배열이 메모리 주소에 row-major로 배치되는 것을 보여주고 있습니다.

아래 이미지는 메모리 병합 측면에서 CUDA 커널 2D row-major 배열 데이터 접근에 유리한 패턴과 불리한 패턴을 보여주고 있습니다.

아래 코드는 간단한 행렬 곱 커널입니다. 각 스레드는 M 배열의 row와 N 배열의 column에 액세스합니다. 위 그림의 (A)는 M 배열의 데이터 액세스 패턴을 보여주며, 하나의 와프의 스레드들은 인접 행의 값을 읽습니다. 즉, iteration 0(k = 0)에서 와프 내의 스레드들은 0 ~ 31행의 0번째 요소(각 행의 첫번째 요소)들을 읽습니다. iteration 1(k = 1) 동안에는 동일한 스레드들이 0 ~ 31행의 1번째 요소(각 행의 두번째 요소)들을 읽게 됩니다. 어떠한 액세스도 병합되지 않습니다.
__global__ void MatrixMulKernel(float* M, float* N, float* P, int Width) { // Calculate the row index of the P element and M int Row = blockIdx.y*blockDim.y+threadIdx.y; // Calculate the column index of P and N int Col = blockIdx.x*blockDim.x+threadIdx.x; if ((Row < Width) && (Col < Width)) { float Pvalue = 0; // each thread computes one element of the block sub-matrix for (int k = 0; k < Width; ++k) { Pvalue += M[Row*Width+k]*N[k*Width+Col]; } P[Row*Width+Col] = Pvalue; } }
보다 유리한 액세스 패턴이 바로 그림 (B)인데, 각 스레드들은 N 행렬의 하나의 열(column)을 읽습니다. iteration 0(k = 0)에서 워프 내 모든 스레드들은 0 ~ 31열의 첫번째 요소를 읽습니다. 모든 액세스가 병합적입니다.
행렬 요소들이 전역 메모리에 어떻게 위치하고 있는지를 더 자세하게 살펴보도록 하겠습니다. 행렬 곱 커널에서 행렬 N는 아래처럼 각 요소에 액세스합니다.
N[k*Width + Col]k번째 루프에서 k*Width의 값은 모든 스레드에서 동일합니다. 그리고 Col = blockIdx.x*blockDim.x + threadIdx.x 에서, 동일한 블록의 모든 스레드는 동일한 blockIdx.x와 blockDim.x의 값을 가지므로 k*Width + Col은 오직 threadIdx.x에 의해서만 값이 변경됩니다. 인접한 스레드들은 연속적인 threadIdx.x의 값을 가지므로 액세스되는 요소들은 연속된 주소를 가집니다. 예를 들어, 아래 이미지를 살펴봅시다. 4x4 블록을 사용하고 워프의 크기가 4라고 가정하겠습니다.

위 예시에서 블록 내의 모든 스레드의 Width, blockDim.x, blockIdx.x의 값은 각각 4, 4, 0 입니다.
Iteration 0에서 k의 값은 0이고, 이때 N 요소에 액세스하는 각 스레드의 인덱스는
가 됩니다. 즉, 이 스레드 블록에서 N에 액세스하는 인덱스는 단순히 threadIdx.x 입니다. T, T, T, T에 의해서 액세스되는 N 요소는 N[0], N[1], N[2], N[3]입니다. 이것이 위 이미지에서 'Load iteration 0' 박스에 해당됩니다. 이 요소들은 전역 메모리의 연속된 위치에 존재합니다.
하드웨어는 워프 내의 스레드들의 액세스가 전역 메모리의 연속된 위치인지 감지하고, 이 액세스들을 하나의 액세스로 통합합니다. 이렇게 함으로써 DRAM은 데이터를 높은 속도로 전달할 수 있게 됩니다.
다음 iteration에서 k의 값은 1입니다. 이제 각 스레드에서 N에 엑세스하는 인덱스는 다음과 같습니다.
T, T, T, T에 의해서 액세스되는 N 요소는 N[4], N[5], N[6], N[7]입니다. 위 그림의 'Load iteration 1' 박스에 해당되고, 워프 내 스레드의 모든 액세스는 다시 하나의 통합된 엑세스로 합쳐져 DRAM의 대역폭 활용을 향상시킵니다.
아래 그림은 병합되지 못하는 행렬 데이터 액세스 패턴을 보여주고 있습니다.

똑같이 4x4 블록을 사용하고 워프의 크기가 4라고 가정해보겠습니다. 이전 예시와 마찬가지로 블록 내 모든 스레드의 Width, blockDim.y, blockIdx.y의 값은 각각 4, 4, 0 입니다. Iteration 0일 때, k의 값은 0이고 각 스레드가 액세스하는 M의 인덱스는 다음과 같습니다.
즉, 액세스되는 M의 인덱스는 threadIdx.y * 4입니다. T, T, T, T에 의해서 액세스되는 M 요소는 M[0], M[4], M[8], M[12]입니다. 이 내용이 위 그림의 'Load iteration 0' 박스에 해당되며, 액세스되는 요소들은 전역 메모리의 연속되어 위치하지 않습니다. 따라서 하드웨어는 이 액세스들을 하나의 액세스로 통합하지 못합니다.
다음 iteration에서 k의 값은 1이고, 각 스레드가 액세스하는 M의 인덱스는 다음과 같습니다.
T, T, T, T에 의해서 액세스되는 M 요소는 M[1], M[5], M[9], M[13]입니다. M 요소의 액세스들은 여전히 하나의 액세스로 통합될 수 없습니다.
결과적으로 커널의 루프가 행 단위로 요소들을 반복한다면, 전역 메모리의 접근이 커널 루프가 열 단위로 요소들을 반복하는 경우보다 훨씬 더 비효율적입니다.
Corner Turning (with Tiling)
만약 알고리즘이 커널 코드를 행 단위로 데이터를 반복한다면 공유 메모리를 사용하여 메모리 병합을 가능하게 할 수 있습니다. 이 기법을 corner turning이라고 하는데, 아래 그림의 행렬 곱 이미지를 살펴보겠습니다.
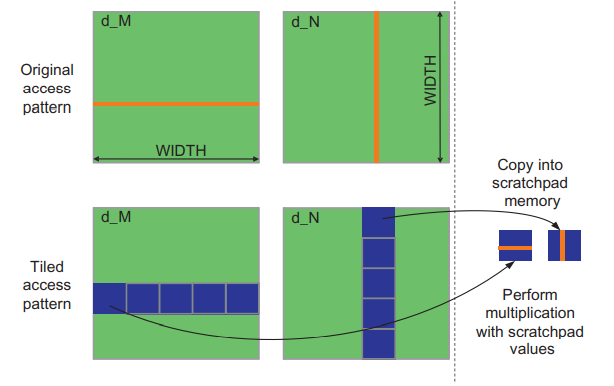
M의 행을 읽는 각 스레드에서의 패턴은 병합될 수 없습니다. 그래도 이전 포스팅에서의 Tile 알고리즘을 통해서 병합을 활성화 할 수 있었습니다. (TILING 최적화 for 메모리 Access (tiled matrix multiplication))
Tile 알고리즘에서 블록 내의 스레드들은 먼저 공유 메모리로 메모리 값들을 읽어들이는데, 이때 병합된 패턴으로 읽어들이도록 주의해야 합니다. 공유 메모리는 매우 빠른 on-chip 메모리이므로 공유 메모리에 데이터가 저장되면, 높은 데이터 액세스 속도를 달성하기 위해서 병합할 필요없이 열 기반이나 행 기반에 상관없이 액세스할 수 있습니다.
아래의 코드는 Tile 알고리즘을 사용한 행렬 곱셈 커널입니다. 행렬 M과 N의 타일을 공유 메모리에 적재하여 연산에 사용합니다.
__global__ void MatrixMulKernel(float* M, float* N, float* P, int Width) { __shared__ float Mds[TILE_WIDTH][TILE_WIDTH]; __shared__ float Nds[TILE_WIDTH][TILE_WIDTH]; int bx = blockIdx.x; int by = blockIdx.y; int tx = threadIdx.x; int ty = threadIdx.y; // Identify the row and column of the P element to work on int Row = by * TILE_WIDTH + ty; int Col = bx * TILE_WIDTH + tx; float Pvalue = 0; // Loop over the M and N tiles required to compute the P element for (int ph = 0; ph < Width/TILE_WIDTH; ++ph) { // Collaborative loading of M and N tiles into shared memory Mds[ty][tx] = M[Row*Width + ph*TILE_WIDTH + tx]; Nds[ty][tx] = N[(ph*TILE_WIDTH + ty)*Width + Col]; __ syncthreads(); for (int k = 0; k < TILE_WIDTH; ++k) { Pvalue += Mds[ty][k] * Nds[k][tx]; } __syncthreads(); } P[Row*Width + Col] = Pvalue; }
line 17-18에서 블록의 각 스레드가 루프의 시작 부분에서 M 요소 하나, N 요소 하나를 공유 메모리 Mds와 Nds로 적재하고 있습니다. 스레드들은 각 행렬에서 어떤 요소를 적재할지 경정하기 위해서 threadIdx.y와 threadIdx.x를 사용합니다.
M의 요소들은 line 17에서 적재되는데, 각 스레드의 인덱스 계산에 ph가 사용되어 타일의 왼쪽끝 위치를 계산합니다. 여기서 M의 column 인덱스는 threadIdx.x에 의해서만 달라지고, row 인덱스는 blockIdx.y와 threadIdx.y에 의해 결정됩니다. 이는 동일한 blockIdx.y와 threadIdx.y 값을 가지고 인접한 threadIdx.x의 값을 가지는 스레드들은 인접한 M 요소들에 액세스한다는 것을 의미합니다. 즉, 타일의 각 행은 TILE_WIDTH 개의 스레드에 의해서 적재되고 그 스레드들의 threadIdx는 y 차원에서는 동일하고 x 차원에서 연속적이기 때문에 하드웨어는 이를 하나의 병합된 액세스로 묶어서 처리합니다.
N의 경우에는 row 인덱스 ph*TILE_WIDTH + ty의 값은 같은 threadIdx.y 값을 갖는 스레드에서 모두 동일합니다. 여기서 의문은 인접한 threadIdx.x 값을 갖는 스레드들이 한 행에서 인접한 N 요소에 액세스하느냐입니다. 각 스레드에서 column 인덱스 계산은 Col = bx*TILE_WIDTH + tx (line 11) 입니다. bx*TILE_WIDTH는 동일한 블럭의 모든 스레드들에서 같습니다. tx는 단순히 threadIdx.x의 값입니다. 따라서, 인접한 threadIdx.x의 값을 갖는 스레드들은 한 행에서 인접한 N 요소에 액세스하고, M과 마찬가지로 하나의 병합된 액세스로 처리합니다.
Tile 알고리즘을 적용하지 않은 행렬 곱셉 커널에서는 인접한 threadIdx.x 값을 갖는 스레드들이 row major 레이아웃에서 물리적으로 인접하지 않은 수직으로 인접한 요소들에 액세스합니다. Tile 알고리즘은 연속된 threadIdx.x 값을 갖는 스레드들이 수직으로 인접한 요소에 액세스하는 패턴을 수평으로 인접한 요소에 액세스하도록 변환시켜줍니다. 이렇게 수직 액세스 패턴을 수평 액세스 패턴으로 바꿔주는데, 이를 corner turning이라고 합니다. Corner turning는 또한 2D 배열이 column-major order로 배치되는 포트란과 같은 언어에서 유용합니다.
Tile 알고리즘에서 M과 N의 요소들의 load가 병합(coalesced)됩니다. 따라서, Tile 알고리즘은 단순한 행렬 곱셈에 비해서 두 가지 장점이 있습니다. 하나는 공유 메모리의 데이터 재사용 덕분에 메모리 load 횟수가 감소한다는 것입니다. 다른 하나는 메모리 load가 병합되기 때문에 DRAM 대역폭 활용이 더욱 향상됩니다. 이 두 가지 개선사항은 서로의 장점을 극대화시켜주고 커널의 실행 속도를 매우 크게 증가시킬 수 있습니다. 이전 포스팅의 결과를 살펴보면, 약 5~6배의 성능 향상을 이끌어 냈습니다.
Tile 알고리즘 코드의 line 10-11, 17-18은 행렬 요소를 공유 메모리에 적재하기 위해 자주 사용되는 프로그래밍 패턴을 사용했습니다. 그리고 각 단계의 line 20-22 dot-product에서 워프 내의 스레드들이 Mds의 연속적인 위치에 액세스하지 않습니다. 하지만 이는 Mds가 공유 메모리에 위치하기 때문에 문제가 되지 않습니다. 위에서 언급했듯이 공유 메모리에서는 빠른 속도의 데이터 액세스를 위한 병합이 필요없습니다.
'NVIDIA > CUDA' 카테고리의 다른 글
| 리소스 동적 분할 및 제한 사항 (+ device query) (2) | 2021.12.10 |
|---|---|
| Divergent Wraps (예제 : Sum Reduction) (0) | 2021.12.09 |
| TILING 최적화 for 메모리 Access (tiled matrix multiplication) (4) | 2021.12.06 |
| CUDA의 메모리 Access와 Type (예제 : matrix multiplication) (0) | 2021.12.05 |
| CUDA Thread 동기화 및 스케쥴링 / 리소스 할당 (0) | 2021.12.04 |




댓글