CNN
대뇌의 시각 피질 연구에서 시작된 Convolutional Neural Network(합성곱 신경망)은 이미지 인식 분야에 많이 사용됩니다. 이 기술은 이미지 인식뿐만 아니라 음성인식이나 자연어처리(NLP) 같은 다른 분야에서도 많이 사용되고 있습니다.
데이비드 허블과 토르스텐 비셀의 시각 피질 연구를 통해서 시각 피질 안의 많은 뉴런이 작은 local receptive field를 가진다는 것을 보였는데, 쉽게 설명하면 뉴런들은 보고있는 이미지에서 수직선, 대각선 등의 일부 시각 자극에만 반응하고, 뉴런들을 서로 겹쳐서 전체 이미지를 만들어서 인식한다는 것입니다.
즉, 어떤 뉴런은 수평선 이미지에만 반응하고 다른 뉴런은 다른 각도의 선분에 반응한다는 것을 발견한 것이죠.

이러한 시각 피질 연구를 통해서 점진적으로 CNN(합성곱 신경망)이라고 부르는 것으로 발전해왔습니다.
특히 1998년 얀 르쿤 등의 논문이 비전 영역에서 중요한 터닝포인트가 되었고, 이 논문에서 손글씨 숫자를 인식하는데 사용된 LeNet-5 구조를 소개하고 있습니다. 이 구조에는 익숙한 완전 연결층(fully connected layer)와 sigmoid activation function과 같은 요소도 있지만, Convolution layer와 Pooling layer라는 새로운 요소가 소개되고 있습니다.
CNN 구조의 중요한 부분을 차지하는 Convolution layer와 Pooling layer에 대해서 알아보도록 합시다.
Convolution layer 합성곱 층
CNN의 가장 중요한 구성 요소는 Convolution layer(Conv layer)입니다.
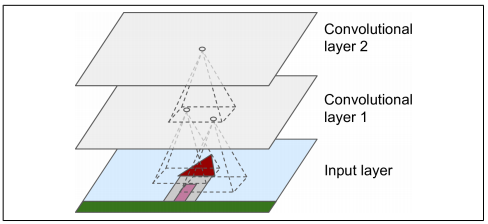
딥러닝의 'Hello world'인 MNIST 분류 예제를 경험해보셨으면 Multi Perceptron layer를 구성해서 입력 픽셀을 한 줄로 길게 펼친 후에 학습을 진행해보셨을겁니다.
하지만, 위 이미지에서 첫 번째 Conv layer의 뉴런(파라미터)은 입력 이미지의 모든 픽셀에 연결되는 것이 아니라 Conv layer의 뉴런의 receptive field 안에 있는 픽셀에만 연결되는 것을 볼 수 있습니다. 그리고 두 번째 Conv layer에 있는 각 뉴런은 첫 번째 layer의 작은 사각 영역 안에 위치한 뉴런들과 연결된 것을 볼 수 있습니다.
이런 구조는 네트워크가 첫 번째 Conv layer에서 low-level의 특성(feature)에 집중하고, 두 번째 Conv layer에서 조금 더 큰 high-level의 특성으로 조합하도록 도와줍니다.
CNN은 이런 계층적인 구조로 이루어져 있으며, 단순히 이미지를 펼쳐서 픽셀을 입력으로 받는 것이 아니라 이미지의 부분적인 특징(feature)들을 읽고 학습하기 때문에 fully-connected layer로 이루어진 네트워크보다 좋은 성능을 보입니다.
Filter 필터
Conv layer의 weight 파라미터는 필터(또는 커널 Kernel)이라고 부르며, Conv layer에서 여러 개의 필터들을 통해 이미지의 특징을 추출하게 됩니다.
예를 들어, 아래와 같은 3x3 필터는 수직선을 검출하는 필터입니다.

이 필터를 가지고 원본 이미지와 convolution 연산을 수행하면, 수직선을 제외한 나머지 특성들을 무시하고 수직선만을 나타내게 됩니다.
여기서 convolution 연산은 필터가 이미지 위를 이동하면서 원소별 곱셈의 적분을 계산하는 수학연산으로 신호처리 분야에서 많이 사용되는 특징 추출(Feature Extraction) 기법입니다.

만약 수평선을 검출하는 필터를 사용한다면, 다음과 같은 이미지를 얻을 수 있습니다.

이렇게 Conv layer에 적용된 하나의 필터는 하나의 특성맵(Feature Map)을 만들게 됩니다. 이 맵은 필터를 가장 크게 활성화시키는 이미지의 영역을 강조하게 되며, 네트워크 모델은 이 특성들을 학습해서 이미지를 분류하게 됩니다.
물론 이러한 필터들은 수작업으로 정의할 필요가 없습니다. Conv layer는 특징을 검출하는 필터를 수작업으로 설계하지 않고, 학습을 통해서 해당 이미지 또는 문제에 가장 유용한 필터를 학습하게 됩니다.

위 이미지 예시에서는 하나의 필터만 적용해서 어떤 특성맵이 추출되는지 확인했는데, 실제 Conv layer에서는 여러 개의 필터를 가지고 각 필터마다 하나의 특성맵을 출력하므로 3D로 표현됩니다. Input layer에서의 입력 이미지는 보통 색을 나타내는 채널(RGB)이 존재할 수 있습니다.
각 특성맵의 픽셀은 하나의 뉴런에 해당하고, 하나의 특성맵 안에서는 모든 뉴런이 같은 파라미터를 공유하며, 만약 다른 특성맵이라면 뉴런은 다른 파라미터를 사용하게 됩니다. 이렇게 하나의 Conv layer에서 여러 필터를 동시에 적용해서 이미지의 여러가지 특성(feature)를 감지할 수 있습니다.
또한, 이렇게 뉴런이 파라미터를 공유함으로써 모델의 전체 파라미터의 수를 급격하게 줄여줍니다.
MNIST 분류 예제의 경우에는 하나의 이미지가 단지 (28x28)의 크기를 갖기 때문에 일반적인 DNN을 사용하더라도 파라미터의 수가 많지 않습니다. 하지만 500x500 크기의 이미지를 입력으로 사용한다면, 파라미터의 수가 급격하게 증가하게 됩니다.
하지만, CNN은 하나의 특성맵에서 파라미터를 공유하기 때문에 이런 문제를 해결할 수 있습니다.
Pooling layer
단순하게 Pooling layer는 이미지를 압축하는 역할을 담당합니다. CNN의 문제점 중의 하나는 많은 양의 RAM을 차지한다는 것인데, 특히 학습 시에 Backpropagation(역전파) 알고리즘이 역방향 계산을 수행할 때, 정방향에서 계산했던 모든 중간 값들을 필요로 하기 때문입니다.
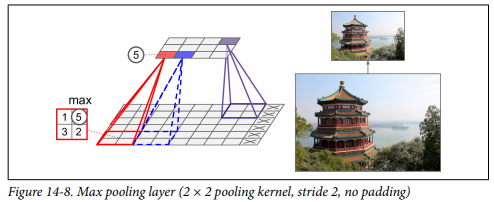
Pooling layer는 계산량 및 메모리 사용량을 줄여줄뿐만 아니라, 과적합(overfitting)을 방지하고 파라미터의 수도 감소시켜 줍니다. 즉, 이미지를 압축해서 축소본(subsampling)을 만들어주는데, 아래 이미지는 Max Pooling layer의 결과를 보여주고 있습니다.
(Max Pooling은 필터 내의 최대값만을 취해서 이미지를 압축하는 방법입니다)
이외에도 Pooling layer는 작은 변화에도 일정 수준의 불변성(invariance)를 만들어줍니다.
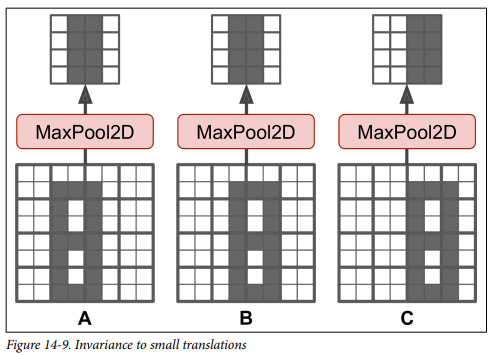
동일한 물체(A, B, C)가 이동하더라도 전체적으로 일정 수준의 이동 불변성을 얻을 수 있습니다. 제한적이긴 하지만, 이와 같은 불변성은 분류 작업의 예측에서 이런 작은 부분이 영향을 받지 않도록 할 수 있습니다.
Max Pooling의 경우에는 단점도 존재하는데, 이미지의 정보를 많이 누락(파괴)시킨다는 것입니다. 이 글에서 설명하지는 않았지만, 2x2 필터와 스트라이드(Stride) 2를 사용하면 출력은 1/4로 줄어들어 입력의 75%를 잃게 됩니다.
Max Pooling 뿐만 아니라 필터 내의 픽셀의 평균을 계산하는 Average Pooling도 있습니다. 일반적으로 Max Pooling이 더 성능이 좋아서 대부분 Max Pooling을 사용하지만, 일반적으로 Average Pooling이 Max Pooling보다 정보 손실이 적습니다.
반면 Max Pooling은 의미 없는 것들은 제거하고 가장 큰 특징만 유지하기 때문에 다음 층에서 조금 더 명확한 신호로 학습할 수 있습니다.(최대값만 취하기 때문에 연산량도 적습니다.)
Conv layer에서 추출한 특성맵을 Max Pooling layer에 통과시키면, 아래와 같은 결과를 얻을 수 있습니다.

크기도 감소되지만, 이미지 비교를 위해서 동일한 크기로 맞추었습니다.
CNN 구조
전형적인 CNN 구조는 Conv layer를 몇 개 쌓고, 그 다음에는 Pooling layer를 쌓는 구조를 반복합니다.

따라서, 네트워크를 통과하여 진행할수록 이미지는 점점 작아지지만, Conv layer 때문에 일반적으로 더 깊어집니다(더 많은 특성맵을 가집니다). 그리고, Top에는 몇 개의 Fully connected layer로 구성된 일반적인 신경망이 추가되고 마지막 layer에서 (sigmoid나 softmax layer를 통해) 예측을 출력합니다.
-참조
Hands On Machine Learning 2nd
'ML & DL > Study' 카테고리의 다른 글
| AutoEncoder (2) : Manifold Learning (1) | 2021.02.10 |
|---|---|
| AutoEncoder (1) : Maximum likelihood 관점에서의 해석 (0) | 2021.02.09 |
| Gradient Descent (0) | 2020.12.16 |
| Activation Function (Feat, non-linearity 비선형) (3) | 2020.12.14 |
| [ML] Support Vector Machine(SVM) (0) | 2020.08.26 |




댓글