Gradient descent
Gradient descent(이하 GD)는 함수 최적화(optimization) 알고리즘의 하나이며, local minimum을 찾기 위해 미분의 개념을 적용한 알고리즘입니다.
자세히 살펴보기 전에 직관적으로 이야기해보자면,
산의 정상을 향해서 오르거나, 깊은 골짜기로 내려가는 경우에 현재 위치에서 경사가 가장 가파른 방향으로 오르거나 내려가다보면 정상(local maximum)에 다다르거나 가장 깊은 골짜기(local minimum)로 내려갈 수 있습니다.
이러한 개념이 바로 Gradient Descent입니다.
(local maximum, 즉 정상을 향해서 진행하는 것은 Gradient ascent라고 합니다.)

- Gradient
gradient는 각 변수의 일차 편미분값으로 구성되는 벡터이며, 다변항에서는 다음과 같이 계산할 수 있습니다.
\[\triangledown F = (\frac{\partial F}{\partial x_1}, \frac{\partial F}{\partial x_2}, \cdots, \frac{\partial F}{\partial x_n})\]
이 벡터는 F의 값이 가장 빠르게 증가하는 방향을 나타내며, F의 크기는 기울기를 나타냅니다. 벡터에 음의 부호를 취해주면, 가장 빠르게 감소하는 방향이 됩니다.
Gradient Descent는 이러한 gradient의 특성을 사용해서 어떤 Cost Function의 값을 최소화시키기 위한 파라미터 값을 찾는 최적화 알고리즘입니다.
- Gradient descent 알고리즘
Gradient Descent의 기본 아이디어는
'어떤 multi-variable 함수 \(F(x)\)가 있고, 그 미분항이 \(\triangledown F\)라고 할 때,
초기값인 어떤 point vector a에서 시작해서 a에서의 \(\triangledown F(a)\)의 반대 반향으로 a를 점진적으로 이동시키면 \(F(x)\)가 최소가 되는 a를 찾을 수 있다.'
라는 것입니다. 즉, 현재 위치에서 함수값이 변화가 가장 큰 방향으로 이동한다는 것입니다.
여기서 함수 \(F(x)\)는 Cost Function이 되겠죠.
파라미터 \(w\)를 가지는 Cost function \(J(w)\)을 예로 들면, 다음과 같이 정의할 수 있습니다.

현재 초기 위치에서의 미분값을 구하고, 그 기울기의 반대방향으로 위치를 업데이트해주면서 점진적으로 local optima로 향하게 됩니다. 만약 local optima에 도달하면, 그 위치에서의 미분값은 0이기 때문에 더 이상 업데이트되지 않습니다.
수렴할 때까지 반복하기 때문에, Gradient Descent는 steepest desecnt라고 불리기도 합니다.

- Learning rate
Gradient Descent에서 Cost Function의 미분항을 구하고 파라미터를 업데이트할 때, 미분값에 가중치인 \(\alpha\)를 적용해서 파라미터를 업데이트하게 됩니다. 이때, \(\alpha\)는 learning rate이며, 알고리즘의 수렴 속도를 조절해주는 역할을 합니다.
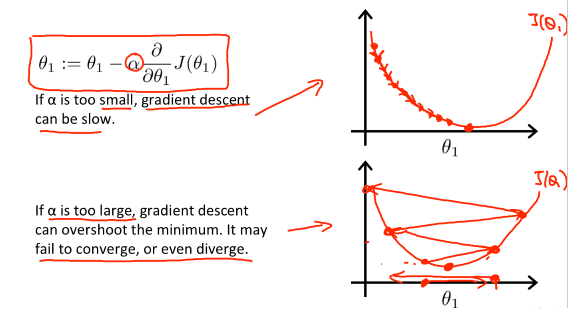
만약 learning rate가 너무 작다면, 천천히 local optima로 향할 것이고, 반대로 너무 크다면 local optima로 수렴하지 못하고, 심지어 발산하는 경우가 발생할 수도 있습니다.
- Gradient Descent의 문제점
Gradient Descent 알고리즘의 문제점은 우리가 구한 최적해가 local minimum에 빠질 수 있다는 것입니다.
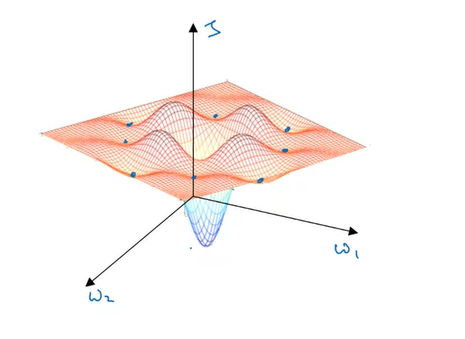
실제 Cost Function이 위와 같은 그래프를 가질 때, 초기 위치에 따라서 global minimum(목표지점)이 아닌 local minimum으로 수렴하게 될 수 있는 것이죠.
딥러닝 초기에는 위와 같은 그래프를 예로 들면서, local optima이 쉽게 발생할 수 있다고 추측했지만, 위 그래프는 올바르지 않은 그래프이며, 기울기가 0인 지점은 대부분 saddle point입니다.

또한, 파라미터의 수가 매우 많은 요즘 트렌드에서 모든 파라미터가 local optima에 빠져야 local optima로 수렴하기 때문에, Convex function인지 확인이 되지 않더라도 local optima에 빠질 확률이 거의 없다라고 봅니다.
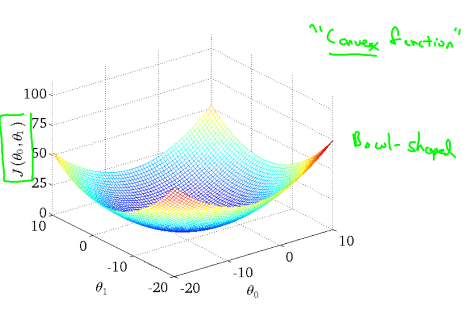
그래도 혹시 모를 local optima에 빠지지 않기 위해서는 Cost Function이 Convex function이 되도록 하는 것이 중요한데, Convex function은 항상 bowl-shape가 되어 항상 global optima로 수렴하게 되어있습니다.
또 다른 문제점으로는 plateaus 문제가 있습니다.
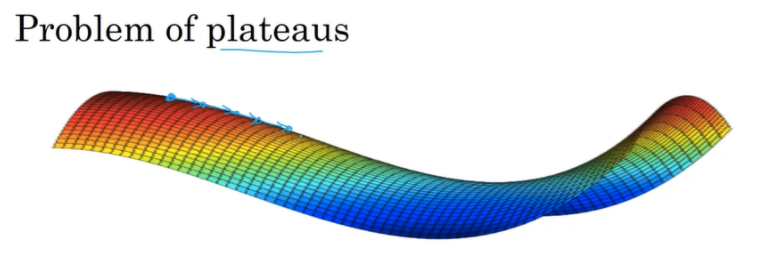
위 문제는 기울기가 0이거나 0에 근접하기 때문에 그래프가 매우 완만해서 해당 구간을 빠져나오는데 굉장이 많은 시간이 소요되거나 심지어 불가능할 수 있습니다.
이 문제는 momentum, RMSprop, Adam과 같은 최적화 알고리즘을 통해서 해결할 수 있습니다.
위 최적화 알고리즘에 궁금하시면 아래 게시글을 참조하시기 바랍니다.
2020/10/02 - [Coursera 강의/Deep Learning] - Optimization(최적화 알고리즘) : Mini-batch/Momentum/RMSprop/Adam
참고
'ML & DL > Study' 카테고리의 다른 글
| AutoEncoder (2) : Manifold Learning (1) | 2021.02.10 |
|---|---|
| AutoEncoder (1) : Maximum likelihood 관점에서의 해석 (0) | 2021.02.09 |
| Convolutional Neural Network(CNN) (0) | 2021.01.04 |
| Activation Function (Feat, non-linearity 비선형) (3) | 2020.12.14 |
| [ML] Support Vector Machine(SVM) (0) | 2020.08.26 |




댓글