해당 내용은 Coursera의 딥러닝 특화과정(Deep Learning Specialization)의 두 번째 강의 Improving Deep Neural Networks: Hyperparameter tuning, Regularization and Optimization를 듣고 정리한 내용입니다. (Week 2)
2주차는 학습 알고리즘을 더 빠르게 학습시킬 수 있는 최적화 알고리즘에 대해서 실습을 진행할 예정입니다.
좋은 최적화 알고리즘은 좋은 결과를 얻기 위해서 몇 일이 걸리는 작업을 몇 시간으로 줄일 정도로 유용한 알고리즘입니다.
우선 이번 실습에 사용되는 패키지입니다.
import numpy as np
import matplotlib.pyplot as plt
import scipy.io
import math
import sklearn
import sklearn.datasets
from opt_utils_v1a import load_params_and_grads, initialize_parameters, forward_propagation, backward_propagation
from opt_utils_v1a import compute_cost, predict, predict_dec, plot_decision_boundary, load_dataset
from testCases import *
%matplotlib inline
plt.rcParams['figure.figsize'] = (7.0, 4.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'
1. Gradient Descent
우선 간단히 머신러닝에서 일반적으로 사용되는 Gradient Descent(GD)를 살펴보겠습니다. 각 step에서 모든 sample m에 대해서 gradient steps을 진행하는데, 이것은 Batch Gradient Descent라고도 불립니다.
Gradient Descent update rule은 다음과 같습니다.
for \(l = 1, ..., L\)
\[\begin{matrix} W^{[l]} = W^{[l]} - \alpha dW^{[l]} \\ b^{[l]} = b^{[l]} - \alpha db^{[l]} \end{matrix}\]
여기서 L은 layer의 수이며, \(alpha\)는 learning rate입니다. 모든 파라미터는 parameters 딕셔너리 변수에 저장되고, for문에서 l은 0부터 시작하기 때문에 l+1로 shift해야하는 것에 주의해야합니다.
# GRADED FUNCTION: update_parameters_with_gd
def update_parameters_with_gd(parameters, grads, learning_rate):
"""
Update parameters using one step of gradient descent
Arguments:
parameters -- python dictionary containing your parameters to be updated:
parameters['W' + str(l)] = Wl
parameters['b' + str(l)] = bl
grads -- python dictionary containing your gradients to update each parameters:
grads['dW' + str(l)] = dWl
grads['db' + str(l)] = dbl
learning_rate -- the learning rate, scalar.
Returns:
parameters -- python dictionary containing your updated parameters
"""
L = len(parameters) // 2 # number of layers in the neural networks
# Update rule for each parameter
for l in range(L):
### START CODE HERE ### (approx. 2 lines)
parameters["W" + str(l+1)] = parameters["W" + str(l+1)] - learning_rate*grads["dW" + str(l + 1)]
parameters["b" + str(l+1)] = parameters["b" + str(l+1)] - learning_rate*grads["db" + str(l + 1)]
### END CODE HERE ###
return parameters
GD를 변형해서 사용하기도 하는데, 지금 설명드릴 GD는 Stochastic Gradient Descent(SGD)입니다. 확률적 경사하강법이라고 불리는 SGD는 mini-batch GD에서 mini-batch의 크기가 1 example인 것과 동일합니다. update rule은 동일하지만, 차이점은 1개의 example에서 바로바로 gradient를 구해서 계산하는 것입니다.
아래는 Batch GD와 SGD의 코드입니다.
- (Batch) Gradient Descent
X = data_input
Y = labels
parameters = initialize_parameters(layers_dims)
for i in range(0, num_iterations):
# Forward propagation
a, caches = forward_propagation(X, parameters)
# Compute cost.
cost += compute_cost(a, Y)
# Backward propagation.
grads = backward_propagation(a, caches, parameters)
# Update parameters.
parameters = update_parameters(parameters, grads)- Stochastic Gradient Descent
X = data_input
Y = labels
parameters = initialize_parameters(layers_dims)
for i in range(0, num_iterations):
for j in range(0, m):
# Forward propagation
a, caches = forward_propagation(X[:,j], parameters)
# Compute cost
cost += compute_cost(a, Y[:,j])
# Backward propagation
grads = backward_propagation(a, caches, parameters)
# Update parameters.
parameters = update_parameters(parameters, grads)
SGD에서 1개의 training example을 사용해서 Gradient를 update합니다. 따라서, training set의 크기가 클 때, SGD는 더 빠를 수 있습니다. 그러나 최소값을 향해서 진행될 때, 부드럽게 수렴하지 않고 아래처럼 진동하면서 수렴하게 됩니다.
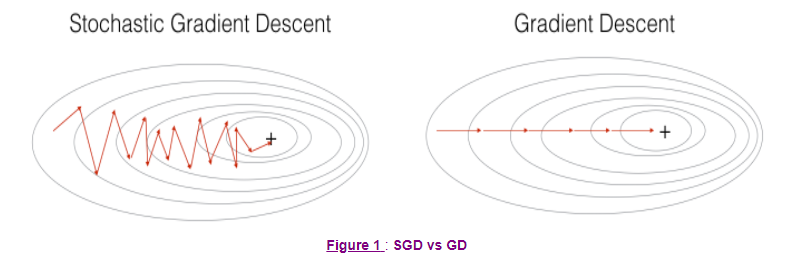
Deep learning에서 SGD는 총 3개의 for loop가 있습니다.
1. Number of iterations
2. m training examples
3. Number of layers
실제로 GD를 사용할 때, 전체 training set을 쓰지 않거나 1개의 training example을 쓰지 않으면(mini-batch 사용) 더 빠르게 결과를 얻을 수 있습니다. mini-batch는 1 ~ m 사이의 크기로 GD의 각 스텝을 진행하게 됩니다.

What you should remember:
- The difference between gradient descent, mini-batch gradient descent and stochastic gradient descent is the number of examples you use to perform one update step.
- You have to tune a learning rate hyperparameter αα.
- With a well-turned mini-batch size, usually it outperforms either gradient descent or stochastic gradient descent (particularly when the training set is large).
2. Mini-Batch Gradient Descent
mini-batch GD를 어떻게 구현하는지 살펴보도록 합시다.
mini-batch GD는 GD를 수행하기 전에, 우선 다음과 같은 2가지의 과정을 거치게 됩니다.
1. Shuffle
training set (X, Y)를 아래와 같이 섞어줍니다. X가 섞이는 것처럼 Y도 X와 동일하게 섞여야 label값이 섞이지 않으므로 주의해야합니다. 이 과정은 training example들이 다른 mini-batches로 무작위로 분리되도록 해주는 역할을 합니다.

2. Partition
1에서 섞인 (X, Y)를 mini_batch_size(여기서는 64)로 분리해줍니다. 항상 training examples의 수가 mini_batch_size로 나누어 떨어지지는 않기 때문에, 마지막 mini batch의 크기는 mini_batch_size보다 작을 수 있지만, 문제가 되지는 않습니다.
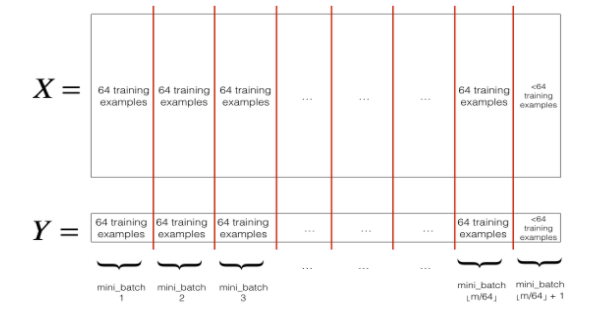
마지막 mini-batch는 mini_batch_size=64보다 작을 수 있기 때문에, 만약 전체 training example의 수가 mini_batch_size의 배수가 아니라면, 64개의 example로 가득 찬 \(\left \lfloor \frac{m}{\text{mini_batch_size}} \right \rfloor\) 개의 mini-batches가 있고, 마지막 mini-batch는 \(m - \text{mini_batch_size} \times \left \lfloor \frac{m}{\text{mini_batch_size}} \right \rfloor \)개의 example로 이루어져 있습니다.
코드는 다음과 같습니다.
# GRADED FUNCTION: random_mini_batches
def random_mini_batches(X, Y, mini_batch_size = 64, seed = 0):
"""
Creates a list of random minibatches from (X, Y)
Arguments:
X -- input data, of shape (input size, number of examples)
Y -- true "label" vector (1 for blue dot / 0 for red dot), of shape (1, number of examples)
mini_batch_size -- size of the mini-batches, integer
Returns:
mini_batches -- list of synchronous (mini_batch_X, mini_batch_Y)
"""
np.random.seed(seed) # To make your "random" minibatches the same as ours
m = X.shape[1] # number of training examples
mini_batches = []
# Step 1: Shuffle (X, Y)
permutation = list(np.random.permutation(m))
shuffled_X = X[:, permutation]
shuffled_Y = Y[:, permutation].reshape((1,m))
# Step 2: Partition (shuffled_X, shuffled_Y). Minus the end case.
num_complete_minibatches = math.floor(m/mini_batch_size) # number of mini batches of size mini_batch_size in your partitionning
for k in range(0, num_complete_minibatches):
### START CODE HERE ### (approx. 2 lines)
mini_batch_X = shuffled_X[:, k*mini_batch_size : (k+1)*mini_batch_size]
mini_batch_Y = shuffled_Y[:, k*mini_batch_size : (k+1)*mini_batch_size]
### END CODE HERE ###
mini_batch = (mini_batch_X, mini_batch_Y)
mini_batches.append(mini_batch)
# Handling the end case (last mini-batch < mini_batch_size)
if m % mini_batch_size != 0:
### START CODE HERE ### (approx. 2 lines)
mini_batch_X = shuffled_X[:, (k+1)*mini_batch_size:]
mini_batch_Y = shuffled_Y[:, (k+1)*mini_batch_size:]
### END CODE HERE ###
mini_batch = (mini_batch_X, mini_batch_Y)
mini_batches.append(mini_batch)
return mini_batches그래서 이전 실습 고양이 판별기 예제에서 입력 X의 크기가 (12288, 209) 였고, mini_batch_size = 64로 분리하게되면, 다음과 같은 결과를 얻을 수 있습니다.

What you should remember:
- Shuffling and Partitioning are the two steps required to build mini-batches
- Powers of two are often chosen to be the mini-batch size, e.g., 16, 32, 64, 128.
3. Momentum
mini-batch GD는 training example의 일부만으로 파라미터를 업데이트하기 때문에, 업데이트 방향의 변동이 꽤 있으며, 진동하면서 수렴하게 됩니다. 여기서 Momentum을 사용하면 이 진동을 감소시킬 수 있습니다.
Momentum은 부드럽게 업데이트하기 위해서 이전의 gradient를 사용합니다. 이전 gradient의 방향을 변수 v에 저장을 해서 사용하는 것이죠. 이것은 이전 step에서 gradients의 exponentially weighted average가 됩니다. 이 변수 v의 값은 언덕의 경사/경사방향에 따라 내리막으로 굴러가는 공의 '속도'라고 생각할 수 있습니다.

Momentum은 velocity, 변수 v를 0으로 초기화해서 진행합니다. 변수 v는 grads 딕셔너리와 같은 차원을 갖습니다.
# GRADED FUNCTION: initialize_velocity
def initialize_velocity(parameters):
"""
Initializes the velocity as a python dictionary with:
- keys: "dW1", "db1", ..., "dWL", "dbL"
- values: numpy arrays of zeros of the same shape as the corresponding gradients/parameters.
Arguments:
parameters -- python dictionary containing your parameters.
parameters['W' + str(l)] = Wl
parameters['b' + str(l)] = bl
Returns:
v -- python dictionary containing the current velocity.
v['dW' + str(l)] = velocity of dWl
v['db' + str(l)] = velocity of dbl
"""
L = len(parameters) // 2 # number of layers in the neural networks
v = {}
# Initialize velocity
for l in range(L):
### START CODE HERE ### (approx. 2 lines)
v["dW" + str(l+1)] = np.zeros(parameters["W"+str(l+1)].shape)
v["db" + str(l+1)] = np.zeros(parameters["b"+str(l+1)].shape)
### END CODE HERE ###
return v
이제, momentum으로 파라미터를 업데이트하는데, \(l = 1, ..., L\)에 대해서 아래와 같이 업데이트됩니다.
\[\left\{ \begin{matrix} v_{dW^{[l]}} = \beta v_{dW^{[l]}} + (1 - \beta)dW^{[l]} \\ W^{[l]} = W^{[l]} - \alpha v_{dW^{[l]}} \end{matrix}\right.\]
\[\left\{ \begin{matrix} v_{db^{[l]}} = \beta v_{db^{[l]}} + (1 - \beta)db^{[l]} \\ b^{[l]} = b^{[l]} - \alpha v_{db^{[l]}} \end{matrix}\right.\]
L은 layer의 수, \(beta\)는 momentum, \(\alpha\)는 learning rate입니다.
# GRADED FUNCTION: update_parameters_with_momentum
def update_parameters_with_momentum(parameters, grads, v, beta, learning_rate):
"""
Update parameters using Momentum
Arguments:
parameters -- python dictionary containing your parameters:
parameters['W' + str(l)] = Wl
parameters['b' + str(l)] = bl
grads -- python dictionary containing your gradients for each parameters:
grads['dW' + str(l)] = dWl
grads['db' + str(l)] = dbl
v -- python dictionary containing the current velocity:
v['dW' + str(l)] = ...
v['db' + str(l)] = ...
beta -- the momentum hyperparameter, scalar
learning_rate -- the learning rate, scalar
Returns:
parameters -- python dictionary containing your updated parameters
v -- python dictionary containing your updated velocities
"""
L = len(parameters) // 2 # number of layers in the neural networks
# Momentum update for each parameter
for l in range(L):
### START CODE HERE ### (approx. 4 lines)
# compute velocities
v["dW" + str(l+1)] = beta*v["dW" + str(l+1)] + (1 - beta)*grads["dW"+str(l+1)]
v["db" + str(l+1)] = beta*v["db" + str(l+1)] + (1 - beta)*grads["db"+str(l+1)]
# update parameters
parameters["W" + str(l+1)] = parameters["W" + str(l+1)] - learning_rate*v["dW" + str(l+1)]
parameters["b" + str(l+1)] = parameters["b" + str(l+1)] - learning_rate*v["db" + str(l+1)]
### END CODE HERE ###
return parameters, vvelocity는 0으로 초기화되기 때문에, build-up 과정을 위해서 몇 번의 iteration이 필요합니다.
만약 \(\beta = 0\)이라면, momentum이 없는 일반적인 GD입니다.
How do you choose \(\beta\)?
\(\beta\)값이 클수록, 더 많은 이전 gradients를 고려하기 때문에 더 부드럽게 업데이트됩니다. 그러나 \(\beta\)가 너무 크다면 너무 부드럽게 업데이트됩니다.
일반적인 \(\beta\)의 범위는 0.8에서 0.999 사이의 값입니다. 만약 튜닝하고 싶지 않다면, 0.9가 이상적인 기본값입니다.
Cost function J의 값을 줄이는 최적의 \(\beta\)를 찾으려면 여러 값을 시도해야합니다.
What you should remember:
- Momentum takes past gradients into account to smooth out the steps of gradient descent. It can be applied with batch gradient descent, mini-batch gradient descent or stochastic gradient descent.
- You have to tune a momentum hyperparameter ββ and a learning rate αα.
4. Adam
Adam은 NN을 학습하는데 가장 효과적인 최적화 알고리즘 중의 하나입니다. 이것은 RMSProp와 Momentum을 결합해서 사용합니다.
How does Adam work?
1. 이전 gradients의 exponentionally weighted average를 계산하고, 이 값을 변수 \(v\)(bias correction 하기 전)과 \(v^{\text{corrected}}\)(bias correction적용)에 저장합니다.
2. 이전 gradients의 exponentionally weighted average의 제곱을 계산하고, 이 값은 \(s\)(bias correction 하기 전)과 \(s^{\text{corrected}}\)(bias correction적용)에 저장합니다.
3. 1과 2에서 구한 값들을 사용해 파라미터를 업데이트합니다.
udpate rule은 다음과 같습니다.(for \(l = 1, ..., L\))
\[\left\{ \begin{align*} v_{dW^{[l]}} &= \beta_1 v_{dW^{[l]}} + (1 - \beta_1)\frac{\partial \mathscr{J}}{\partial W^{[l]}} \\ v_{dW^{[l]}}^{\text{corrected}} &= \frac{v_{dW^{[l]}}}{1 - (\beta_1)^t} \\ s_{dW^{[l]}} &= \beta_2 s_{dW^{[l]}} + (1 - \beta_2)(\frac{\partial \mathscr{J}}{\partial W^{[l]}})^2 \\ s_{dW^{[l]}}^{\text{corrected}} &= \frac{s_{dW^{[l]}}}{1 - (\beta_2)^t} \\ W^{[l]} &= W^{[l]} - \alpha \frac{v_{dW^{[l]}}^{\text{corrected}}}{\sqrt{s_{dW^{[l]}}^{\text{corrected}}} + \epsilon} \end{align*}\right.\]
where:
- t counts the number of steps taken of Adam
- L is the number of layers
- β1 and β2 are hyperparameters that control the two exponentially weighted averages.
- α is the learning rate
- ε is a very small number to avoid dividing by zero
\(v, s\)는 마찬가지로 0으로 초기화되고, grads의 크기와 동일합니다.
for \(l = 1, ..., L\) 에 대해서
v["dW" + str(l+1)] = ... #(numpy array of zeros with the same shape as parameters["W" + str(l+1)])
v["db" + str(l+1)] = ... #(numpy array of zeros with the same shape as parameters["b" + str(l+1)])
s["dW" + str(l+1)] = ... #(numpy array of zeros with the same shape as parameters["W" + str(l+1)])
s["db" + str(l+1)] = ... #(numpy array of zeros with the same shape as parameters["b" + str(l+1)])
로 업데이트 됩니다.
# GRADED FUNCTION: initialize_adam
def initialize_adam(parameters) :
"""
Initializes v and s as two python dictionaries with:
- keys: "dW1", "db1", ..., "dWL", "dbL"
- values: numpy arrays of zeros of the same shape as the corresponding gradients/parameters.
Arguments:
parameters -- python dictionary containing your parameters.
parameters["W" + str(l)] = Wl
parameters["b" + str(l)] = bl
Returns:
v -- python dictionary that will contain the exponentially weighted average of the gradient.
v["dW" + str(l)] = ...
v["db" + str(l)] = ...
s -- python dictionary that will contain the exponentially weighted average of the squared gradient.
s["dW" + str(l)] = ...
s["db" + str(l)] = ...
"""
L = len(parameters) // 2 # number of layers in the neural networks
v = {}
s = {}
# Initialize v, s. Input: "parameters". Outputs: "v, s".
for l in range(L):
### START CODE HERE ### (approx. 4 lines)
v["dW" + str(l+1)] = np.zeros(parameters["W" + str(l+1)].shape)
v["db" + str(l+1)] = np.zeros(parameters["b" + str(l+1)].shape)
s["dW" + str(l+1)] = np.zeros(parameters["W" + str(l+1)].shape)
s["db" + str(l+1)] = np.zeros(parameters["b" + str(l+1)].shape)
### END CODE HERE ###
return v, s그리고 update rule로 업데이트 합니다.
# GRADED FUNCTION: update_parameters_with_adam
def update_parameters_with_adam(parameters, grads, v, s, t, learning_rate = 0.01,
beta1 = 0.9, beta2 = 0.999, epsilon = 1e-8):
"""
Update parameters using Adam
Arguments:
parameters -- python dictionary containing your parameters:
parameters['W' + str(l)] = Wl
parameters['b' + str(l)] = bl
grads -- python dictionary containing your gradients for each parameters:
grads['dW' + str(l)] = dWl
grads['db' + str(l)] = dbl
v -- Adam variable, moving average of the first gradient, python dictionary
s -- Adam variable, moving average of the squared gradient, python dictionary
learning_rate -- the learning rate, scalar.
beta1 -- Exponential decay hyperparameter for the first moment estimates
beta2 -- Exponential decay hyperparameter for the second moment estimates
epsilon -- hyperparameter preventing division by zero in Adam updates
Returns:
parameters -- python dictionary containing your updated parameters
v -- Adam variable, moving average of the first gradient, python dictionary
s -- Adam variable, moving average of the squared gradient, python dictionary
"""
L = len(parameters) // 2 # number of layers in the neural networks
v_corrected = {} # Initializing first moment estimate, python dictionary
s_corrected = {} # Initializing second moment estimate, python dictionary
# Perform Adam update on all parameters
for l in range(L):
# Moving average of the gradients. Inputs: "v, grads, beta1". Output: "v".
### START CODE HERE ### (approx. 2 lines)
v["dW" + str(l+1)] = beta1*v["dW" + str(l+1)] + (1-beta1)*grads["dW" + str(l+1)]
v["db" + str(l+1)] = beta1*v["db" + str(l+1)] + (1-beta1)*grads["db" + str(l+1)]
### END CODE HERE ###
# Compute bias-corrected first moment estimate. Inputs: "v, beta1, t". Output: "v_corrected".
### START CODE HERE ### (approx. 2 lines)
v_corrected["dW" + str(l+1)] = v["dW"+str(l+1)] / (1 - beta1**(l+1))
v_corrected["db" + str(l+1)] = v["db"+str(l+1)] / (1 - beta1**(l+1))
### END CODE HERE ###
# Moving average of the squared gradients. Inputs: "s, grads, beta2". Output: "s".
### START CODE HERE ### (approx. 2 lines)
s["dW" + str(l+1)] = beta2*s["dW" + str(l+1)] + (1-beta2)*(grads["dW" + str(l+1)]**2)
s["db" + str(l+1)] = beta2*s["db" + str(l+1)] + (1-beta2)*(grads["db" + str(l+1)]**2)
### END CODE HERE ###
# Compute bias-corrected second raw moment estimate. Inputs: "s, beta2, t". Output: "s_corrected".
### START CODE HERE ### (approx. 2 lines)
s_corrected["dW" + str(l+1)] = s["dW"+str(l+1)] / (1 - beta2**(l+1))
s_corrected["db" + str(l+1)] = s["db"+str(l+1)] / (1 - beta2**(l+1))
### END CODE HERE ###
# Update parameters. Inputs: "parameters, learning_rate, v_corrected, s_corrected, epsilon". Output: "parameters".
### START CODE HERE ### (approx. 2 lines)
parameters["W" + str(l+1)] = parameters["W" + str(l+1)] - learning_rate * (v_corrected["dW" + str(l+1)] / (np.sqrt(s_corrected["dW" + str(l+1)]) + epsilon))
parameters["b" + str(l+1)] = parameters["b" + str(l+1)] - learning_rate * (v_corrected["db" + str(l+1)] / (np.sqrt(s_corrected["db" + str(l+1)]) + epsilon))
### END CODE HERE ###
return parameters, v, s
5. Moel with different optimization algorithms
지금까지 여러 버전의 최적화 알고리즘을 살펴보았는데, 알고리즘의 성능을 한번 살펴보도록 하겠습니다.
기본으로 3-layer NN을 사용하고,
- Mini-batch Gradient Descent
- Mini-batch Momentum
- Mini-batch Adam
이 3가지의 방법으로 학습해서 비교를 해보겠습니다.
이전 실습에서 사용했던 blue/red points의 경계를 나누는 모델로 학습을 하는데, 각 방법당 사용되는 함수는 다음과 같습니다.
- Mini-batch Gradient Descent: it will call your function:
- update_parameters_with_gd()
- Mini-batch Momentum: it will call your functions:
- initialize_velocity() and update_parameters_with_momentum()
- Mini-batch Adam: it will call your functions:
- initialize_adam() and update_parameters_with_adam()
def model(X, Y, layers_dims, optimizer, learning_rate = 0.0007, mini_batch_size = 64, beta = 0.9,
beta1 = 0.9, beta2 = 0.999, epsilon = 1e-8, num_epochs = 10000, print_cost = True):
"""
3-layer neural network model which can be run in different optimizer modes.
Arguments:
X -- input data, of shape (2, number of examples)
Y -- true "label" vector (1 for blue dot / 0 for red dot), of shape (1, number of examples)
layers_dims -- python list, containing the size of each layer
learning_rate -- the learning rate, scalar.
mini_batch_size -- the size of a mini batch
beta -- Momentum hyperparameter
beta1 -- Exponential decay hyperparameter for the past gradients estimates
beta2 -- Exponential decay hyperparameter for the past squared gradients estimates
epsilon -- hyperparameter preventing division by zero in Adam updates
num_epochs -- number of epochs
print_cost -- True to print the cost every 1000 epochs
Returns:
parameters -- python dictionary containing your updated parameters
"""
L = len(layers_dims) # number of layers in the neural networks
costs = [] # to keep track of the cost
t = 0 # initializing the counter required for Adam update
seed = 10 # For grading purposes, so that your "random" minibatches are the same as ours
m = X.shape[1] # number of training examples
# Initialize parameters
parameters = initialize_parameters(layers_dims)
# Initialize the optimizer
if optimizer == "gd":
pass # no initialization required for gradient descent
elif optimizer == "momentum":
v = initialize_velocity(parameters)
elif optimizer == "adam":
v, s = initialize_adam(parameters)
# Optimization loop
for i in range(num_epochs):
# Define the random minibatches. We increment the seed to reshuffle differently the dataset after each epoch
seed = seed + 1
minibatches = random_mini_batches(X, Y, mini_batch_size, seed)
cost_total = 0
for minibatch in minibatches:
# Select a minibatch
(minibatch_X, minibatch_Y) = minibatch
# Forward propagation
a3, caches = forward_propagation(minibatch_X, parameters)
# Compute cost and add to the cost total
cost_total += compute_cost(a3, minibatch_Y)
# Backward propagation
grads = backward_propagation(minibatch_X, minibatch_Y, caches)
# Update parameters
if optimizer == "gd":
parameters = update_parameters_with_gd(parameters, grads, learning_rate)
elif optimizer == "momentum":
parameters, v = update_parameters_with_momentum(parameters, grads, v, beta, learning_rate)
elif optimizer == "adam":
t = t + 1 # Adam counter
parameters, v, s = update_parameters_with_adam(parameters, grads, v, s,
t, learning_rate, beta1, beta2, epsilon)
cost_avg = cost_total / m
# Print the cost every 1000 epoch
if print_cost and i % 1000 == 0:
print ("Cost after epoch %i: %f" %(i, cost_avg))
if print_cost and i % 100 == 0:
costs.append(cost_avg)
# plot the cost
plt.plot(costs)
plt.ylabel('cost')
plt.xlabel('epochs (per 100)')
plt.title("Learning rate = " + str(learning_rate))
plt.show()
return parameters5.1 Mini-batch Gradient Descent
일반적인 mini-batch GD로 기본값인 64의 mini-batch size로 학습이 진행됩니다.
# train 3-layer model
layers_dims = [train_X.shape[0], 5, 2, 1]
parameters = model(train_X, train_Y, layers_dims, optimizer = "gd")
# Predict
predictions = predict(train_X, train_Y, parameters)
# Plot decision boundary
plt.title("Model with Gradient Descent optimization")
axes = plt.gca()
axes.set_xlim([-1.5,2.5])
axes.set_ylim([-1,1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)실행결과입니다.
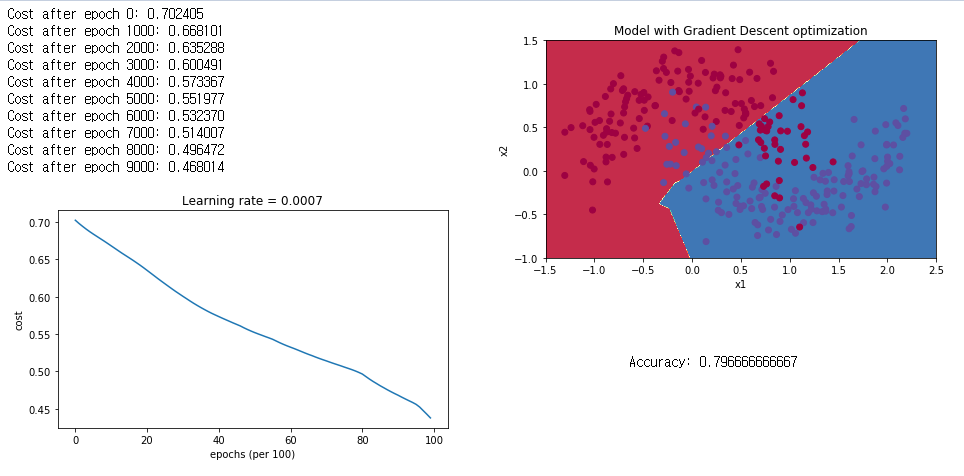
대략 80퍼센트의 정확도를 가지고 분류가 되었는데, 꽤 부정확한 결과를 얻었다고 볼 수 있겠네요.
5.2 Mini-batch Gradient Descent with momentum
이번에 확인할 방법은 momentum을 사용한 mini-batch GD입니다. size는 동일하게 64로 설정이 되고, 사용되는 beta의 값은 0.9입니다.
# train 3-layer model
layers_dims = [train_X.shape[0], 5, 2, 1]
parameters = model(train_X, train_Y, layers_dims, beta = 0.9, optimizer = "momentum")
# Predict
predictions = predict(train_X, train_Y, parameters)
# Plot decision boundary
plt.title("Model with Momentum optimization")
axes = plt.gca()
axes.set_xlim([-1.5,2.5])
axes.set_ylim([-1,1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)실행결과입니다.
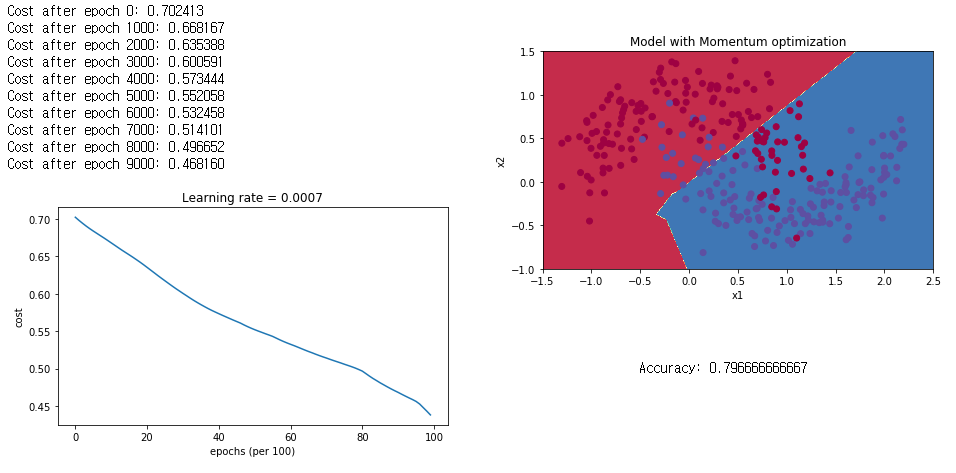
momentum을 추가로 사용했지만, 단순 mini-batch GD와는 큰 차이가 없는 결과를 얻었습니다.
5.3 Mini-batch with Adam mode
이번에는 Adam algorithm을 적용해서 학습해보도록 하겠습니다. 마찬가지로 mini-batch size는 64이고, beta1 = 0.9, beta2=0.999로 설정되어서 학습됩니다.
# train 3-layer model
layers_dims = [train_X.shape[0], 5, 2, 1]
parameters = model(train_X, train_Y, layers_dims, optimizer = "adam")
# Predict
predictions = predict(train_X, train_Y, parameters)
# Plot decision boundary
plt.title("Model with Adam optimization")
axes = plt.gca()
axes.set_xlim([-1.5,2.5])
axes.set_ylim([-1,1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)실행결과 입니다.
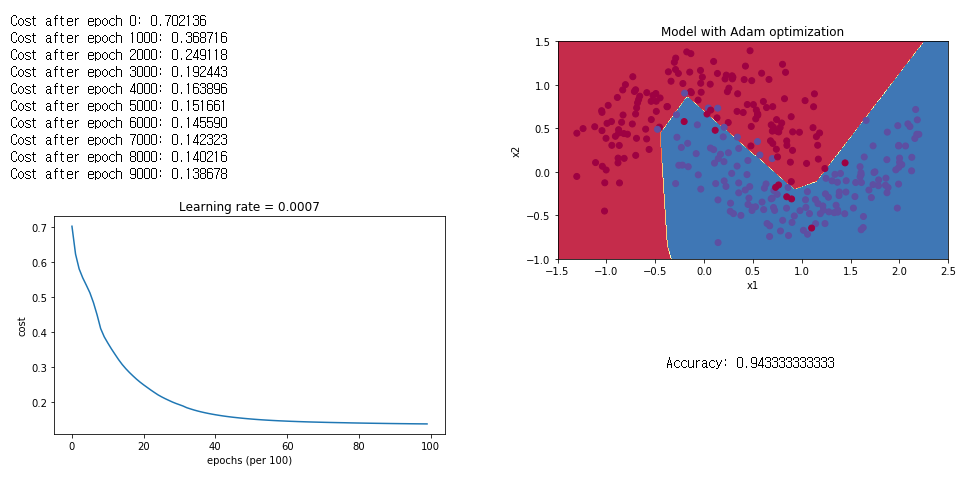
이전 2개의 방법보다 확실히 높은 정확도의 결과를 얻었습니다.
정리하자면 다음과 같습니다.
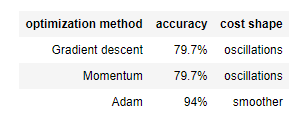
일반적으로 Momentum은 도움이 되지만, learning rate가 낮고 dataset이 단순하기 때문에 여기서 momentum의 효과가 미비합니다. 그리고 mini-batch에서는 cost가 꽤 많이 진동함을 볼 수 있습니다.
반면에, Adam algorithm은 확실히 mini-batch GD와 momentum보다 효과가 있는 방법입니다. 이렇게 간단한 dataset에서도 각 모델로 학습을 했을 때, 가장 좋은 결과를 얻을 수 있고, 훨씬 더 빨리 수렴하는 것을 볼 수 있습니다.
또한, Adam은 다음과 같은 장점도 가지고 있습니다.
- (mini-batch GD와 momentum보다는 높지만) 비교적 적은 메모리 사용
- (\(\alpha\)를 제외하고) 보통 하이퍼파라미터를 튜닝하지 않아도 잘 동작함
이상으로 3가지의 최적화 알고리즘을 살펴보았습니다.
'Coursera 강의 > Deep Learning' 카테고리의 다른 글
| Multi-class classification(Softmax regression) (0) | 2020.10.11 |
|---|---|
| Hyperparameter tuning / Batch Normalization (0) | 2020.10.10 |
| Optimization(최적화 알고리즘) : Mini-batch/Momentum/RMSprop/Adam (0) | 2020.10.02 |
| [실습] Gradient Checking (0) | 2020.09.26 |
| [실습] Regularization(L2 Regularization, Dropout) (0) | 2020.09.26 |




댓글