해당 내용은 Coursera의 딥러닝 특화과정(Deep Learning Specialization)의 두 번째 강의 Improving Deep Neural Networks: Hyperparameter tuning, Regularization and Optimization를 듣고 정리한 내용입니다. (Week 3)
- Multi-class classification
[Softmax Regression]
Softmax Regression이란 Logistic Regression의 일반화된 버전으로, 이진분류가 아닌 클래스가 여러개인 경우에 예측이 가능할 수 있도록 하는 모델이다.
고양이만 인식하는 것이 아니라, 강아지, 그리고 병아리를 인식하고 싶을 때 사용이 가능할 것이다.
고양이를 class 1, 강아지를 class 2, 병아리를 class 3이라고 하고, 3개의 클래스에도 해당이 되지 않으면 class 0이라고 하자.

여기서 새로운 표기법이 나오는데, 대문자 C를 사용해서 카테고리화하려는 클래스의 번호를 나타낸다.
위와 같은 경우에는 4가지의 class가 있다
C = # of classes = 4
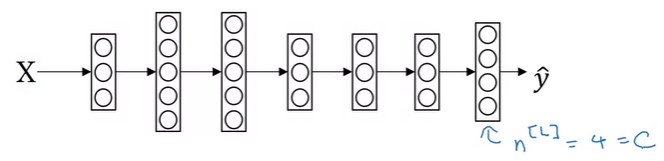
그리고 위와 같은 NN(neural network)이 있을 때, output layer의 unit의 개수는 4가 될 것이고, 일반적으로 C가 될 것이다. 이 output layer은 4개의 class들의 확률을 나타내는 것이고, 첫 번째 노드는 other class일 확률을 결과값으로 나타내고, 두 번째 unit은 고양이일 확률, 세번째 unit은 강아지일 확률, 네번째 unit은 병아리일 확률을 나타낸다.
4개의 결과값을 나타내기 위해서 output layer의 결과값 \(\hat{y}\)는 4x1의 dimension을 가지게 된다. 그리고 확률의 합은 1이여야 하기 때문에, \(\hat{y}\)에 있는 값들을 모두 합하면 1이 되어야 한다.
이렇게 위와 같이 여러 클래스에 대해서 확률값을 나타낼 수 있도록 하는 layer(위와 같이 4개의 hidden unit을 갖는)를 Softmax layer라고 한다.
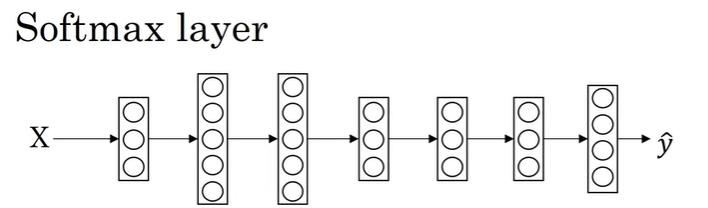
마지막 layer에서는 우선 linear 부분을 아래와 같이 계산한다.
\[z^{[L]} = W^{[L]}a^{[L-1]} + b^{[L]}\]
이렇게 \(z^{[L]}\)를 구했으면, Softmax activation 함수를 적용해야하는데, 이 activation 함수는 일반적인 activation과 약간 다르다. 다음과 같은 activation을 사용하게 된다.
Activation function(for softmax):
t = \(e^{(z^{[L]})}\)
\(a^{[L]} = \frac{e^{z^{[L]}}}{\sum_{i = 1}^{4} t_i}, a_i^{[L]} = \frac{t_i}{\sum_{i = 1}^{4} t_i}\)
\(a^{[L]}\)의 dimension은 당연히 4x1 vector이다.
\(z^{[L]}\)의 예시가 다음과 같이 구해졌을 때, 어떻게 구해지는지 살펴보자.
\[z^{[L]} = \begin{bmatrix} 5 \\ 2 \\ -1 \\ 3 \end{bmatrix}\]
여기서 vector t를 구하게 되면 다음과 같다.
\[t = \begin{bmatrix} e^5 \\ e^2 \\ e^{-1} \\ e^{3} \end{bmatrix} = \begin{bmatrix} 148.4 \\ 7.4 \\ 0.4 \\ 20.1 \end{bmatrix}\]
\[\sum_{i = 1}^{4} t_i = 176.3\]
그리고 \(a^{[L]}\)을 구하면 다음과 같이 구할 수 있을 것이다.
\[a^{[L]} = \frac{t}{176.3} = \begin{bmatrix} \frac{e^5}{176.3} = 0.842 \\ \frac{e^2}{176.3} = 0.042 \\ \frac{e^{-1}}{176.3} = 0.002 \\ \frac{e^3}{176.3} = 0.114 \end{bmatrix}\]
이렇게 구해진 확률값을 모두 더하면 1이되는 것을 확인할 수 있다.
이전 이진분류에서는 activation 함수가 single row의 값을 입력으로 받았지만, Softmax Regression에서는 입력도 벡터의 값이며, 결과값도 벡터로 나타난다.
이번에는 hidden layer가 없는 Softmax Regression 예시를 살펴보자.(C = 3)

입력으로 \(x_1, x_2\)가질 때, 위 모델은 다음과 같이 계산될 것이다.
\[\begin{align*} z^{[1]} &= W^{[1]}x + b^{[1]} \\ a^{[1]} &= \hat{y} = g(z^{[1]}) \end{align*}\]
그래서 C = 3일 때, 아래와 같은 Decision Boundary를 가질 수 있다.

위 Decision Boundary는 Logistic Regression과 유사한데, 각 클래스간의 Decision Boundary가 선형적으로 나타난다. 결국 2개의 클래스 간의 decision boundary가 선형인 것이다.
C = 4, 5, 6인 경우에는 다음과 같이 나타날 수 있다.

당연히 deep nueral network에서 hidden layer, hidden unit이 더 많은 경우에는 더 복잡한 비선형 decision boundary를 갖는 것도 가능하다.
[Training a softmax classifier]
이전 예제에서 우리는 \(z^{[L]}\)을 사용해서 4개의 클래스의 확률을 아래와 같이 구했다.

hardmax의 경우에는 [1 0 0 0] 처럼 값을 가지는데, 가장 큰 확률을 가지는 요소가 1이 되고 나머지는 0이 되는 반면에, Softmax는 각 클래스의 확률을 값으로 가지며, Softmax Regression은 C개의 클래스를 가진 Logistic Regression을 일반화한 것이라고 할 수 있다. 만약 C=2라면, Softmax Regression은 Logistic Regression과 동일한 것이다.
이제 실제로 softmax layer로 어떻게 학습시키는지 알아보자.
우선 학습을 하는데 필요한 Loss Function을 예시를 정의해보겠다.
만약 sample에 대한 \(y\)의 값과 예측값 \(\hat{y}\)가 아래와 같이 예측되었을 때를 살펴보자.
\[y = \begin{bmatrix} 0 \\ 1 \\ 0 \\ 0 \end{bmatrix}, a^{[L]} = \hat{y} = \begin{bmatrix} 0.3 \\ 0.2 \\ 0.1 \\ 0.4 \end{bmatrix}\]
아마 이러한 결과로 예측했다면, 잘 예측은 하지 못한 것이라고 할 수 있을 것이다.
주로 사용되는 Loss Function은 다음과 같다.
\[\mathscr{L}(\hat{y}, y) = -\sum_{j = 1}^{4}y_j log\hat{y}_j\]
위 예시에서는 \(y_1 = y_3 = y_4 = 0, y_2 = 1\) 이고, 고양이로 분류된 sample이고 결국 Loss function은 \(y_2\)에 대한 항만 남고 나머지는 0이 되어서 다음과 같이 계산된다.
\[\mathscr{L}(\hat{y}, y) = -y_2 log\hat{y}_2 = -log\hat{y}_2\]
그렇다면 Loss를 줄이려고 한다면, \(\hat{y}_2\)를 최대한 크게 만들어야 한다.
지금까지 한 개의 training example에 대한 Loss를 구했고, 전체 training set에 대해서는 모든 training set의 Loss 합을 더해서 구하게 된다.
\[J(W^{[1]}, b^{[1]}, \cdots) = \frac{1}{m}\sum_{i = 1}^{m}\mathscr{L}(\hat{y}^{(i)}, y^{(i)})\]
마지막으로 softmax에서 어떻게 Gradient Descent를 적용하는지 살펴보자.
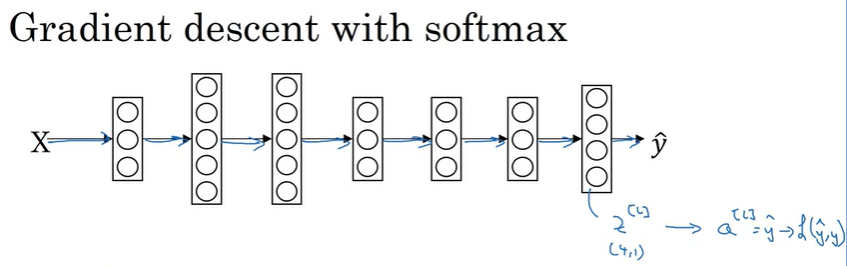
위와 같은 NN이 있을 때, output layer의 결과값은 FP를 통해서 \(z^{[L]} \rightarrow a^{[L]} = \hat{y}\)을 구하고, 이렇게 구한 값을 사용해 Loss \(\mathscr{L}(\hat{y}, y)\)를 계산한다.
그리고 BP와 GD를 구해야하는데, 여기서 BP를 위해 초기화해야하는 값은 output layer에서의 z의 derivative(미분항)이며, 이것은 다음과 같이 구할 수 있다.
\[dz^{[L]} = \hat{y} - y\]
마찬가지로 \(dz^{[L]}\)은 (4, 1) vector이고 구한 값을 사용해서 BP를 진행하고 NN에서 필요한 derivative를 구하면 된다.(NN의 BP는 이전 강의 참조하면 될 것 같습니다)
'Coursera 강의 > Deep Learning' 카테고리의 다른 글
| ML Strategy 2-1 (Error Analysis, Data mismatched) (0) | 2020.10.28 |
|---|---|
| ML Strategy 1(orthogonalization, evaluation metric, human-level performance) (0) | 2020.10.25 |
| Hyperparameter tuning / Batch Normalization (0) | 2020.10.10 |
| [실습] Optimization Methods(Mini-batch, Momentum, Adam Algorithm) (0) | 2020.10.02 |
| Optimization(최적화 알고리즘) : Mini-batch/Momentum/RMSprop/Adam (0) | 2020.10.02 |




댓글