해당 내용은 Coursera의 딥러닝 특화과정(Deep Learning Specialization)의 첫 번째 강의 Neural Networks and Deep Learning을 듣고 정리한 내용입니다. (Week 4)
4주차 두 번째 실습은 이전 실습에서 구현한 NN의 step by step 함수들을 사용해서 첫 번째 실습에서 Logistic Regression으로 구현한 cat vs non-cat 분류기를 NN으로 구현해볼 것입니다.
1. Packages
사용되는 패키지는 다음과 같습니다.
- numpy is the fundamental package for scientific computing with Python.
- matplotlib is a library to plot graphs in Python.
- h5py is a common package to interact with a dataset that is stored on an H5 file.
- PIL and scipy are used here to test your model with your own picture at the end.
- dnn_app_utils provides the functions implemented in the "Building your Deep Neural Network: Step by Step" assignment to this notebook.
- np.random.seed(1) is used to keep all the random function calls consistent. It will help us grade your work.
import time
import numpy as np
import h5py
import matplotlib.pyplot as plt
import scipy
from PIL import Image
from scipy import ndimage
from dnn_app_utils_v3 import *
%matplotlib inline
plt.rcParams['figure.figsize'] = (5.0, 4.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'
%load_ext autoreload
%autoreload 2
np.random.seed(1)
2. Dataset
이미 이전에 Cat vs non-Cat dataset을 살펴봤을거라고 생각하고, 바로 데이터를 읽어보도록 하겠습니다.
train_x_orig, train_y, test_x_orig, test_y, classes = load_data()데이터를 읽어오고 sample 하나를 무작위로 살펴보죠.

새 사진이고, 고양이가 아니기 때문에 label은 0입니다.
dataset의 shape를 살펴보겠습니다.
# Explore your dataset
m_train = train_x_orig.shape[0]
num_px = train_x_orig.shape[1]
m_test = test_x_orig.shape[0]
print ("Number of training examples: " + str(m_train))
print ("Number of testing examples: " + str(m_test))
print ("Each image is of size: (" + str(num_px) + ", " + str(num_px) + ", 3)")
print ("train_x_orig shape: " + str(train_x_orig.shape))
print ("train_y shape: " + str(train_y.shape))
print ("test_x_orig shape: " + str(test_x_orig.shape))
print ("test_y shape: " + str(test_y.shape))
training set의 개수는 209개이며, test set의 개수는 50개입니다.
그리고 각 sample은 64px x 64px x 3(RGB) 로 이루어져 있으며, 우리는 3차원으로 이루어진 입력값을 1차원의 벡터로 변환하는 작업을 해야합니다.
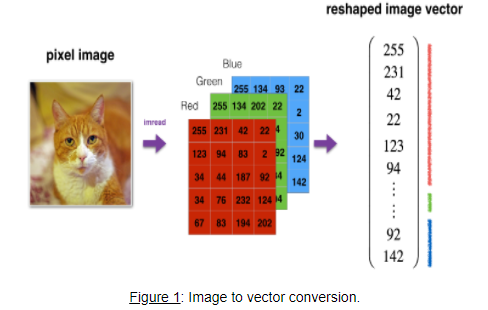
# Reshape the training and test examples
train_x_flatten = train_x_orig.reshape(train_x_orig.shape[0], -1).T # The "-1" makes reshape flatten the remaining dimensions
test_x_flatten = test_x_orig.reshape(test_x_orig.shape[0], -1).T
# Standardize data to have feature values between 0 and 1.
train_x = train_x_flatten/255.
test_x = test_x_flatten/255.
print ("train_x's shape: " + str(train_x.shape))
print ("test_x's shape: " + str(test_x.shape))
(64 x 64 x 3) 크기를 갖는 입력을 (12288 x 1)로 변환했습니다.
3. Architecture of your model
NN을 구성할 텐데, NN 크기에 따라 정확도가 어떻게 되는지 비교하기 위해서 2-layer의 NN과 L-layer의 deep NN을 각각 구성해보도록 하겠습니다.
3.1 2-layer neural network
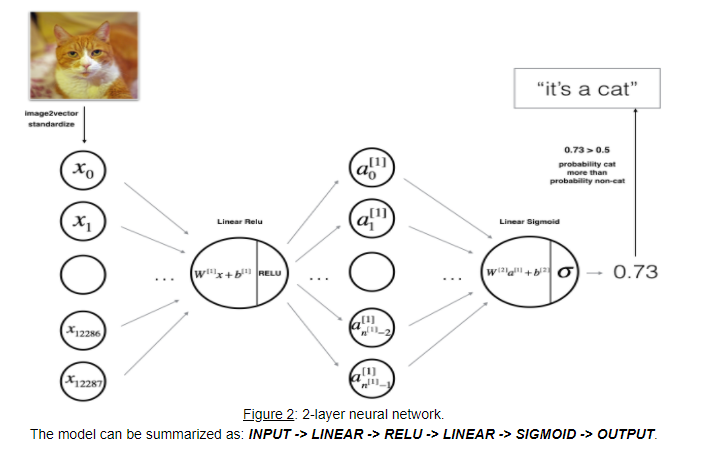
2-layer NN은 위와 같은 구성을 갖습니다.
input은 (12288, 1)의 크기(하나의 샘플의 경우)를 갖고, layer 1의 파라미터 \(W^{[1]}\)의 크기는 \((n^{[l]}, 12288)\)가 됩니다.
input X는 아래와 같이 구성되겠죠.
\[\begin{bmatrix} | && | && && | \\ x^{(1)T} && x^{(2)T} && \cdots && x^{(209)T} \\ | && | && && | \end{bmatrix}\]
\(W^{[1]}X + b^{[1]}\)를 구하고, ReLU 함수를 통해 activation \(\left [ a_0^{[1]}, a_1^{[2]}, \cdots, a_{n^{[1]} -1}^{[1]} \right ]^T\)를 구합니다.
그리고, 같은 과정을 통해서 구한 activation으로 \(W^{[2]}\)를 곱하고 \(b^{[2]}\)를 더해줍니다.
마지막으로 sigmoid 함수를 통해서 결과값을 얻습니다. 만약 이 값이 0.5보다 크다면, 고양이(1)로 분류합니다.
3.2 L-layer deep neural network
L-layer를 가진 deep NN은 아래와 같이 구성됩니다.

L-1개의 hidden layer(ReLU activation)와 output layer(sigmoid activation)으로 이루어져 있습니다.
마찬가지로 동일한 입력 X(\(A^{[0]}\))를 가지고, \(W^{[l]}A^{[l-1]} + b^{[l]}\)를 구하고, activation function(ReLU)를 통해 \(A^{[l]}\)을 구하는 작업을 L-1번 반복합니다.
그리고 마지막 ouput layer에서 \(W^{[l]}A^{[l-1]} + b^{[l]}\)는 동일하지만, sigmoid activation을 통해 결과값을 얻습니다. 마찬가지로 이 값이 0.5보다 크다면 고양이(1)로 분류됩니다.
3.3 General methodology
정리하면 다음과 같은 과정으로 진행됩니다.
1. Initialize parameters / Define hyperparameters
2. Loop for num_iterations:
a. Forward propagtaion
b. Compute cost function
c. Backward propagation
d. Update parameters (using parameters, and grads from BP)
4. Use trained parameters to predict labels
4. Two-layer neural network
2-layer NN부터 구성해보도록 합시다.
Linear -> ReLU -> Linear -> Sigmoid의 구조를 갖고 사용되는 함수는 다음과 같습니다.
def initialize_parameters(n_x, n_h, n_y):
...
return parameters
def linear_activation_forward(A_prev, W, b, activation):
...
return A, cache
def compute_cost(AL, Y):
...
return cost
def linear_activation_backward(dA, cache, activation):
...
return dA_prev, dW, db
def update_parameters(parameters, grads, learning_rate):
...
return parameters이 함수는 이전 실습에서 구현했기 때문에, 이전 게시글을 참조바랍니다.
2020/09/25 - [Coursera 강의/Deep Learning] - [실습] Building Deep Neural Network : Step by Step
input, hidden, output layer의 크기는 다음과 같이 정의됩니다.
### CONSTANTS DEFINING THE MODEL ####
n_x = 12288 # num_px * num_px * 3
n_h = 7
n_y = 1
layers_dims = (n_x, n_h, n_y)그리고 2-layer model은 다음과 같습니다.
# GRADED FUNCTION: two_layer_model
def two_layer_model(X, Y, layers_dims, learning_rate = 0.0075, num_iterations = 3000, print_cost=False):
"""
Implements a two-layer neural network: LINEAR->RELU->LINEAR->SIGMOID.
Arguments:
X -- input data, of shape (n_x, number of examples)
Y -- true "label" vector (containing 1 if cat, 0 if non-cat), of shape (1, number of examples)
layers_dims -- dimensions of the layers (n_x, n_h, n_y)
num_iterations -- number of iterations of the optimization loop
learning_rate -- learning rate of the gradient descent update rule
print_cost -- If set to True, this will print the cost every 100 iterations
Returns:
parameters -- a dictionary containing W1, W2, b1, and b2
"""
np.random.seed(1)
grads = {}
costs = [] # to keep track of the cost
m = X.shape[1] # number of examples
(n_x, n_h, n_y) = layers_dims
# Initialize parameters dictionary, by calling one of the functions you'd previously implemented
### START CODE HERE ### (≈ 1 line of code)
parameters = initialize_parameters(n_x, n_h, n_y)
### END CODE HERE ###
# Get W1, b1, W2 and b2 from the dictionary parameters.
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
# Loop (gradient descent)
for i in range(0, num_iterations):
# Forward propagation: LINEAR -> RELU -> LINEAR -> SIGMOID. Inputs: "X, W1, b1, W2, b2". Output: "A1, cache1, A2, cache2".
### START CODE HERE ### (≈ 2 lines of code)
A1, cache1 = linear_activation_forward(X, W1, b1, activation = "relu")
A2, cache2 = linear_activation_forward(A1, W2, b2, activation = "sigmoid")
### END CODE HERE ###
# Compute cost
### START CODE HERE ### (≈ 1 line of code)
cost = compute_cost(A2, Y)
### END CODE HERE ###
# Initializing backward propagation
dA2 = - (np.divide(Y, A2) - np.divide(1 - Y, 1 - A2))
# Backward propagation. Inputs: "dA2, cache2, cache1". Outputs: "dA1, dW2, db2; also dA0 (not used), dW1, db1".
### START CODE HERE ### (≈ 2 lines of code)
dA1, dW2, db2 = linear_activation_backward(dA2, cache2, activation="sigmoid")
dA0, dW1, db1 = linear_activation_backward(dA1, cache1, activation="relu")
### END CODE HERE ###
# Set grads['dWl'] to dW1, grads['db1'] to db1, grads['dW2'] to dW2, grads['db2'] to db2
grads['dW1'] = dW1
grads['db1'] = db1
grads['dW2'] = dW2
grads['db2'] = db2
# Update parameters.
### START CODE HERE ### (approx. 1 line of code)
parameters = update_parameters(parameters, grads, learning_rate)
### END CODE HERE ###
# Retrieve W1, b1, W2, b2 from parameters
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
# Print the cost every 100 training example
if print_cost and i % 100 == 0:
print("Cost after iteration {}: {}".format(i, np.squeeze(cost)))
if print_cost and i % 100 == 0:
costs.append(cost)
# plot the cost
plt.plot(np.squeeze(costs))
plt.ylabel('cost')
plt.xlabel('iterations (per hundreds)')
plt.title("Learning rate =" + str(learning_rate))
plt.show()
return parametersHyperparameter인 learning_rate는 0.0075, iterations은 3000으로 기본설정되어 있습니다.
이 함수는 매 순회마다 FP, Cost계산, BP, 파라미터 update 과정을 거쳐서 학습을 하게됩니다.
매 순회마다 입력 X, 파라미터 W1, b1, 그리고 activation 함수(ReLU)를 통해 A1을 구하고,
마찬가지로 W2, b2, 그리고 Sigmoid 함수를 통해서 A2, 즉, \(\hat{Y}\)를 구합니다.
그리고 A2와 실제 라벨 Y를 가지고 cost를 계산합니다.
이 후에 dA2와 Y를 가지고 dA2를 먼저 구하고, dA2와 FP에서 구한 계산값들을 가지고 dA1, dW2, db2를 구하고, 첫 번째 layer에서 dA0, dW1, db1을 구합니다. 여기서 dA0은 사용하지 않는 값(입력X에 대한 Gradient이기 때문에)입니다.
그리고 이렇게 구한 gradient를 가지고 파라미터 W, b를 업데이트하면 한 번의 루프가 완료됩니다.
parameters = two_layer_model(train_x, train_y, layers_dims = (n_x, n_h, n_y), num_iterations = 2500, print_cost=True)이렇게 구현한 함수를 실행(learning rate = 0.0075, iteration = 2500)하면, 우리는 다음과 같은 결과를 얻을 수 있습니다.
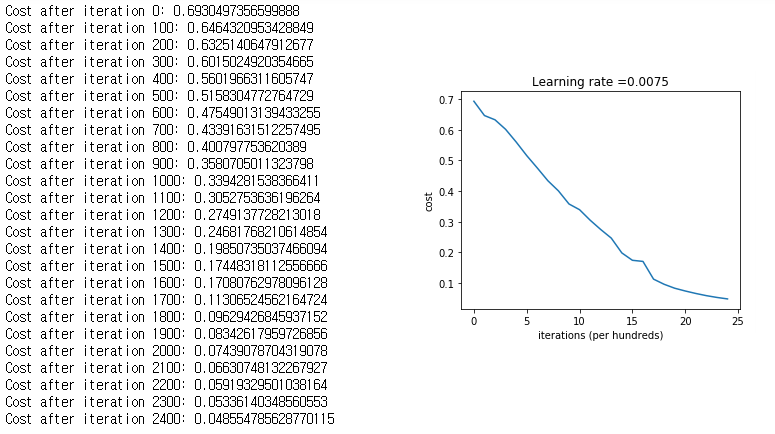
매 iteration마다 cost가 감소하는 것을 볼 수 있습니다.
이렇게 학습된 모델을 가지고 training set으로 예측해보면 100%의 정확도를 얻을 수 있습니다.

test set으로 예측해보면 72%의 정확도를 얻습니다.

위 결과를 봤을 때, 모델이 training set에 overfitting되어 있는 것으로 추측됩니다. iteration을 1500회로 감소해서 학습한다면, overfitting을 막을 수 있을 것 같은데, 결과를 보도록 하겠습니다.



예상 외로 정확도가 오히려 더 떨어졌습니다.. !
5. L-layer Neural Network
이번엔 L-layer NN을 구현해보도록 하겠습니다. 사용되는 함수는 다음과 같으며, 자세한 함수 내용은 이전 게시글을 참조하시기 바랍니다.
def initialize_parameters_deep(layers_dims):
...
return parameters
def L_model_forward(X, parameters):
...
return AL, caches
def compute_cost(AL, Y):
...
return cost
def L_model_backward(AL, Y, caches):
...
return grads
def update_parameters(parameters, grads, learning_rate):
...
return parameters4-layer model을 구현하도록 하겠습니다. 각각의 layer의 size는 다음과 같습니다.
### CONSTANTS ###
layers_dims = [12288, 20, 7, 5, 1] # 4-layer model모델은 아래와 같이 구현됩니다.
# GRADED FUNCTION: L_layer_model
def L_layer_model(X, Y, layers_dims, learning_rate = 0.0075, num_iterations = 3000, print_cost=False):#lr was 0.009
"""
Implements a L-layer neural network: [LINEAR->RELU]*(L-1)->LINEAR->SIGMOID.
Arguments:
X -- data, numpy array of shape (num_px * num_px * 3, number of examples)
Y -- true "label" vector (containing 0 if cat, 1 if non-cat), of shape (1, number of examples)
layers_dims -- list containing the input size and each layer size, of length (number of layers + 1).
learning_rate -- learning rate of the gradient descent update rule
num_iterations -- number of iterations of the optimization loop
print_cost -- if True, it prints the cost every 100 steps
Returns:
parameters -- parameters learnt by the model. They can then be used to predict.
"""
np.random.seed(1)
costs = [] # keep track of cost
# Parameters initialization. (≈ 1 line of code)
### START CODE HERE ###
parameters = initialize_parameters_deep(layers_dims)
### END CODE HERE ###
# Loop (gradient descent)
for i in range(0, num_iterations):
# Forward propagation: [LINEAR -> RELU]*(L-1) -> LINEAR -> SIGMOID.
### START CODE HERE ### (≈ 1 line of code)
AL, caches = L_model_forward(X, parameters)
### END CODE HERE ###
# Compute cost.
### START CODE HERE ### (≈ 1 line of code)
cost = compute_cost(AL, Y)
### END CODE HERE ###
# Backward propagation.
### START CODE HERE ### (≈ 1 line of code)
grads = L_model_backward(AL, Y, caches)
### END CODE HERE ###
# Update parameters.
### START CODE HERE ### (≈ 1 line of code)
parameters = update_parameters(parameters, grads, learning_rate)
### END CODE HERE ###
# Print the cost every 100 training example
if print_cost and i % 100 == 0:
print ("Cost after iteration %i: %f" %(i, cost))
if print_cost and i % 100 == 0:
costs.append(cost)
# plot the cost
plt.plot(np.squeeze(costs))
plt.ylabel('cost')
plt.xlabel('iterations (per hundreds)')
plt.title("Learning rate =" + str(learning_rate))
plt.show()
return parameters수행되는 과정은 2-layer와 거의 동일하며, 중간 hidden layer에서의 과정이 L-1번 반복되는 것 뿐입니다.
training set에서 구현한 모델을 학습해보도록 합시다.
parameters = L_layer_model(train_x, train_y, layers_dims, num_iterations = 2500, print_cost = True)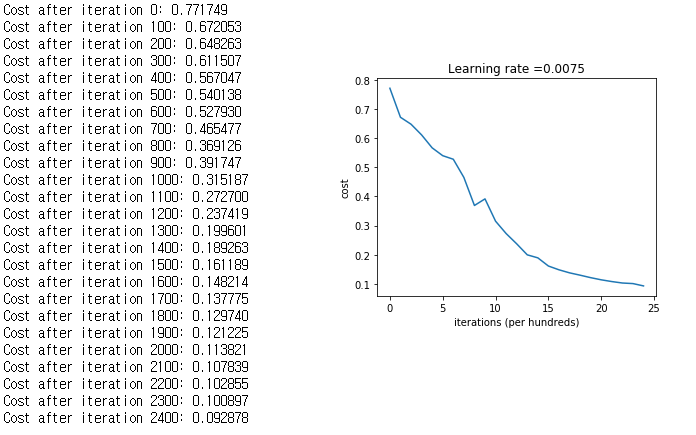
2-layer일 때보다 최종 Cost는 두배가량 더 큽니다.
training set과 test set에서 예측한 결과값을 실제 label과 비교해보겠습니다.


training set의 정확도는 98%, test set의 정확도는 80%로 꽤 많이 향상되었습니다.
hidden layer가 더 많을 때, 더 좋은 결과가 나타나는 것을 볼 수 있네요.
6. Results Analysis
정확도가 80%이기 때문에 잘못 예측하기도 하는데, 잘못 예측된 예시들을 살펴보도록 합시다.

이러한 사진들은 다음과 같은 특징을 가집니다.
- 고양이의 자세가 이상한 경우
- 배경과 유사한 색을 가진 고양이
- 보통 고양이의 색이 아니거나 흔한 종이 아닌 경우
- 카메라의 각도의 문제
- 사진의 밝기가 어두운 경우
- 사진의 고양이가 매우 크거나 작은 경우
이상으로 2-layer와 4-layer의 NN을 살펴보았습니다.
'Coursera 강의 > Deep Learning' 카테고리의 다른 글
| [실습] Regularization(L2 Regularization, Dropout) (0) | 2020.09.26 |
|---|---|
| [실습] Initialization 초기화 (0) | 2020.09.26 |
| [실습] Building Deep Neural Network : Step by Step (0) | 2020.09.25 |
| [실습] Planar data classification with a hidden layer (9) | 2020.09.25 |
| [실습] Logistic Regression with a Neural Network(can / non-cat classifier) (0) | 2020.09.24 |




댓글