해당 내용은 Coursera의 딥러닝 특화과정(Deep Learning Specialization)의 첫 번째 강의 Neural Networks and Deep Learning를 듣고 정리한 내용입니다. (Week 4)
4주차 첫 번째 실습은 딥러닝을 순서대로 구현해보는 것입니다.
여기서 ouput layer를 제외한 layer에서 activation function을 ReLU함수를 사용하고, output layer에서만 sigmoid 함수를 사용할 것이고, 이번 실습에서는 2-layer와 L-layer를 위한 함수를 각각 구현할 것입니다.
시작하기에 앞서 표기법을 정리하겠습니다.
- 위첨자 \([l]\)은 \(l^{th}\) layer를 의미합니다. \(a^{[L]}\)은 L번째 layer의 activation을 의미합니다.
- 위첨자 \((l)\)은 \(i^{th}\) sample을 의미합니다.
- 아래첨자 i는 \(i^{th}\) 번째 vector를 의미합니다. \(a_i^{[l]}\)라면 l번째 layer의 i번째 activation 입니다.
1. Packages
이번 실습에서 사용되는 패키지는 다음과 같습니다.
- numpy is the main package for scientific computing with Python.
- matplotlib is a library to plot graphs in Python.
- dnn_utils provides some necessary functions for this notebook.
- testCases provides some test cases to assess the correctness of your functions
- np.random.seed(1) is used to keep all the random function calls consistent. It will help us grade your work. Please don't change the seed.
dnn_utils에서 FP와 BP에서 사용되는 activation 함수를 제공하고 있으며, 아래와 같이 정의되어 있습니다.
import numpy as np
def sigmoid(Z):
"""
Implements the sigmoid activation in numpy
Arguments:
Z -- numpy array of any shape
Returns:
A -- output of sigmoid(z), same shape as Z
cache -- returns Z as well, useful during backpropagation
"""
A = 1/(1+np.exp(-Z))
cache = Z
return A, cache
def relu(Z):
"""
Implement the RELU function.
Arguments:
Z -- Output of the linear layer, of any shape
Returns:
A -- Post-activation parameter, of the same shape as Z
cache -- a python dictionary containing "A" ; stored for computing the backward pass efficiently
"""
A = np.maximum(0,Z)
assert(A.shape == Z.shape)
cache = Z
return A, cache
def relu_backward(dA, cache):
"""
Implement the backward propagation for a single RELU unit.
Arguments:
dA -- post-activation gradient, of any shape
cache -- 'Z' where we store for computing backward propagation efficiently
Returns:
dZ -- Gradient of the cost with respect to Z
"""
Z = cache
dZ = np.array(dA, copy=True) # just converting dz to a correct object.
# When z <= 0, you should set dz to 0 as well.
dZ[Z <= 0] = 0
assert (dZ.shape == Z.shape)
return dZ
def sigmoid_backward(dA, cache):
"""
Implement the backward propagation for a single SIGMOID unit.
Arguments:
dA -- post-activation gradient, of any shape
cache -- 'Z' where we store for computing backward propagation efficiently
Returns:
dZ -- Gradient of the cost with respect to Z
"""
Z = cache
s = 1/(1+np.exp(-Z))
dZ = dA * s * (1-s)
assert (dZ.shape == Z.shape)
return dZ
그리고 적용되는 라이브러리 입니다.
import numpy as np
import h5py
import matplotlib.pyplot as plt
from testCases_v4a import *
from dnn_utils_v2 import sigmoid, sigmoid_backward, relu, relu_backward
%matplotlib inline
plt.rcParams['figure.figsize'] = (5.0, 4.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'
%load_ext autoreload
%autoreload 2
np.random.seed(1)
2. Outline of the Assignment
시작하기에 앞서 오늘 실습의 개요를 살펴보겠습니다.
NN을 구현하기 위해서, 우리는 이번에 Helper function들을 정의할 것이고, 이 정의된 함수들은 다음 과제에서 2-layer NN과 L-layer NN을 구현하는데 사용할 것입니다.
구현되는 함수는 다음과 같습니다.
- L-layer의 파라미터 초기화 함수
- Forward Propagation 수행 함수
- Cost 계산 함수
- Backward Propagation 수행 함수
- 파라미터 업데이트 함수

위와 같은 과정을 거치게 됩니다. L-1 layer(hidden layers)에서는 ReLU함수를 activation function으로 사용했고, 마지막 ouput layer에서는 Sigmoid 함수를 사용한 것을 볼 수 있습니다.
3. Initialization
3.1 2-layer Neural Network
2-layer NN의 파라미터 초기화를 위한 함수를 구현해봅시다.
model의 구조는 Linear -> ReLU -> Linear -> Sigmoid 로 구성되며, 우리는 numpy의 random.randn(shape)*0.01로 랜덤하게 초기화할 수 있습니다. 이전의 실습과 마찬가지로 파라미터 b는 0으로 초기화해도 무관합니다.
# GRADED FUNCTION: initialize_parameters
def initialize_parameters(n_x, n_h, n_y):
"""
Argument:
n_x -- size of the input layer
n_h -- size of the hidden layer
n_y -- size of the output layer
Returns:
parameters -- python dictionary containing your parameters:
W1 -- weight matrix of shape (n_h, n_x)
b1 -- bias vector of shape (n_h, 1)
W2 -- weight matrix of shape (n_y, n_h)
b2 -- bias vector of shape (n_y, 1)
"""
np.random.seed(1)
### START CODE HERE ### (≈ 4 lines of code)
W1 = np.random.randn(n_h, n_x) * 0.01
b1 = np.zeros((n_h, 1))
W2 = np.random.randn(n_y, n_h) * 0.01
b2 = np.zeros((n_y, 1))
### END CODE HERE ###
assert(W1.shape == (n_h, n_x))
assert(b1.shape == (n_h, 1))
assert(W2.shape == (n_y, n_h))
assert(b2.shape == (n_y, 1))
parameters = {"W1": W1,
"b1": b1,
"W2": W2,
"b2": b2}
return parameters
3.2 L-layer Neural Network
다음으로 L-layer를 가진 NN을 구현해봅시다.
L-layer의 파라미터를 초기화하는 것은 조금 더 복잡한데, 각 layer에서의 파라미터 W와 b의 차원을 맞추어 주어야하기 때문입니다. \(n^{[l]}\)이 l-layer의 unit 갯수라는 것을 기억하면서 이전 실습이었던 고양이 판별기를 예시로 살펴보면 다음과 같이 각 layer의 파라미터 차원을 구할 수 있습니다.(입력 X의 차원이 (12288, 209)(with m = 209 examples))

# GRADED FUNCTION: initialize_parameters_deep
def initialize_parameters_deep(layer_dims):
"""
Arguments:
layer_dims -- python array (list) containing the dimensions of each layer in our network
Returns:
parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL":
Wl -- weight matrix of shape (layer_dims[l], layer_dims[l-1])
bl -- bias vector of shape (layer_dims[l], 1)
"""
np.random.seed(3)
parameters = {}
L = len(layer_dims) # number of layers in the network
for l in range(1, L):
### START CODE HERE ### (≈ 2 lines of code)
parameters['W' + str(l)] = np.random.randn(layer_dims[l], layer_dims[l-1])*0.01
parameters['b' + str(l)] = np.zeros((layer_dims[l], 1))
### END CODE HERE ###
assert(parameters['W' + str(l)].shape == (layer_dims[l], layer_dims[l-1]))
assert(parameters['b' + str(l)].shape == (layer_dims[l], 1))
return parameters코드는 위와 같이 구현할 수 있습니다. 매개변수로 받는 layer_dim은 각 layer의 크기를 담고 있는 list입니다.
만약, layer_dim이 [5,4,3]으로 주어진다면,
- W1 = (4, 5)
- b1 = (4, 1)
- W2 = (3, 4)
- b2 = (3, 1)
로 파라미터의 차원이 결정됩니다. layer_dim의 맨 처음 요소는 input layer의 크기 \(n^{[0]}\) 입니다.
4. Forward propagation module
4.1 Linear Forward
파라미터를 초기화했고, 다음으로 FP를 진행해야 합니다.
순서대로 다음의 3개의 값을 계산하는 함수를 만들어봅시다.
1. Linear
2. Linear -> activation (activation은 ReLU 또는 Sigmoid임)
3. [Linear -> ReLU] x (L-1) -> Linear -> Sigmoid (FP 전체과정)
Linear Forward는 다음과 같이 구할 수 있습니다.
\[Z^{[l]} = W^{[l]}A^{[l-1]} + b^{[l]}\]
여기서 \(A^{[0]} = X\) 입니다.
# GRADED FUNCTION: linear_forward
def linear_forward(A, W, b):
"""
Implement the linear part of a layer's forward propagation.
Arguments:
A -- activations from previous layer (or input data): (size of previous layer, number of examples)
W -- weights matrix: numpy array of shape (size of current layer, size of previous layer)
b -- bias vector, numpy array of shape (size of the current layer, 1)
Returns:
Z -- the input of the activation function, also called pre-activation parameter
cache -- a python tuple containing "A", "W" and "b" ; stored for computing the backward pass efficiently
"""
### START CODE HERE ### (≈ 1 line of code)
Z = np.dot(W, A) + b
### END CODE HERE ###
assert(Z.shape == (W.shape[0], A.shape[1]))
cache = (A, W, b)
return Z, cache
4.2 Linear-Activation Forward
activation 계산에 두 가지 종류의 함수 Sigmoid와 ReLU가 사용됩니다.
- Sigmoid: \(\sigma(Z) = \sigma(WA + b) = \frac{1}{1 + e^{-(WA + b)}}\)로 계산되고, 이 함수는 Activation 값과 Z를 포함하는 cache를 반환합니다(cache는 BP에서 재사용됩니다).
A, activation_cache = sigmoid(Z)
- ReLU : \(A = RELU(Z) = max(0, Z)\) 로 계산됩니다. 마찬가지로 Activation값과 cache를 반환합니다.
A, activation_cache = relu(Z)
중간의 hidden layer는 ReLU로 계산해야되고, 마지막 ouput layer는 sigmoid로 계산해야되기 때문에, 어떤 함수가 사용되는지 알려주는 역할을 하는 activation을 매개변수로 입력받습니다.
\[A^{[l]} = g(Z^{[l]}) = g(W^{[l]}A^{[l - 1]} + b^{[l]})\]
# GRADED FUNCTION: linear_activation_forward
def linear_activation_forward(A_prev, W, b, activation):
"""
Implement the forward propagation for the LINEAR->ACTIVATION layer
Arguments:
A_prev -- activations from previous layer (or input data): (size of previous layer, number of examples)
W -- weights matrix: numpy array of shape (size of current layer, size of previous layer)
b -- bias vector, numpy array of shape (size of the current layer, 1)
activation -- the activation to be used in this layer, stored as a text string: "sigmoid" or "relu"
Returns:
A -- the output of the activation function, also called the post-activation value
cache -- a python tuple containing "linear_cache" and "activation_cache";
stored for computing the backward pass efficiently
"""
if activation == "sigmoid":
# Inputs: "A_prev, W, b". Outputs: "A, activation_cache".
### START CODE HERE ### (≈ 2 lines of code)
Z, linear_cache = linear_forward(A_prev, W, b)
A, activation_cache = sigmoid(Z)
### END CODE HERE ###
elif activation == "relu":
# Inputs: "A_prev, W, b". Outputs: "A, activation_cache".
### START CODE HERE ### (≈ 2 lines of code)
Z, linear_cache = linear_forward(A_prev, W, b)
A, activation_cache = relu(Z)
### END CODE HERE ###
assert (A.shape == (W.shape[0], A_prev.shape[1]))
cache = (linear_cache, activation_cache)
return A, cache
4.3 L-layer Model
모든 layer에서의 FP를 진행하기 위한 함수를 구현합니다. 예측값인 AL(\(\hat{Y}\)), 그리고 각 layer의 cache를 저장한 caches를 반환합니다.
[Linear -> ReLU] x (L-1) -> Linear -> Sigmoid
AL 변수는 다음을 의미합니다.
\[A^{[L]} = \sigma(Z^{[L]}) = \sigma(W^{[L]}A^{[L-1]} + b^{[L]}) = \hat{Y}\]
# GRADED FUNCTION: L_model_forward
def L_model_forward(X, parameters):
"""
Implement forward propagation for the [LINEAR->RELU]*(L-1)->LINEAR->SIGMOID computation
Arguments:
X -- data, numpy array of shape (input size, number of examples)
parameters -- output of initialize_parameters_deep()
Returns:
AL -- last post-activation value
caches -- list of caches containing:
every cache of linear_activation_forward() (there are L-1 of them, indexed from 0 to L-1)
"""
caches = []
A = X
L = len(parameters) // 2 # number of layers in the neural network
# Implement [LINEAR -> RELU]*(L-1). Add "cache" to the "caches" list.
for l in range(1, L):
A_prev = A
### START CODE HERE ### (≈ 2 lines of code)
A, cache = linear_activation_forward(A_prev, parameters['W'+str(l)], parameters['b'+str(l)], activation = "relu")
caches.append(cache)
### END CODE HERE ###
# Implement LINEAR -> SIGMOID. Add "cache" to the "caches" list.
### START CODE HERE ### (≈ 2 lines of code)
AL, cache = linear_activation_forward(A, parameters['W'+str(L)], parameters['b'+str(L)], activation = "sigmoid")
caches.append(cache)
### END CODE HERE ###
assert(AL.shape == (1,X.shape[1]))
return AL, caches
5. Cost Function
Cost J를 계산하는 함수입니다. 아래의 식으로 계산됩니다.
\[J = -\frac{1}{m}\sum_{i = 1}^{m}(y^{(i)}log(a^{[L](i)}) + (1 - y^{(i)})log(1 - a^{[L](i)}))\]
# GRADED FUNCTION: compute_cost
def compute_cost(AL, Y):
"""
Implement the cost function defined by equation (7).
Arguments:
AL -- probability vector corresponding to your label predictions, shape (1, number of examples)
Y -- true "label" vector (for example: containing 0 if non-cat, 1 if cat), shape (1, number of examples)
Returns:
cost -- cross-entropy cost
"""
m = Y.shape[1]
# Compute loss from aL and y.
### START CODE HERE ### (≈ 1 lines of code)
cost = (-1 / m) * np.sum(Y * np.log(AL) + (1 - Y) * np.log(1 - AL), axis = 1)
### END CODE HERE ###
cost = np.squeeze(cost) # To make sure your cost's shape is what we expect (e.g. this turns [[17]] into 17).
assert(cost.shape == ())
return cost
6. Backward propagation module
FP에서 구한 결과를 사용해서 BP를 진행해서 Cost Function의 gradient를 구합니다.
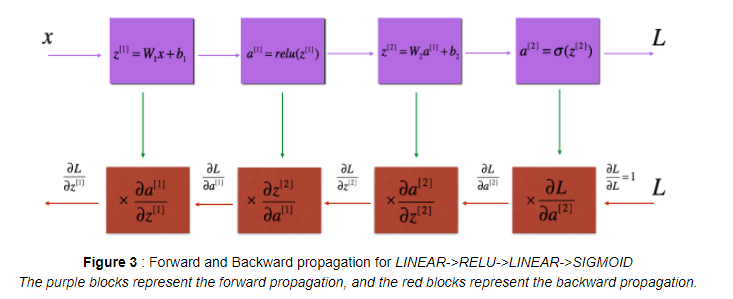
FP와 마찬가지로 3단계의 BP 함수를 구현해봅시다.
1. Linear backward
2. Linear->Activation backward(마찬가지로 activation은 sigmoid와 ReLU 두 가지입니다.)
3. [Linear -> ReLU] x (L-1) -> Linear -> Sigmoid backward(전체 BP 모델)
6-1 Linear backward
하나의 layer \(l\)에서, linear part는 \(Z^{[l]} = W^{[l]}A^{l -1} + b^{[l]}\) 입니다.
이 함수에서는 이미 계산된 미분항 \(dZ^{[l]} = \frac{\partial \mathscr{L}}{\partial Z^{[l]}}\)를 가지고, \((dW^{[l]}, db^{[l]}, dA^{[l-1]})\)를 구합니다.

output은 다음과 같이 계산됩니다.
\[\begin{matrix} dW^{[l]} = \frac{\partial \mathscr{J}}{\partial W^{[l]}} = \frac{1}{m}dZ^{[l]}A^{[l-1]T} \\ db^{[l]} = \frac{\partial \mathscr{J}}{\partial b^{[l]}} = \frac{1}{m}\sum_{i = 1}^{m}dZ^{[l](i)} \\ dA^{[l-1]} = \frac{\partial \mathscr{J}}{\partial A^{[l-1]}} = W^{[l]T}dZ^{[l]} \end{matrix}\]
# GRADED FUNCTION: linear_backward
def linear_backward(dZ, cache):
"""
Implement the linear portion of backward propagation for a single layer (layer l)
Arguments:
dZ -- Gradient of the cost with respect to the linear output (of current layer l)
cache -- tuple of values (A_prev, W, b) coming from the forward propagation in the current layer
Returns:
dA_prev -- Gradient of the cost with respect to the activation (of the previous layer l-1), same shape as A_prev
dW -- Gradient of the cost with respect to W (current layer l), same shape as W
db -- Gradient of the cost with respect to b (current layer l), same shape as b
"""
A_prev, W, b = cache
m = A_prev.shape[1]
### START CODE HERE ### (≈ 3 lines of code)
dW = (1/m)*np.dot(dZ, A_prev.T)
db = (1/m)*np.sum(dZ, axis = 1, keepdims = True)
dA_prev = np.dot(W.T, dZ)
### END CODE HERE ###
assert (dA_prev.shape == A_prev.shape)
assert (dW.shape == W.shape)
assert (db.shape == b.shape)
return dA_prev, dW, db
6.2 Linear-Activation backward
6.1 함수를 수행하기 전 dZ를 구하고, 6.1 함수를 수행하는 linear-activation backward 함수를 구현합니다.
여기서 제공되는 sigmoid_backward와 relu_backward 함수를 사용해서 dZ를 구하게 됩니다.
\(g(z)\)는 activation 함수, \({g(z)}'\)는 activation의 도함수입니다.
\[dZ^{[l]} = dA^{[l]} \ast {g}'(Z^{[l]})\]
# GRADED FUNCTION: linear_activation_backward
def linear_activation_backward(dA, cache, activation):
"""
Implement the backward propagation for the LINEAR->ACTIVATION layer.
Arguments:
dA -- post-activation gradient for current layer l
cache -- tuple of values (linear_cache, activation_cache) we store for computing backward propagation efficiently
activation -- the activation to be used in this layer, stored as a text string: "sigmoid" or "relu"
Returns:
dA_prev -- Gradient of the cost with respect to the activation (of the previous layer l-1), same shape as A_prev
dW -- Gradient of the cost with respect to W (current layer l), same shape as W
db -- Gradient of the cost with respect to b (current layer l), same shape as b
"""
linear_cache, activation_cache = cache
if activation == "relu":
### START CODE HERE ### (≈ 2 lines of code)
dZ = relu_backward(dA, activation_cache)
dA_prev, dW, db = linear_backward(dZ, linear_cache)
### END CODE HERE ###
elif activation == "sigmoid":
### START CODE HERE ### (≈ 2 lines of code)
dZ = sigmoid_backward(dA, activation_cache)
dA_prev, dW, db = linear_backward(dZ, linear_cache)
### END CODE HERE ###
return dA_prev, dW, db
6.3 L-model Backward
이제, 전체 network에서의 backward 함수를 구현합니다. L_model_forward 함수를 통해서, 매 iteration마다 (X, W, b, z)를 저장한 cache를 기억하면서, BP module에서 cache를 사용해 gradient를 계산합니다.

Initializing backpropagation: 신경망에서 BP를 진행하기 위해서는 우선 BP 입력값인 dAL을 계산해야 합니다.
dAL = \(\frac{\partial \mathscr{L}}{\partial A^{[L]}}\)은 다음과 같이 계산됩니다.
dAL = - (np.divide(Y, AL) - np.divide(1 - Y, 1 - AL))
즉, 다음을 계산한 것입니다.
\[-(\frac{Y}{AL} - \frac{(1 - Y)}{(1 - AL)})\]
계산된 미분값은 grads에 저장되며, \(l = 3\)인 경우에 \(dW^{[l]}, db^{[l]}\)는 grads["dW3"], grads["db3"]에 저장됩니다.
# GRADED FUNCTION: L_model_backward
def L_model_backward(AL, Y, caches):
"""
Implement the backward propagation for the [LINEAR->RELU] * (L-1) -> LINEAR -> SIGMOID group
Arguments:
AL -- probability vector, output of the forward propagation (L_model_forward())
Y -- true "label" vector (containing 0 if non-cat, 1 if cat)
caches -- list of caches containing:
every cache of linear_activation_forward() with "relu" (it's caches[l], for l in range(L-1) i.e l = 0...L-2)
the cache of linear_activation_forward() with "sigmoid" (it's caches[L-1])
Returns:
grads -- A dictionary with the gradients
grads["dA" + str(l)] = ...
grads["dW" + str(l)] = ...
grads["db" + str(l)] = ...
"""
grads = {}
L = len(caches) # the number of layers
m = AL.shape[1]
Y = Y.reshape(AL.shape) # after this line, Y is the same shape as AL
# Initializing the backpropagation
### START CODE HERE ### (1 line of code)
dAL = -(np.divide(Y, AL) - np.divide(1 - Y, 1 - AL))
### END CODE HERE ###
# Lth layer (SIGMOID -> LINEAR) gradients. Inputs: "dAL, current_cache". Outputs: "grads["dAL-1"], grads["dWL"], grads["dbL"]
### START CODE HERE ### (approx. 2 lines)
current_cache = caches[L-1]
grads["dA" + str(L-1)], grads["dW" + str(L)], grads["db" + str(L)] = linear_activation_backward(dAL, current_cache, activation = "sigmoid")
### END CODE HERE ###
# Loop from l=L-2 to l=0
for l in reversed(range(L-1)):
# lth layer: (RELU -> LINEAR) gradients.
# Inputs: "grads["dA" + str(l + 1)], current_cache". Outputs: "grads["dA" + str(l)] , grads["dW" + str(l + 1)] , grads["db" + str(l + 1)]
### START CODE HERE ### (approx. 5 lines)
current_cache = caches[l]
dA_prev_temp, dW_temp, db_temp = linear_activation_backward(grads["dA"+str(l+1)], current_cache, activation = "relu")
grads["dA" + str(l)] = dA_prev_temp
grads["dW" + str(l + 1)] = dW_temp
grads["db" + str(l + 1)] = db_temp
### END CODE HERE ###
return grads
6.4 Update Parameters
BP를 진행해 gradient를 구하고 gradient descent를 사용해 파라미터를 업데이트합니다.
\[\begin{matrix} W^{[l]} = W^{[l]} - \alpha dW^{[l]} \\ b^{[l]} = b^{[l]} - \alpha db^{[l]} \end{matrix}\]
위와 같이 갱신되며, \(\alpha\)는 learning rate입니다. 업데이트된 파라미터값은 parameters에 저정됩니다.
# GRADED FUNCTION: update_parameters
def update_parameters(parameters, grads, learning_rate):
"""
Update parameters using gradient descent
Arguments:
parameters -- python dictionary containing your parameters
grads -- python dictionary containing your gradients, output of L_model_backward
Returns:
parameters -- python dictionary containing your updated parameters
parameters["W" + str(l)] = ...
parameters["b" + str(l)] = ...
"""
L = len(parameters) // 2 # number of layers in the neural network
# Update rule for each parameter. Use a for loop.
### START CODE HERE ### (≈ 3 lines of code)
for l in range(L):
parameters["W" + str(l+1)] = parameters["W" + str(l+1)] - learning_rate * grads["dW" + str(l + 1)]
parameters["b" + str(l+1)] = parameters["b" + str(l+1)] - learning_rate * grads["db" + str(l + 1)]
### END CODE HERE ###
return parameters
NN의 구성을 단계별로 구현해보았습니다. 다음 실습에서 이 함수들을 사용해서 2주차 실습에 Logistic Regression으로 구현한 cat vs non-cat 분류기를 NN으로 구현해보도록 하겠습니다.
'Coursera 강의 > Deep Learning' 카테고리의 다른 글
| [실습] Initialization 초기화 (0) | 2020.09.26 |
|---|---|
| [실습] Deep Neural Network for Image Classification(cat vs non-cat) (6) | 2020.09.26 |
| [실습] Planar data classification with a hidden layer (9) | 2020.09.25 |
| [실습] Logistic Regression with a Neural Network(can / non-cat classifier) (0) | 2020.09.24 |
| Practical aspects of Deep Learning 2 (3) | 2020.09.23 |




댓글