해당 내용은 Andrew Ng 교수님의 Machine Learning 강의(Coursera)를 정리한 내용입니다.
이번에는 Anomaly Detection(이상탐지)에 대해서 이야기해볼 것이다.
Anomaly Detection은 머신러닝에서 일반적이며, 합리적으로 사용된다. 그리고 이것은 주로 unsupervised problem의 한 방법이지만, superivsed learning problem의 측면도 가지고 있다.
아래 예시를 통해서 Anomaly Detection이 무엇인지 살펴보도록 하자.
- Density Estimation

여기 항공기 엔진 제조업체가 있고, 항공기 엔진을 조립이 완료되었을 때, 품질을 테스트한다고 가정해보자.
그 테스트 중에 우리는 항공기 엔진의 기능을 측정하는데, 예를 들어서 엔진에 생성된 열, 진동 등을 측정한다. \(x_1, x_2, ..., x_m\)의 feature를 가질 수 있지만, 열과 진동, 두 개의 feature를 가지고 이야기를 해보겠다.
기존에 학습된 데이터 결과를 바탕으로 새로운 엔진 \(x_{test}\)가 있을 때, 테스트 샘플의 각 feature가 평균에 가까이 위치하면 정상적인 엔진으로 판단할 수 있고, 만약 학습된 데이터와는 다르게(평균과 다르게) 위치한다면 이상하다고 볼 수 있을 것이다.

이처럼 Density Estimation은 우리가 테스트한 샘플이 feature에 대해서 정상적일 확률 \(p(x)\)을 계산해서 판단하는 것이다. 만약 학습 데이터가 많이 존재하는 곳에 위치한다면 확률이 높을 것이고, 학습 데이터와 많이 떨어져 있다면 확률이 낮을 것이다.
우리는 아래와 같이 판단을 해서 정상/이상을 판단하게 된다.
\[\begin{align*} p(x_{test}) &< \epsilon \rightarrow \text{ anomaly} \\ p(x_{test}) &\geq \epsilon \rightarrow \text{ OK} \end{align*}\]
이 방법은 다음과 같은 이상탐지에 사용될 수 있다.

사용자의 행동을 각 feature로 두고 정상 확률 \(p(x)\)를 학습한 후에, 사기인지 확인하는 데에 사용될 수 있고, 제조업에서 정상적으로 제품이 완성됬는지에도 사용된다.
또한, 데이터 센터에서 위와 같은 feature로 컴퓨터들을 모니터링할 때, 어느 feature 중에 하나가 \(p(x) < \epsilon\)이라면 그 컴퓨터는 비정상이라고 판단할 수 있다.
[Gaussian(Normal) Distribution]
가우시안 분포에 대해서 먼저 알아보자.
가우시안 분포는 정규분포(Normal Distribution)이라고 불린다.
만약 \(x \in \mathbb{R}\)일 때, x가 평균(mean) \(\mu\), 분산(variance) \(\sigma^2\)인 가우시안 분포를 따른다고 했을 때 우리는 다음과 같이 표현한다. 여기서 \(\sigma\)는 표준편차(standard deviation)이다.
\[x \sim N(\mu, \sigma^2)\]
이 그래프는 아래와 같이 나타낼 수 있다.

그리고 \(p(x; \mu, \sigma^2)\), x의 확률은 다음 공식으로 구할 수 있다.
\[p(x; \mu, \sigma^2) = \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x - \mu)^2}{2\sigma^2}}\]
\(\mu\)와 \(\sigma^2\)에 따라서 다음과 같은 그래프 모양의 분포를 가지며, 그래프 곡선의 면적은 1이다. 분산이 커질수록 그래프가 더 넓게 퍼지게 되고, 평균은 그래프의 중심을 이동시키는 축이 된다.
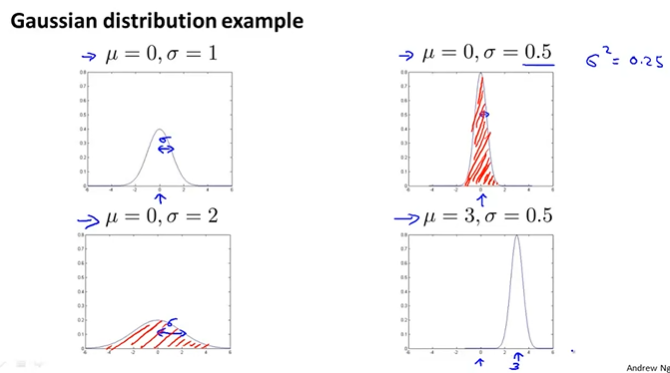
이제 다시 돌아와서, 우리의 머신러닝에 어떻게 적용하는 지 살펴보자.
\(x^{(1)}, x^{(2)}, ... x^{(m)}, x \in \mathbb{R}\)의 Dataset이 있을 때, 우리는 example \(x^{(i)}\)에 대해서 다음과 같이 그래프 분포를 구할 수 있다.
\[x^{(i)} \sim N(\mu, \sigma^2)\]

example \(x^{(i)}\)의 대한 평균과 분산은 위와 같이 구할 수 있다.
[Algorithm]
\(p(x)\)를 구하는 알고리즘은 다음과 같이, 모든 feature에 대한 \(p(x_i; \mu_i, \sigma_i^2)\)을 구해서 모두 곱해주면 된다.
\[\begin{align*} p(x) &= p(x_1; \mu_1, \sigma_1^2)p(x_2; \mu_2, \sigma_2^2) \cdots p(x_n; \mu_n, \sigma_n^2) \\ &= \prod_{j = 1}^{n}p(x_j; \mu_j, \sigma_j^2) \end{align*}\]
으로 구할 수 있고, 각 feature는 다음을 따르는 가우시안 분포를 가진다. 여기서 \(\prod\)는 모든 항의 곱을 의미한다.
\[\begin{matrix} x_1 \sim N(\mu_1, \sigma_1^2) \\ x_2 \sim N(\mu_2, \sigma_2^2) \\ \cdots \\ x_n \sim N(\mu_n, \sigma_n^2)\end{matrix}\]
알고리즘을 정리하면 다음과 같다.

1. 비정상 데이터를 찾기위한 feature를 선택한다.
2. 각 feature의 평균과 분산을 구한다.
3. 새로운 샘플 x에 대해서 \(p(x)\)를 구한다. 만약 특정 값 \(\epsilon\)보다 작다면 이상이 있는 것이다.
여기서 j는 feature의 index를 의미한다.
아래 예시에서는 학습된 \(p(x)\)에 대해서 \(\epsilon\)을 0.02로 설정하고 새로운 샘플 \(x_{test}^{(1)}, x_{test}^{(2)}\)의 \(p(x)\)를 구했을 때, \(x_{test}^{(1)}\)은 0.02보다 커서 정상이고, \(x_{test}^{(2)}\)는 0.02보다 작기 때문에 이상이 있다고 추측할 수 있다.

- Building an Anomaly Detection System
이번에는 이상감지 알고리즘(시스템)을 어떻게 구성하고 평가하는지에 대해서 알아보자.

우선 이전 강의에서 언급했듯이 숫자로 평가 지표를 나타낼 수 있는게 중요하다. 이렇게 우리가 학습 알고리즘을 평가하는 방법이 있다면 우리가 머신러닝을 개발할 때 feature를 선택하는 등의 의사 결정에서 더욱 쉽게 결정할 수 있다.
우리에게 정상/비정상으로 분류된 데이터가 있다고 하자(y = 0이면 정상, y = 1이면 비정상).
그리고 그 데이터를 우리는 Training Set, Cross Validation Set, Test Set으로 나누어서 \(p(x)\)를 학습하고 제대로 학습이 되었는지 CV Set과 Test Set으로 평가하는 방법을 사용할 것이다.

항공기 엔진 예시로 돌아가서, 우리에게 10000개의 정상 엔진과 20개의 비정상 엔진이 있다고 한다면, 우리는 위와 같이 Training Set에는 6000개의 정상 엔진, CV Set에는 2000개의 정상 엔진과 10개의 비정상 엔진, 그리고 Test Set에는 나머지 2000개의 정상 엔진과 10개의 비정상 엔진으로 나눌 수 있다. (Training : 60%, CV : 20%, Test 20%)
여기서 비정상 엔진은 CV Set과 Test Set에만 분배하였다.
이렇게 나누어서 Training Set으로 \(p(x)\)를 학습하고, CV Set과 Test Set으로 검증하고 평가할 수 있을 것이다.
다른 방법으로는 Training Set은 동일하게 6000개의 정상엔진, 그리고 나머지 4000개의 정상엔진은 CV Set과 Test Set에 동일하게 사용하는 경우도 있는데, 이 경우는 권장하지는 않는다.

그리고 알고리즘의 평가는 다음과 같이 이루어질 수 있을 것이다.

1. Training Set으로 model \(p(x)\)를 학습한다.
2. CV Set과 Test Set으로 예측결과를 얻는다.
\[y = \left \{ \begin{matrix} 1 & \text{if } p(x) < \epsilon \text{ (anomaly)} \\ 0 & \text{if } p(x) \geq \epsilon \text{ (normal)} \end{matrix} \right. \]
자세히 살펴보면 supervised learning과 매우 유사한 것을 볼 수 있다.
(참조 : 2020/08/20 - [ML and DL/Machine Learning] - [Machine Learning] Machine Learning System Design)
그리고 보통 정상적인 경우가 대부분이고 비정상인 경우는 매우 적기 때문에 skewed data일 수가 있다. 따라서 우리는 다음과 같은 방법으로 평가할 수 있다.

마지막으로 매개변수 \(\epsilon\)이 있는데, 이 \(\epsilon\)값은 정상과 비정상을 나누는 임계값(Threshold)이다.
우리는 CV Set를 매개변수 \(\epsilon\)을 바꾸어 가면서 테스트해서 \(F_1\)점수를 최대화하는 \(\epsilon\)값을 선택할 수 있을 것이다.
[Anomaly detection vs. supervised learning]
결국 Anomaly detection은 y = 0 or 1의 class로 분류하는 binary classification으로 볼 수 있고, supervised learning인 logistic regression이나 NN을 사용할 수도 있는 것처럼 보인다. 하지만 왜 사용하지 않는지, 즉, 언제 anomaly detection algorithm을 사용해야하는 지와 supervised learning을 사용하는 대신 얼마나 더 효과가 있는지에 대해서 알아보자.

Anomaly detection의 경우에는 데이터에서 y = 0인 정상인 데이터가 매우 많고, 그에 비해서 비정상인 데이터(y = 1)는 매우 적을 경우에 사용하면 좋다. 그리고 Supervised Learning이나 NN의 경우에는 비정상 라벨을 가진 경우에도 일정한 규칙이나 형식을 찾을 수 있지만, 엔진 평가에서 어떠한 비정상 값이 나올지 예측이 되지 않는 경우에는 Anomaly Detection을 사용하는 것이 유용하다(완전히 새로운 비정상 데이터가 나올 수 있다). 즉, Supervised Learning에서는 충분한 positive example에 대해서 학습을 하고, 나중에 positive example이 들어오더라도 기존의 것과 유사할 것이지만, 전혀 기존의 것과 다른 것이 나온다면 positive로 판단하지 않을 것이다.
아래는 Anomaly Detection과 Supervised Learning이 사용되는 곳이다.

이렇게 나누어질 수 있지만, 만약 Fraud detection에서 y = 1인 example이 많다면 supervised learning으로도 학습이 가능하다(실제로 그런 경우가 있음).
[Choosing What Features to Use]
앞서 Anomaly Detection 알고리즘을 살펴봤고, 어떻게 평가하는지 알아보았다.
Anomaly Detection 알고리즘을 적용할 때, 알고리즘이 얼마나 잘 동작하느냐에 영향을 미치는 가장 큰 부분은 이 알고리즘에 어떠한 feature를 사용하느냐이다. 이번 시간에는 feature를 디자인하거나 선택하는데 필요한 가이드라인을 살펴보자.
Non-gaussian features
Anomaly Detection 알고리즘을 적용할 때 확인해보는 것 중의 하나가 선택한 feature의 히스토그램을 그려서 그래프가 가우시안 분포를 따르는 지 확인하는 것이다.
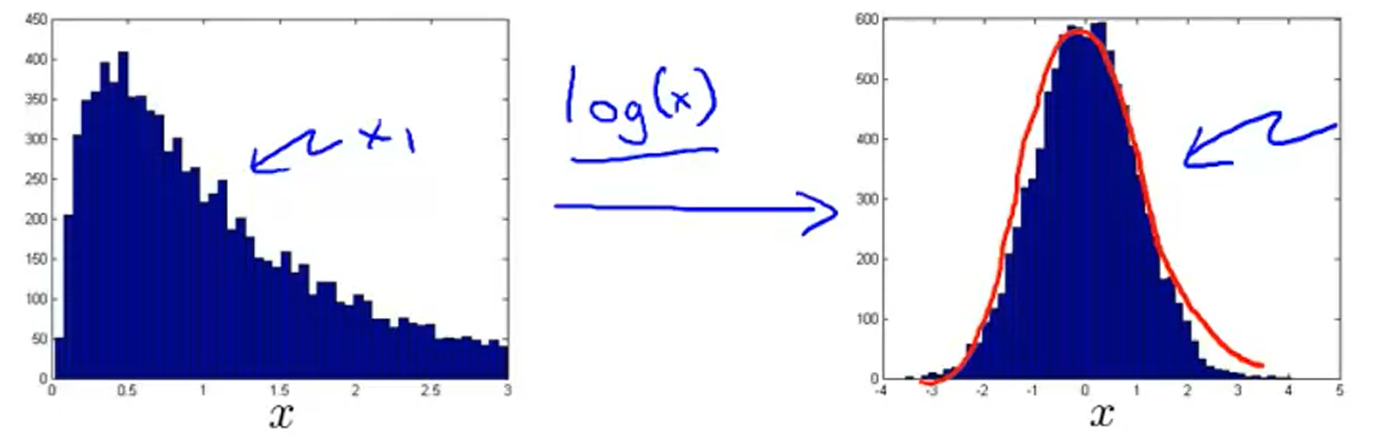
만약 왼쪽처럼 히스토그램이 가우시안 분포가 아닌 이상한 분포를 보인다면 여기서는 log를 취해서 가우시안 분포와 유사하게 만들어 줄 수 있다.
이처럼 Non-gaussian feature를 사용할 때에는 Transformation을 통해서 가우시안 분포를 따르도록 바꿔주면 된다. 위의 예시처럼 log를 취해도 되고, polynomial을 사용해도 된다.
Error analysis for anomaly detection
이상적인 Anomaly Detection에서는 정상 example에 대해서는 \(p(x)\)가 크고, 비정상 example에 대해서는 \(p(x)\)가 작아야 한다.
하지만 실제 대부분의 문제는 정상 example과 비정상 example의 \(p(x)\)가 비슷해서 발생한다. 즉, 둘 다 충분히 큰 경우가 발생하는 것이다. 이런 경우에는 비정상의 \(p(x)\)도 꽤나 큰 확률을 가지기 때문에 새로운 feature를 추가하는 방법을 시도해야 한다.
아래 그래프처럼 하나의 feature로는 비정상의 확률이 꽤 크게 나오기 때문에 feature \(x_2\)를 추가해서 분리가 되도록 한다.

Monitoring computers in a data center
여러 feature들 중에서 선택해야 할 때에는 비정상적인 상황이 발생했을때, 비정상적으로 크거나 작은 값을 가지는 feature들을 선택하는 것이 좋다.
data center에서는 다음과 같이 선택하거나 새로운 feature를 추가할 수도 있다.

- Multivariate Gaussian Distribution

위 그래프에 \(x_1, x_2\) feature가 있고, 그 feature들의 정규분포는 오른쪽과 같이 나타난다. 우리가 비정상 값으로 왼쪽위 \(x_1 = 0.4, x_2 = 1.5\) 지점의 가우시안 분포의 확률을 본다면, 이 값은 전혀 비정상처럼 보이지 않는다. 따라서 anomaly detection 알고리즘이 \(x_1 = 0.4, x_2 = 1.5\) 지점이 비정상이라고 판단하지 못하게 된다. 즉, 파란색 타원은 확률영역을 제대로 보여주지 못하고 있고, 분홍색 원과 같이 확률이 분포할 것으로 예측된다.
이 문제를 해결하기 위해서 Multivariate Gaussian (Normal) distribution을 사용할 수 있다.

파라미터 \(\mu\)(\(\in \mathbb{R}^n\))와 \(\Sigma\)(\(\mathbb{R}^{n \times n}\))를 사용해서, 정규분포 곡선을 변형할 수 있다. 여기서 \(\Sigma\)는 PCA에서 살펴보았던 covariance matrix이다.
(아마 PCA와 유사한 방법으로 정규분포 곡선의 모양을 변형시키는 것 같다)
여기서 \(p(x)\)는 한번에 구하게 된다.

Anomaly detection with the multivariate Gaussian
Multivariate Gaussian을 적용한 Anomaly Detection 알고리즘은 다음과 같다.
1. Fit model \(p(x)\) by setting
\(\begin{align*} &\mu = \frac{1}{m}\sum_{i = 1}^{m}x^{(i)} \\ &\Sigma = \frac{1}{m}\sum_{i = 1}^{m}(x^{(i)} - \mu)(x^{(i)} - \mu)^T \end{align*}\)
2. Given a new example \(x\), compute
\[p(x) = \frac{1}{(2\pi)^{\frac{n}{2}}\left | \Sigma \right |^{\frac{1}{2}}}exp(-\frac{1}{2}(x - \mu)^T\Sigma^{-1}(x - \mu))\]
2번의 계산 결과가 \(p(x) < \epsilon\)이라면 비정상이다.
원래 모델과 비교를 해보자.


기존 모델은 수동으로 feature를 추가해야하는 경우가 있지만, Multivariate Gaussian은 feature들간의 관계가 자동으로 도출된다. 또한 기존 모델은 연산이 작고, trainint set의 개수가 적어도 괜찮다. 반면에, multivariate gaussian은 연산 비용이 크고, 반드시 m > n이어야 한다(\(\Sigma\)가 n x n차원이기 때문). 그렇지 않으면 Covariance Matrix가 비가역적, 즉 역행렬이 존재하지 않을 수 있어서 이 알고리즘을 사용할 수 없다. m >= 10n 일 때, 사용을 권장한다.
'Coursera 강의 > Machine Learning' 카테고리의 다른 글
| [Machine Learning] Exam 8 (Week 9) (0) | 2020.09.04 |
|---|---|
| [Machine Learning] Recommender Systems (0) | 2020.09.04 |
| [Machine Learning] Exam 7 (Week 8) (0) | 2020.08.27 |
| [Machine Learning] Dimensionality Reduction(PCA) (1) | 2020.08.27 |
| [Machine Learning] Unsupervised Learning 비지도 학습 (0) | 2020.08.25 |




댓글