해당 내용은 Andrew Ng 교수님의 Machine Learning 강의(Coursera)를 정리한 내용입니다.
- Recommender System
이번 시간에는 현업에서 많이 주목받고 사용되는 추천시스템에 대해서 알아보자.
다음과 같은 영화 별점을 예측하는 예제를 살펴보자. 사용자들은 별점 0개에서 5개까지 사용해서 영화를 평가한다.
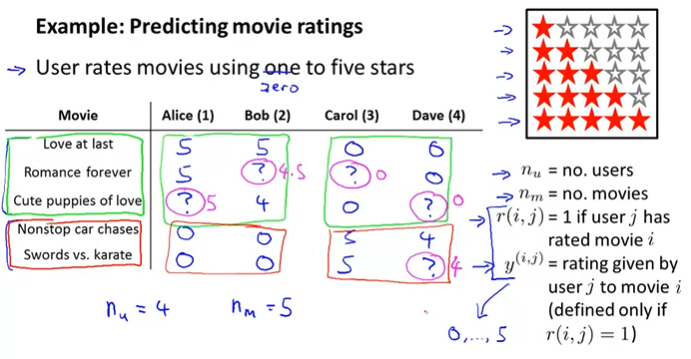
그리고 아래 4개의 parameter를 사용한다.
- \(n_u\) = 유저의 수
- \(n_m\) = 영화의 개수
- \(r(i, j)\) = j 유저가 영화 i를 평가했는지에 대한 여부. 평가했으면 1, 안했으면 0이다.
- \(y^{(i, j)}\) = j 유저가 영화 i에 평가한 별점이다. 0 ~ 5까지의 값을 가지며, 이 값은 \(r(i, j)\) = 1 일 때만 정의된다.
위 예시에서는 5개의 영화와 4명의 유저가 있다. 그리고 초록색 박스 안의 영화는 로맨틱영화이고 빨간 박스 안의 영화는 액션영화이다. 여기서 Alice와 Bob은 로맨틱영화에 많은 점수를 줬고, 액션영화에는 점수는 낮게 주었다. 반대로 Carol과 Dave는 액션영화에 높은 점수를 주고, 로맨틱영화에 낮은 점수를 주었다. 이런 상황에서 우리는 ?에 해당하는 점수를 예측해보자. 직관적으로 Alice와 Bob은 로맨틱영화에 더 높은 점수를 주었으므로, 로맨틱영화에는 높은 점수를 주고, 액션영화에는 낮은 점수를 주었을 가능성이 높다. Carol과 Dave는 반대일 것이다.
이때, Recommander System을 사용하면 이 값들을 예측할 수 있다. 아마존이나 넷플릭스, 아이튠즈에서 이러한 시스템을 사용할 것이다.
[Content Based Recommendations]
이러한 추천 시스템에서 사용할 수 있는 방법 중 하나인 Content Based Recommendation(CBR)에 대해서 알아보자.

위와 같은 정보가 있을 때, 우리는 어떻게 ?에 대한 점수를 계산할 수 있을까?
계산을 하기 위해서 우리는 아래와 같은 feature \(x_1, x_2\)를 사용해 볼 것이다.
\(x_1\)은 영화의 로맨틱 정도(degree)이고, \(x_2\)는 영화의 액션 정도이다.
여기서 Love at last는 로맨틱 정도가 0.9이고 액션 정도는 0으로 나타나고 있다. 거의 액션이 없다고 보면 될 것 같다. 반대로 Swords vs. karate는 로맨틱 정도가 0이고 액션 정도가 0.9로 나타난다. 아마 로맨스보다는 액션이 주가 되는 영화일 것이다.
이렇게 feature를 가지고 있을 때, 우리는 각 영화에 대해서 각 feature에 해당하는 값을 벡터로 나타낼 수 있다. 영화를 위에서 순서대로 1~5의 번호를 주고, bias feature(interceptor)인 \(x_0 = 1\)을 포함해서, 1번 영화 Love at last \(x^{(1)})\)에 대해서 아래와 같이 나타낼 수 있다.(나머지는 \(x^{(2)}, x^{(3)}, x^{(4)}, x^{(5)}\)가 된다)
\[x^{(1)} = \begin{bmatrix} 1 \\ 0.9 \\ 0 \end{bmatrix}\]
별점을 예측하기 위해서, 우리는 각 유저에 대해서 linear regression를 사용해보자.
그러면 우리는 각 유저 j에 대해서 \(\theta^{(j)} \in \mathbb{R}^{3}\)을 학습하고, 유저 j가 영화 i에 대해서 평가한 값은 \((\theta^{(j)})^T x{(i)}\)라고 예측할 수 있다. (만약 n개의 feature가 있다면 parameter \(\theta\)는 \(\mathbb{R}^{n + 1}\)이다)
구체적인 예시를 들어보면, \(x^{(3)} = \begin{bmatrix} 1 \\ 0.9 \\ 0 \end{bmatrix}\)이고, \(\theta^{(1)} = \begin{bmatrix} 0 \\ 5 \\ 0 \end{bmatrix}\)라면 우리는 다음과 같이 Alice가 Cute puppies of love의 평가를 계산할 수 있다.
\[(\theta^{(i)})^T x^{(3)} = 5 \times 0.99 = 4.95\]
j가 3인 Carol은 액션영화에 높은 점수를 주었으므로, \(\theta^{(3)} = \begin{bmatrix} 0 \\ 0 \\ 5 \end{bmatrix}\) 처럼 될 것이다.
일반화시켜 정리하면 다음과 같다.

그리고 우리는 \(\theta^{(j)}\)를 학습하기 위해서 다음과 같은 식을 계산하면 된다.

Linear Regression의 비용 함수와 유사하지만 크기 \(m\)으로 나누어 주는 부분이 삭제되었다.
그리고 최적의 \(\theta\)값을 구하기 위해서 Gradient Descent를 적용해서 계산한다. \(\alpha\)는 Learning Rate이다.

마찬가지로 Linear Regression에서의 Gradient Descent와 매우 유사하지만 여기서도 \(m\) term이 제거되었다.
\(\alpha\)다음에 나오는 식은 \(\frac{\partial}{\partial \theta_k^{(j)}}J(\theta^{(1)}, ..., \theta^{(n_u)})\)이다.
[Collaborative Filtering]
이번에는 Collaborative Filtering(CF)라는 접근 방법을 알아보자. 이 알고리즘은 feature learning이라 불리는 어떤 feature를 사용해야되는지 스스로 학습하는 특성을 가지고 있다.

좀 전의 예시에서는 위 표와 같이 Data Set이 있고, 각각의 영화에 대해서 얼마나 로맨틱한 영화인지, 액션 영화인지 featrue의 값이 주어졌다고 가정했다. 하지만, 실제로 누군가가 우리에게 각 영화가 얼마나 로맨틱하고 얼마나 액션한지 이 알려주는 것은 매우 시간이 오래 걸리고, 비용 또한 만만치 않을 것이다. 또한, 실제로는 feature가 더욱 많을 것이다.
따라서 이러한 문제점 때문에 아래와 같이 우리는 feature의 값을 모른다고 가정하고 다시 살펴보자.

우리는 사용자로부터 영화의 평점 데이터를 받았지만, 각 영화가 얼마나 로맨틱한지 얼마나 액션스러운지는 확인이 되지 않는다.
따라서, 약간 다른 가정을 해보자.
우리가 유저들에게 접근해서 각 유저들이 로맨틱 영화를 얼마나 좋아하고, 액션 영화를 얼마나 좋아하는 지에 대해서 우리에게 알려주었다고 가정해보겠다. 그 결과 아래와 같이 각 유저에 대한 parameter \(\theta\)를 받았고, 다시말해서 각 유저 j가 자기 자신의 \(\theta^{(j)}\)를 결정하는 것이다.

Alice와 Bob은 로맨틱 영화를 좋아하고, Carol과 Dave는 액션 영화를 좋아하기 때문에 우리는 \(\theta\)를 위와 같이 결정할 수 있게 되었다. \(\theta\)값을 알고 있다면 우리는 반대로 feature \(x_1, x_2\)의 값을 예측할 수 있게 된다. 첫번째 영화 Love at last \(x^{(1)}\)에 대해서 각 유저의 \(\theta^{(j)}\)를 계산해보면 아래와 같이 되며, 따라서 \(x^{(1)}\)의 feature 값은 \(x_1 = 1.0, x_2 = 0.0\)으로 추론이 가능하다.
\[\begin{matrix} (\theta^{(1)})^T x^{(1)} \approx 5 \\ (\theta^{(2)})^T x^{(1)} \approx 5 \\ (\theta^{(3)})^T x^{(1)} \approx 0 \\ (\theta^{(4)})^T x^{(1)} \approx 0 \end{matrix}\]
정리하면 주어진 \(\theta^{(j)}\)에 대해서 \(x^{(i)}\)를 다음과 같이 구할 수 있다.

CBR에서는 \(x^{(i)}\)가 주어졌을 때 최적의 \(\theta^{(j)}\)를 구했지만, 이번에는 \(\theta^{(j)}\)가 주어져있고, 최적의 \(x^{(i)}\)를 구한다. 그래서 비용 함수의 첫 번째항은 동일하지만, 정규화(Regularization)항은 \(\theta\)가 아닌 \(x\)이다.
\(n_m\)개의 영화에 대해서 \(x^{(i)}\)를 계산해야하기 때문에, 최종적으로 아래 공식을 통해서 최적의 \(x^{(i)}\)를 구하게 된다.

그리고 위 식을 최소화하게 모든 영화에 대해서 최적화된 feature 세트를 얻을 수 있다.
그래서 우리가 처음에 다루었던 CBR 알고리즘과 방금 다루었던 알고리즘을 모두 종합해보자.
\(r(i, j)\)와 \(y^{(i. j)}\) 데이터가 주어졌을 때,
CBR 알고리즘은 주어진 \(x^{(i)}\)를 가지고 \(\theta^{(j)}\)를 최적화화는 것이고,
방금 다루었던 알고리즘은 주어진 \(\theta^{(j)}\)를 가지고 \(x^{(i)}\)를 최적화하는 것이다.
조합에 대한 문제는 결국 치킨이 먼저냐 달걀이 먼저냐하는 문제이다.
우리는 우선 \(\theta\)를 랜덤한 값으로 초기화하고 각 알고리즘을 반복하는 방식을 선택할 수 있을 것이다.

이렇게 \(\theta\)와 \(x\)를 반복해서 구하다보면 결국 최적의 \(\theta\)와 \(x\)를 구할 수 있을 것이다.
이 방법이 Collaborative Filtering(CF)의 기본 개념이다. 이것은 parameter와 feature를 어떻게 동시에 학습할 수 있는지에 대한 방향을 알려주고 있다. 이 방법이 실제로 사용할 최종적인 알고리즘은 아니다. 바로 다음 강의에서 이 알고리즘을 어떻게 개선하고 훨씬 더 효율적으로 만드는지 살펴보도록 하자.
그리고 이 추천 시스템 문제의 경우에는 각 유저, 즉 사용자들이 여러 영화를 평가하고 있고, 각 영화들은 사용자에 의해서 평가되었기 때문에 적용이 가능했다. 정리하자면, 이 Collaborative filtering가 수행하는 작업이 모든 사용자들도 도와주고 있는 일종의 공동 작업이다. 알고리즘이 더 좋은 feature들로 학습하기 위해서 사용자들이 돕고 있다는 것이다.
[Collaborative filtering algorithm]
우리는 이전 강의에서 주어진 feature들로 parameter를 학습하는 방법과 주어진 parameter들로 feature를 학습하는 방법에 대해서 알아보았다. 이번에는 두 가지의 방법을 함께 사용하는 Collaborative Filtering Algorithm에 대해서 이야기해보자.

우리는 위와 같은 방법으로 각 feature와 parameter를 구할 수 있었다. 우리는 이 두 개의 최적화 문제를 하나의 식으로 아래와 같이 나타낼 것이다.

이 식은 위의 두 최적화 공식을 하나로 더한 것과 동일하다. Error Term 에서 summation은 \(\sum_{(i,j):r(i,j)=1}\)로 나타나 있는데, 이것은 모든 (i, j) 쌍을 더하라는 의미이다. 즉, (0, 0), (0, 1), ... (0, \(n_u)\)), (1, 0), ..., (\(n_m, n_u\)) 항의 cost를 구하는 것이다. 나머지 항은 regularization 항이다.
위와 같이 우리는 \(x\)와 \(\theta\)에 대해서 비용함수를 하나로 만들었다. 그리고 우리는 아래와 같은 최적화 문제를 계산해서 비용 함수를 최소화하는 \(x\)와 \(\theta\)를 구하면 된다.
\[\underset{\begin{align*} & x^{(1)}, \cdots, x^{(n_m)} \\ & \theta^{(1)}, \cdots, \theta^{(n_u)} \end{align*}}{min}J(x^{(1)}, \cdots, x^{(n_m)}, \theta^{(1)}, \cdots, \theta^{(n_u)})\]
이전 강의의 알고리즘과의 차이점은 \(x\)와 \(\theta\)를 순차적으로 각각 최적화하는 것이 아니라 \(x\)와 \(\theta\)를 한번에 구하고 있다.
그리고 이 방식으로 feature를 학습할 때, 이전에는 interceptor term \(x_0\)을 사용했지만 이것을 제거하도록 한다. 즉, \(x\)는 \(\in \mathbb{R}^n\)을 만족하게 된다. 마찬가지로 parameter \(\theta\)도 동일 차원이기 때문에 더 이상 \(\theta_0\)는 필요하지 않는다.(\(\theta \in \mathbb{R}_n\))
이렇게 bias term을 삭제하는 것은 모든 feature들을 학습하고 있기 때문이다. 따라서 항상 1의 값을 가지는 feature가 필요하면 알고리즘이 자체적으로 \(x_1\)의 값을 1로 설정할 수 있다.
Collaborative Filtering Algorithm은 다음과 같다.

첫 번째로 \(x\)와 \(\theta\)를 작은 랜덤 값으로 초기화한다. 그리고 두 매개변수에 대한 비용함수를 구하고 Gradient Descent를 사용해서 \(x\)와 \(\theta\)를 최적화한다.
이렇게 구한 parameter와 feature를 가지고 \((\theta^{(j)})^T(x^{(i)})\)식을 사용해 점수를 예측한다.
여기서 랜덤값으로 초기화하는 이유는 symmetry breaking을 위해서이다(NN의 파라미터 초기화와 유사). 이러한 초기화는 feature들이 서로 다른 값을 가지도록 보장한다.
- Vectorization : Low Rank Matrix Factorization
이번에는 알고리즘의 벡터화 구현에 대해서 Collbaroative filtering 알고리즘에 적용해보면서 알아보자.

각 유저의 영화 평가 점수는 위와 같이 Y Matrix로 표현이 가능하다.

그리고 Y의 예측값은 오른쪽 Matrix와 같이 \((\theta^{(j)})^T(x^{(i)})\)의 행렬로 표현될 수 있다.
여기서 X Matrix와 \(\Theta\) Matrix를 아래와 같이 정의해보자.
\[X = \begin{bmatrix} -- & (x^{(1)})^T & -- \\ -- & (x^{(2)})^T & -- \\ & \vdots & \\ -- & (x^{(n_m)}) & --\end{bmatrix}\]
\[\Theta = \begin{bmatrix} -- & (\Theta^{(1)})^T & -- \\ -- & (\Theta^{(2)})^T & -- \\ & \vdots & \\ -- & (\Theta^{(n_u)})^T & --\end{bmatrix}\]
이렇게 feature와 parameter들을 각각 Matrix로 만들면, 우리는 \(X\Theta^T\) 행렬 연산을 통해서 예측값을 구할 수 있다. 이러한 방식의 알고리즘을 Low Rank Matrix Factorization 이라고 한다.
Finding related movies
마지막으로, Collaborative Filtering 알고리즘을 사용하면 우리는 관련된 영화를 찾기 위해서 학습된 feature들을 사용할 수 있다. 학습된 feature vector \(x^{(i)}\)는 우리에게 그 영화의 특성을 알려준다. 그렇다면 어떻게 movie i와 유사한 영화들 movies j를 찾을 수 있을까?
직관적으로 우리는 movie i의 feature \(x^{(i)}\)가 movie j의 feature \(x^{(j)}\)가 유사해서, 즉 차이가 작다면, 두 영화는 서로 유사하다고 할 수 있을 것이다. 수식으로 표현하면 아래와 같이 표현할 수 있다.
\[\text{small } \left \| x^{(i)} - x^{(j)} \right \| \rightarrow \text{ movies j and i are "similar"}\]
만약 moive i와 가장 유사한 5개의 영화를 찾는다고 한다면, \(\left \| x^{(i)} - x^{(j)} \right \| \)가 가장 작은 5개의 영화를 찾으면 될 것이다.
- Implementational Detail: Mean normalization
이번에는 알고리즘을 조금 더 잘 동작하게 해줄 수 있는 mean normalization에 대해서 알아보자.

mean normalization에 대해서 알아보기 위해서, 어느 영화에도 평가하지 않은 Eve가 있고 이 데이터를 가지고 Eve에 대해서 Collaborative filtering 알고리즘을 적용해보자.
우선 feature의 개수가 2, 즉, n = 2이라고 가정하고 살펴보도록 하자. \(\theta^{(5)} \in \mathbb{R}^2\)가 되고, \(\theta^{(5)}\)는 Eve의 parameter이다.
어느 영화에도 평가하지 않았기 때문에, Eve의 \(r(i, j)\)모두 0이고, 결국 \(\theta^{(5)}\)는 비용함수의 첫번째항에서 아무런 역할도 하지 못한다. 따라서 \(\theta^{(5)}\)에 영향을 끼치는 것은 두번째항인 정규화항이다. 따라서 우리는 이 정규화항이 작도록 \(\theta^{(5)}\)를 선택해야한다. 다시 말하자면 \(\frac{\lambda}{2}\left [(\theta_1^{(5)})^2 + (\theta_2^{(5)})^2 \right ]\)가 최소가 되어야 한다.
즉, \(\theta^{(5)}\)는 \(\begin{bmatrix} 0 \\ 0 \end{bmatrix}\)가 되어서 \(\theta^{(5)}\)에 대해서 모든 \(x^{(i)}\)를 구하면 모든 값이 0이 될 것이다. \((\theta^{(5)})^T x^{(i)} = 0\).
결국 Eve는 모든 영화에 대해서 0점으로 예측이 된다.
이렇게 구하는 것은 별로 유용하지 않다. 그리고 사용자에서 어느 영화를 추천하기에 좋은 방법도 아니다. 결과적으로 Eve에게 높은 예측값을 갖는 영화는 하나도 없을 것이다.
이러한 문제를 해결하기 위해서 mean normalization을 사용한다.
다음과 같이 영화 점수에 대한 값을 Y matrix로 나타내고, 각 열의 값들의 평균을 구해서 \(u\) vector를 구한다. 그리고 Y matrix에 평균 \(u\) vector를 모든 요소에 대해서 빼서 새로운 Y matrix로 사용한다. 이렇게 하면 각 열의 평균이 0이 된다. 이렇게 변경한 Y matrix를 가지고 parameter \(\theta\)와 \(x\)를 학습한다.
따라서 movie i에 대해서 유저 j가 평가한 예측값은 다음과 같게 된다.

그래서 Eve에 대해서 평가하지 않은 영화에 대해서 예측값을 구하면, 해당 영화의 평균값으로 예측이 된다.
'Coursera 강의 > Machine Learning' 카테고리의 다른 글
| [Machine Learning] Gradient Descent with Large Datasets (0) | 2020.09.05 |
|---|---|
| [Machine Learning] Exam 8 (Week 9) (0) | 2020.09.04 |
| [Machine Learning] Anomaly Detection (0) | 2020.09.02 |
| [Machine Learning] Exam 7 (Week 8) (0) | 2020.08.27 |
| [Machine Learning] Dimensionality Reduction(PCA) (1) | 2020.08.27 |




댓글