Reference
- Algorithms (Sanjoy Dasgupta)
Contents
- The reductions (치환)
이전 포스팅에 이어서 계속 진행해보도록 하겠습니다.
열심히 공부해봤으나... ㅠ 부족한 머리로 아직 완전히 이해를 하진 못해서 설명에 부족한 부분이 많습니다. 이점 유의하시고... 혹시 덧붙이고 싶은 내용이나 정정해야할 부분이 있다면 언제든지 댓글로 남겨주세요 !
The Reductions

이전 포스팅에서 다루었던 문제들이 위의 그림처럼 서로 치환될 수 있음을 살펴볼 예정입니다. 결과적으로 이들은 모두 NP-Complete 입니다. 위 그림에서의 치환들을 살펴보기 전에 먼저 두 가지 버전의 루드라타 문제들을 서로 연관지어 보도록 하겠습니다.
Rudrata (s, t)-Path → Rudrata Cycle
루드라타 순회(rudrata cycle) 문제는 다음과 같습니다.
: 주어진 그래프의 모든 정점을 한 번씩 방문하는 cycle이 존재하는가?
이와 긴밀하게 연관된 루드라타 (s, t)-경로는 그래프의 모든 정점들을 정확히 한 번씩 방문하면서 정점 s에서 출발하여 정점 t로 가는 경로를 찾습니다.
여기서 루드라타 순회 문제가 루드라타 경로 문제보다 쉬울 수 있을까요?
치환(reduction) 방법을 통해 이 질문의 답이 '아니오'라는 것을 밝혀보도록 하겠습니다.
이 치환은 루드라타 경로 문제의 사례(instance) (G = (V, E), s, t)를 루드라타 순회 문제인 G' = (V', E')로 다음과 같이 매핑합니다: G'는 G에 하나의 정점 x, 그리고 이 정점을 끝으로 하는 두 개의 간선 {s, x}와 {x, t}를 추가합니다. 예를 들면 아래의 그림과 같습니다.

따라서, \(V' = V \cup \{x\}\), \(E' = E \cup \{\{s, x\}, \{x, t\}\}\)가 됩니다.
G'에서 루드라타 순회를 찾으면, 이것으로 어떻게 G의 루드라타 경로를 찾을 수 있을까요? 간단히 루드라타 순회에서 간선 {s, x}와 {x, t}만 제거하면 됩니다. 위의 치환 과정을 그림으로 표현하면 다음과 같습니다.

위의 치환이 타당하지 확인하려면, 루드라타 순회가 존재하는 경우와 존재하지 않는 경우 모두에 대해 올바르게 동작함을 보여야 합니다.
1. 루드라타 순회가 존재하는 경우
새로 도입한 정점 x의 이웃은 s와 t뿐이므로 G'의 루드라타 순회는 반드시 간선 {t, x}와 {x, s}를 연속으로 지나가야만 합니다. 순회의 나머지 부분은 s로부터 시작하여 나머지 모든 정점을 통과한 다음 정점 t로 갑니다. 그래서 루드라타 순회에서 두 간선 {t, x}와 {x, s}를 삭제하면 원래 그래프 G에서 정점 s에서 t로 가는 루드라타 경로가 됩니다.
2. 루드라타 순회가 존재하지 않는 경우
이 경우에는 원래 주어졌던 그래프에도 루드라타 경로가 존재하지 않음을 증명해야 합니다. 증명해야 할 명제의 대우, 즉, "G에 루드라타 경로(s, t)가 존재하면, G'에도 루드라타 순회가 존재한다"를 보여야 합니다. 이는 증명하기 쉽습니다. 루드라타 경로에 {t, x}와 {x, s}를 추가하면 루드라타 순회가 됩니다.
마지막으로 매우 중요하지만, 확인하기 쉬운 세부 사항이 있습니다. 이는 전처리와 후처리 함수들이 사례 (G, s, t)의 크기에 대해 다항 시간의 복잡도여야 한다는 것입니다.
다른 방향, 즉 루드라타 순회 문제를 루드라타 경로 문제로 치환하는 것도 가능합니다. 이 치환들로 미루어 두 가지 루드라타 문제는 근본적으로 동일한 문제라는 것을 알 수 있습니다. 두 가지 문제가 매우 비슷하므로 이러한 결론이 별로 놀랄만한 일이 아닐 수 있지만, 아래에서 다루는 치환은 외면상으로 상당히 다르게 보이는 문제들 간의 치환입니다.
3-SAT → Independent Set
3-SAT 문제가 독립집합(Independent Set) 문제로 치환된다고는 생각하기 어려울 수 있습니다. 3-SAT의 입력은 아래와 같이 절(clauses)들의 집합이며, 각 절은 3개 이하의 리터럴(변수)로 구성됩니다.

그리고 문제의 목적은 주어진 부울식이 true가 되도록 각 리터럴에 truth assignment하는 것입니다(진리값 배정).
독립집합 문제의 입력은 그래프와 정수 g이며, 문제의 목적은 서로 이웃하지 않은 g개의 정점을 찾는 것입니다. 따라서 부울 논리를 그래프와 어떻게든 연관시켜야 합니다.
한 번 생각해보겠습니다. 주어진 식을 true로 만들도록 값을 배정하려면, 각 절마다 하나의 리터럴을 선택해 그 값을 true로 배정해야 합니다. 단, 일관성이 있어야 합니다. 즉, 어떤 절에 \(\bar{x}\)를 선택하였다면 다른 어떠한 절에서도 x를 선택해서는 안 됩니다. 각 절에서 하나씩, 일관성 있게 리터럴을 선택하면 이 선택이 바로 truth assignment가 됩니다(이 선택에 포함되지 않는 리터럴에 해당하는 변수는 true든 false든 아무 값이 배정되어도 상관없음).
그래서, 각 절들을 리터럴이 정점인 삼각형으로 나타내보도록 하겠습니다. 예를 들어, (\(x \vee \bar{y} \vee z\))는 정점 \(x, \bar{y}, z\)로 표현됩니다. 삼각형인 이유는 주어진 세 리터럴들을 최대로 연결하는 것이 삼각형이기 때문에 독립집합을 만들 때 이 중에 단 하나의 정점만 선택될 수 있기 때문입니다. 모든 절들을 각각 삼각형으로 표현합니다. 만약 두 개의 리터럴로 구성된 절이 있다면, 하나의 간선으로 이들만 연결하면 됩니다(하나의 리터럴로 구성되는 절이 있다면 그 절은 제외하고 그 리터럴에 true를 배정하면 됨). 결과로 얻는 독립집합은 각 그룹(절)에서 최대 하나의 리터럴만 선택하게 됩니다. 모든 절에서 하나씩을 선택하도록 만들기 위해 목적 g를 절의 개수로 정합니다. 위 식의 경우에는 g = 4가 됩니다.
이제 단 한 가지 빠진 내용은 반대 리터럴(한 절에는 \(x\), 다른 절에서는 \(\bar{x}\))을 선택하는 것을 방지하는 것입니다. 이는 쉬운데, 서로 반대인 리터럴들을 모두 간선으로 연결해놓으면 됩니다. 따라서 처음의 부울식을 이 방식을 통해 아래의 그래프로 표현할 수 있습니다.

위 그래프를 구축하는 방법을 요약하면 다음과 같습니다.
3-SAT 사례(instance) I가 주어지면, 독립집합 문제의 사례 (G, g)를 다음과 같이 생성합니다.
- 각 절마다 절의 리터럴들을 정점으로 하는 삼각형(리터럴이 둘뿐이면 하나의 직선이 됨)을 하나씩 작성하고, 서로 반대인 리터럴을 나타내는 정점들을 모두 간선으로 연결하여 그래프 G를 구축한다.
- 목적 g를 절들의 개수로 결정한다.
위 구축 과정에 소요되는 시간은 명백히 다항 시간입니다. 그러나 치환은 첫 번째 문제를 두 번째 문제로 변형하는 것만으로 끝나는 것이 아니라, 두 번째 문제의 답을 첫 번째 문제의 답으로 재구성하는 방법도 마련해야 합니다.
항상 그러하듯, 여기서 보여야할 것은 두 가지입니다.
1. 그래프 G의 정점의 수가 g인 독립집합 S가 주어질 때, I가 참이 되도록 true assignment하는 방법을 효율적으로 만들 수 있어야 한다.
어떠한 변수 x에 대해, 집합 S는 \(x\)와 \(\bar{x}\)로 레이블된 정점을 모두 포함할 수 없습니다. 왜냐면 그래프를 작성할 때 이러한 정점들을 간선으로 연결해두었기 때문입니다. 그래서 만약 S에 레이블이 x인 정점이 포함되어 있으면 x에 true를 배정하고, S에 레이블이 \(\bar{x}\)인 정점이 포함되어 있으면 x에 false를 배정합니다. 만약 둘 다 포함되어 있지 않으면 x에는 true든 false든 아무거나 배정해도 됩니다. 집합 S에 g개의 정점이 있으므로, 각 절마다 하나씩 정점을 가지고 있는 것이 되며, 위와 같은 truth assignment는 해당 리터럴을 true로 만들기 때문에 결국 모든 절들을 ㅊ마으로 만들게 됩니다.
2. 만약 그래프 G에 크기가 g인 독립집합이 존재하지 않는다면, 부울식 I가 true가 되도록 진리값을 배정하는 것이 불가능하다.
위 명제의 대우인 "I가 참이 되도록 진리값을 배정하는 것이 가능하다면, 그래프 G에 크기 g인 독립집합이 존재한다"를 증명하면 명확합니다. 이 증명은 쉽습니다. I가 true가 되도록 진리값을 배정하는 truth assignment는 각 절마다 적어도 하나의 리터럴에 true를 배정하므로 각 절마다 그 리터럴을 선택하여 해당 정점을 S의 원소로 추가합니다. 그러면 S는 반드시 독립집합이 됩니다.
SAT → 3-SAT
동일한 종류의 특수한 형태로 문제를 치환하는 것은 흥미로우면서도 일반적인 종류의 치환입니다. 이와 같은 치환의 결과, 입력을 특수한 형태로 제한하더라도 문제가 여전히 어렵다는 것을 보일 수가 있는데, 이 경우에는 모든 절의 리터럴의 수를 3개 이하로 제한하더라도 원래의 문제보다 쉬워지지 않음을 보여줍니다. 이러한 치환은 문제의 근본은 그대로 유지하면서 금지된 사항(리터럴이 4개 이상)을 제거하여 주어진 문제를 변형합니다. 원래 문제의 근본을 유지한다는 것은 변형된 문제의 답으로부터 원래 문제의 답을 읽어낼 수 있다는 것입니다.
SAT를 3-SAT로 치환하는 트릭은 다음과 같습니다. SAT의 사례 I가 주어지면, 그대로 3-SAT 문제로 사용하는데, 단, 리터럴의 수가 4개 이상인 절은 다음과 같이 리터럴이 3개인 여러 개의 절들로 대체합니다. (\(a_1 \vee a_2 \vee \cdots \vee a_k\), 여기서 \(a_i\)는 리터럴이고 k > 3인 것들)
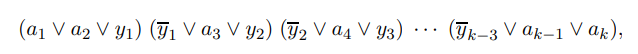
여기서 \(y_i\)는 새로운 변수입니다. 이렇게 얻은 3-SAT의 사례를 I'라고 하겠습니다. I를 I'로 변환하는 과정은 명백히 다항 시간이 걸립니다.
왜 이러한 치환을 하는 걸까요? 이는 satisfiability 관점에서 I'가 I와 동일하기 때문입니다. 왜냐하면 \(a_i\)에 어떠한 값을 배정하든지 아래는 항상 true이기 때문입니다.
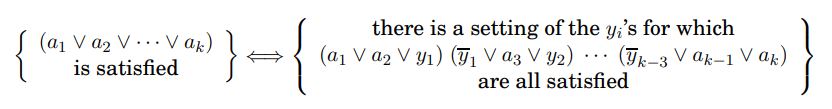
위의 식을 증명하기 위해 우변이 참이라고 가정해봅시다. 즉, 우변의 모든 절들을 true로 하는 \(y_i\)에 대한 truth assignment가 주어졌다고 가정합니다. 그러면 \(a_1, \cdots, a_k\) 중 최소한 하나는 true이어야 합니다. 그렇지 않으면 첫 번째 절을 true로 만들기 위해 \(y_1\)도 true이어야 하는데, \(y_1\)이 true라면 두 번째 절을 true로 만들기 위해 \(y_2\)도 true이어야 하고, 나머지도 이와 같이 되지만 결국 마지막 절이 false가 됩니다. 따라서, "우변의 모든 절들을 true로 하는 \(y_i\)에 대한 truth assignment가 주어졌다면, \(a_1, \cdots, a_k\) 중 최소한 하나는 true이다"라는 명제는 참입니다. 그러나 이는 (\(a_1 \vee a_2 \vee \cdots \vee a_k\)) 또한 만족한다는 것을 의미합니다.
역으로 좌변이 참이면 우변도 참이라는 것을 봅시다. (\(a_1 \vee a_2 \vee \cdots \vee a_k\))가 만족한다는 말은 이 절이 참이 되도록 \(a_1, \cdots, \a_k\)에게 진리값을 부여하는 것이 가능하다는 말이므로, \(a_1 \vee a_2 \vee \cdots \vee a_k\) 중 하나가 true라는 의미입니다. true 값을 배정받은 리터럴을 \(a_i\)라고 가정합시다. 그러면 \(y_1, \cdots, y_{i-2}\)에게는 true를 배정하고 나머지에게는 false를 배정해봅시다. 그러면 우변의 모든 절이 true가 됩니다.
그러므로 SAT의 사례는 무엇이든지 동등한 3-SAT 사례로 변형될 수 있습니다. 나아가서 어떠한 변수도 3개보다 많은 절에 나타날 수 없다는 제약 조건이 추가된 3-SAT도 이러한 제약 조건이 없는 3-SAT와 동일합니다.
(이 명제를 증명하려면 여러 번 나타나는 변수들을 제거해야 합니다)
3-SAT 문제를 제약 조건이 추가된 버전의 3-SAT로 변환하는 방법은 다음과 같습니다. 가령, 주어진 3-SAT 사례에서 변수 x가 k>3인 절에서 나타난다고 가정해봅시다. 그러면 처음 나타나는 x는 \(x_1\), 두 번째 나타나는 x는 \(x_2\)로 바꾸는 방식으로 모든 x를 새로운 변수로 바꾼 다음, 다음과 같은 절들을 원래의 3-SAT 식에 추가합니다.
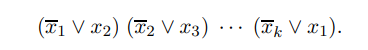
그리고 세 번 이상 나타나는 모든 변수에 대해 반복합니다.
이렇게 변형된 부울식에서는 3번 이상 나타나는 변수는 존재하지 않습니다(사실 두 번 이상 나타나는 리터럴도 없음). 게다가 새로 추가한 식 \((\bar{x}_1 \vee x_2)(\bar{x}_2 \vee x_3)\cdots(\bar{x}_k \vee x_1)\)은 \(x_1, x_2, \cdots, x_k\)가 동일한 값을 갖도록 강제합니다. 따라서 처음 주어진 3-SAT가 true를 가질 수 있는(만족 가능) 필요충분 조건은 위의 제약 조건이 추가된 3-SAT가 만족 가능한 것입니다.
Independent Set → Vertex Cover
어떤 치환은 두 개의 전혀 다른 문제를 연관짓기 위해 교묘한 방법을 쓰지 않으면 안 되는 경우가 있는 반면, 어떤 치환의 경우에는 한 문제가 다른 문제의 위장일 뿐 근본적으로는 동일하다는 사실을 알아차리기만 하면 되는 경우도 있습니다. 독립집합(Independent Set)을 정점 커버(Vertex Cover)로 치환하는 것이 바로 후자에 해당하는 치환입니다. 노드의 집합 S가 그래프 G = (V, E)의 정점 커버일 필요충분 조건은 V-S가 그래프 G의 독립집합인 것입니다.

그래서 독립집합 문제 사례 (G, g)를 풀려면 G의 \(|V|-g\)개의 노드들로 구성된 정점 커버를 찾으면 됩니다. 그러한 정점 커버가 존재하면 거기에 속하지 않은 모든 정점을 독립집합 문제의 답으로 택하면 됩니다. 그러한 정점 커버가 존재하지 않으면 G에는 크기가 g인 독립집합이 존재하지 않습니다.
Independent Set → Clique
독립집합 문제를 클릭 문제로 치환하는 것도 쉽습니다. 그래프 G = (V, E)의 여그래프(complement of a graph)를 \(\bar{G} = (V, \bar{E})\), 단 \(\bar{E}\)는 E에 속하지 않은 정점들의 순서없는 쌍들의 집합이라고 정의합시다. 그러면 노드들의 집합 S가 G의 독립집합일 필요충분 조건은 S가 \(\bar{G}\)의 클릭인 것입니다. 다시 말하면, 그래프 G에서 어떤 정점들의 집합의 원소들간에 간선이 전혀 존재하지 않을 필요충분 조건은 \(\bar{G}\)에서 그 원소들간에 가능한 모든 간선들이 존재하는 것입니다.
그래서 독립집합 문제의 사례 (G, g)를 (\(\bar{G}\), g\)의 클릭 문제로 대응시켜 독립집합 문제를 클릭 문제로 치환할 수 있습니다. 이렇게 치환하면 두 문제의 답은 동일합니다.
3-SAT → 3D Matching
이 문제들은 서로 상이한 문제입니다. 3-SAT 문제를 boy-girl-pet의 삼자묶음(triples)들의 집합 가운데서 boy,girl,pet을 정확히 한 번씩만 포함하는 부분집합을 찾는 문제로 치환해야 합니다. 간단히 말하면, 어떻게 해서든지 부울 변수와 게이트처럼 해동하는 boy-girl-pet 삼자묶음들의 집합을 설계해야 하는 것입니다.
다음 그림에서 보이는 4개의 삼자묶음 집합을 살펴보겠습니다. 각각의 삼자묶음은 boy, girl, pet을 결함하는 삼각형의 노드로 표현됩니다.
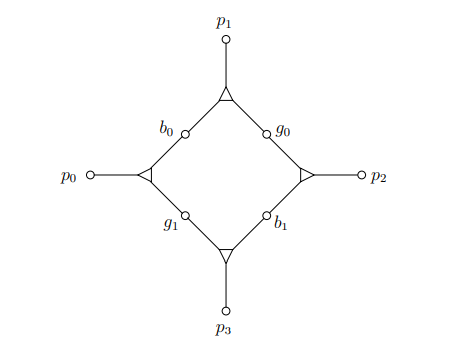
두 명의 소년 \(b_0\)와 \(b_1\) 그리고 두 명의 소녀 \(g_0\)과 \(g_1\)들이 다른 삼자묶음에 속하지 않는다고 가정해봅시다. 그러면 매칭은 (\(b_0, g_1, p_0\))와 (\(b_1, g_0, p_2\))이든지 아니면 (\(b_0, g_0, p_1\))과 (\(b_1, g_1, p_3\))이어야 합니다. 왜냐면 이 두 가지만이 이들 두 소년과 두 소녀가 짝을 지을 수 있는 방법이기 때문입니다. 그러므로 이 장치(gadget, 가젯이라고함)는 가능한 상태가 두 가지밖에 없습니다. 즉, 마치 부울 변수처럼 동작합니다.
그러면 3-SAT 사례를 3D Matching으로 변환하기 위해서, 각각의 변수 x에 대하여 위와 같은 가젯을 하나씩 만듭니다. 그리고 결과로 생성된 노드를 \(p_{x1}, b_{x0}, g_{x1}\) 등으로 명명합니다. 이들이 의미하는 바는 'x = true'이면 소년 \(b_{x0}\)과 소녀 \(g_{x1}\)가 짝이고, 'x = false'라면 소년 \(b_{x0}\)의 짝이 소녀 \(g_{x0}\)이라는 것입니다.
다음은 절을 흉내내는 삼자묶음을 생성해야 합니다. 예를 들어, \(c = (x \vee \bar{y} \vee z)\)와 같은 절들에 대해, 새로운 소년 \(b_c\)와 새로운 소녀 \(g_c\)를 생성합니다. 이들을 절에 있는 리터럴 하나에 하나씩 3개의 삼자묶음에 연관시켜야 합니다.
그리고, 이 삼자묶음에서 pet은 해당 절이 만족될 수 있게 해주는 (1) x= true, (2) y = false, (3) z = true의 세 가지 방법을 반영해야 합니다. (1)의 경우는 (\(b_c, g_c, p_{x1}\))의 삼자묶음을 가질 수 있는데, 여기서 \(p_{x1}\)은 x에 대한 가젯에서의 pet \(p_1\) 입니다. 여기서 \(p_1\)을 선택하는 이유는 x=true라면 \(b_{x0}\)는 \(g_{x1}\)과, 그리고 \(b_{x1}\)은 \(g_{x0}\)과 짝지어지고, 따라서 pet \(p_{x0}\)과 \(p_{x2}\)가 선택되어지기 때문입니다. 이 경우에는 \(b_c\)와 \(g_c\)는 \(p_{x1}\)과 짝지어질 수 있습니다. 그러나 x=false이라면, \(p_{x1}\)과 \(p_{x3}\)이 선택되고, 그래서 \(b_c\)와 \(g_c\)는 이 방법으로는 매칭에 참여시키는 것이 불가능합니다. 동일한 작업을 절의 다른 두 리터럴에 대해서도 수행합니다. 그러면 \(b_c\)와 \(g_c\)를 \(p_{y0}\)나 \(p_{y2}\)와 결합한 삼자묶음(이는 \(\bar{y}\)에 해당하는 것)과 \(p_{z1}\)과 \(p_{z3}\)와 결합한 삼자묶음(이는 z에 해당)이 만들어집니다.
절 c에 나타나는 모든 리터럴 각각에 대해 \(b_c\)와 \(g_c\)에 대응하는 서로 다른 pet이 있도록 해야 합니다. 이는 쉽습니다. 앞서 다룬 치환에서 2번 이상 나타나는 리터럴은 없다고 가정해도 됩니다. 하지만 각 변수 가젯은 false의 경우에 대한 두 개의 pet과 true의 경우에 대한 두 개의 pet을 갖기 때문에 변수 가젯은 충분한 수의 pet을 갖게 됩니다.
이제 치환이 완성된 듯 보입니다. 즉, 매칭으로부터 \(b_{x0}\)가 어느 소녀와 짝지어졌는지 변수 가젯을 하나하나 살펴봄으로써 부울식을 만족하는 truth assignment를 찾을 수 있습니다. 반대로 부울식을 만족하는 truth assignment로부터, x=true이면 (\(b_{x0}, g_{x1}, p_{x0}\))와 (\(b_{x1}, g_{x0}, p_{x2}\))가 선택되고, x=false이면 (\(b_{x0}, g_{x0}, p_{x1}\))와 (\(b_{x1}, g_{x1}, p_{x3}\))이 선택되도록, 그리고 각각의 절 c에 대하여 \(b_c\)와 \(g_c\)를 만족하는 리터럴들 중 하나에 대응하는 pet과 매칭하도록 각각의 변수 x에 대응하는 가젯을 매칭할 수 있습니다.
이제 딱 한 가지 문제가 남았는데, 위에서 정의한 매칭에서 짝이 없는 pet이 발생할 수도 있다는 것입니다. 변수가 n개이고, 절의 수가 m이라면 2n-m마리의 pet이 짝을 찾을 수 없게 되는데, 각 절에는 최소한 두 개의 리터럴이 있고, 변수는 최대 세 번까지 나타나므로 2n-m은 양수일 수 밖에 없습니다. 그러나 이 문제는 2n-m개의 소년-소녀 쌍을 추가하고 모든 pet과 삼자묶음함으로써 쉽게 해결될 수 있습니다.
3D Matching → ZOE
ZOE에서는 0-1 항의 m x n 행렬이 주어지고, m개의 방정식이 만족되도록 0-1 벡터 \(\mathbf{x} = (x_1, \cdots, x_n)\)를 찾아야 합니다. 단, 이 식에서 1은 모든 항이 1인 벡터입니다.
\[\mathbf{Ax} = 1\]
3D Matching을 어떻게 이러한 문제로 표현할 수 있을까요?
ZOE와 ILP는 많은 조합 문제들을 표현할 수 있는 포맷을 제공하기 때문에 매우 유용한 문제입니다. 이러한 포맷에서 0-1 변수는 해를 나타내고, 문제의 제약 조건을 나타내도록 방정식을 작성합니다.
예를 들어, 3D Matching(m명의 소년, m명의 소녀, m명의 애완동물, n개의 trple)의 사례를 ZOE 언어로 표현하는 방법은 다음과 같습니다. n개의 삼자묶음 각각에 대하여 0-1 변수 \(x_i\)(\(x_1, \cdots, x_n\))를 하나씩 사용합니다. 이때 \(x_i = 1\)은 i번째 삼자묶음이 이 매칭에 선택된 것을 나타내고 \(x_i = 0\)은 선택되지 않은 것을 나타냅니다.
이제 남은 것은 \(x_i\)들에 의해 묘사되는 해가 유효한 매칭이라는 말해주는 방정식을 작성하는 것입니다. 소년(or 소녀, 애완동물) 각각에 대하여, 이 소년을 포함하는 삼자묶음을 \(j_1, j_2, \cdots, j_k\)로 번호가 매겨졌다고 가정해봅시다. 그러면 적당한 방정식은 다음과 같습니다.
\[x_{j1} + x_{j2} + \cdots + x_{jk} = 1\]
이 식의 의미는 이들 삼자묶음 중 정확히 하나가 반드시 매칭에 포함되어야 한다는 것입니다. 예를 들어, 아래 그림은 앞서 다룬 적이 있는 3D Matching 문제에 대한 A 행렬입니다.
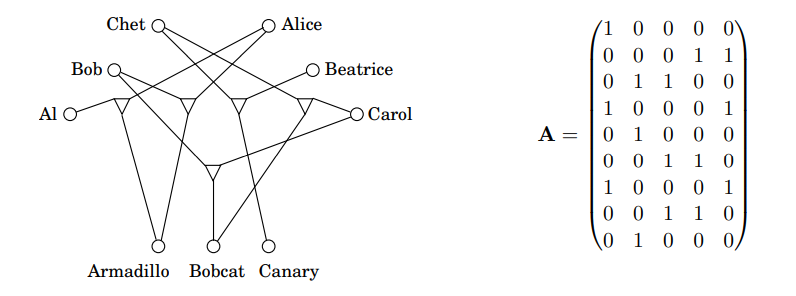
A 행렬의 다섯 개의 열은 가각 5개의 삼자묶음에 대응되며, 9개의 행은 위로부터 차례로 Al, Bob, Chet, Alice, Beatrice, Carol, Armadillo, Bobcat, Canary에 대응합니다.
ZOE → Subset Sum
이 치환은 ILP의 두 가지 특수한 경우에 해당합니다. 하나는 오직 0과 1의 계수를 갖는 방정식을 갖는 경우이고 다른 하나는 계수 제약이 없는 방정식을 갖는 경우입니다. 이 치환은 0-1 벡터는 숫자로 인코딩된다라는 간단하고 익숙한 아이디어게 기반합니다.
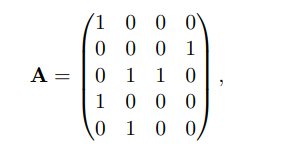
예를 들어, 위와 같은 ZOE 사례가 주어지면, ZOE는 모두 더해질 때 모든 항의 값이 1인 벡터를 만드는 A의 열들의 집합을 찾습니다. 그러나 열들을 위에서부터 아래 순서로 읽는 이진수라고 생각하면 이는 바로 합이 이진수 \(11111_2 = 31\)이 되는 18, 5, 4, 8의 부분집합을 구하는 것과 같습니다. 그리고 이는 부분합(Subset Sum) 문제의 사례이며, 따라서 치환이 완료된 것입니다.
이 방법에서는 0-1 벡터와 이진수간의 밀접한 연관이 있는 carry(올림수)가 이 전략을 망칠 수도 있다는 점을 염두에 두어야 합니다. 예를 들어, 5+6+20=31이며 이를 이진수로 쓰면 \(00101_2 + 00110_2 + 10100_2 = 11111_2\)인데 이와 같이 합이 31인 5비트 이진수들이면서 대응되는 벡터의 합은 (1, 1, 1, 1, 1)이 아닌 경우가 발생합니다. 이런 경우를 고치는 방법은 간단합니다. 열 벡터를 이진수가 아닌 n+1(열의 개수보다 1큼)진수로 생각하면 됩니다. 그러면 최대 n개의 정수들이 합해지므로, 숫자가 모두 9 아니면 1이므로 carry가 발생할 수 없고, 따라서 문제가 해결됩니다.
ZOE → ILP
3-SAT는 SAT의 특수한 케이스이며, 역으로 말하면 SAT는 3-SAT를 일반화한 형태라고 할 수 있습니다. 특수한 케이스라는 것은 3-SAT 사례의 집합은 SAT 사례들의 부분집합이며, 두 문제의 해의 정의는 동일한다는 것을 의미합니다. 결국, 3-SAT에서 SAT로의 치환은 당연히 가능하며, 이러한 치환에서는 입력에 대한 변환도 필요가 없고 해도 그대로 사용하면 됩니다. 즉, 치환을 설명하는 다이어그램에서 함수 f와 h가 모두 입력을 그대로 출력하는 항등함수입니다.
위의 치환이 별게 아니라고 생각들 수 있지만, 주어진 문제가 NP-Complete임을 보이는 데 매우 일반적이며 유용합니다. 즉, 알려진 NP-Complete의 일반화라는 방법으로 NP-Complete임을 보이는 것입니다. 예를 들어, 집합 커버 문제는 정점 커버 문제의 일반화이므로 NP-Complete 입니다.
주어진 문제가 다른 문제의 특수한 케이스임을 보이기 위해 약간의 작업이 필요한 경우가 있습니다. ZOE를 ILP로 치환하는 것이 바로 이러한 경우입니다. ILP에서는 주어진 행렬 A와 벡터 b에 대하여 \(\mathbf{Ax} \leq \mathbf{b}\)를 만족하는 정수 벡터 x를 찾습니다. ZOE의 사례를 이러한 형태로 작성하려면, ZOE의 각 방정식을 두 개의 부등식으로 다시 작성해야 하고, 각 변수 \(x_i\)에 대해 부등식 \(x_i \leq 1\)과 \(-x_i \leq 0\)을 추가해야 합니다.
ZOE → Rudrata Cycle
루드라타 순회 문제는 그래프의 모든 정점을 정확히 한 번씩 지나가는 경로를 찾는 문제입니다. 이 문제가 NP-Complete임을 다음과 같은 두 가지 단계를 거쳐 증명합니다. 먼저 ZOE를 간선의 쌍이 주어진 루드라타 순회(Rudrata Cycle with Paired Edges)라는 문제로 치환합니다. 그 다음 단계에서 이 문제의 추가적인 특징(paired edges)를 제거함으로써 평범한 루드라타 순회 문제로 치환합니다.
간선의 쌍이 주어진 루드라타 순회의 사례에는 그래프 G = (V, E)와 간서의 쌍으로 구성된 집합 \(C \subseteq E \times E\)가 주어집니다. 이 문제에서 할 일은 (1) 루드라타 순회가 그렇듯 모든 정점들을 한 번씩 방문하고 (2) C의 모든 원소인 간선의 쌍 (e, e')에 대하여 e 혹은 e' 중 하나만 경유하는 순회를 찾는 것입니다. 아래 그림의 간단한 예에서는 문제의 해가 굵은 선으로 표시되어 있습니다. 이 그림에서는 둘 이상의 병렬의 간선이 존재한다는 것에 주의합니다. 병렬 간선은 하나의 간선의 복사본이 존재하는 것으로 간주할 수 있는데, 이들이 서로 다른 역할을 할 수 있다는 점에서 대부분의 그래프 문제와는 다릅니다.
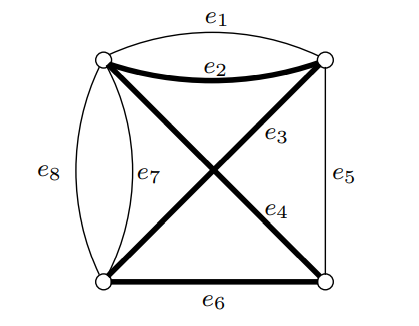
ZOE를 간선 쌍이 주어진 루드라타 순회로 치환하는 방법은 다음과 같습니다.
ZOE의 사례인 \(\mathbf{Ax} = 1\)(A는 n개의 변수로 이루어진 m개의 등식을 나타내는 0-1항의 m x n 행렬)이 주어지면, 아래 그림과 같은 구조를 갖는 그래프를 구축합니다.
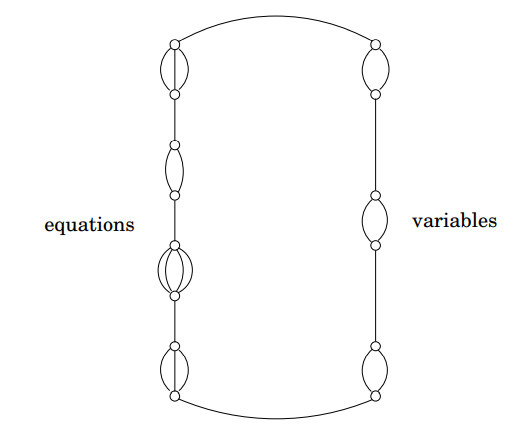
이 그래프의 구조는 병렬 간선들의 모임을 연결하는 순회입니다. 모든 변수 \(x_i\)에 대하여 두 개의 병렬 간선이 그래프에 도입되는데 하나는 \(x_i = 0\)에 해당하는 간선이고, 다른 하나는 \(x_i = 1\)에 해당하는 간선입니다. 그리고 모든 등식 \(x_{j1} + \cdots + x_{jk} = 1\)(k는 변수의 개수)에 대하여 k개의 병렬 간선이 또한 이 그래프에 도입되는데 각 간선은 그 등식에 사용되는 변수를 나타냅니다.
이 그래프의 어떤 루트라타 순회는 반드시 m + n 병렬 간선들의 모임들을 하나하나 차례로 지나가면서 각 모임에서 간선을 하나씩 선택해야 합니다. 이와 같은 방법으로 이 순회는 각 변수에 대하여 0이나 1을 선택하고, 또한 각 등식에 대하여 그 등식에 나타내는 변수를 하나씩 선택합니다.
하지만 치환의 전 과정이 이렇게 간단히 완료되지는 않습니다. 행렬 A의 크기와 구조가 어디에든 반영되어야 하는데, 한 부분이 남아 있는데, 이것이 바로 둘 중 하나만 경유해야 하는 간선 쌍들의 집합인 C입니다. 모든 각각의 등식에 대하여 그리고 그 등식에 나타나는 모든 변수 \(x_i\)에 대하여, (e, e') 쌍을 C에 추가합니다. 단, e는 이 등식에 나타난 \(x_i\)에 해당하는 간선(위 그래프의 왼쪽 부분에 나타나는 간선들)이며, e'는 \(x_i = 0\)을 배정하는 것에 해당하는 간선(위 그래프의 오른쪽 부분)입니다. 그래프의 구성은 이렇게 완성됩니다.
간선 쌍이 주어진 루드라타 순회의 임의의 해를 고려해보도록 하겠습니다. 앞서 논의한 바와 같이 이 해는 각 변수마다 하나의 진리값과 각 등식마다 하나의 변수를 택합니다. 이렇게 선택된 값은 원래 주어진 ZOE의 해가 됩니다. 왜냐면, 변수 \(x_i\)가 1의 값을 가지면 간선 \(x_i = 0\)은 경유되지 않습니다. 그래서 등식 쪽(그래프 쪽 부분)에서 \(x_i\)에 해당하는 간선들은 모두 경유되어야 합니다. 따라서 각 등식마다 그 등식에 나타나는 모든 변수 중 정확히 하나만 1의 값을 갖습니다. 이는 모든 등식이 만족된다고 말하는 것과 같으며, 역방향도 간단합니다. 따라서, ZOE의 해로 루드라타 순회를 쉽게 찾을 수 있습니다.
간선들의 쌍 제거
지금까지 ZOE에서 간선 쌍이 주어진 루드라타 순회 문제로 치환하는 방법을 살펴봤습니다. 우리가 관심있는 것은 일반적인 루드라타 순회 문제에 관심이 있으며, 이는 간선들의 쌍이 있는 문제의 특수한 케이스라고 볼 수 있습니다. 즉, 간선 쌍이 주어진 루드라타 순회 문제에서 C를 공집합으로 두는 경우입니다. 따라서, 간선 쌍이 주어진 루드라타 순회 문제에서 간선 쌍을 제거하는 방법을 찾아야 합니다.
아래의 그래프는 이보다 큰 그래프 G의 일부분이며, 나머지 그래프와 연결된 접점은 정점 a, b, c, d뿐이라고 가정해보겠습니다.
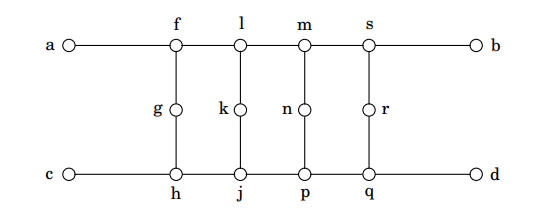
즉, 그래프 G의 루드라타 순회는 위 그래프 부분을 지날 때, 아래 그림의 (b)에 굵은 선으로 표현되는 경로 아니면 (c)에 굵은 선으로 표현되는 경로를 거치게 됩니다.
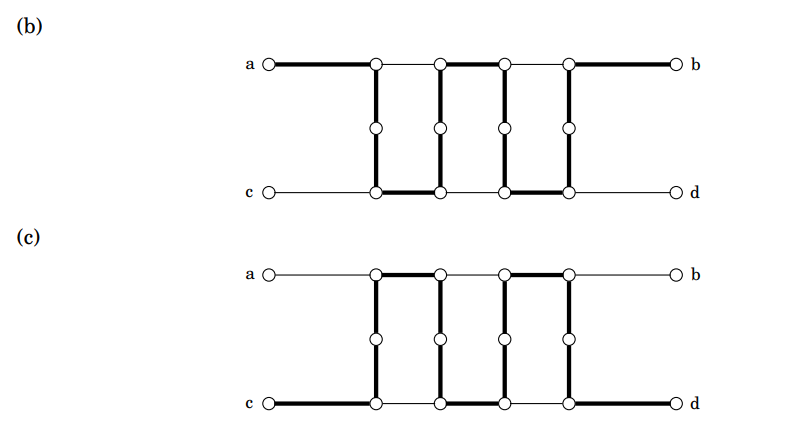
그 이유는 다음과 같습니다.
먼저 루드라타 순회가 정점 a로 들어왔다고 가정해보겠습니다. 그러면 정점 f를 방문해야 하고, 그 다음에는 반드시 정점 g를 방문해야 합니다. 그렇지 않으면 정점 g의 차수가 2이므로 g의 이웃 정점인 f 다음에 g를 방문하지 않으면 순회에 g를 포함하는 것이 불가능하게 됩니다. 그 다음은 h를 방문하게 되는데, 여기에서는 j로 가거나 c로 가는 수 밖에 없다. 그런데 c를 선택하면 루드라타 순회가 그래프의 나머지 부분을 방문하는 것이 불가능하게 됩니다. 따라서 h 다음에는 j를 방문합니다. 그리고 나머지는 위 그림 (b)에서 굵은 선으로 표현한 경로가 됩니다. 이와 동일한 방식으로 루드라타 순회가 정점 c로 들어오면 위 그림 (c)의 굵은 선으로 표현한 경로를 따라 정점 d로 나가는 방법밖에 없습니다.
그러나 이 성질은 매우 중요한 것을 말해줍니다. 위에서 보인 구조(가젯이라고 함)가 간선 쌍이 주어진 루드라타 순회 문제에서 {a, b}와 {c. d}가 쌍을 이룬 것과 동일하다는 것을 말합니다(아래 그림 (d) 참조).

치환의 나머지 과정은 이제 분명합니다. 간선들의 쌍이 주어진 루드라타 순회 문제를 루드라타 순회 문제로 치환하기 위해서 C의 모든 원소인 간선쌍({a, b}, {c, d})을 하나하나 살펴보겠습니다.

각 쌍 ({a, b}, {c, d})를 제거하기 위해 두 개의 간선을 위의 그림의 가젯으로 대체합니다. C에서 간선 {a, b}가 {c, d} 이외에 또 다른 간선과 쌍을 이룬다면, {a, b}를 {a, f}라는 새로운 간선으로 대체합니다. 단, f는 위 그래프에서 보이는 정점입니다. 이제부터 {a, f}를 경유하는 것은 이전 그래프의 간선 {a, b}를 경유하는 것을 나타냅니다. 비슷한 방법으로 {c, h}는 {c, d}를 대체합니다. \(|C|\)번을 대체하고 나면 치환이 완료됩니다. 즉, 이렇게 얻은 그래프의 루드라타 순회는 C의 제약 조건을 만족하는 원래 그래프의 루드라타 순회와 일대일 대응합니다.
Rudrata Cycle → TSP
그래프 G = (V, E)가 주어지면 다음과 같은 TSp 사례를 구성합니다. 도시의 집합은 V와 동일하게 하고, 도시 u와 v의 거리는 {u, v}가 G의 간선이면 1, 아니면 1+\(\alpha\)로 하며, 단, \(\alpha > 1\)인지는 나중에 결정됩니다. TSP의 인스턴스의 예산은 노드의 수 \(|V|\)와 같습니다.
그래프 G에 루드라타 순회가 있다면 그 순회가 TSP 사례의 경비를 만족하는 여행 경로가 되는 것이 자명합니다. 또한, 그래프 G에 루드라타 순회가 없으면 TSP도 해를 찾을 수 없습니다. 왜냐면, 이 경우에는 TSP 여행 경로의 비용이 최소 n+\(\alpha\) 이상이기 때문입니다(길이가 1+\(\alpha\)인 간선을 최소 하나 이상 포함해야 하며, 나머지 n-1개의 길이의 합은 최소 n-1이기 때문). 따라서 루드라타 순회 문제는 TSP 문제로 치환됩니다.
이 치환에서 \(\alpha\)라는 인수를 사용했는데, 이 값을 변화함으로써 두 가지 흥미로운 결과를 얻을 수 있습니다. \(\alpha = 1\)이면 간선의 길이는 모두 1 아니면 2가 됩니다. 그래서 이 경우의 TSP 사례는 삼각부등식을 만듭니다. 즉, i,j,k가 도시라면 \(d_{ij} + d_{jk} \geq d_{ik}\) 입니다(증명: \(1 \leq a, b, c \leq 2\)인 모든 수에 대하여 \(a + b \geq c\) 임). 이것은 TSP의 특수한 케이스로서 실용적으로 중요하며 일반적인 TSP보다 쉽습니다(효율적으로 근사해를 구할 수 있음). 반대로 \(\alpha\)가 크면, TSP 사례가 삼각부등식을 만족하지 않을 수 있습니다. 그 대신 다른 중요한 성질을 하나 갖게 되는데, 그것은 비용이 n이나 그보다 적은 해를 갖든지 아니면 모든 해가 최소 n+\(\alpha\) 이상의 비용을 갖게 되며, 그 사이에는 아무것도 없다는 것입니다.
이 성질은 P = NP가 아닌 한 근사해가 불가능함을 의미합니다.
ANY Problem in NP → SAT
포스팅 처음 그림에서와 같이 SAT를 다양한 문제들로 치환하는 방법을 살펴봤습니다. 이제는 반대로 이러한 모든 문제들 그리고 모든 NP 문제들이 SAT로 치환됨을 살펴보겠습니다.
SAT로 직접 치환하지 않고, 우선 CSAT(Circuit Satisfiability)로 치환합니다. 즉, 모든 NP 문제는 CSAT로 치환됨을 보이고, CSAT는 SAT로 치환됨을 보일 것입니다. CSAT에서는 아래 그림과 같은 부울 회로가 주어집니다.
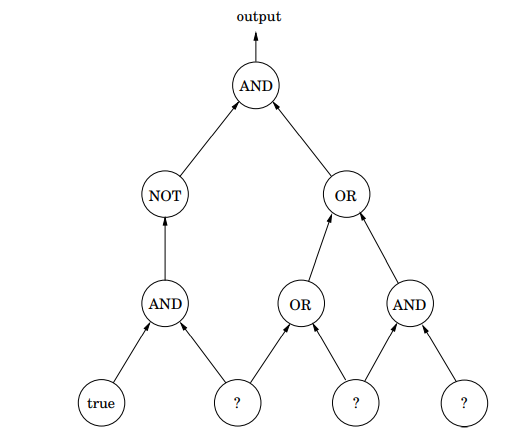
이 부울 회로는 다음과 같은 5가지 유형의 게이트로 구성된 DAG입니다.
- 입력이 두 개인 AND와 OR 게이트(indegree 2)
- 입력이 하나인 NOT 게이트(indegree 1)
- 입력이 없으면 false나 true로 기입된 게이트
- 입력이 없으며 '?'로 기입된 미지의 게이트
이 DAG의 sink 노드는 출력(output) 게이트라고 합니다.
미지의 게이트에 진리값이 주어지면 부울 논리를 적용하여 게이트들을 차례로 계산함으로써 출력 게이트의 값을 구할 수 있습니다. 이 출력 게이트의 값이 주어진 truth assignment에 따른 회로의 값이 됩니다. 예를 들어, 위 그림의 미지의 게이트에 왼쪽에서 차례로 true, false, true일 때, 출력 게이트는 false가 됩니다.
따라서, CSAT는 다음과 같은 탐색 문제(search problem)입니다.
주어진 회로가 true가 되도록 미지의 게이트에 값을 배정하라. 단, 이러한 배정이 불가능하면 불가능하다고 답하라.
위 그림의 회로가 주어지면 CSAT는 (false, true, true)라는 assignment를 찾아줄 것입니다.
CSAT는 SAT의 일반화라고 볼 수 있습니다. 왜냐면 SAT를 구성하는 모든 리터럴들을 미지의 게이트로 나타내고, SAT에서 이들을 연결하는 AND, OR, NOT 연산자들을 AND, OR, NOT 게이트에 연결하면 CSAT로 변환되기 때문입니다.
CSAT를 SAT로 치환하는 것도 가능합니다. 즉, CSAT를 구성하는 모든 게이트에 변수를 대입합니다. 그리고 각 게이트의 효과를 다음의 몇 가지 절들을 사용하여 모델링합니다.
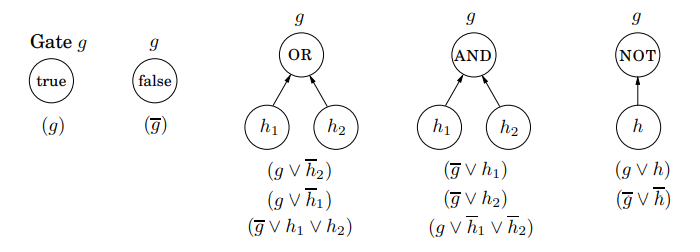
그리고 출력 게이트가 g라면 g로 구성된 절, (g)를 추가합니다. 이렇게 얻은 SAT는 CSAT와 동일합니다. 즉, 이렇게 얻은 부울식을 true로 하는 truth assignment는 원래 주어진 회로를 true로 하며 역도 성립합니다.
CSAT가 SAT로 치환되므로 모든 탐색 문제가 CSAT로 치환됨을 보이면 됩니다.
A가 NP 문제라고 합시다. A를 CSAT로 치환하는 방법을 찾아야 하는데, A에 대하여 아는 바가 없으므로 이 작업은 매우 어려울 듯 합니다.
A에 대해 우리가 알고 있는 것은 A가 탐색 문제라는 것 뿐이므로, 이를 이용해야 합니다. 탐색 문제의 주요한 특징은 해당 문제에 대한 모든 솔루션을 빠르게 확인할 수 있다는 것입니다. 검증 알고리즘 C는 문제의 사례 I와 솔루션 S가 주어지면 S가 I의 해인지 아닌지를 판정합니다. 나아가서, C는 \(|I|\)에 대한 다항식 시간 내에 이러한 판정을 내립니다. 또한 S는 이진 문자열로 표현될 수 있으며 S의 길이도 \(|I|\)에 대한 다항식이라고 할 수 있습니다.
모든 알고리즘은 결국 컴퓨터로 실행됩니다. 그리고 컴퓨터는 칩에 구현된 부울 조합 회로입니다. 어떤 알고리즘이 다항 시간 내에 실행된다면 알고리즘이 컴퓨터에 실행되는 과정은 CSAT 회로로 표현하는 것이 가능합니다. 즉, 이 CSAT는 다항식 시간에 해당하는 다항식 계층으로 구성되며, 각 층은 컴퓨터 회로의 상태를 나타내는데 다항식 시간 복잡도의 알고리즘이 참조하는 장소의 수가 다항식보다 클 수 없으므로 각 층도 다항식 수의 게이트로 구성됩니다. 따라서, 모든 다항식 시간 복잡도의 알고리즘은 다항식 게이트 수의 CSAT로 치환이 가능합니다.
모든 다항식 알고리즘은회로로 표현이 가능하고, 이때 입력 게이트는 알고리즘의 입력에 해당합니다. 따라서 입력 비트가 많으면 회로도 그에 따라 커지겠지만, 아무튼 총 게이트의 수는 입력에 대한 다항식입니다. 그런데 다항식 알고리즘이 'yes' 또는 'no'로 답한다면 이 답이 바로 회로의 출력값이 됩니다.
그래서 문제 A의 사례 I와 솔루션 S가 주어지면 사례 I를 알려진 게이트로, 솔루션 S를 미지의 게이트로 표현하고 S가 I의 해일 때 'yes'를 출력하고 아니면 'no'를 출력하는 회로를 다항식 시간 내에 구축할 수 있습니다. 즉, 이 회로가 true를 출력하도록 미지 게이트에 값을 배정하는 것이 문제 A의 사례인 I의 해와 일대일 대응합니다. The reduction is complete.
저는 여기서 설명하는 문제들을 푸는 방법도 완벽히 이해하지 못하고 있고, 책에서 설명하는 내용도 어려워서 아직 완벽하게 이해하지 못한 것 같습니다... ㅠ
기회가 된다면 조금 더 자세히 설명해주는 책을 살펴봐야 할 것 같습니다...
'Data Structure & Algorithm > 알고리즘' 카테고리의 다른 글
| 2-SAT (1) | 2022.04.28 |
|---|---|
| NP-Complete Problems (1) (0) | 2022.04.23 |
| 강한 연결 요소 (Strongly Connected Component) (0) | 2022.04.22 |
| 이분 매칭 (Bipartite Matching) (0) | 2022.04.21 |
| 포드 풀커슨 / 에드몬드 카프 알고리즘 (0) | 2022.04.20 |




댓글