References
- Algorithm (Sanjoy Dasgupta)
Contents
- SCC (Strongly Connected Component)
- 백준 2150 : Strongly Connected Component
- 코사라주 알고리즘 (Kosaraju Algorithm)
Connectivity for directed graphs
무향 그래프(undirected graph)에서 연결성(connectivity)는 꽤 명확합니다. 연결이 안된 그래프는 자연스럽게 여러 연결된 요소들로 분리될 수 있습니다.
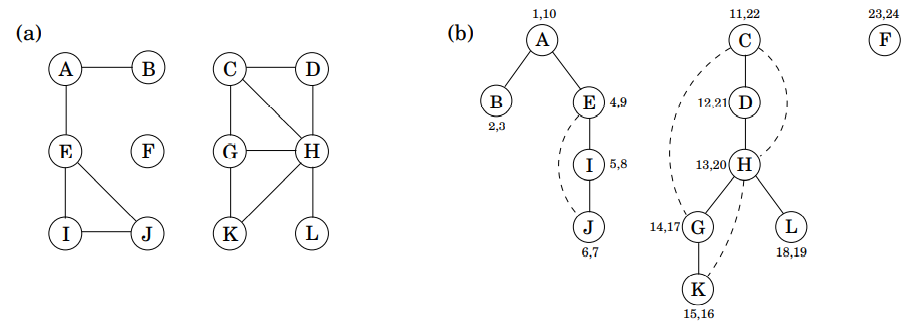
무향 그래프는 만일 정점들의 임의의 쌍 사이에 경로가 있다면 연결되었다고 할 수 있습니다. 위 이미지에서 (a) 그래프는 전부 연결되지는 않았습니다. 따라서 아래의 세 집합에 대응되는 3가지의 다른 연결된 성분을 지니고 있습니다.
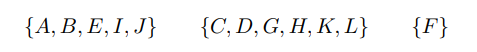
그리고 DFS를 통해서 각 연결된 요소(connected component)는 속하는 집합의 번호를 할당하여 각 집합을 아주 쉽게 구분할 수 있습니다.
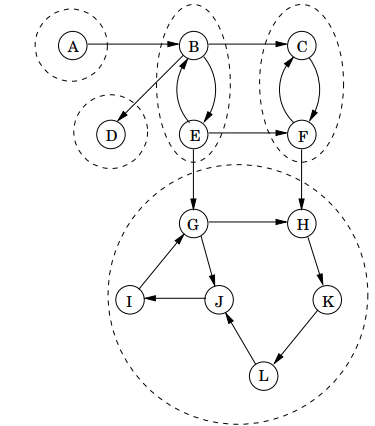
하지만, 유향 그래프에서 연결성은 조금 더 복잡합니다. 본능적인 직감으로 아래 이미지의 유향 그래프는 'connected'된 것입니다(모든 정점들의 쌍이 간선으로 연결되어 있으므로).

하지만 이러한 개념은 별로 도움이 되지 않습니다. 따라서 유향 그래프를 위해 연결성(connectivity)를 정의하는 올바른 방법은 다음과 같습니다.

이러한 관계는 강한 연결 요소(SCC; strongly connected components)라고 부르는 서로 다른 집합으로 분할합니다. 예를 들어, 위 그래프에서 G에서 B로, 또는 F로부터 A로의 경로가 없기 때문에 무향 그래프의 연결성 개념으로는 모두 연결되었다고 볼 수 있지만, 유향 그래프에서의 연결성 개념에서는 연결된 것으로 여기지 않습니다.
이제 각각의 강하게 연결된 요소를 하나의 메타-노드(meta-node)로 줄여보겠습니다. 그리고 각각의 성분들 사이에 간선이 있다면 아래와 같이 간선을 그립니다.

결과적으로 이 그래프는 DAG임이 틀림없습니다. 왜냐면, 여러 강한 연결 요소를 포함하는 사이클은 이들을 하나의 강한 연결 요소로 병합하기 때문입니다. 즉 아래의 특성을 만족합니다.
Property: 모든 유향 그래프는 자신의 강한 연결 요소들의 DAG이다.
이는 다음의 중요한 사실을 말합니다: 유향 그래프의 연결성 구조는 두 개의 계층으로 되어 있습니다. 예를 들어, Top-level에는 선형화될 수 있는 다소 간단한 구조인 DAG가 있습니다. 더 자세한 정보를 원하면 이 DAG의 노드 중 하나를 살펴보고 그 안에 있는 강한 연결 요소를 검사할 수 있습니다.
An efficient algorithm
유향 그래프를 강한 연결 요소로 분할하는 것은 매우 유익하고 유용합니다. 다행히 DFS를 사용하여 선형 시간 안에 분할할 수 있다는 것이 증명되었습니다. 이 알고리즘은 아래에서 보여줄 속성들에 기반을 두고 있습니다.
속성들을 살펴보기 전에 여기서 설명할 DFS의 의사 코드는 다음과 같습니다.

그리고 explore 함수의 의사 코드는 다음과 같습니다.

위 의사 코드에서 previsit과 postvisit은 노드의 방문 순서를 나타내며 previsit은 DFS에서 해당 노드에 처음 들어왔을 때의 순서, postvisit은 해당 노드에서 DFS가 끝나고 해당 explore 함수를 벗어날 때 기록되는 순서입니다.
다시 SCC에 대해서 살펴보도록 하겠습니다.
Property 1: 만약 explore 서브루틴이 노드 u에서 시작되면 u에서 도달할 수 있는 모든 노드를 방문했을 때 종료된다.
위 속성으로 인해, 만약 강한 연결 요소 sink(메타 그래프에서 강한 연결 요소인)의 어딘가에 놓인 노드에서 explore를 호출한다면, 정확히 그 요소를 가져올 것입니다. 아래 그림에서는 {D}와 {G,H,I,J,K,L}, 2개의 싱크가 존재합니다.

예를 들면, 만약 노드 K에서 explore를 시작하고, K에서 도달할 수 있는 노드들을 모두 순회하고 멈춥니다.
이는 하나의 강한 연결 요소를 찾는 한 가지 방법을 제안합니다. 하지만, 여전히 다음의 2가지 중요한 문제는 남아있습니다.
- 강한 연결 요소 sink 내에 분명히 놓이는 노드는 어떻게 찾을 것인가?
- 첫 번째 요소를 발견한 다음 어떻게 계속 진행할 것인가?
첫 번째 문제부터 살펴보겠습니다. 강한 연결 성분 sink에 놓여진다고 보장되는 노드를 고르는 쉽고 직관적인 방법은 없습니다. 하지만 강한 연결 성분 source에서 노드를 얻은 방법은 있습니다.
Property 2: DFS에서 가장 높은 post 숫자를 받는 노드는 강한 연결 성분 source에 놓여 있어야 한다.
이는 아래의 더 일반화된 속성으로부터 따라옵니다.
Property 3: 만약 C와 C'가 강한 연결 요소이고, C 안에 있는 노드로부터 C' 안에 있는 노드로의 간선이 있다면, C 안에서 가장 높은 post 숫자는 C' 안에 있는 가장 높은 post 숫자보다 더 크다.
속성 3은 강한 연결 요소들을 post 숫자들의 내림차순으로 배치함으로써 선형화될 수 있다는 것을 말합니다. 이는 DAG를 선형화하는 알고리즘의 일반화입니다. 그리고 DAG에서 각 노드는 그 자체로 강한 연결 성분입니다.
속성 2는 G의 강한 연결 성분 source에서 노드를 찾는 데 도움을 줍니다. 그렇지만, 필요한 것은 sink 요소에 있는 노드입니다. 따라서 우리가 필요한 것과는 정반대인 것처럼 보입니다. 그러나 G와 동일하지만 모든 간선이 반전된 역그래프 \(G^R\)을 고려해보겠습니다(아래 이미지 참조).

\(G^R\)은 정확히 G와 같은 강한 연결 요소를 가지고 있습니다. 따라서 \(G^R\)에서 DFS를 하면, 가장 높은 post 숫자를 지닌 노드는 \(G^R\)에서 강한 연결 요소 source이며, 즉, G에서의 강한 연결 요소 sink 입니다.
이 방식으로 첫 번째 문제를 해결할 수 있습니다.
이제 두 번째 문제를 살펴보겠습니다.
첫 번째 sink 요소가 확인된 다음에는 어떻게 해야 할까요?
그 해답 또한 속성 3에 의해 제공됩니다. 일단 첫 번째로 강한 연결 요소를 찾으면 그래프로부터 이들은 삭제하고, 남은 노드들 중에 가장 높은 post 숫자를 지닌 노드는 G에 무엇이 남았는지에 상관없이 강한 연결 요소 sink에 속하게 됩니다. 따라서 \(G^R\)에 대한 초기 DFS에서의 post 숫자를 계속 사용하여 두 번째 강한 연결 요소, 세 번째 강한 연결 요소 등을 연속적으로 찾을 수 있습니다.
결과적으로 알고리즘은 다음과 같습니다.
- \(G^R\)에 대해 DFS 탐색을 수행한다.
- \(G\)에 대한 무향 강한 연결 요소 알고리즘을 수행하고, DFS를 수행하는 동안 1번으로부터 얻은 post 번호의 내림차순으로 정점을 처리한다.
이 알고리즘은 선형 시간이며, 선형 항의 유일한 상수는 straight DFS의 두 배입니다.
그럼 다시 그래프 G를 가져와서, 이 그래프에 대해 위 알고리즘을 실행시켜봅시다.
1. 먼저 그래프 G에 대한 역그래프 \(G^R\)을 구합니다. 위 그래프 G의 역그래프는 아래와 같습니다.

2. 역그래프 \(G^R\)에 대해 DFS를 수행합니다. 이때, 실행할 노드 순서는 그냥 사전순으로 진행하고, DFS를 돌면서 각 노드의 post number를 할당해줍니다. 이렇게 할당된 post number는 다음과 같습니다.

이렇게 역그래프로부터 추출한 post 값들에서 가장 큰 노드는 역그래프의 강한 연결 요소에서 source가 됩니다. 따라서 이 노드는 원 그래프의 강한 연결 요소의 sink입니다. post 숫자가 큰 순서대로 나열하면 다음과 같습니다.
[G I J L K H D C F B E A]
3. 이제 원 그래프 G에 대해 DFS를 수행합니다. 이때, 실행할 노드 순서는 POST 숫자가 가장 큰 노드부터 내림차순으로 수행합니다. 어느 한 노드에서 DFS를 수행하며 방문한 모든 노드는 하나의 강한 연결 요소를 구성합니다. 따라서 이 과정을 거치고 나면, {G, H, I, J, K, L}, {D}, {C, F}, {B, E}, {A}와 같은 순서로 강한 연결 요소들을 추출하게 됩니다.

위 이미즈의 결과는 알고리즘을 구현한 아래의 코드를 실행한 결과입니다. 위의 알고리즘을 거의 그대로 구현하였으므로, 코드를 살펴보시면 금방 이해하실 것이라고 생각됩니다. 여기서 post 숫자가 가장 큰 노드를 추출하기 위해 간단히 우선순위 큐를 사용하였습니다.
#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>
#include <functional>
void set_graph(std::vector<std::vector<int>>& graph, int u, int v)
{
graph[u].push_back(v);
}
std::vector<std::vector<int>> get_reversed_graph(std::vector<std::vector<int>>& graph)
{
const int V = graph.size();
std::vector<std::vector<int>> reversed_graph(V);
for (int u = 0; u < V; u++) {
for (auto v : graph[u]) {
reversed_graph[v].push_back(u);
}
}
return reversed_graph;
}
void post_visit(std::vector<int>& post, const int v)
{
static int clock = 0;
post[v] = clock++;
}
// dfs to get post number
void dfs(const int cur, std::vector<bool>& visited, std::vector<int>& post, const std::vector<std::vector<int>>& graph)
{
visited[cur] = true;
for (auto next : graph[cur]) {
if (!visited[next]) {
dfs(next, visited, post, graph);
}
}
post_visit(post, cur);
}
// dfs to get SCC
void dfs(const int cur, std::vector<int>& scc, std::vector<bool>& visited, const std::vector<std::vector<int>>& graph)
{
visited[cur] = true;
scc.push_back(cur);
for (auto next : graph[cur]) {
if (!visited[next]) {
dfs(next, scc, visited, graph);
}
}
}
int main(int argc, char* argv[])
{
int V = 12;
std::vector<std::vector<int>> graph(V);
// set graph
graph[0].push_back(1); // A->B
graph[1].push_back(2); // B->C
graph[1].push_back(3); // B->D
graph[1].push_back(4); // B->E
graph[2].push_back(5); // C->F
graph[4].push_back(1); // E->B
graph[4].push_back(5); // E->F
graph[4].push_back(6); // E->G
graph[5].push_back(2); // F->C
graph[5].push_back(7); // F->H
graph[6].push_back(7); // G->H
graph[6].push_back(9); // G->J
graph[7].push_back(10); // H->K
graph[8].push_back(6); // I->G
graph[9].push_back(8); // J->I
graph[10].push_back(11); // K->L
graph[11].push_back(9); // L->J
// get reversed graph
auto reversed_graph = get_reversed_graph(graph);
// set init variables
std::vector<bool> visited(V, false);
std::vector<int> post(V, -1);
// 1. run dfs on reversed_graph
for (int u = 0; u < V; u++) {
if (!visited[u]) {
dfs(u, visited, post, reversed_graph);
}
}
// set priority queue
std::priority_queue<std::pair<int, int>> pq;
for (int u = 0; u < V; u++) {
pq.push({ post[u], u });
}
std::fill(visited.begin(), visited.end(), false);
// 2. run dfs on graph
std::vector<std::vector<int>> SCC;
while (!pq.empty()) {
int cur = pq.top().second;
pq.pop();
std::vector<int> curSCC;
if (!visited[cur]) {
dfs(cur, curSCC, visited, graph);
sort(curSCC.begin(), curSCC.end());
SCC.push_back(curSCC);
}
}
// print SCC
printf("%d\n", SCC.size());
sort(SCC.begin(), SCC.end());
for (auto& curSCC : SCC) {
for (int cur : curSCC) {
printf("%d ", cur + 1);
}
printf("-1\n");
}
}
백준 2150 : Strongly Connected Component
https://www.acmicpc.net/problem/2150
2150번: Strongly Connected Component
첫째 줄에 두 정수 V(1 ≤ V ≤ 10,000), E(1 ≤ E ≤ 100,000)가 주어진다. 이는 그래프가 V개의 정점과 E개의 간선으로 이루어져 있다는 의미이다. 다음 E개의 줄에는 간선에 대한 정보를 나타내는 두 정
www.acmicpc.net
백준의 위 알고리즘을 테스트할 만한 문제가 있습니다. 단순히 입력을 받는 부분과 출력만 수정해주고, 알고리즘 코드는 위의 것을 그대로 사용했습니다.
#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>
#include <functional>
void set_graph(std::vector<std::vector<int>>& graph, int u, int v)
{
graph[u].push_back(v);
}
std::vector<std::vector<int>> get_reversed_graph(std::vector<std::vector<int>>& graph)
{
const int V = graph.size();
std::vector<std::vector<int>> reversed_graph(V);
for (int u = 0; u < V; u++) {
for (auto v : graph[u]) {
reversed_graph[v].push_back(u);
}
}
return reversed_graph;
}
void post_visit(std::vector<int>& post, const int v)
{
static int clock = 0;
post[v] = clock++;
}
// dfs to get post number
void dfs(const int cur, std::vector<bool>& visited, std::vector<int>& post, const std::vector<std::vector<int>>& graph)
{
visited[cur] = true;
for (auto next : graph[cur]) {
if (!visited[next]) {
dfs(next, visited, post, graph);
}
}
post_visit(post, cur);
}
// dfs to get SCC
void dfs(const int cur, std::vector<int>& scc, std::vector<bool>& visited, const std::vector<std::vector<int>>& graph)
{
visited[cur] = true;
scc.push_back(cur);
for (auto next : graph[cur]) {
if (!visited[next]) {
dfs(next, scc, visited, graph);
}
}
}
int main(int argc, char* argv[])
{
int V, E;
scanf("%d %d", &V, &E);
std::vector<std::vector<int>> graph(V);
int u{}, v{};
for (int i = 0; i < E; i++) {
scanf("%d %d", &u, &v);
set_graph(graph, u - 1, v - 1);
}
// get reversed graph
auto reversed_graph = get_reversed_graph(graph);
// set init variables
std::vector<bool> visited(V, false);
std::vector<int> post(V, -1);
// 1. run dfs on reversed_graph
for (int u = 0; u < V; u++) {
if (!visited[u]) {
dfs(u, visited, post, reversed_graph);
}
}
// set priority queue
std::priority_queue<std::pair<int, int>> pq;
for (int u = 0; u < V; u++) {
pq.push({ post[u], u });
}
std::fill(visited.begin(), visited.end(), false);
// 2. run dfs on graph
std::vector<std::vector<int>> SCC;
while (!pq.empty()) {
int cur = pq.top().second;
pq.pop();
std::vector<int> curSCC;
if (!visited[cur]) {
dfs(cur, curSCC, visited, graph);
sort(curSCC.begin(), curSCC.end());
SCC.push_back(curSCC);
}
}
// print SCC
printf("%d\n", SCC.size());
sort(SCC.begin(), SCC.end());
for (auto& curSCC : SCC) {
for (int cur : curSCC) {
printf("%d ", cur + 1);
}
printf("-1\n");
}
}
코사라주 알고리즘
참고로 위 알고리즘은 코사라주 알고리즘(Kosaraju Algorithm)과 유사합니다. 단지 차이점은 위 알고리즘은 역그래프에 DFS를 수행하면서 post number를 부여하는 것이고, 코사라주 알고리즘은 마찬가지로 역그래프에 DFS를 수행하지만, post number를 부여하는 위치에서 해당 정점을 스택에 push하는 것입니다. 그리고 2번째 스텝에서 스택에서 정점들을 pop하고 DFS를 돌며 SCC를 찾는 것입니다. 당연히 스택에는 post number가 작은 것이 먼저 push되고 큰 것이 나중에 push됩니다. 따라서 위 알고리즘과 동일한 순서로 2번째 스텝을 진행하게 됩니다.
다른 SCC 추출 알고리즘으로 타잔 알고리즘(Tarjan's Algorithm)이 있습니다. 자세히는 못봤지만, 책에서 설명하는 알고리즘이 조금 더 기억하기도 쉽고 구현도 쉬운 것 같아서, 타잔 알고리즘은 따로 다루지 않았습니다. 타잔 알고리즘은 아래 블로그에서 자세히 설명해주고 있으니, 관심있으시면 참고바랍니다.. !
https://blog.naver.com/kks227/220802519976
구현 코드는 다음과 같습니다. 첫 번째 단계에서 DFS를 수행할 때, 이번에는 post number가 아닌 stack에 방문한 정점을 post 위치에서 push하도록 변경하였습니다. 그리고 우선순위 큐를 사용할 필요없이 stack에서 pop하면서 정점들을 처리하게 됩니다. 아래 코드도 마찬가지로 백준 2150번 문제를 pass 합니다.
#include <iostream>
#include <vector>
#include <stack>
#include <algorithm>
void set_graph(std::vector<std::vector<int>>& graph, int u, int v)
{
graph[u].push_back(v);
}
std::vector<std::vector<int>> get_reversed_graph(std::vector<std::vector<int>>& graph)
{
const int V = graph.size();
std::vector<std::vector<int>> reversed_graph(V);
for (int u = 0; u < V; u++) {
for (auto v : graph[u]) {
reversed_graph[v].push_back(u);
}
}
return reversed_graph;
}
void post_visit(std::vector<int>& post, const int v)
{
static int clock = 0;
post[v] = clock++;
}
// dfs to get post number
void dfs(const int cur, std::vector<bool>& visited, std::stack<int>& st, const std::vector<std::vector<int>>& graph)
{
visited[cur] = true;
for (auto next : graph[cur]) {
if (!visited[next]) {
dfs(next, visited, st, graph);
}
}
st.push(cur);
}
// dfs to get SCC
void dfs(const int cur, std::vector<int>& scc, std::vector<bool>& visited, const std::vector<std::vector<int>>& graph)
{
visited[cur] = true;
scc.push_back(cur);
for (auto next : graph[cur]) {
if (!visited[next]) {
dfs(next, scc, visited, graph);
}
}
}
int main(int argc, char* argv[])
{
int V, E;
scanf("%d %d", &V, &E);
std::vector<std::vector<int>> graph(V);
int u{}, v{};
for (int i = 0; i < E; i++) {
scanf("%d %d", &u, &v);
set_graph(graph, u - 1, v - 1);
}
// get reversed graph
auto reversed_graph = get_reversed_graph(graph);
// set init variables
std::vector<bool> visited(V, false);
std::stack<int> st;
// 1. run dfs on reversed_graph
for (int u = 0; u < V; u++) {
if (!visited[u]) {
dfs(u, visited, st, reversed_graph);
}
}
std::fill(visited.begin(), visited.end(), false);
// 2. run dfs on graph
std::vector<std::vector<int>> SCC;
while (!st.empty()) {
int cur = st.top();
st.pop();
std::vector<int> curSCC;
if (!visited[cur]) {
dfs(cur, curSCC, visited, graph);
sort(curSCC.begin(), curSCC.end());
SCC.push_back(curSCC);
}
}
// print SCC
printf("%d\n", SCC.size());
sort(SCC.begin(), SCC.end());
for (auto& curSCC : SCC) {
for (int cur : curSCC) {
printf("%d ", cur + 1);
}
printf("-1\n");
}
}
'Data Structure & Algorithm > 알고리즘' 카테고리의 다른 글
| NP-Complete Problems (2) (0) | 2022.04.25 |
|---|---|
| NP-Complete Problems (1) (0) | 2022.04.23 |
| 이분 매칭 (Bipartite Matching) (0) | 2022.04.21 |
| 포드 풀커슨 / 에드몬드 카프 알고리즘 (0) | 2022.04.20 |
| 선형 계획법과 치환 (3) - 쌍대성, 심플렉스법 (0) | 2022.04.19 |




댓글