Contents
- 이분 매칭 (Bipartite Matching)
- 백준 2188 : 축사 배정
선형 계획법과 치환 (2) - Network Flow, Bipartite Matching
위 포스팅에서 네트워크 유량과 이분 매칭에 대해서 알아봤었는데, 이번 포스팅에서는 이분 매칭을 어떻게 구현하느냐에 초첨을 맞추어 보려고 합니다.
지난 포스팅에서 이분 매칭은 최대 유량(maximum flow) 문제로 치환되어 선형 계획법을 사용할 수 있다고 했었는데, 즉, 최대 유량 문제를 풀듯이 풀 수 있다는 것 입니다.
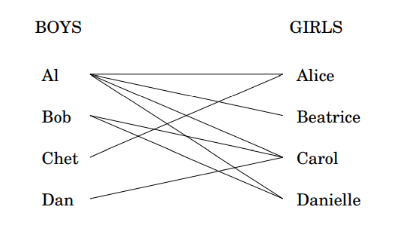
위에서 소년들과 소녀들을 매칭하는 문제에서,
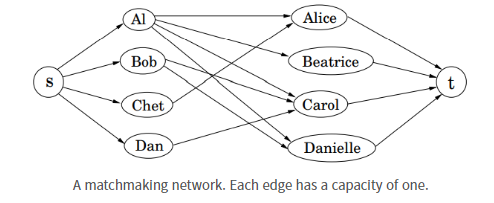
위의 그래프처럼 모든 소년들을 향해 나가는 간선들을 갖는 새로운 source 노드와 모든 소녀들로부터 들어가는 간선들을 갖는 새로운 sink 노드 t를 만들고, 모든 간선의 용량을 1로 설정합니다. 이때 그래프에서 최대로 매칭시킬 수 있는 커플들을 찾는 문제를 최대 매칭(maximum matching) 문제라고 하며, 만약 네트워크에서 생성되는 최대 커플 수와 같다면 퍼펙트 매칭(perfect mathcing)이라고 합니다.
백준 2188 : 축사 배정
https://www.acmicpc.net/problem/2188
2188번: 축사 배정
농부 존은 소 축사를 완성하였다. 축사 환경을 쾌적하게 유지하기 위해서, 존은 축사를 M개의 칸으로 구분하고, 한 칸에는 최대 한 마리의 소만 들어가게 계획했다. 첫 주에는 소를 임의 배정해
www.acmicpc.net
위의 문제가 이분 매칭으로 분류되는 문제입니다.
앞서 언급했듯이 이분 매칭은 네트워크 유량, 즉, 최대 유량 풀이로 해결할 수 있습니다.
따라서, 아래 포스팅에서 다루었던 에드몬드 카프 알고리즘을 사용하여 위 문제를 해결해보도록 하겠습니다.
다만, 위 포스팅에서 사용했던 구현을 약간 수정해주어야 하는데, 사실 입력을 받는 부분과 이분 그래프 왼쪽에 source를 추가해주는 작업과 오른쪽에 sink를 추가해주는 작업을 추가한 것을 제외한 나머지 코드는 동일합니다.
#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>
const int INF = 123456789;
void set_graph(std::vector<std::vector<int>>& graph, const int u, const int v, const int c)
{
graph[u][v] = c;
//graph[v][u] = -c;
}
bool bfs(const int s, const int t, const int n, const std::vector<std::vector<int>>& graph, std::vector<int>& prev, std::vector<bool>& visited)
{
// init value
for (int i = 0; i < n; i++)
visited[i] = false;
// create a queue for BFS
std::queue<int> q;
// mark s node as visited and enqueue it
q.push(s);
visited[s] = true;
int u{};
while (!q.empty()) {
u = q.front();
q.pop();
// get adjacent vertices
for (int v = 0; v < n; v++) {
if (visited[v] == false && graph[u][v] > 0) {
q.push(v);
visited[v] = true;
prev[v] = u;
}
}
}
return visited[t];
}
int edmonds_karp(const int source, const int sink, const int n, std::vector<std::vector<int>>& graph)
{
std::vector<bool> visited;
std::vector<int> prev;
// init value
visited.resize(n, false);
prev.resize(n, -1);
int max_flow{ 0 };
int path_flow{}, s{}, u{}, v{};
while (bfs(source, sink, n, graph, prev, visited)) {
path_flow = INF;
// find minimum capacity of the edges along the path by BFS
s = sink;
while (s != source) {
path_flow = std::min(path_flow, graph[prev[s]][s]);
s = prev[s];
}
// add path flow to overall flow
max_flow += path_flow;
// update residual copacities of the edges and reverse edges along the path
v = sink;
while (v != source) {
u = prev[v];
graph[u][v] -= path_flow;
graph[v][u] += path_flow;
v = prev[v];
}
}
return max_flow;
}
int main(int argc, char* argv[])
{
std::vector<std::vector<int>> graph;
// set graph
int n{}, m{};
scanf("%d %d", &n, &m);
int total{}, e{};
total = n + m;
graph.resize(total +2, std::vector<int>(total +2, 0));
// add edges outgoing from source(0)
for (int i = 1; i <= n; i++) {
set_graph(graph, 0, i, 1);
}
// add edges incoming to sink(n+m+1 = total+1)
for (int i = n + 1; i <= total; i++) {
set_graph(graph, i, total + 1, 1);
}
int s, v;
for (int i = 0; i < n; i++) {
scanf("%d", &s);
for (int j = 0; j < s; j++) {
scanf("%d", &v);
set_graph(graph, i + 1, n + v, 1);
}
}
// source: 0, sink: total+1
// start
auto result = edmonds_karp(0, total +1, total +2, graph);
std::cout << result << "\n";
}즉, 이분 그래프의 왼쪽 정점들은 소가 되고, 오른쪽 정점들은 축사가 됩니다. 소의 수가 N이고 축사의 수가 M일 때, 소의 정점 번호는 1 ~ N으로 배정했으며, 축사의 정점 번호는 N+1 ~ N+M으로 배정했습니다. 그리고 source 정점은 0, sink 정점은 N+M+1로 배정하였습니다.
위 풀이의 시간복잡도는 \(O(|V||E|^2)\) 입니다. 하지만, 네트워크 유량에서 포드 풀커슨 알고리즘을 사용하면 \(O(|E|f)\)라는 것을 알고 있습니다(여기서 f는 최대 유량 값입니다). 따라서, 이분 매칭에서의 f는 최대 \(O(|V|)\)이므로, BFS가 아닌 DFS를 사용하여 포드 풀커슨 알고리즘을 구현하면 \(O(|V||E|)\)의 시간복잡도를 얻을 수 있습니다.
아래 코드는 포드 풀커슨 알고리즘으로 구현한 풀이입니다. DFS로 구현하기 위해 ford_fulkerson 함수와 dfs 함수를 따로 구현하여 main 함수에서 ford_fulkerson 함수를 호출합니다.
#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>
const int INF = 123456789;
void set_graph(std::vector<std::vector<int>>& graph, const int u, const int v, const int c)
{
graph[u][v] = c;
//graph[v][u] = -c;
}
int dfs(const int cur, const int capacity, const int sink, const int n, std::vector<std::vector<int>>& graph, std::vector<bool>& visited)
{
if (visited[cur])
return 0;
visited[cur] = true;
if (cur == sink)
return capacity;
for (int v = 0; v < n; v++) {
if (graph[cur][v] > 0) {
int cur_capacity = graph[cur][v];
if (capacity != 0 && cur_capacity > capacity) {
cur_capacity = capacity;
}
int f = dfs(v, cur_capacity, sink, n, graph, visited);
if (f) {
graph[cur][v] -= f;
graph[v][cur] += f;
return f;
}
}
}
return 0;
}
int ford_fulkerson(const int source, const int sink, const int n, std::vector<std::vector<int>>& graph)
{
std::vector<bool> visited(n, false);
int max_flow{}, cur_flow{};
while (1) {
fill(visited.begin(), visited.end(), false);
cur_flow = dfs(source, 0, sink, n, graph, visited);
if (cur_flow == 0)
break;
max_flow += cur_flow;
}
return max_flow;
}
int main(int argc, char* argv[])
{
std::vector<std::vector<int>> graph;
// set graph
int n{}, m{};
scanf("%d %d", &n, &m);
int total{}, e{};
total = n + m;
graph.resize(total +2, std::vector<int>(total +2, 0));
// add edges outgoing from source(0)
for (int i = 1; i <= n; i++) {
set_graph(graph, 0, i, 1);
}
// add edges incoming to sink(n+m+1 = total+1)
for (int i = n + 1; i <= total; i++) {
set_graph(graph, i, total + 1, 1);
}
int s, v;
for (int i = 0; i < n; i++) {
scanf("%d", &s);
for (int j = 0; j < s; j++) {
scanf("%d", &v);
set_graph(graph, i + 1, n + v, 1);
}
}
// source: 0, sink: n+1
// start
auto result = ford_fulkerson(0, total +1, total +2, graph);
std::cout << result << "\n";
}

결과를 살펴봐도 DFS를 사용한 포드 풀커슨 알고리즘 구현이 더 빠른 것을 볼 수 있습니다.
위에서 구현한 알고리즘은.... 네트워크 유량의 알고리즘을 그대로 사용했습니다.
https://blog.naver.com/kks227/220807541506
이분 매칭(Bipartite Matching)
이번에 올릴 글은 네트워크 플로우 개념의 연장...은 아닌 것 같고, 유량 그래프의 아주 특수하면서 메이저...
blog.naver.com
가끔 알고리즘에 대한 내용을 찾을 때 참고하는 블로그인데, 여기서 이분 매칭에 최적화된 구현을 보여주고 있습니다. 시간복잡도는 똑같이 \(O(|V||E|)\) 이지만... 코드가 훨씬 짧습니다... !
최적화된 풀이 방법은 위 포스팅에서 정말 잘 설명해주고 있기 때문에, 필요하시다면 참조 바랍니다 !
간단하게 설명하자면, 이분 그래프의 왼쪽 정점들을 순서대로 살펴보면서 매칭할 녀석들을 찾습니다(한 정점에서 dfs 함수 호출). 순차적으로 매칭되는 녀석들을 찾다가, 어느 정점(a)에서는 매칭 가능한 녀석(b)이 이미 다른 정점(c)과 매칭되어 있는 경우가 있습니다. 이런 경우에 포기하지 않고, 매칭 가능한 녀석(b)이랑 매칭되어 있는 다른 정점(c)가 매칭할 수 있는 또 다른 정점(d)을 찾아서 매칭시켜주고, (a)는 (b)랑 매칭시키게 됩니다. 즉, 기존에 (b)-(c)랑 매칭되어 있었지만, (c)가 다른 녀석 (d)와 매칭 가능한지 찾아서 (c)를 (d)와 매칭시켜주고, (a)는 (b)와 매칭시키는 방식입니다. 이런식으로 진행하며, 만약 더 이상 이런 방식이 불가능하면 dfs는 최종적으로 0을 리턴하게 됩니다.
저의 방식으로 최적화하여 구현한 코드는 다음과 같습니다.
#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>
const int INF = 123456789;
int dfs(int cur, std::vector<int>& match, std::vector<bool>& visited, const std::vector<std::vector<int>>& graph)
{
if (visited[cur])
return 0;
visited[cur] = true;
for (int v : graph[cur]) {
if (match[v] == -1 || dfs(match[v], match, visited, graph)) {
match[v] = cur;
return 1;
}
}
return 0;
}
int main(int argc, char* argv[])
{
int N, M;
scanf("%d %d", &N, &M);
int total = N + M;
std::vector<std::vector<int>> graph(total);
std::vector<int> match(total, -1);
int S, v;
for (int i = 0; i < N; i++) {
scanf("%d", &S);
for (int j = 0; j < S; j++) {
scanf("%d", &v);
graph[i].push_back(N + v - 1);
graph[N + v - 1].push_back(i);
}
}
std::vector<bool> visited(total, false);
int ret = 0;
for (int i = 0; i < N; i++) {
fill(visited.begin(), visited.end(), false);
ret += dfs(i, match, visited, graph);
}
std::cout << ret << "\n";
}
'Data Structure & Algorithm > 알고리즘' 카테고리의 다른 글
| NP-Complete Problems (1) (0) | 2022.04.23 |
|---|---|
| 강한 연결 요소 (Strongly Connected Component) (0) | 2022.04.22 |
| 포드 풀커슨 / 에드몬드 카프 알고리즘 (0) | 2022.04.20 |
| 선형 계획법과 치환 (3) - 쌍대성, 심플렉스법 (0) | 2022.04.19 |
| 선형 계획법과 치환 (2) - Network Flow, Bipartite Matching (0) | 2022.04.17 |




댓글