References
- Algorithm (Sanjoy Dasgupta)
Contents
- Flows in networks
- Max-flow Min-cut Theorem
- Bipartite Matching (이분 매칭)
선형 계획법과 치환 (1) - Examples of LP
선형 계획법과 치환 (1) - Examples of LP
References Algorithms (Sanjoy Dasgupta) Contents Introduction to Linear Programming Reduction (치환) Simplex Method 최단 경로나 최소 비용 신장 트리(cheapest spanning tree), 최장 증가 부분 수열(longe..
junstar92.tistory.com
지난 포스팅에 이어서 선형 계획법에 대해 계속 알아보도록 하겠습니다.
Flows in networks
Shipping oil

그림 (a)는 기름이 보내질 수 있는 파이프라인들의 네트워크를 표현한 유향 그래프입니다. 목표는 source(s)에서 sink(t)까지 가능한 많은 기름을 나르는 것입니다. 각 파이프라인은 처리할 수 있는 최대 용량을 가지며, 도중에 기름을 저장하기 위한 기회는 없습니다. 그림 (b)는 s에서 t까지 가능한 flow(유량)를 보여줍니다. 이것이 최선의 방법일까요?
Maximizing flow
여기서 다루는 네트워크들은 유향 그래프 G = (V, E)로 구성됩니다. 그래프 G는 source와 sink인 두 개의 특별한 노드 \(s, t \in V\)를 갖고 용량이 \(c_e > 0\)인 간선들을 갖습니다.
간선들의 용량을 초과하지 않고 s에서 t로 가능한 많은 기름을 보내야 합니다. 기름을 나르는 특정 방법을 flow(유량)이라 부르며 이는 네트워크의 각 간선 e에 대한 변수 \(f_e\)로 구성됩니다. 그리고 다음의 두 특성을 만족해야 합니다.
- 간선의 용량을 초과하지 않는다: \(0 \leq f_e \leq c_e\) for all \(e \in E\).
- s와 t를 제외한 모든 노드 u에 대하여, u로 들어오는 flow의 양은 u에서 나가는 양과 같다. 즉, flow는 보존됩니다.
\[\sum_{(w, u) \in E}f_{wu} = \sum_{(u,z) \in E}f_{uz}\]
flow의 크기는 s에서 t로 보내지는 총 양입니다. 그리고 보존 법칙에 의해 나가는 양과 같습니다.
\[\text{size}(f) = \sum_{(s,u)\inE}f_{su}\]
요약하자면, 목표는 선형 제약들을 만족하며 선형 목적 함수를 최대화하는 \(\{f_e : e \in E\}\)의 값들을 할당하는 것입니다. 그러나, 이는 선형계획법이며, maximum-flow 문제는 선형 계획법으로 풉니다.
최대 유량(maximum flow) 문제라고 부릅니다.
예를 들어, 그림 (a)의 네트워크에 대해 LP는 11개의 변수(간선당 하나)를 갖습니다. 그리고 총 27개의 제약을 만족하면서 \(f_{sa} + f_{sb} + f_{sc}\)를 최대화하는 값들을 찾습니다. 27개의 제약은 \(f_{sa} \geq 0\)과 같이 음이 아닌 제약 11개와 \(f_{sa} \geq 3\)과 같은 용량에 대한 제약 11개, 그리고 유량 보존(e.g., \(f_{sc} + f_{dc} = f_{ce}\))을 위한 5개의 제약입니다. 심플렉스법은 이 문제를 정확하게 해결하고, 이 예제에서 최대 유량이 7이라는 것을 금방 확인할 수 있습니다.
A closer look at the algorithm
지난 포스팅에서 알아봤던 심플렉스 알고리즘의 전부는 convex(볼록) feasible region의 표면에서 지역적인 이동을 계속 수행하여 최적의 솔루션에 도달할 때까지 목적 함수를 개선한다는 모호한 기하학적 직관에 불과합니다. 선형 계획법 포스팅 시리즈를 통해 심플렉스 알고리즘에 대해 더 자세히 공부해보면, 이 유량 LP를 어떻게 처리하는지 정확하게 이해할 수 있을 것입니다.
심플렉스 알고리즘의 동작은 다음과 같이 간단하게 해석된다는 사실을 알 수 있습니다.
- 0으로 시작
- s에서 t로 적절한 경로를 선택하고 이 간선들을 따라 유량을 최대한 증가시키는 것을 반복
아래 그림은 2번의 반복 후에 심플렉스 중단하는 작은 예제를 보여줍니다.
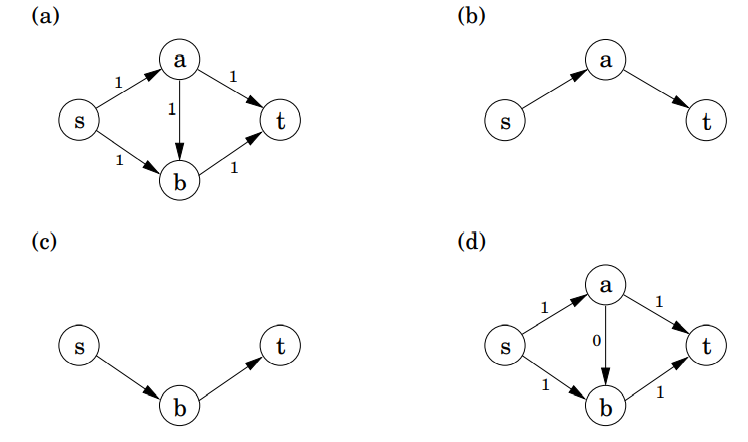
최종 유량은 2이며, 이 최적은 쉽게 알 수 있습니다.
여기에는 한 가지 복잡성이 있습니다.
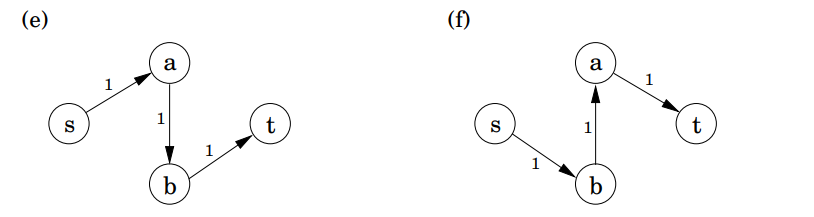
위의 그림 (e) 처럼 하나의 a-b 경로를 초기에 선택하면 어떨까요? 이 경로는 단지 하나의 유량 단위만 제공하지만 다른 모든 경로를 차단하는 것처럼 보입니다. 심플렉스는 기존 유량을 최소하도록 허용하여 이 문제를 해결합니다. (e)의 경우에는 (f)의 경로를 다음으로 선택합니다. 이 경로의 간선 (b, a)는 원래의 네트워크에는 없으며 간선 (a, b)에 할당된 유량을 취소하는 효과를 가집니다.
요약하면, 각 반복에서 심플렉스는 간선 (u, v)가 다음의 두 유형이 될 수 있는 s-t 경로를 찾습니다.
- (u, v)가 원래 네트워크에 존재하지만, 아직 전체 용량은 아니다.
- 역 간선 (v, u)는 원래의 네트워크에 있고, 이 간선 사이의 어떠한 유량이 있다.
만약 현재 유량이 f라면, 그때 첫 번째 경우에서 간선 (u, v)는 유량의 추가 단위 \(c_{uv} - f_{uv}\)까지 처리할 수 있도 두 번째 경우에는 추가 단위 \(f_{vu}\)((u, v) 상에 존재하는 유량의 전부 또는 일부를 취소)까지 다룹니다. 유량이 증가하는 기회들은 잔여 용량 \(c_f\)와 함께 정확히 두 가지 유형의 간선들이 나열된 잔여 네트워크 \(G^f = (V, E^f)\)에서 획득할 수 있습니다.

그리하여, 나머지 네트워크 내의 s-t 경로를 선택하는 것을 심플렉스와 동일하게 생각할 수 있습니다.
심플렉스의 동작을 시뮬레이션함으로써 최대 유량 문제를 해결하기 위한 알고리즘을 얻을 수 있습니다. 반복적으로 \(G^f\)를 구축할 때마다, 선형 시간의 BFS를 사용하여 \(G^f\)에서 적절한 s-t 경로를 찾고, 유량이 증가할 수 있는 경로가 더 이상 없으면 중단합니다.
아래 그림은 최대 유량 예제의 알고리즘을 설명해줍니다.


A certificate of optimality
놀라운 사실이 하나 있는데, 심플렉스는 최대 유량을 정확하게 계산할 뿐만 아니라 계산된 유량이 최적이라는 짧은 증거도 보여줍니다.
이것이 의미하는 바의 예제를 살펴보겠습니다. 위에서 살펴본 오일 네트워크의 노드를 L = {s,a,b}, R = {c,d,e,f}의 두 그룹으로 나눕니다.

전달되는 어떤 오일은 반드시 L에서 R로 전달되어야 합니다. 그러므로, 어떠한 유량도 L에서 R까지의 간선들의 총 용량을 초과하지 않습니다. 여기서 총 용량은 7입니다. 그러나 이는 크기가 7인 이전에 찾은 유량이 최적이어야 함을 의미합니다.
더 일반적으로 (s, t)-cut은 s가 L에 있고, t가 R에 있도록 정점들을 L과 R의 두 개의 분리된 그룹으로 분할합니다. 유량은 L에서 R까지의 간선의 총 용량이며 임의의 유량의 상한입니다.
- 임의의 유량 f와 임의의 (s, t)-cut (L, R)을 선택한다. 그때 size(f)는 capacity(L, R)보다 작거나 같다.
어떤 cut은 크며 느슨한 상한을 제공합니다. cut ({s, b, c}, {a, d, e, t})의 용량은 19입니다. 하지만 용량이 7인 cut도 있는데, 이것이 효율적인 최대 유량의 최적성 검증입니다. 단지 살펴본 예제에서 운이 좋아 7이 계산된 것이 아니며, 이와 같은 cut은 항상 존재합니다.
cut은 간단하게 말하면 그래프를 양분하는 것이며, 이전 포스팅(최소 신장 트리 (Minimum Spanning Tree))에서 간단하게 Cut Property에 대해 설명하고 있으니, 필요하시다면 참조바랍니다.
Max-flow Min-cut theorem
: 네트워크 내의 최대 유량의 크기는 가장 작은 (s, t)-cut의 용량과 같다.
게다가 이 알고리즘은 그 결과로 자동으로 이 cut을 발견합니다.
이것이 왜 참인지 살펴보겠습니다. f가 알고리즘을 종료했을 때 최종 유량이라고 가정해봅시다. 노드 t는 나머지 \(G^f\) 내의 s로부터 더 이상 접근할 수 없다는 것을 압니다. L이 \(G^f\)내의 s로부터 도달할 수 있는 노드들이라고 하고, R= V-L이 노드들의 나머지라고 합시다. 그때, (L, R)은 그래프 G의 cut입니다.

이때, size(f) = capacity(L, R) 이라고 주장할 수 있습니다.
이를 확인하기 위해, L이 정의되는 방법을 통해 살펴보겠습니다. L에서 R까지 가는 어떤 간선은 현재 유량 f 내에서 전체 용량이 되고 R에서 L까지 어떤 간선은 0의 유량을 가져야 합니다(따라서 예제에서 \(f_e = c_e\)이고, \(f_{e'} = 0\)입니다). 그리하여 (L, R) 사이의 net 유량은 정확히 cut의 용량입니다.
Efficiency
최대-유량 알고리즘의 각 반복은 효율적입니다. 만약 DFS나 BFS가 s-t 경로를 발견하기 위해 사용된다면 \(O(|E|)\)의 시간이 요구됩니다. 그렇다면 얼마나 많은 반복이 필요할까요?
원래의 네트워크 내의 모든 간선들이 C보다 작거나 같은 정수의 용량을 갖는다고 가정해봅시다. 이때 귀납적 인수는 알고리즘의 각 반복에서 유량이 항상 정수이고 정수 양만큼 증가한다는 것을 보여줍니다. 따라서 최대 유량은 기껏해야 \(C|E|\) (why?) 이기 때문에, 반복 횟수는 많아야 이정도 입니다. 다만 이는 안심할 수 있는 한계(bound)가 아닙니다. C가 만약 수백만 단위라면 어떻게 될까요?
만약 s-t의 경로들이 주의깊게 선택되지 않는다면, 반복의 수가 C에 비례하는 좋지 않은 경우가 발생하는 것이 가능합니다. 그러나 만약 세심한 방법(예를 들어 BFS를 사용하여 매우 적은 간선들을 사용해)으로 경로를 선택한다면, 이때 반복의 수는 용량에 무관하여 최대 \(O(|V|\cdot |E|)\)가 됩니다. 후자의 경우 전체 실행 시간은 최대 유량에 대해 \(O(|V| \cdot |E|^2)\)가 됩니다.
\(O(C|E|)\)의 시간 복잡도를 갖는 알고리즘이 포드 풀커슨 알고리즘(Ford-Fulkerson Algorithm)입니다. 그리고 BFS를 사용하여 최대 \(O(|V|\cdot |E|^2)\)의 시간 복잡도를 갖는 알고리즘은 에드몬드 카프 알고리즘(Edmonds-Karp Algorithm) 입니다. 이 알고리즘들에 대해서는 선형 계획법 포스팅을 마치고, 따로 살펴보도록 하겠습니다.
Bipartite Matching

위의 그림은 소년들(boys)를 표현하는 왼쪽 4개의 노드와 소녀들(girls)를 표현하는 오른쪽 4개의 노드들을 가진 그래프를 보여줍니다. 이렇게 모든 간선들이 그룹간 사이에 위치하여 노드들을 두 그룹으로 분할할 수 있는 그래프를 이분(bipartite)라고 합니다.
만약 이들이 서로 좋아한다면 소년과 소녀 사이에는 간선이 있습니다. 예를 들어, Al은 모든 소녀를 좋아합니다. 이때 모든 사람들이 그들이 좋아하는 어떤 사람과 파트너가 되도록 커플들을 선택하는 것이 가능할까요? 그래프-이론 용어로 Perfect Matching이 있을까요?
이러한 매칭(matchmaking) 게임은 최대 유량(maximum-flow) 문제로 축소되어 선형 계획법을 사용할 수 있습니다. 모든 소년들을 향해 나가는(outgoing) 간선들을 갖는 새로운 source 노드 s와 모든 소녀들로 들어가는(incoming) 간선들을 갖는 새로운 sink 노드 t를 만듭니다. 그리고 원래의 이분 그래프 내의 모든 간선들을 소년으로부터 소녀로 향하도록 지정합니다. 그리고 마지막으로 모든 간선의 용량을 1로 설정합니다. 이때, 이 네트워크가 커플 수와 동일한 크기를 갖는 유량(flow)를 갖는다면, perfect matching이 존재하게 됩니다.

실제로 상황은 방금 언급한 것보다 약간 더 복잡합니다. 알기 쉬운 것은 최적의 정수 값의 flow가 최적의 매칭에 해당한다는 것입니다. 예를 들어, Al-Carol 사이에 0.7 단위를 갖도록 하는 조금 손실되도록 해석된 flow가 될 수 있습니다. 다행히, 최대 유량 문제는 다음의 성질을 갖습니다.
- 만약 모든 간선의 용량이 정수라면, 이때 알고리즘에 의해서 발견되는 최적의 flow는 정수(integral)이다. 이는 알고리즘으로부터 직접 확인할 수 있으며, 이와 같은 경우에 각 반복에서 정수 양만큼 flow를 증가시킨다.
교재에서는 integral을 적분으로 해석하고 있는데... 아무래도 정수의 의미인 것으로 보입니다.
따라서 정수라는 조건은 maximum-flow 문제에서 자유롭게 사용됩니다. 하지만 불행히도 이는 규칙이 아닌 예외입니다. 나중에 NP-Complete 문제에 대한 내용도 살펴볼텐데, 만약 변수들이 정수일 것을 요구한다면 일반 선형 계획법의 최적 해답을 찾는 것은 매우 어려운 문제가 됩니다.
'Data Structure & Algorithm > 알고리즘' 카테고리의 다른 글
| 포드 풀커슨 / 에드몬드 카프 알고리즘 (0) | 2022.04.20 |
|---|---|
| 선형 계획법과 치환 (3) - 쌍대성, 심플렉스법 (0) | 2022.04.19 |
| 선형 계획법과 치환 (1) - Examples of LP (0) | 2022.04.16 |
| [DP] 외판원 문제 (Traverling Salseman Problem) (0) | 2022.04.15 |
| [DP] Knapsack Problem (0-1 Knapsack) (0) | 2022.04.14 |




댓글