References
- https://docs.opencv.org/
- OpenCV 4로 배우는 컴퓨터 비전과 머신러닝
Contents
- 소벨 필터, 샤르 필터
- 캐니 에지 검출기
- 직선 검출, 원 검출 (허프 변환)
에지(edge) 검출
미분과 그래디언트
영상에서 에지(edge)는 한쪽 방향으로 픽셀 값이 급격하게 바뀌는 부분을 의미합니다. 즉, 어두운 영역에서 갑자기 밝아지거나 또는 반대로 밝은 영역에서 급격하게 어두워지는 부분을 에지라고 합니다. 일반적으로 객체와 배경의 경계, 또는 객체와 다른 객체의 경계에서 에지가 발생합니다. 따라서 영상에서 에지를 찾아내는 작업은 객체의 윤곽을 알아낼 수 있는 유용한 방법이며 다양한 비전 시스템에서 객체 판별을 위한 전처리로 사용됩니다.
기본적으로 에지를 찾아내려면 픽셀 값의 변화율을 측정하여 변화율이 큰 픽셀을 선택해야 합니다. 수학에서 함수 또는 데이터의 변화율을 미분(derivative)이라고 하는데, 정확하게 이야기하면 함수의 미분이란 주어진 함수의 순간 변화율을 의미하고 1차원 연속 함수 \(f(x)\)의 미분은 다음과 같이 계산합니다.
\[f' = \frac{\mathrm{d} f}{\mathrm{d} x} = \lim_{\Delta x \rightarrow 0}\frac{f(x+\Delta x)-f(x)}{\Delta x}\]
위 수식에서 \(\Delta x\)는 x의 변화량을 의미합니다. 따라서, x의 변화량이 무한히 0에 가까워질 때의 함수 값의 변화량으라 미분이라고 합니다. 함수 값이 증가하는 위치에서의 함수의 미분 값은 0보다 큰 양수이며, 함수 값이 감소하는 위치에서의 함수의 미분 값은 0보다 작은 음수가 됩니다. 함수 값이 일정한 부분에서는 0이 됩니다.
미분에 관해서는 이미 잘 알고 있으리라 생각하고 넘어가도록 하겠습니다.
영상은 2차원 평면에서 정의된 함수이기 때문에 영상에서 에지를 찾기 위해서는 영상을 가로 방향과 세로 방향으로 각각 미분해야 합니다. 2차원 영상 \(I(x, y)\)를 가로 방향으로 미분한다는 것은 y 좌표는 고정한 상태에서 x축 방향으로만 미분 근사를 계산하는 것을 의미하며, 이러한 연산을 x축 방향으로의 편미분(partial derivative)라고 합니다. x축 방향의 편미분은 \(I_x\) 또는 \(\frac{\partial I}{\partial x}\)로 표기하고, 이와 유사하게 y축 방향으로의 편미분은 \(I_y\) 또는 \(\frac{\partial I}{\partial y}\)로 표기합니다. 2차원 영상 \(I(x, y)\)에 대하여 x, y축 방향에 대한 각각의 편미분을 중앙 차분(centered difference) 방법으로 근사화하면 다음과 같습니다.
\[\begin{matrix} I_x = \frac{\partial I}{\partial x} \approx \frac{I(x+1, y) - I(x-1, y)}{2} \\ \\ I_y = \frac{\partial I}{\partial y} \approx \frac{I(x, y+1) - I(x, y+1)}{2} \end{matrix}\]
중앙 차분을 이용한 영상의 미분 근사는 마스크 연산을 이용하여 쉽게 구현할 수 있으며, 2차원 영상을 x축과 y축 방향에 대해 편미분을 수행하는 필터 마스크는 아래와 같습니다.
왼쪽은 영상을 x축 방향으로 편미분을 수행하는 1x3 필터 마스크이고, 오른쪽은 y축 방향으로 편미분하는 3x1 필터 마스크입니다. 위에서 설명한 편미분 근사 수식을 그대로 적용하려면 필터 마스크 값에 1/2을 곱해야 하지만 보통 미분 값의 상대적 크기가 중요하기 때문에 위와 같이 단순화하여 사용합니다.
아래 코드는 입력 영상에 대해 각각의 방향에 대한 편미분 결과를 구하고, 화면에 출력합니다. 시각적으로 표현하기 위해 편미분한 결과에 128을 더해서 그레이스케일로 화면에 출력하도록 합니다.
#include <iostream>
#include "opencv2/opencv.hpp"
int main(int argc, char* argv[])
{
cv::Mat src = cv::imread("lena.bmp");
if (src.empty()) {
std::cout << "Image load failed!\n";
return -1;
}
cv::Mat mx = cv::Mat_<float>({ 1, 3 }, { -1 / 2.f, 0, 1 / 2.f });
cv::Mat my = cv::Mat_<float>({ 3, 1 }, { -1 / 2.f, 0, 1 / 2.f });
cv::Mat dx, dy;
cv::filter2D(src, dx, -1, mx, cv::Point(-1, -1), 128);
cv::filter2D(src, dy, -1, my, cv::Point(-1, -1), 128);
cv::imshow("src", src);
cv::imshow("dx", dx);
cv::imshow("dy", dy);
cv::waitKey();
cv::destroyAllWindows();
}실행 결과는 다음과 같습니다.
결과 영상에서 회색 영역은 입력 영상에서 픽셀 값 변화가 작은 영역이고, 흰색 또는 검은색으로 표현된 픽셀은 입력 영상에서 픽셀 값이 급격하게 바뀌는 부분입니다. 위 그림의 중앙에 있는 결과 영상에서 흰색으로 표현된 부분은 x좌표가 증가함에 따라 픽셀 값이 급격하게 커지는 위치이고, 검은색으로 표현된 부분은 픽셀 값이 급격하게 감소하는 위치입니다.
오른쪽 결과 영상에서는 y좌표가 증가함에 따른 픽셀 값이 크게 증가하거나 감소하는 부분이 흰색 또는 검은색으로 나타납니다.
2차원 공간의 영상에서 에지를 찾으려면 x축 방향과 y축 방향의 편미분을 모두 사용해야 합니다. 2차원 공간에서 정의된 함수 \(f(x, y)\)가 있을 때 이 함수의 x축 방향 미분과 y축 방향 미분을 한꺼번에 벡터로 그래디언트(gradient)라고 하고 다음과 같이 표기합니다.
\[\triangledown f = \begin{bmatrix} f_x \\ f_y \end{bmatrix} = f_x \textbf{\textsf{i}} + f_y \textbf{\textsf{j}}\]
그래디언트는 벡터이기 때문에 크기와 방향 성분으로 표현할 수 있으며, 그래디언트 벡터의 방향은 변화 정도가 가장 큰 방향을 나타내고, 크기는 변화율의 세기를 나타내는 척도입니다. 그래디언트 크기는 보통 \(\left \| \triangledown f \right \|\)로 표기하고, 다음과 같이 계산합니다.
\[\left \| \triangledown f \right \| = \sqrt{f_x^2 + f_y^2}\]
그래디언트 방향 \(\theta\)는 다음과 같이 계산됩니다.
\[\theta = tan^-1 \left ( \frac{f_y}{f_x}\right )\]
2차원 영상에서 에지를 찾는 기본적인 방법은 그래드언트 크기가 특정 값보다 큰 위치를 찾는 것인데, 여기서 에지 여부를 판단하기 위해 기준이 되는 값을 임계값(threshold)이라고 합니다. 보통 영상의 특성에 따라 임계값은 다르게 설정해야 하고, 보통 경험에 의해 결정됩니다. 일반적으로 임계값을 높게 설정하면 밝기 차이가 급격하게 변하는 에지 픽셀만 검출되고, 낮게 설정하면 약한 에지 성분도 검출됩니다.
마스크 기반 에지 검출
지금까지 영상을 x축, y축 방향으로 편미분하는 1x3 또는 3x1 크기의 마스크에 대해 알아봤습니다. 하지만 대부분의 영상에는 노이즈가 포함되어 있어서 이 마스크로 미분을 구할 경우 다소 정확하지 않은 결과가 나올 수 있습니다. 따라서 실제 영상에서 미분을 구할 때는 노이즈의 영향을 줄일 수 있도록 좀 더 큰 크기의 마스크를 이용합니다. 여러 가지 미분 근사 마스크가 있지만 그중 널리 사용되고 있는 미분 마스크는 소벨 필터(sobel filter) 마스크입니다.
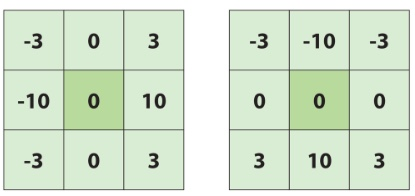
영상을 가로 방향과 세로 방향으로 미분하는 3x3 크기의 소벨 필터 마스크는 다음과 같습니다.
왼쪽 마스크는 x축 방향으로 편미분을 구하는 용도이며, 오른쪽은 y축 방향으로 편미분을 구하는 소벨 마스크입니다. 왼쪽 마스크는 현재 행에 대한 중앙 차분 연산을 2회 수행하고 이전 행과 다음 행에 대해서도 중앙 차분 연산을 1회씩 수행합니다. 이러한 연산은 현재 행과 이웃 행에서의 픽셀 값 변화가 유사하다는 특징을 이용하여 노이즈의 영향을 줄이기 위한 방법이며, 특히 현재 행에서 두 번의 미분 연산을 수행하는 것은 현재 행에 더 큰 가중치를 주기 위함입니다. y축 방향 미분을 구하는 것도 동일한 방식으로 동작합니다.
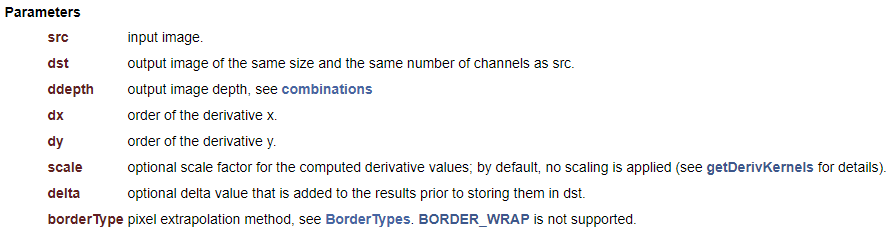
OpenCV에서는 소벨 마스크를 이용하여 영상을 미분하는 Sobel() 함수를 제공합니다. 이 함수는 3x3 소벨 마스크 또는 확장된 형태의 더 큰 마스크를 이용하여 영상을 미분합니다.
ddepth를 통해 결과 영상의 자료형을 명시적으로 지정해야 하며, -1을 지정하면 src와 같은 타입을 사용하는 dst 영상을 생성합니다. dx와 dy에는 각각 x축 방향과 y축 방향으로의 편미분 차수를 의미하며, Sobel() 함수에 의해 계산되는 결과 행렬 dst는 다음 수식과 같은 의미를 갖습니다.
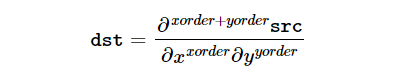
ksize 이후의 파라미터들은 모두 기본값을 가지고 있으므로 생략이 가능합니다. ksize에 1을 지정하면 3x1 또는 1x3 커널을 사용하고, 기본값인 3을 지정하면 3x3 소벨 마스크를 사용합니다.
이 함수를 이용하면 x, y축 방향으로의 고차 미분을 계산할 수도 있지만 보통 1차 미분을 구하는 용도로 사용됩니다.
아래 코드는 Sobel() 함수를 사용하여 각 방향으로의 미분 값을 계산하는 코드입니다.
#include <iostream>
#include "opencv2/opencv.hpp"
int main(int argc, char* argv[])
{
cv::Mat src = cv::imread("lena.bmp", cv::IMREAD_GRAYSCALE);
if (src.empty()) {
std::cout << "Image load failed!\n";
return -1;
}
cv::Mat dx, dy;
cv::Sobel(src, dx, -1, 1, 0, 3, 1, 128);
cv::Sobel(src, dy, -1, 0, 1, 3, 1, 128);
cv::imshow("src", src);
cv::imshow("dx", dx);
cv::imshow("dy", dy);
cv::waitKey();
cv::destroyAllWindows();
}
OpenCV에는 소벨 마스크 외에도 샤르 필터(Scharr filter) 마스크를 이용한 미분 연산도 지원합니다. 샤르 필터는 다음과 같습니다.
샤르 필터를 이용하여 영상을 미분하려면 Scharr() 함수를 사용합니다.
Sobel() 또는 Scharr() 함수를 이용하여 x 방향으로의 미분과 y 방향으로의 미분을 각각 계산하여 행렬에 저장한 후, 두 미분 행렬을 이용하여 그래디언트 크기를 계산할 수 있습니다. OpenCV는 2차원 벡터의 x방향 좌표와 y방향 좌표를 이용하여 벡터의 크기를 계산하는 magnitude() 함수를 제공하는데, 그 원형은 다음과 같습니다.
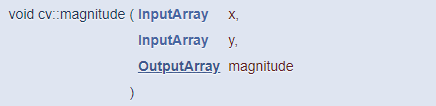
이 함수의 입력으로 사용되는 x와 y는 CV_32F 또는 CV_64F 타입의 행렬 또는 벡터이어야 합니다. magnitude() 함수의 출력 magnitude를 구성하는 원소 값은 다음 수식에 의해 계산됩니다.
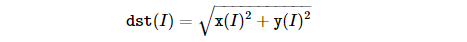
만약 x방향으로의 미분과 y방향으로의 미분이 저장된 두 개의 행렬이 있을 때, 그래디언트의 방향을 계산하고 싶다면 phase() 함수를 사용할 수 있습니다.
이 함수에서 x와 y는 입력이고, angle이 출력입니다. angle의 각 원소는 다음 수식에 의해 계산됩니다.
Sobel() 함수를 이용하여 실제 영상으로부터 그래디언트를 계산하고 그 크기를 이용하여 에지를 컴출하는 예제 코드는 다음과 같습니다.
#include <iostream>
#include "opencv2/opencv.hpp"
int main(int argc, char* argv[])
{
cv::Mat src = cv::imread("lena.bmp", cv::IMREAD_GRAYSCALE);
if (src.empty()) {
std::cout << "Image load failed!\n";
return -1;
}
cv::Mat dx, dy;
cv::Sobel(src, dx, CV_32FC1, 1, 0);
cv::Sobel(src, dy, CV_32FC1, 0, 1);
cv::Mat fmag, mag;
cv::magnitude(dx, dy, fmag);
fmag.convertTo(mag, CV_8UC1);
cv::Mat edge = mag > 150;
cv::imshow("src", src);
cv::imshow("mag", mag);
cv::imshow("edge", edge);
cv::waitKey();
cv::destroyAllWindows();
}위 코드에서 mag는 그래디언트 크기를 그레이스케일 영상 형식으로 나타낸 것인데, 만약 각 픽셀에서 계산된 그래디언트 크기가 255보다 큰 경우 포화 연산에 의해 흰색으로 표현됩니다. edge는 그래디언트 크기가 150보다 큰 픽셀은 흰색으로 그렇지 않은 픽셀을 검은색으로 표현된 이진 영상입니다. 만약 위 코드에서 사용한 임계값 150보다 낮은 값을 사용한다면 더 많은 에지가 검출됩니다.
캐니 에지 검출기
위에서 살펴본 방법들은 구현이 간단하고 바르게 동작하기 때문에 많이 사용됩니다. 하지만 그래디언트 크기만을 기준으로 에지를 검출하기 때문에 임계값에 민감하고 에지 픽셀이 두껍게 표현되는 문제점이 있습니다. 1986년 캐니(J. Canny)는 에지 검출을 최적화 문제 관점으로 접근하여 소벨 에지 검출의 단점을 해결할 수 있는 방법을 제시했습니다.
캐니는 논문에서 다음의 3가지 항목을 좋은 에지 검출기의 조건으로 언급했습니다.
- 정확한 검출
- 정확힌 위치
- 단일 에지 (하나의 에지는 하나의 점으로 표현되어야 함)
이러한 조건을 만족하는 에지 검출 방법을 캐니는 제시하였고, 이를 캐니 에지 검출기(canny edge detector)라고 합니다. 앞서 소개한 방법들이 단순히 그래디언트 크기만을 이용하여 에지를 찾는 방법이라면 캐니 에지 검출기는 그래디언트의 크기와 방향을 모두 고려하여 좀 더 정확한 에지 위치를 찾을 수 있습니다. 또한 에지는 서로 연결되어 있는 가능성이 높다는 점을 고려하여 그래디언트 크기가 다소 약하게 나타나는 에지도 놓치지 않고 찾을 수 있습니다.
캐니 에지 검출기는 내부적으로 아래의 4개의 연산 과정을 통해 수행됩니다.
- 가우시안 필터링
- 그래디언트 계산
- 비최대 억제(NMS, Non-Maxinum Suppression)
- 이중 임계값을 이용한 히스테리시스 에지 트래킹
가우시안 필터링
캐니 에지 검출기의 첫 번째 과정은 가우시안 필터링입니다. 이 단계가 첫 번째로 수행되는 이유는 영상에 포함된 노이즈를 제거하기 위함입니다. 다만 가우시안 필터링에 의해 영상의 에지 세기도 함께 감소할 수 있기 때문에 적절한 표준 편차를 선택하여 수행해야 합니다. 영상에 노이즈가 심하지 않다면 이 과정은 생략해도 됩니다.
그래디언트 계산
캐니 에지 검출기에서 그래디언트 계산은 보통 3x3 소벨 마스크를 사용합니다. 다만 앞서 살펴봤던 방법과는 달리 좀 더 정확한 에지를 찾기 위해 그래디언트 크기만 이용하는 것이 아닌 그래디언트 방향도 함께 고려합니다. 따라서 가로 방향과 세로 방향에 대해 각각 소벨 마스크 필터링을 수행한 후, 그래디언트 크기와 방향을 모두 계산해야 합니다.
2차원 공간에서 정의된 함수 \(f(x, y)\)의 그래디언트를 \(\bigtriangledown f = f_x \textbf{\textsf{i}} + f_y \textbf{\textsf{j}}\)라고 할 경우, 그래디언트 크기는 \(\left \| \triangledown f \right \| = \sqrt{f_x^2 + f_y^2}\)로 정의되고 이를 벡터 \(\bigtriangledown f\)의 L2 노름(L2 norm)이라고 합니다. 이때 그래디언트 크기를 계산할 때 연산 속도 향상을 위해 L1 노름(L1 norm)으로 계산하기도 하는데, L1 노름은 그래디언트 크기를 아래의 수식으로 계산합니다.
\[\left \| \bigtriangledown f \right \| \approx |f_x| + |f_y|\]
실제로 OpenCV에서 구현된 캐니 에지 검출기도 그래디언트 크기를 계산할 때 기본적으로 L1 노름을 사용합니다.
비최대 억제
에지 검출을 위해 단순히 그래디언트 크기가 특정 임계값보다 큰 픽셀을 선택할 경우, 에지 근방의 여러 픽셀이 한꺼번에 에지로 선택될 수 있습니다. 이렇게 에지가 두껍게 표현되는 현상을 방지하기 위해 캐니 에지 검출기에서는 비최대 억제(NMS, Non-Maximum Suppression) 과정을 이용합니다. NMS는 그래디언트 크기가 국지적 최대(local maximum)인 픽셀만을 에지 픽셀로 설정하는 기법이며, 상대적으로 국지적 최대가 아닌 픽셀은 에지 픽셀에서 제외됩니다.
일반적으로 2차원 영상에서의 local maximum을 찾으려면 특정 픽셀을 둘러싸고 있는 모든 픽셀 값을 검사하여 판단해야 하지만, 캐니 에지 검출기에서는 그래디언트 방향과 같은 방향에 있는 인접 픽셀들끼리만 NMS 검사를 수행합니다. 결과적으로 가장 변화율이 큰 위치의 픽셀만 에지로 검출되도록 합니다.
이중 임계값을 이용한 히스테리시스 에지 트래킹
캐니 에지 검출기에서는 두 개의 임계값을 사용합니다. 두 임계값 중 높은 임계값을 \(T_{\text{high}}\), 낮은 임계값을 \(T_{\text{low}}\)라고 표기한다면, 그래디언트 크기가 \(T_{\text{high}}\)보다 크다면 이 픽셀은 최종적으로 에지로 판단합니다. 만약 그래디언트 크기가 \(T_{\text{low}}\)보다 작으면 에지 픽셀이 아니라고 판단합니다. \(T_{\text{low}}\)와 \(T_{\text{high}}\)사이인 픽셀은 에지일 수도 있고 에지가 아닐 수도 있다고 판단하며, 이런 픽셀에 대해서는 추가 검사를 수행합니다.
캐니 에지 검출기의 마지막 단계에서는 히스테리시스 에지 트래킹(hysteresis edge tracking) 방법을 사용하여 \(T_{\text{low}}\)와 \(T_{\text{high}}\)사이인 픽셀 중에서 최종적으로 에지로 검출할 픽셀을 선택합니다. 이 방법은 에지 픽셀이 대체로 상호 연결되어 있다는 점을 이용합니다. 만약 이 픽셀인 \(T_{\text{high}}\)이상인 픽셀과 서로 연결되어 있다면 이 픽셀은 최종적으로 에지로 판단합니다. 반면 \(T_{\text{high}}\)이상인 픽셀과 연결되어 있지 않다면 최종적으로 에지가 아니라고 판단합니다.
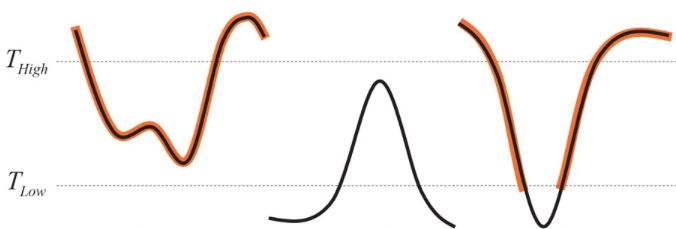
에지 트래킹의 동작을 이해하기 위해 위 그림을 살펴보겠습니다. 위 그림은 서로 연결되어 있는 에지 픽셀들의 그래디언트 크기를 표현하고 있습니다. 세 가지 형태의 에지 후보에 대하여 최종적으로 에지로 선택되는 픽셀들은 주황색으로 표시되어 있습니다. 중간에 있는 후보는 에지 픽셀이 \(T_{\text{high}}\)보다 큰 픽셀과 연결되어 있지 않으므로 최종 에지로 선택되지 않았습니다. 그리고 오른쪽에 있는 후보는 \(T_{\text{high}}\)보다 큰 픽셀과 연결되어 있어서 에지로 검출되지만 \(T_{\text{low}}\)보다 작은 픽셀은 에지로 판별하지 않는 것을 볼 수 있습니다.
OpenCV에서 캐니 에지 검출 알고리즘은 Canny() 함수에 구현되어 있습니다. Canny() 함수는 두 가지 형태로 정의되어 있습니다.
첫 번째 함수는 일반 영상을 입력으로 사용하여 에지를 검출할 때 사용하고, 두 번째 함수는 이미 x방향과 y방향의 미분 결과를 가지고 있을 때 사용합니다. Canny() 함수를 사용할 때에는 두 개의 임계값을 적절하게 지정하는 것이 중요한데, threshold1과 threshold2 인자에 지정하는 두 개의 임계값은 캐니 에지 검출기의 히스테리시스 에지 트래킹 단계에서 사용됩니다. 보통 낮은 임계값과 높은 임계값은 1:2 또는 1:3 비율로 지정합니다. apertureSize와 L2gradient 인자는 기본값이 있으므로 생략할 수 있습니다.
Canny() 함수를 이용하여 에지를 검출하는 코드는 다음과 같습니다.
#include <iostream>
#include "opencv2/opencv.hpp"
int main(int argc, char* argv[])
{
cv::Mat src = cv::imread("lena.bmp", cv::IMREAD_GRAYSCALE);
if (src.empty()) {
std::cout << "Image load failed!\n";
return -1;
}
cv::Mat dst1, dst2;
cv::Canny(src, dst1, 50, 100);
cv::Canny(src, dst2, 50, 150);
cv::imshow("src", src);
cv::imshow("dst1", dst1);
cv::imshow("dst2", dst2);
cv::waitKey();
cv::destroyAllWindows();
}dst1과 dst2는 서로 다른 임계값(100, 150)을 사용하여 에지를 검출합니다. 위 코드의 실행 결과는 다음과 같습니다.
직선과 원 검출
허프 변환 직선 검출
직선은 영상에서 찾을 수 있는 많은 특징 중 하나이며 영상을 분석하는데 중요한 정보를 제공합니다. 자율 주행 분야에서 차선을 검출하는 용도로 사용될 수도 있고, 수평이 맞지 않는 영상에서 수평선 또는 수직선 성분을 찾아내어 자동 영상 회전을 위한 정보로 사용할 수도 있습니다. 영상에서 직선 성분을 찾기 위해서는 우선 에지를 찾아내야 하고, 에지 픽셀들이 일직선상에 배열되어 있는지를 확인해야 합니다.
영상에서 직선을 찾기 위한 용도로 허프 변환(hough transform) 기법이 많이 사용됩니다. 허프 변환은 2차원 xy 좌표에서 직선의 방정식을 파라미터 공간으로 변환하여 직선을 찾는 알고리즘입니다.
일반적인 2차원 평면에서의 직선 방정식은 다음과 같이 나타낼 수 있습니다.
\[y = ax + b\]
이 수식에서 a는 기울기이고, b는 y 절편입니다. 이 직선 방정식은 가로축이 x, 세로축이 y인 2차원 xy 좌표 공간에서 정의되어 있으며, a와 b는 직선의 형태를 결정하는 파라미터입니다. 그런데 이 수식은 아래와 같이 바꿔 쓸 수 있습니다.
\[b = -xa + y\]
직선의 방정식을 위와 같이 변경하면, 마치 ab 좌표 공간에서 기울기가 -x이고 y 절편(b 절편)이 y인 직선의 방정식으로 보입니다. 이처럼 xy 공간에서의 직선 방정식을 ab 공간으로 변경하면 재미있는 현상이 발견됩니다. 바로 xy 공간에서 직선은 ab 공간에서 한 점으로 표현되고, 반대로 xy 공간에서의 한 점은 ab 공간에서 직선의 형태로 나타난다는 점입니다.
아래 그림은 xy 좌표 공간과 ab 좌표 공간과의 관계를 보여줍니다.
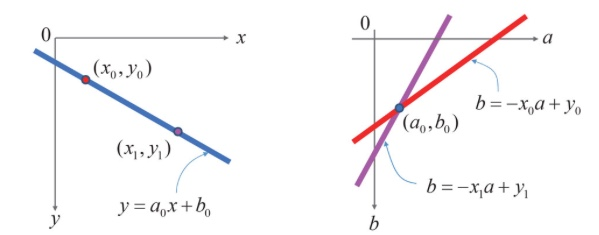
왼쪽 그래프에서 파란색 실선은 xy 공간에서 정의된 직선 \(y = a_0x + b_0\)입니다. 여기서 \(a_0, b_0\)는 직선의 모양을 결정하는 상수입니다. xy 공간에서 직선상의 한 점 \((x_0, y_0)\)를 선택한 뒤, 이 점의 좌표를 이용하면 ab 공간(오른쪽 그래프)에서 빨간색 직선 \(b = -x_0a + y_0\)을 정의할 수 있습니다. 마찬가지로 xy 공간에서 다른 한 점 \((x_1, y_1)\)를 이용하면 ab 공간에서의 보라색 직선 \(b = -x_1a + y_1\)을 표현할 수 있습니다. 이때 오른쪽 그래프에서 빨간색과 보란색 직선이 서로 교차하는 점의 좌표는 \((a_0, b_0)\)이며, 이는 xy 공간에서의 직선을 정의하는 두 개의 파라미터로 구성된 좌표입니다. 즉, xy 공간에서 파란색 직선상의 점을 이용하여 생성한 ab 공간상의 직선들은 모두 \((a_0, b_0)\)를 지나갑니다.
허프 변환을 이용하여 직선의 방정식을 찾으려면 xy 공간에서 에지로 판별된 모든 점을 이용하여 ab 파라미터 공간에 직선을 표현하고 직선이 많이 교차되는 좌표를 모두 찾아야 합니다. 이때 직선이 많이 교차하는 점을 찾기 위해 보통 축적 배열(accumulation array)을 사용하는데, 이 배열은 0으로 초기화된 2차원 배열에서 직선이 지나가는 위치의 배열 원소 값을 1씩 증가시켜 생성합니다.
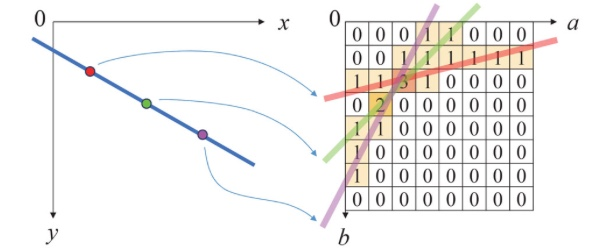
위 그림은 허프 변환에서 축적 배열을 구성하는 방법을 보여줍니다. 왼쪽 그래프(xy 공간)에서 직선 위 3개의 점을 선택했고, 각 점에 대응되는 ab 공간 상의 직선을 오른쪽 배열 위에 표현하고 있습니다. 그리고 배열 위에서 직선이 지나가는 위치의 원소 값을 1씩 증가시킵니다. 오른쪽 그래프에서의 배열이 축적 배열이며, 여기서 최댓값을 갖는 위치에 해당하는 a와 b 값이 xy 공간에 있는 파란색 직선의 방정식의 파라미터입니다. 위 그림은 하나의 직선에 대한 허프 변환을 보여주고 있으며, 여러 개의 직선이 존재하는 경우 축적 배열에서 여러 개의 local maximum 위치를 찾아서 직선의 방정식 파라미터를 결정할 수 있습니다.
다만, \(y = ax + b\) 꼴의 직선의 방정식을 사용하는 경우 모든 형태의 직선을 표현하기 어렵다는 단점이 있습니다. 대표적으로 y축과 평행한 수직선을 표현할 수 없는데, 수직선을 표현하려면 a의 값이 무한대가 되어야 하기 때문입니다. 따라서 실제 허프 변환을 구현할 때는 다음과 같이 극좌표계 골의 직선 방정식을 사용합니다.
\[xcos\theta + ysin\theta = \rho\]
위 수식에서 \(\rho\)는 원점에서 직선까지의 수직 거리를 나타내고, \(\theta\)는 원점에서 직선에 수직선을 내렸을 때 x축과 이루는 각도를 의미합니다. 이 경우 xy 공간에서 한 점은 \(\rho \theta\)공간에서 삼각함수 그래프 형태의 곡선으로 표현되고, \(\rho \theta\) 공간에서의 한 점은 xy 공간에서 직선으로 나타납니다. 극좌표계의 직선 방정식을 사용하여 허프 변환을 수행할 때도 축적 배열을 사용하고, 축적 배열에서 local maximum이 발생하는 위치에서의 \(\rho\)와 \(\theta\)값을 찾아 직선의 방정식을 구할 수 있습니다.
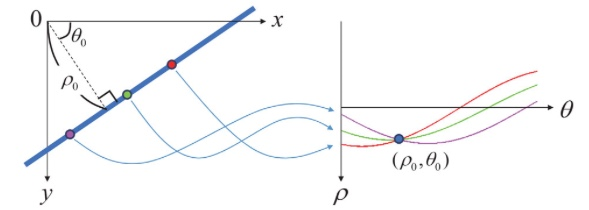
극좌표계 직선 방정식을 이용한 허프 변환 직선 검출 과정은 위의 그림과 같습니다. 왼쪽 그래프는 입력에서 사용하는 2차원 xy 좌표계이며, 파란색 직선은 극좌표계로 나타낸 직선 방정식입니다. 이 직선 위에 세 점을 선택하고, 각 점에 대응하는 \(\rho \theta\) 공간에서의 곡선을 오른쪽 그래프에서 보여주고 있습니다. 이 공간에서 세 곡선은 하나의 점에서 모두 교차하며, 이 점의 좌표 \(\rho_0, \theta_0\)가 왼쪽 그래프에서 파란색 직선을 나타내는 파라미터가 됩니다.
\(\rho\)와 \(\theta\)는 실수값을 가지기 때문에 C/C++ 코드로 축적 배열을 구현하려면 이들이 가질 수 있는 값의 범위를 적당한 크기로 나눠서 저장하는 양자화(quantization) 과정을 거쳐야 합니다. 예를 들어 \(\theta\)는 0부터 \(\pi\) 사이의 실수를 가질 수 있는데, 이 구간을 180단계로 나눌 수도 있고 360단계로 나눌 수도 있습니다. 구간을 촘촘하게 나누는 경우에는 입력에서 정밀한 직선 검출이 가능하지만 연산 시간이 늘어날 수 있는 반면, 구간을 너무 듬성하게 나눌 경우 연산은 빠르지만 검출의 정확도가 낮아질 수 있습니다.
OpenCV에서는 HoughLines() 함수를 사용하여 허프 변환 직선 검출을 수행할 수 있습니다.
HoughLines() 함수의 첫 번째 인자 image는 보통 Canny() 함수 등을 이용하여 구한 에지 영상을 지정합니다. HoughLines() 함수는 image 영상에서 0이 아닌 픽셀을 이용하여 축적 배열을 구성하는데, 직선 파라미터 정보를 받아 올 lines 인자에는 보통 vector<Vec2f> 또는 vector<Vec3f> 타입의 변수를 지정합니다. vector<Vec2f> 타입을 사용할 경우 \(\rho\)와 \(\theta\) 값이 저장되고, vector<Var3f> 타입을 사용하는 경우에는 축적 배열에서의 누적 값을 추가로 얻어 옵니다. rho와 theta에는 \(\rho\)와 \(\theta\) 값의 해상도를 조정하는 용도로 사용됩니다. 예를 들어, rho에 1을 지정하면 \(\rho\) 값을 1 픽셀 단위로 설정하며, theta에 CV_PI / 180을 지정하면 \(\theta\)를 \(1^{\circ}\)단위로 구분합니다. 즉, rho와 theta는 HoughLines() 함수 내부에서 사용할 축적 배열의 크기를 결정하는 역할을 합니다. threshold 인자에는 축적 배열에서 직선으로 판단할 임계값을 지정하며, 이 값이 작으면 더 많은 직선이 검출됩니다.
아래 코드는 HoughLines()를 이용하여 직선을 검출하는 예제 코드입니다. HoughLines() 함수를 사용하기 전에 Canny() 함수를 통해 에지 영상을 구하고, 이 영상을 HoughLines() 함수의 입력으로 사용합니다.
#include <iostream>
#include "opencv2/opencv.hpp"
int main(int argc, char* argv[])
{
cv::Mat src = cv::imread("building.jpg", cv::IMREAD_GRAYSCALE);
if (src.empty()) {
std::cout << "Image load failed!\n";
return -1;
}
cv::Mat edge;
cv::Canny(src, edge, 50, 150);
std::vector<cv::Vec2f> lines;
cv::HoughLines(edge, lines, 1, CV_PI / 180, 250);
cv::Mat dst;
cv::cvtColor(edge, dst, cv::COLOR_GRAY2BGR);
for (size_t i{ 0 }, size{ lines.size() }; i < size; i++) {
float r = lines[i][0], t = lines[i][1];
double cos_t = cos(t), sin_t = sin(t);
double x0 = r * cos_t, y0 = r * sin_t;
double alpha = 1000;
cv::Point pt1(cvRound(x0 + alpha * (-sin_t)), cvRound(y0 + alpha * cos_t));
cv::Point pt2(cvRound(x0 - alpha * (-sin_t)), cvRound(y0 - alpha * cos_t));
cv::line(dst, pt1, pt2, cv::Scalar(0, 0, 255), 2, cv::LINE_AA);
}
cv::imshow("src", src);
cv::imshow("dst", dst);
cv::waitKey();
cv::destroyAllWindows();
}위 코드의 실행 결과는 다음과 같습니다.
OpenCV는 기본적인 허프 변환 외에 확률적 허프 변환(probabilistic Hough transform)에 의한 직선 검출 방법도 제공하는데, 이 방법은 직선의 방정식 파라미터 \(\rho\)와 \(\theta\)를 반환하는 것이 아니라 직선의 시작점과 끝점 좌표를 반환합니다. 즉, 이 방법은 선분을 찾는 방법이며, OpenCV에서는 HoughLinesP() 함수에 구현되어 있습니다.
예제 코드는 다음과 같습니다.
#include <iostream>
#include "opencv2/opencv.hpp"
int main(int argc, char* argv[])
{
cv::Mat src = cv::imread("building.jpg", cv::IMREAD_GRAYSCALE);
if (src.empty()) {
std::cout << "Image load failed!\n";
return -1;
}
cv::Mat edge;
cv::Canny(src, edge, 50, 150);
std::vector<cv::Vec4i> lines;
cv::HoughLinesP(edge, lines, 1, CV_PI / 180, 160, 50, 5);
cv::Mat dst;
cv::cvtColor(edge, dst, cv::COLOR_GRAY2BGR);
for (size_t i{ 0 }, size{ lines.size() }; i < size; i++) {
cv::line(dst, cv::Point(lines[i][0], lines[i][1]), cv::Point(lines[i][2], lines[i][3]), cv::Scalar(0, 0, 255), 2, cv::LINE_AA);
}
cv::imshow("src", src);
cv::imshow("dst", dst);
cv::waitKey();
cv::destroyAllWindows();
}위 코드의 실행 결과는 다음과 같습니다.
허프 변환 원 검출
이번에는 허프 변환을 이용하여 영상에서 원을 검출하는 방법에 대해 살펴보겠습니다. 중심 좌표가 (a, b)이고 반지름이 r인 원의 방정식은 다음과 같습니다.
\[(x-a)^2 + (y-b)^2 = r^2\]
이러한 원의 방정식은 세 개의 파라미터를 가지고 있으므로, 허프 변환을 그대로 적용하려면 3차원 파라미터 공간에서 축적 배열을 정의하고 값이 큰 위치를 찾아야 합니다. 하지만 3차원 파라미터 공간에서 축적 배열을 정의하고 사용하려면 너무 많은 메모리와 연산 시간이 필요합니다. 따라서 OpenCV에서는 일반적은 허프 변환 대신 허프 그래디언트 방법(Hough gradient method)을 사용하여 원을 검출합니다.
이 방법은 두 가지 단계로 구성되는데, 첫 번째 단계에서는 영상에 존재하는 모든 원의 중심 좌표를 찾고, 두 번째 단계에서 검출된 원의 중심으로부터 원에 적합한 반지름을 구합니다. 원의 중심 좌표를 찾는 과정에서 축적 배열이 사용됩니다. 다만 허프 그래디언트 방법에서 사용하는 축적 배열은 파라미터 공간에서 만드는 것이 아니라 입력 영상과 동일한 xy 공간에서 2차원 배열로 만듭니다. 원의 중심을 찾기 위한 허프 그래디언트 방법은 입력의 모든 에지 픽셀에서 그래디언트를 구하고, 그래디언트 방향을 따르는 직선상의 축적 배열 값을 1씩 증가시킵니다.
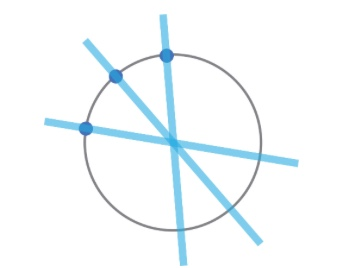
허프 그래디언트 방법은 위와 같습니다. 원주상의 모든 점에 대해 그래디언트 방향의 직선을 그리고, 직선상의 축적 배열 값을 증가시키면 결과적으로 원의 중심 위치에서 축적 배열 값이 크게 나타나게 됩니다. 일단 원의 중심을 찾은 후에는 다양한 반지름의 원에 대해 원주상에 충분히 많은 에지 픽셀이 존재하는지 확인하여 적절한 반지름을 선택합니다.
OpenCV에서는 HoughCircles() 함수를 사용하여 원을 검출할 수 있습니다.
위 함수의 image 파라미터에는 그레이스케일의 원본 영상을 전달합니다. HoughLines()나 HoughLinesP() 함수에서는 에지 영상을 전달했지만, HoughCircles()에는 에지가 아닌 원본의 그레이스케일 영상을 전달해야 합니다. 그러면 함수 내부에서 Sobel() 또는 Canny() 함수를 이용하여 그래디언트와 에지 영상을 계산한 후, 허프 그래디언트 방법으로 원을 검출합니다.
circles 인자에는 보통 vector<Vec3f> 또는 vector<Vec4f> 타입을 사용하는데, vector<Vec3f>를 사용하면 원의 중심 좌표 (a, b)와 반지름 r이 차례대로 저장되고, vector<Vec4f> 타입을 사용할 경우 추가로 축적 배열의 누적 값이 저장됩니다. dp 인자는 사용할 축적 배열의 크기를 결정하는 용도로 사용됩니다. 만약 dp를 1로 지정하면 입력 영상과 같은 크기로 축적 배열을 사용하고, 2를 지정하면 입력 영상의 가로/세로 크기를 2로 나눈 크기의 축적 배열을 사용합니다. minDist 인자에는 인접한 원의 최소 거리를 지정하는데, 두 원의 중심점 사이 거리거 minDist보다 작으면 두 원 중 하나는 검출하지 않게 됩니다.
param1 인자는 함수 내부에서 캐니 에지 검출기를 이용할 때 높은 임계값으로 사용되며, 낮은 임계값은 param1에 2를 나눈 값으로 설정합니다. param2는 축적 배열에서 원의 중심을 찾을 때 사용하는 임계값입니다. minRadius와 maxRadius 인자에는 검출할 원의 최소 반지름과 최대 반지름을 지정하며, 영상에서 검출할 원의 대략적인 크기를 알고 있다면 적절하게 지정함으로써 연산 속도를 향상시킬 수 있습니다.
HoughCircles() 함수를 사용하여 영상에서 원을 찾는 예제 코드는 다음과 같습니다.
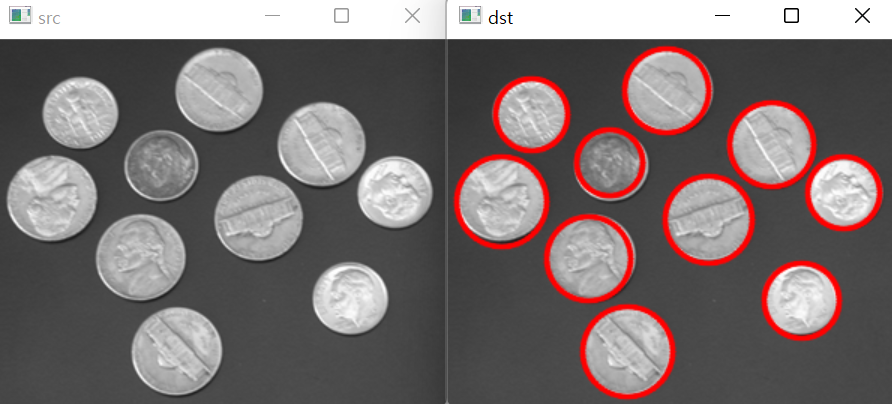
#include <iostream>
#include "opencv2/opencv.hpp"
int main(int argc, char* argv[])
{
cv::Mat src = cv::imread("coins.png", cv::IMREAD_GRAYSCALE);
if (src.empty()) {
std::cout << "Image load failed!\n";
return -1;
}
cv::Mat blurred;
cv::blur(src, blurred, cv::Size(3, 3));
std::vector<cv::Vec3f> circles;
cv::HoughCircles(blurred, circles, cv::HOUGH_GRADIENT, 1, 50, 150, 30);
cv::Mat dst;
cv::cvtColor(src, dst, cv::COLOR_GRAY2BGR);
for (auto& c : circles) {
cv::Point center(cvRound(c[0]), cvRound(c[1]));
int radius = cvRound(c[2]);
cv::circle(dst, center, radius, cv::Scalar(0, 0, 255), 2, cv::LINE_AA);
}
cv::imshow("src", src);
cv::imshow("dst", dst);
cv::waitKey();
cv::destroyAllWindows();
}HoughCircles를 호출할 때는 입력의 노이즈를 제거하기 위해 blur 함수를 적용한 이미지를 사용했고, 축적 배열의 크기는 입력과 동일한 크기를 사용하도록 지정했습니다. 그리고 두 원의 중심점 거리가 50픽셀보다 작으면 검출하지 않도록 지정했으며, 캐니 에지 검출기의 높은 임계값은 150으로 지정하고 축적 배열의 원소 값이 30보다 크면 원의 중심점으로 선택합니다.
위 코드의 실행 결과는 다음과 같습니다.
'프로그래밍 > OpenCV' 카테고리의 다른 글
| [OpenCV] 머신러닝과 KNearest 클래스 (0) | 2022.05.10 |
|---|---|
| [OpenCV] 컬러 이미지 처리 (0) | 2022.05.09 |
| [OpenCV] 어파인 변환 / 투시 변환 (0) | 2022.05.07 |
| [OpenCV] 영상 필터링 (0) | 2022.05.06 |
| [OpenCV] 영상 밝기/명암비, 히스토그램 (0) | 2022.05.05 |
댓글