References
- https://docs.opencv.org/
- OpenCV 4로 배우는 컴퓨터 비전과 머신러닝
Contents
- 어파인 변환
- 투시 변환
어파인 변환
영상의 기하하적 변환은 영상을 구성하는 픽셀의 배치 구조를 변경함으로써 전체 영상의 모양을 바꾸는 작업입니다. 이전 포스팅들에서 설명한 영상의 밝기, 명암비 조절, 필터링 등은 픽셀 위치는 고정한 상태에서 픽셀 값만 변경했지만, 기하학적 변환은 픽셀 값은 그대로 유지하면서 위치를 변경하는 작업입니다. 입력 영상에서 (x, y) 좌표의 픽셀을 결과 영상의 (x', y') 좌표로 변환하는 방법은 보통 아래의 고유 함수 형태로 나타낼 수 있습니다.
\[\begin{cases} x' = f_1(x, y) \\ y' = f_2(x, y) \end{cases}\]
위 수식에서 \(f_1, f_2\)는 각각 x와 y를 입력으로 받아 결과 영상에서의 픽셀 좌표를 출력하는 함수이며, 이 함수를 어떻게 정의하느냐에 따라 영상의 크기를 변경할 수도 있고 영상을 회전시킬 수도 있습니다. 또한 시점이 다른 위치에서 촬영된 것 같은 영상으로도 변경할 수 있습니다.
영상의 기하학적 변환 중에서 어파인 변환(affine transformation)은 영상을 평행 이동시키거나 회전, 크기 변환 등을 통해 만들 수 있는 변환을 통칭합니다. 영상에 어파인 변환을 적용하면 직선은 그대로 직선으로 나타나고, 직선 간의 길이 비율과 평행 관계는 그대로 유지됩니다. 직사각형 형태의 영상은 어파인 변환에 의해 평행사변형에 해당하는 모양으로 변경될 수 있습니다.
어파인 변환은 6개의 파라미터를 이용한 수식으로 정의할 수 있습니다. 어파인 변환에 의해 입력 영상의 좌표 (x, y)가 결과 영상의 좌표 (x', y')로 변환하는 수식은 다음과 같이 1차 다항식으로 표현합니다.
\[\begin{cases} x' = f_1(x, y) = ax + by + c \\ y' = f_2(x, y) = dx + ey + f \end{cases}\]
위 수식에서 a, b, c, d, e, f가 어파인 변환을 결정하는 파라미터입니다. 위처럼 2개의 수식으로 표현된 변환 식은 행렬을 이용해 다음과 같이 하나의 수식으로 변경할 수 있습니다.
\[\begin{bmatrix} x' \\ y ' \end{bmatrix} = \begin{bmatrix} a & b \\ d & e \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} + \begin{bmatrix} c \\ f \end{bmatrix}\]
그리고 수학적 편의를 위해 입력 영상의 좌표 (x, y)에 가상의 좌표 1을 추가하여 (x, y, 1) 형태로 바꾸면, 위의 행렬식을 다음과 같이 하나의 행렬 곱셈 형태로 바꿀 수 있습니다.
\[\begin{bmatrix} x' \\ y ' \end{bmatrix} = \begin{bmatrix} a & b & c\\ d & e & f \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix}\]
위 수식에서 여섯 개의 파라미터로 구성된 2x3 행렬을 어파인 변환 행렬이라고 부릅니다.
입력 영상과 어파인 변환 결과 영상으로부터 어파인 변환 행렬을 구하기 위해서는 최소 3점의 이동 관계를 알아야 합니다. 점 하나의 이동 관계로부터 x좌표와 y좌표에 대한 변환 수식 두 개를 얻을 수 있으므로, 점 3개의 이동 관계로부터 총 여섯 개의 방정식을 구할 수 있습니다. 따라서 점 3개의 이동 관계를 알고 있다면 여섯 개의 원소로 정의되는 어파인 변환 행렬을 구할 수 있습니다.
OpenCV는 어파인 변환 행렬을 구하는 함수와 어파인 변환 행렬을 이용하여 실제 영상에 어파인 변환을 수행하는 함수를 모두 제공합니다. 먼저 어파인 변환 행렬을 구하는 함수 이름은 getAffineTransform() 입니다.
Mat getAffineTransform( const Point2f src[], const Point2f dst[] );
Mat getAffineTransform( InputArray src, InputArray dst );이 함수는 src에 저장된 3개의 점을 dst에 저장된 점으로 옮기는 어파인 변환 행렬을 반환합니다. 점의 좌표를 담고 있는 src와 dst는 크기가 3인 Point2f 배열을 사용해도 되고, vector<Point2f>를 사용해도 됩니다. 이 함수가 반환하는 Mat 객체는 CV_64FC1 타입을 사용하는 2x3 크기의 어파인 변환 행렬입니다.
이렇게 어파인 변환 행렬을 구한 뒤에는 warpAffine() 함수를 사용하면 어파인 변환을 수행할 수 있습니다.


이 함수는 src를 어파인 변환하여 dst를 생성합니다. 이때 전달되는 어파인 변환 함수 M은 CV32FC1 또는 CV_64FC1 타입이어야 하고, 크기는 2x3 이어야 합니다. 어파인 결과 영상의 크기 dsize는 어파인 변환에 따라 사용자가 적절하게 지정해야 하며, Size()를 지정하면 입력과 동일한 크기의 결과 영상을 생성합니다.
3개의 점의 이동 관계로부터 어파인 변환 행렬을 구하고, 이를 이용하여 실제 영상을 어파인 변환하는 예제 코드는 다음과 같습니다.
#include <iostream>
#include "opencv2/opencv.hpp"
int main(int argc, char* argv[])
{
cv::Mat src = cv::imread("tekapo.bmp");
if (src.empty()) {
std::cout << "Image load failed!\n";
return -1;
}
cv::Point2f srcPts[3], dstPts[3];
srcPts[0] = cv::Point2f(0, 0);
srcPts[1] = cv::Point2f(src.cols - 1, 0);
srcPts[2] = cv::Point2f(src.cols - 1, src.rows - 1);
dstPts[0] = cv::Point2f(50, 50);
dstPts[1] = cv::Point2f(src.cols - 100, 100);
dstPts[2] = cv::Point2f(src.cols - 50, src.rows - 50);
cv::Mat M = cv::getAffineTransform(srcPts, dstPts);
cv::Mat dst;
cv::warpAffine(src, dst, M, cv::Size());
cv::imshow("src", src);
cv::imshow("dst", dst);
cv::waitKey();
cv::destroyAllWindows();
}위 코드의 실행 결과는 다음과 같습니다.

입력 영상에서 세 모서리 점이 지정한 위치로 적절하게 이동하였고, 결과 영상이 평행사변형 형태로 변환된 것을 확인할 수 있습니다.
참고로 어파인 변환 행렬이 있을 때, 영상 전체를 변환시키는 것이 아니라 일부 점들이 어느 위치로 이동하는지 알고 싶다면 transform() 함수를 사용할 수 있습니다.


예를 들어, 2x3 어파인 변환 행렬 M을 가지고 있고, (100, 20)과 (200, 50)이 어파인 변환 행렬에 의해 이동되는 위치를 알고 싶다면 다음과 같이 코드를 작성하면 됩니다.
std::vector<cv::Point2f> src = { cv::Point2f(100, 20), cv::Point2f(200, 50) };
std::vector<cv::Point2f> dst;
cv::transform(src, dst, M);
이동 변환
영상의 이동 변환(translation transformation)은 영상을 가로 또는 세로 방향으로 일정 크기만큼 이동시키는 연산을 의미하며 시프트(shift) 연산이라고도 합니다.
입력 영상의 모든 좌표를 x 방향으로 a만큼, y 방향으로 b만큼 이동하는 변환을 수식으로 나타내면 다음과 같습니다.
\[\begin{cases} x' = x + a \\ y' = y + b \end{cases}\]
위 수식을 행렬을 이용하면 다음과 같이 표현할 수 있습니다.
\[\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} + \begin{bmatrix} a \\ b \end{bmatrix}\]
위에서 (x, y) 좌표에 가상의 좌표 1을 더해서 하나의 2x3 행렬을 구성하면 이동 변환을 표현하는 어파인 변환 행렬을 만들 수 있습니다. 따라서, 영상을 x 방향으로 a만큼, y 방향으로 b만큼 이동하는 어파인 변환 행렬 M은 다음과 같이 표현할 수 있습니다.
\[M = \begin{bmatrix} 1 & 0 & a \\ 0 & 1 & b \end{bmatrix}\]
그리고 OpenCV에서 영상을 이동 변환하려면 위의 행렬 M을 만들고 이를 warpAffine() 함수 인자로 전달하면 됩니다.
다음은 예제 코드입니다. 아래 코드에서는 입력 영상을 가로로 150픽셀, 세로로 100픽셀만큼 이동시키고 그 결과를 출력합니다.
#include <iostream>
#include "opencv2/opencv.hpp"
int main(int argc, char* argv[])
{
cv::Mat src = cv::imread("tekapo.bmp");
if (src.empty()) {
std::cout << "Image load failed!\n";
return -1;
}
cv::Mat M = cv::Mat_<double>({ 2, 3 }, { 1, 0, 150, 0, 1, 100 });
cv::Mat dst;
cv::warpAffine(src, dst, M, cv::Size());
cv::imshow("src", src);
cv::imshow("dst", dst);
cv::waitKey();
cv::destroyAllWindows();
}위 코드의 실행 결과는 다음과 같습니다.
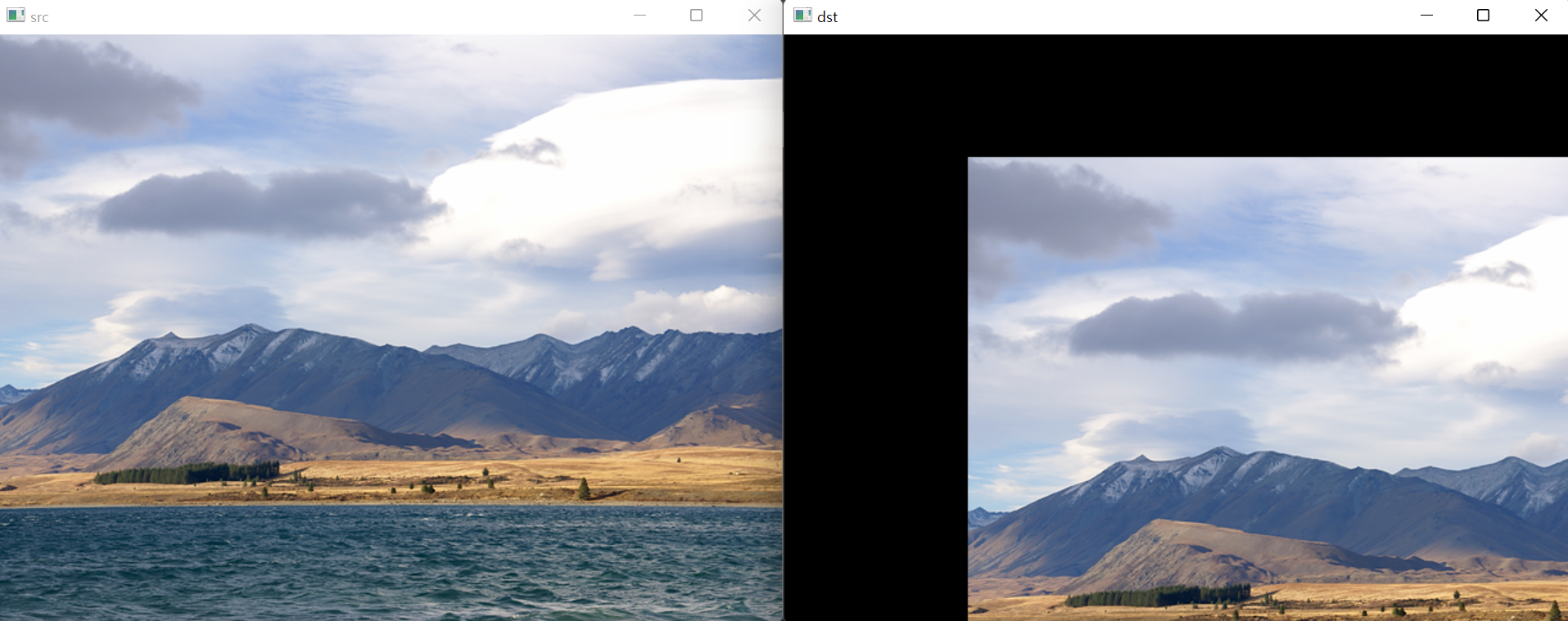
결과 영상에서 입력 영상이 (150, 100) 좌표부터 나타나는 것을 볼 수 있습니다. 그리고 입력 영상 픽셀 값이 복사되지 않은 영역은 검은색으로 채워져 있습니다.
전단 변환
전단 변환(shear transformation)은 직사각형 형태의 영상을 한쪽 방향으로 밀어서 평행사변형 모양으로 변환시킵니다. 전단 변환은 가로 방향 또는 세로 방향으로 각각 정의할 수 있습니다. 전단 변환은 영상의 픽셀을 가로 방향 또는 세로 방향으로 이동시키지만, 픽셀이 어느 위치에 있느냐에 따라 이동 정도가 달라집니다.
아래 수식은 y 좌표가 증가함에 따라 영상을 가로 방향으로 조금씩 밀어서 만드는 전단 변환 수식입니다.
\[\begin{matrix} \begin{cases} x' &= x + m_x y \\ y' &= y \end{cases}& or & \begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} 1 & m_x \\ 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} + \begin{bmatrix} 0 \\ 0 \end{bmatrix} \end{matrix}\]
그리고 x 좌표가 증가함에 따라 영상을 세로 방향으로 조금씩 밀어서 만드는 전단 변환 수식은 다음과 같습니다.
\[\begin{matrix} \begin{cases} x' &= x \\ y' &= m_y y + y \end{cases}& or & \begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ m_y & 1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} + \begin{bmatrix} 0 \\ 0 \end{bmatrix} \end{matrix}\]
위의 두 수식에서 \(m_x\)와 \(m_y\)는 영상으로 각각 가로 방향과 세로 방향으로 밀림 정도를 나타내는 실수입니다. 결국 전단 변환을 나타내는 2x3 어파인 변환 행렬 M은 다음과 같이 나타낼 수 있습니다.
\[\begin{matrix} M = \begin{bmatrix} 1 & m_x & 0 \\ 0 & 1 & 0 \end{bmatrix} & or & M = \begin{bmatrix} 1 & 0 & 0 \\ m_y & 1 & 0 \end{bmatrix} \end{matrix}\]
전단 변환을 수행하는 2x3 변환 행렬을 생성하여 영상을 전단 변환하는 예제 코드는 다음과 같습니다. 아래 코드에서 출력 영상의 일부가 잘리지 않도록 적절하게 가로 크기를 cvRound(src.cols + src.rows * mx)로 지정했습니다.
#include <iostream>
#include "opencv2/opencv.hpp"
int main(int argc, char* argv[])
{
cv::Mat src = cv::imread("tekapo.bmp");
if (src.empty()) {
std::cout << "Image load failed!\n";
return -1;
}
double mx = 0.3;
cv::Mat M = cv::Mat_<double>({ 2, 3 }, { 1, mx, 0, 0, 1, 0 });
cv::Mat dst;
cv::warpAffine(src, dst, M, cv::Size(cvRound(src.cols + src.rows * mx), src.rows));
cv::imshow("src", src);
cv::imshow("dst", dst);
cv::waitKey();
cv::destroyAllWindows();
}위 코드의 실행 결과는 다음과 같습니다.
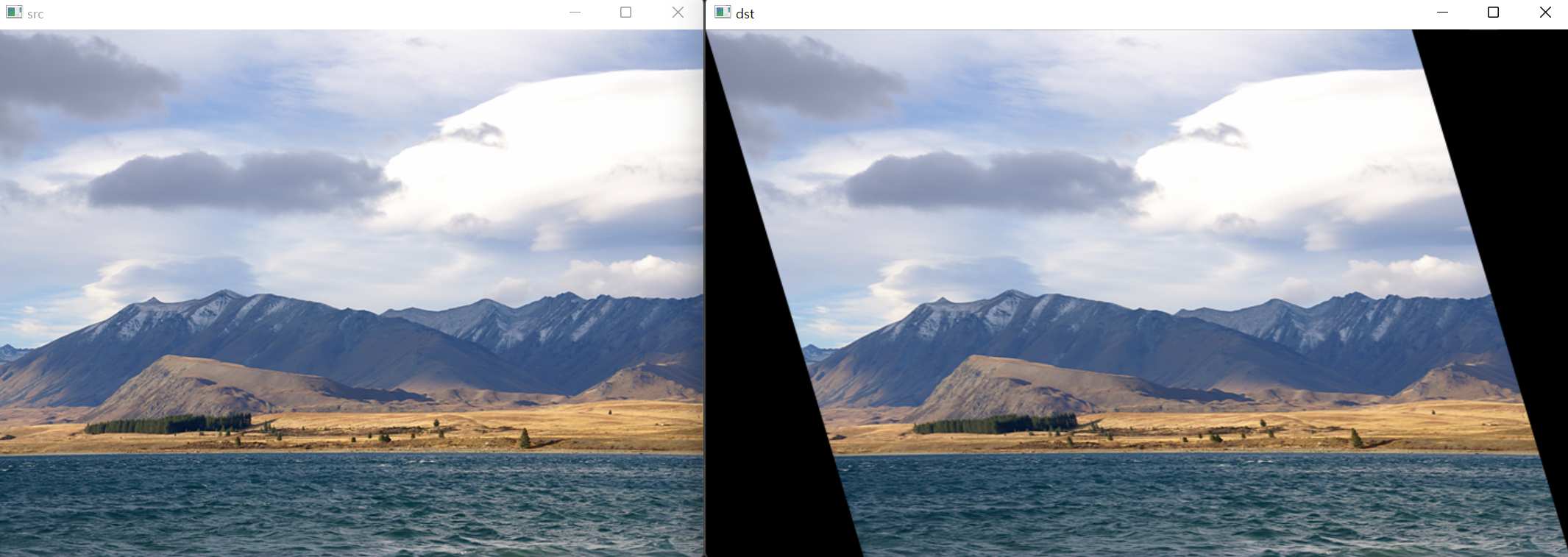
크기 변환
영상의 크기 변환(scale transformation)은 영상의 전체적인 크기를 확대 또는 축소하는 변환입니다. 컴퓨터 비전에서 영상의 크기를 변경하는 작업은 매우 자주 발생하는데, 예를 들어 몇몇 인식 시스템은 정해진 크기의 영상만을 입력으로 전달 받기 때문에 영상을 해당 크기에 맞게 변경하여 입력으로 전달해야 합니다. 또는 복잡한 알고리즘을 수행하기 전에 앞서 연산 시간을 단축하기 위하여 입력 영상의 크기를 줄여서 사용하는 경우도 있습니다.
영상의 크기 변환을 그림으로 표현하면 다음과 같습니다.
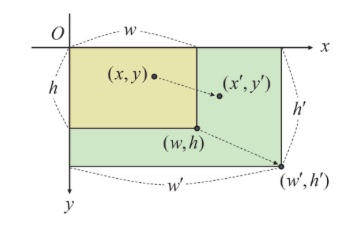
위 이미지에서 노란색 사각형 영역은 크기가 wh인 원본 영상이고, 녹색 사각형 영역은 크기가 w'h'로 확대된 결과 영상입니다. 원본 영상의 가로 픽셀 크기가 w이고 결과 영상의 가로 크기가 w'이기 때문에 가로 방향으로의 크기 변환 비율 \(s_x = \frac{w'}{w}\)로 계산할 수 있습니다. 마찬가지로 y 방향으로의 크기 변환 비율은 \(s_y = \frac{h'}{h}\)로 계산됩니다. 따라서 입력 영상의 좌표 (x, y)로부터 크기 변환 결과 영상의 좌표 (x', y')는 다음의 수식으로 계산할 수 있습니다.
\[\begin{matrix} \begin{cases} x' = s_x x \\ y' = s_y y \end{cases} & or & \begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} s_x & 0 \\ 0 & x_y \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} + \begin{bmatrix} 0 \\ 0 \end{bmatrix} \end{matrix}\]
위 수식에서 \(s_x\) 또는 \(s_y\)가 1보다 크면 영상이 확대되고, 1보다 작으면 축소됩니다.
영상의 크기 변환을 나타내는 어파인 변환 행렬 M은 다음과 같습니다.
\[M = \begin{bmatrix} s_x & 0 & 0 \\ 0 & s_y & 0 \end{bmatrix}\]
따라서 위와 같은 어파인 변환 행렬을 생성하고 warpAffine() 함수를 이용하면 영상의 크기 변환을 수행할 수 있습니다. 하지만 영상의 크기를 변환하는 작업은 실제 영상 처리 시스템에서 매우 빈번하기 때문에 보다 간단하게 크기를 변경할 수 있는 resize() 함수를 제공합니다.

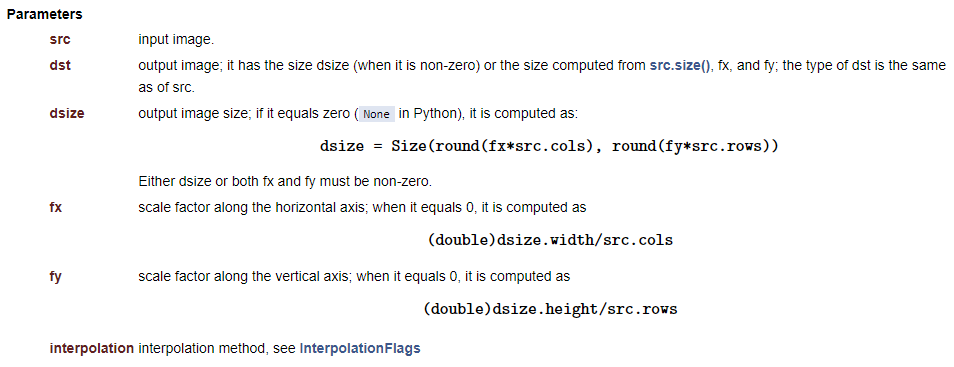
이 함수는 src를 dsize 크기로 확대 또는 축소한 dst 영상을 생성합니다. 결과 영상의 크기는 dsize 인자를 통해 명시적으로 지정할 수도 있고, 또는 가로 방향 및 세로 방향으로의 크기 변환 비율인 fx와 fy 값을 통해 지정할 수도 있습니다. 만약 결과 영상의 크기를 픽셀 단위로 지정하여 크기 변환을 수행하려면 dsize에 0이 아닌 값을 지정하고, fx와 fy는 0으로 설정합니다. 반대로 입력 영상 크기를 기준으로 변환 비율을 지정하여 변환하려면 dsize에는 Size()를 지정하고 fx와 fy에는 0이 아닌 양의 실수를 지정합니다.
resize() 함수 파라미터 중 interpolation에는 보간법(interpolation) 알고리즘을 나타내는 InterpolationFlags 열거형 상수를 지정합니다. 보간법은 결과 영상의 픽셀 값을 결정하기 위해 입력 영상에서 주변 픽셀 값을 이용하는 방식을 의미하며, resize() 함수에서는 아래의 표에 나타난 알고리즘을 사용할 수 있습니다.
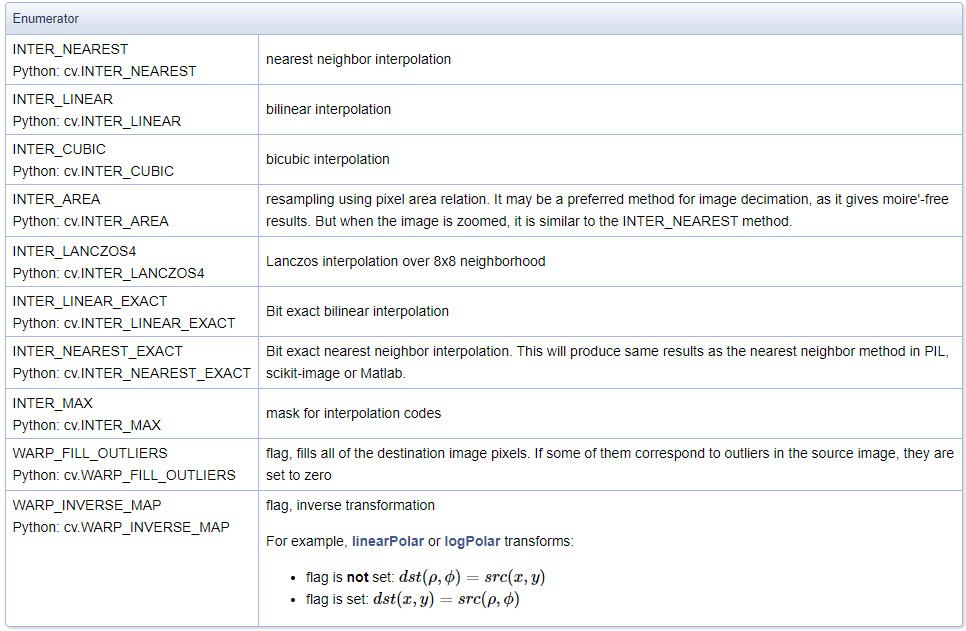
INTER_NEAREST 방법은 가장 빠르게 동작하지만 결과 영상의 화질이 좋지 않으며, INTER_LINEAR 방법은 연산 속도도 빠르고 화질도 충분히 좋은 편이라고 많이 사용됩니다. INTER_LINEAR보다 더 좋은 화질을 원한다면 INTER_CUBIC 또는 INTER_LANCZOS4를 사용하는 것이 좋습니다. 영상을 축소하는 경우 INTER_AREA 방법을 사용하면 무아레 현상이 적게 발생하며 화질 면에서 유리합니다.
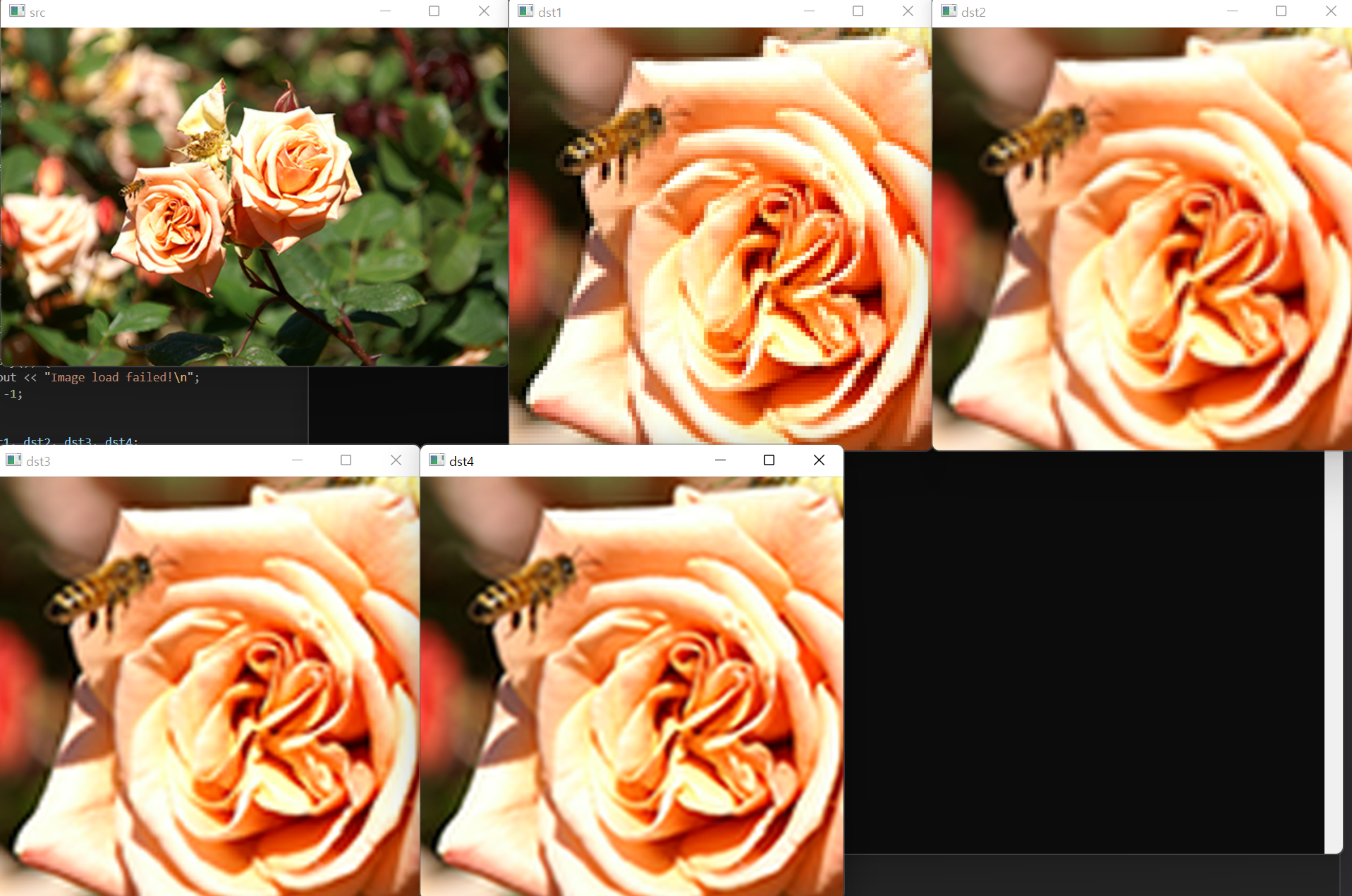
resize() 함수와 다양한 보간법을 이용하여 영상을 확대하는 예제 코드는 다음과 같습니다. 480x320 크기의 이미지를 1920x1080 크기로 확대하고, 확대한 결과의 일부를 출력합니다.
#include <iostream>
#include "opencv2/opencv.hpp"
int main(int argc, char* argv[])
{
cv::Mat src = cv::imread("rose.bmp");
if (src.empty()) {
std::cout << "Image load failed!\n";
return -1;
}
cv::Mat dst1, dst2, dst3, dst4;
cv::resize(src, dst1, cv::Size(), 4, 4, cv::INTER_NEAREST);
cv::resize(src, dst2, cv::Size(1920, 1280));
cv::resize(src, dst3, cv::Size(1920, 1280), 0, 0, cv::INTER_CUBIC);
cv::resize(src, dst4, cv::Size(1920, 1280), 0, 0, cv::INTER_LANCZOS4);
cv::imshow("src", src);
cv::imshow("dst1", dst1(cv::Rect(400, 500, 400, 400)));
cv::imshow("dst2", dst2(cv::Rect(400, 500, 400, 400)));
cv::imshow("dst3", dst3(cv::Rect(400, 500, 400, 400)));
cv::imshow("dst4", dst4(cv::Rect(400, 500, 400, 400)));
cv::waitKey();
cv::destroyAllWindows();
}위 코드 실행 결과는 다음과 같습니다.
회전 변환
영상 처리 시스템에서 입력 영상을 회전해야 하는 경우도 종종 발생합니다. 예를 들어, OCR 시스템의 경우 보통 글씨 이미지가 수평이 맞아야 인식률이 증가하므로 문서의 회전 각도를 측정하여 영상을 적절하게 회전한 후 OCR 시스템 ㅇ비력으로 사용하는 것이 좋습니다.
영상의 회전 변환(rotation transformation)은 특정 좌표를 기준으로 영상을 원하는 각도만큼 회전하는 변환입니다. 원점을 기준으로 영상을 반시계 방향으로 \(\theta\)만큼 회전하는 변환을 그림으로 나타내면 다음과 같습니다.
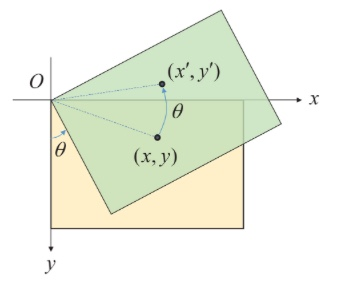
영상의 회전 변환에 의해 입력 영상의 점 (x, y)가 이동하는 점의 좌표 (x', y')는 다음과 같이 삼각함수를 이용하여 구할 수 있습니다.
\[\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} cos\theta & sin\theta \\ -sin\theta & cos\theta \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} + \begin{bmatrix} 0 \\ 0 \end{bmatrix}\]
따라서 영상을 반시계 방향으로 \(\theta\)만큼 회전하는 어파인 변환 행렬은 다음과 같이 정의됩니다.
\[M = \begin{bmatrix} cos\theta & sin\theta & 0 \\ -sin\theta & cos\theta & 0 \end{bmatrix}\]
따라서 위의 행렬을 가지고 warpAffine() 함수를 사용하면 영상을 회전시킬 수 있습니다.
다만, 영상을 회전하는 경우도 빈번하여 OpenCV에서는 영상의 회전을 위한 어파인 변환 행렬을 생성하는 getRotationMatrix2D() 함수를 제공합니다.


이 함수는 center 점을 기준으로 반시계 방향으로 angle 각도만큼 회전한 후, scale 크기만큼 확대 또는 축소하는 2x3 어파인 변환 행렬을 반환합니다. 만약 시계 방향으로 회전하는 어파인 변환 행렬을 구하고 싶다면 angle에 음수를 지정합니다. 이 함수가 반환하는 어파인 변환 행렬은 다음과 같습니다.

이 함수를 이용하여 어파인 변환 행렬을 구하고 영상을 회전시키는 예제 코드는 다음과 같습니다. 이 코드는 원본 영상의 중심을 기준으로 반시계 방향으로 20도만큼 회전시키고 그 결과를 화면에 출력합니다.
#include <iostream>
#include "opencv2/opencv.hpp"
int main(int argc, char* argv[])
{
cv::Mat src = cv::imread("tekapo.bmp");
if (src.empty()) {
std::cout << "Image load failed!\n";
return -1;
}
cv::Point2f cp(src.cols / 2.f, src.rows / 2.f);
cv::Mat M = cv::getRotationMatrix2D(cp, 20, 1);
cv::Mat dst;
cv::warpAffine(src, dst, M, cv::Size());
cv::imshow("src", src);
cv::imshow("dst", dst);
cv::waitKey();
cv::destroyAllWindows();
}위 코드의 실행 결과는 다음과 같습니다.
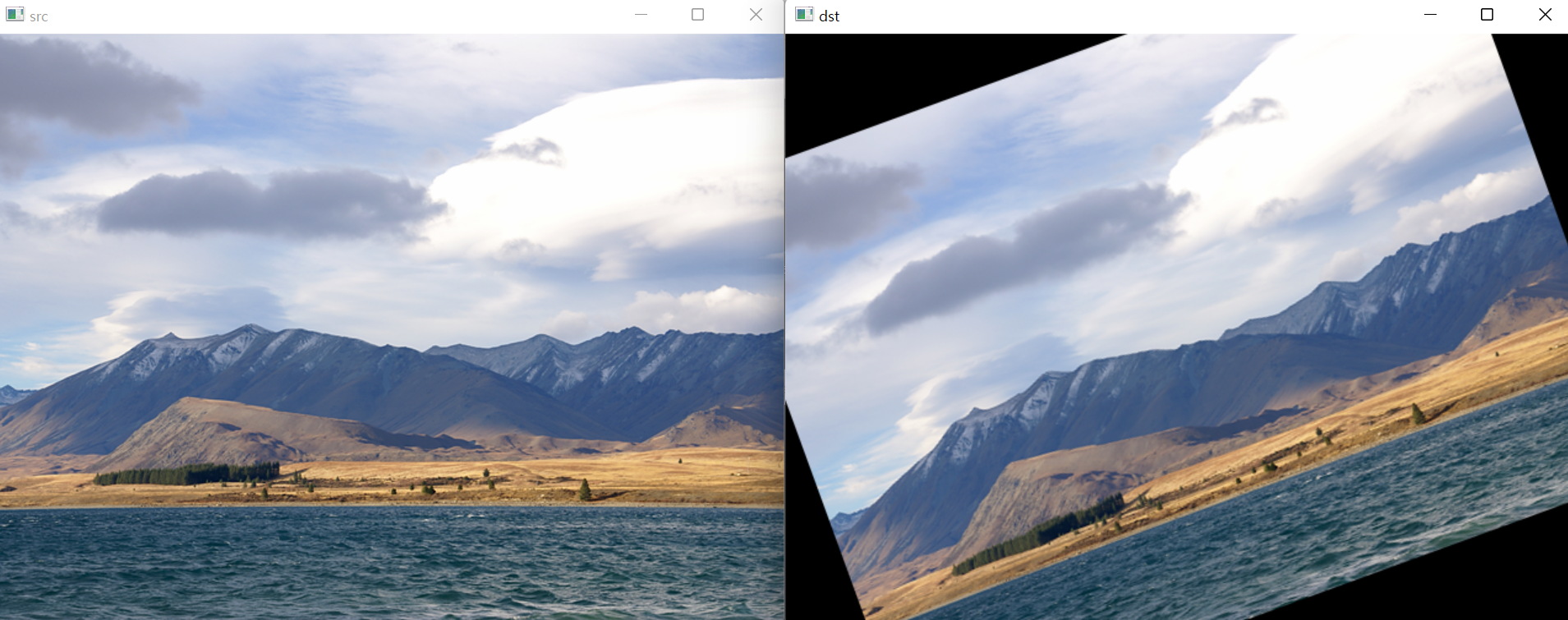
참고로 직사각형 형태의 영상을 회전하면 영상의 일부가 나타나지 않을 수 있으므로 잘리기 않게 하려면 결과 영상의 크기를 더 크게 설정하고 회전과 이동 변환을 함께 고려해야 합니다.
그리고 OpenCV에서 영상을 90도 단위로 회전하고 싶은 경우에는 rotate() 함수를 사용할 수 있습니다.
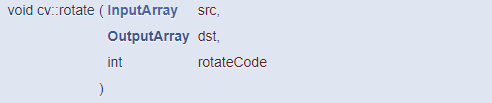

위 함수의 세 번째 파라미터 rotateCode에 ROTATE_90_CLOCKWISE를 지정하면 반시계 방향으로 90도 회전하고, ROTATE_90_COUNTERCLOCKWISE를 지정하면 반시계 방향으로 90도 회전합니다.
대칭 변환
영상의 대칭 변환에 의한 좌표 변환 수식은 다음과 같습니다. 여기서 w는 입력 영상의 가로 크기입니다.
\[\begin{cases} x' &= w-1-x \\ y' &= y \end{cases}\]
위 수식을 정리해서 행렬 형태로 바꾸면 다음과 같습니다.
\[\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} -1 & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} + \begin{bmatrix} w-1 \\ 0 \end{bmatrix}\]
위의 수식을 정리해서 보면, 좌우 대칭 영상을 x축 방향으로 -1배 크기 변환한 후 x축 방향으로 w-1만큼 이동한 것과 같습니다. 따라서 좌우 대칭 변환도 어파인 변환의 하나입니다.
영상의 상하 대칭 변환도 비슷한 방식으로 계산되며, 수식으로 정리하면 다음과 같습니다.
\[\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} + \begin{bmatrix} 0 \\ h-1 \end{bmatrix}\]
여기서 h는 입력 영상의 세로 크기입니다.
OpenCV는 영상의 대칭 변환을 수행하는 flip() 함수를 제공합니다. 이 함수는 영상을 가로 방향, 세로 방향, 또는 가로와 세로 양 방향에 대해 대칭 변환한 영상을 생성합니다.
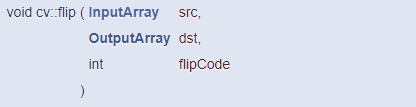

대칭 방법은 flipCode의 부호에 따라 결정됩니다. 일반적으로 좌우로 대칭 변환하려면 flipCode에 1을 지정하고, 상하로 대칭 변환하려면 0을 지정합니다. 그리고 상하좌우 모두 수행하려면 -1을 지정합니다.
flip() 함수를 이용하여 대칭 변환을 수행하는 예제 코드는 다음과 같습니다.
#include <iostream>
#include "opencv2/opencv.hpp"
int main(int argc, char* argv[])
{
cv::Mat src = cv::imread("eastsea.bmp");
if (src.empty()) {
std::cout << "Image load failed!\n";
return -1;
}
cv::imshow("src", src);
cv::Mat dst;
int flipCode[] = { 1, 0, -1 };
for (int i = 0; i < 3; i++) {
cv::flip(src, dst, flipCode[i]);
cv::String text = cv::format("flipCode: %d", flipCode[i]);
cv::putText(dst, text, cv::Point(10, 30), cv::FONT_HERSHEY_SIMPLEX, 1.0, cv::Scalar(255, 0, 0), 1, cv::LINE_AA);
cv::imshow("dst", dst);
cv::waitKey();
}
cv::destroyAllWindows();
}위 코드의 실행 결과는 다음과 같습니다.

투시 변환
어파인 변환보다 자유도가 높은 투시 변환(perspective transformation)은 직사각형 형태의 영상을 임의의 볼록 사각형 형태로 변경할 수 있는 변환입니다. 투시 변환에 의해 원본 영상에 있던 직선은 결과 영상에서도 직선성이 그대로 유지되지만, 두 직선의 평행 관계는 깨질 수 있습니다.
아래 그림은 4개의 점의 이동 관계에 의해 결정되는 투시 변환을 보여줍니다.
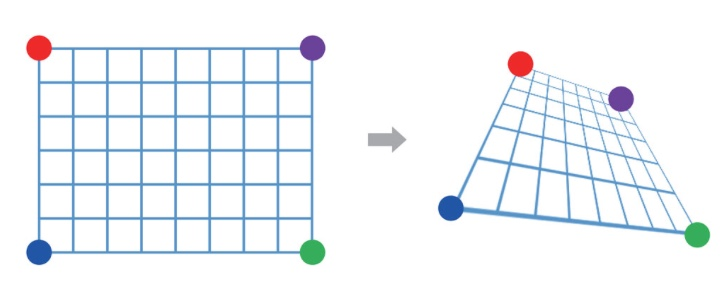
점 하나의 이동 관계로부터 x 좌표에 대한 방정식 하나와 y 좌표에 대한 방정식 하나를 얻을 수 있으므로 4개의 점으로부터 여덟 개의 방정식을 얻을 수 있습니다. 이렇게 얻은 여덟 개의 방정식으로부터 투시 변환을 표현하는 파라미터 정보를 계산할 수 있습니다.
투시 변환은 보통 3x3 크기의 실수 행렬로 표현하는데, 여덟 개의 파라미터로 표현할 수도 있지만 좌표 계산의 편의상 9개의 원소를 갖는 3x3 행렬을 사용합니다. 투시 변환을 표현하는 행렬을 \(M_P\)라고 하면, 입력 영상의 픽셀 좌표 (x, y)가 행렬 \(M_P\)에 의해 이동하는 결과 영상의 픽셀 좌표 (x', y')는 다음과 같이 계산됩니다.
\[\begin{bmatrix} wx' \\ wy' \\ w \end{bmatrix} = M_P\begin{bmatrix} x \\ y \\ 1 \end{bmatrix} = \begin{bmatrix} p_{11} & p_{12} & p_{13} \\ p_{21} & p_{22} & p_{23} \\ p_{31} & p_{32} & p_{33} \end{bmatrix}\begin{bmatrix} x \\ y \\ 1 \end{bmatrix}\]
위 행렬 수식에서 입력 좌표와 출력 좌표를 (x, y, 1), (wx', wy', w) 형태로 표현한 것을 동차 좌표계(homogeneous coordinate)라고 하며, 좌표 계산의 편의를 위해 사용하는 방식입니다. 여기서 w는 결과 영상의 좌표를 표현할 때 사용되는 비례 상수입니다. 위 식에 따라서 x'와 y'는 다음과 같이 계산할 수 있습니다.
\[\begin{matrix} x' = \frac{p_{11}x + p_{12}y + p_{13}}{p_{31}x + p_{32}y + p_{33}} & y' = \frac{p_{21}x + p_{22}y + p_{23}}{p_{31}x + p_{32}y + p_{33}} \end{matrix}\]
OpenCV는 투시 변환 행렬을 구하는 함수와 이 행렬을 이용하여 실제 영상을 투시 변환하는 함수를 모두 제공합니다. 먼저 투시 변환 행렬을 구하는 함수는 getPerspectiveTransform() 입니다.

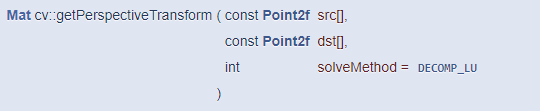
이 함수는 src에 저장된 4개의 점을 dst 좌표의 점으로 옮기는 투시 변환 행렬을 반환합니다. 점의 좌표를 담고 있는 src와 dst는 Point2f 타입의 배열을 사용해도 되고, vector<Point2f> 타입을 사용해도 됩니다. 이 함수가 반환하는 Mat 객체는 CV_64FC1 타입을 사용하는 3x3 크기의 행렬입니다.
이 행렬을 구하고 나면, warpPerspective() 함수를 통해 투시 변환을 수행할 수 있습니다.
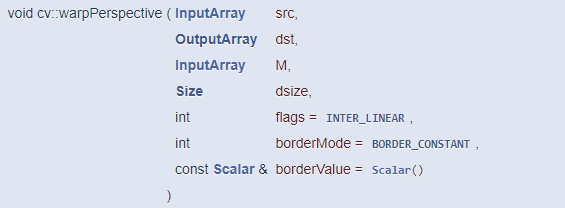

이 함수로 전달되는 투시 변환 행렬 M은 CV_32FC1 또는 CV_64FC1 타입이어야 하고, 크기는 3x3 이어야 합니다. 투시 변환 결과 영상의 크기 dsize는 사용자가 적절하게 지정해야 하고, dsize에 Size()를 지정하면 입력 영상과 같은 크기의 결과 영상을 생성합니다.
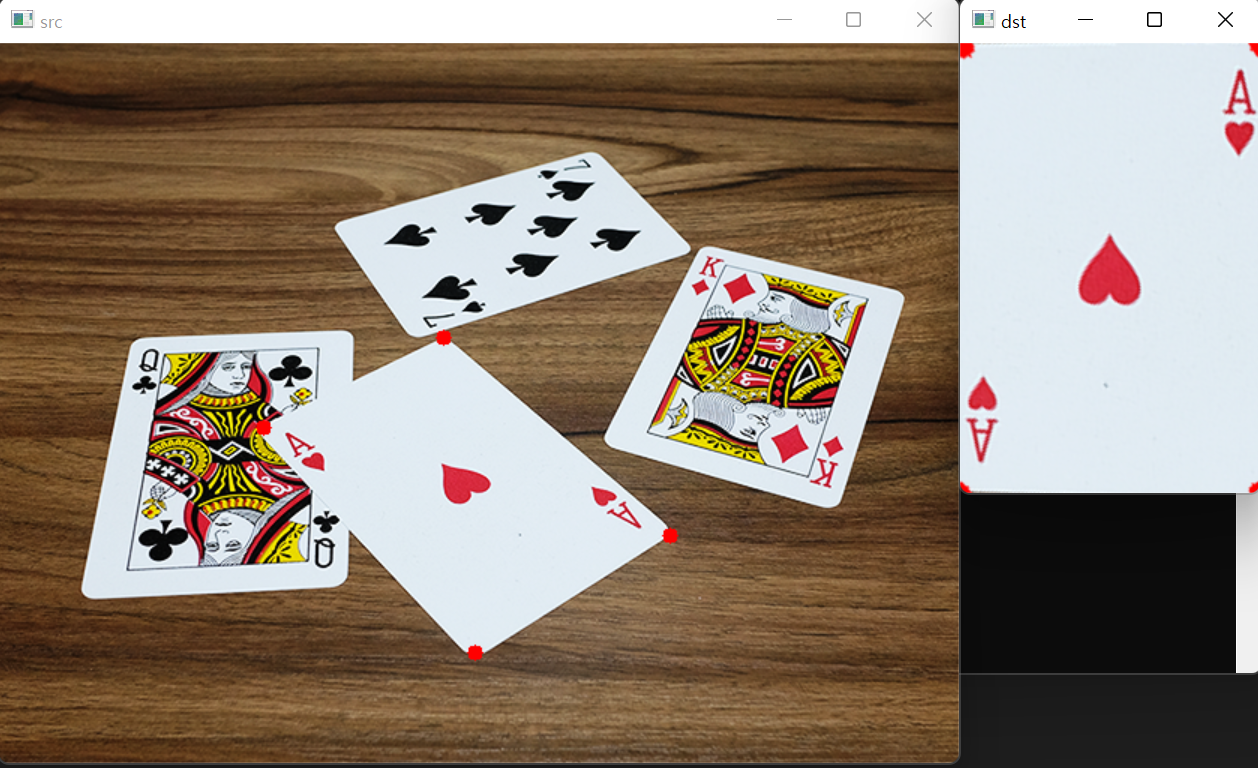
위의 두 함수를 이용하여 투시 변환 행렬을 구하고, 이를 이용하여 실제 영상을 투시 변환하는 예제 코드입니다. 이 코드는 card.bmp에서 사용자가 마우스로 카드 모서리 좌표를 선택하면 해당 카드를 반듯한 직사각형 형태로 투시 변환하여 화면에 출력합니다.
#include <iostream>
#include "opencv2/opencv.hpp"
cv::Mat src;
cv::Point2f srcQuad[4], dstQuad[4];
void on_mouse(int event, int x, int y, int flags, void* userdata)
{
static int cnt = 0;
if (event == cv::EVENT_LBUTTONDOWN) {
if (cnt < 4) {
srcQuad[cnt++] = cv::Point2f(x, y);
cv::circle(src, cv::Point(x, y), 5, cv::Scalar(0, 0, 255), -1);
cv::imshow("src", src);
if (cnt == 4) {
int w = 200, h = 300;
dstQuad[0] = cv::Point2f(0, 0);
dstQuad[1] = cv::Point2f(w - 1, 0);
dstQuad[2] = cv::Point2f(w - 1, h - 1);
dstQuad[3] = cv::Point2f(0, h - 1);
cv::Mat pers = cv::getPerspectiveTransform(srcQuad, dstQuad);
cv::Mat dst;
cv::warpPerspective(src, dst, pers, cv::Size(w, h));
cv::imshow("dst", dst);
}
}
}
}
int main(int argc, char* argv[])
{
src = cv::imread("card.bmp");
if (src.empty()) {
std::cout << "Image load failed!\n";
return -1;
}
cv::imshow("src", src);
cv::namedWindow("src");
cv::setMouseCallback("src", on_mouse);
cv::imshow("src", src);
cv::waitKey();
cv::destroyAllWindows();
}위 코드의 실행 결과는 다음과 같습니다.
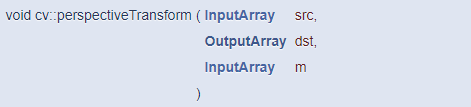
참고로 3x3 투시 변환 행렬이 있을 때, 일부 점들의 투시 변환 결과를 알고 싶다면 perspectiveTransform() 함수를 사용하면 됩니다.

'프로그래밍 > OpenCV' 카테고리의 다른 글
| [OpenCV] 컬러 이미지 처리 (0) | 2022.05.09 |
|---|---|
| [OpenCV] 에지 검출 (0) | 2022.05.08 |
| [OpenCV] 영상 필터링 (0) | 2022.05.06 |
| [OpenCV] 영상 밝기/명암비, 히스토그램 (0) | 2022.05.05 |
| [OpenCV] 이벤트 처리 (0) | 2022.05.04 |




댓글