References
- https://github.com/opencv/opencv
- https://docs.opencv.org/
- OpenCV 4로 배우는 컴퓨터 비전과 머신러닝
Contents
- 필터링(filtering) 연산
- 엠보싱 필터링
- 블러링 (평균값 필터, 가우시안 필터)
- 샤프닝 (언샤프 필터)
- 노이즈 제거 필터링
필터링 연산
영상 처리에서 필터링(filtering)은 영상에서 원하는 정보만 통과시키고 원치 않는 정보는 걸러 내는 작업입니다. 예를 들면, 노이즈를 제거하여 영상을 깔끔하게 만드는 필터가 있고, 또는 부드러운 느낌의 성분을 제거하여 날카로운 느낌이 나도록 만들 수도 있습니다.
영상의 필터링은 보통 마스크(mask)라고 부르는 작은 크기의 행렬을 이용하는데, 마스크는 필터링의 성격을 정의하는 행렬이며 커널(kernel), 윈도우(window)라고도 부릅니다. 경우에 따라서는 마스크 자체를 필터라고 부르기도 합니다. 마스크는 다양한 크기와 모양으로 정의할 수 있으며, 마스크 행렬의 원소는 보통 실수로 구성됩니다.
영상 처리에서 사용되는 필터 마스크는 위와 같이 다양합니다. 1x3, 3x1 형태 직사각형 행렬을 사용하기도 하고, 3x3, 5x5 등 정사각 행렬을 사용하기도 합니다. 필요하다면 십자가 모양의 마스크를 사용할 수도 있습니다. 다양한 필터 마스크 중에서 3x3 행렬이 가장 널리 사용됩니다. 위의 마스크에서 진한 색으로 표시된 위치는 고정점(anchor point)을 나타냅니다. 이 점은 현재 필터링 작업을 수행하고 있는 기준 픽셀 위치를 나타내고, 대부분의 경우 행렬의 정중앙을 고정점으로 사용합니다.
필터링 연산의 결과는 마스크 행렬의 모양과 원소 값에 의해 결정되는데, 마스크 행렬을 어떻게 정의하느냐에 따라 영상을 전반적으로 부드럽게 만들 수도 있고, 반대로 날카롭게 만들 수도 있습니다. 또는 영상에서 노이즈를 제거하거나 에지(edge) 성분만 나타나도록 만들 수도 있습니다.
가장 널리 사용되는 3x3 마스크를 이용한 필터링 수행 방법을 그림으로 나타내면 다음과 같습니다.
딥러닝에 대해 아신다면 위 그림이 익숙할 수 있습니다. 위 그림에서 m은 마스크, f는 입력, g는 출력입니다. 그리고 마스크 행렬 크기가 3x3이므로 고정점의 좌표를 (1,1)로 설정하였습니다. 마스크를 이용한 필터링은 입력의 모든 픽셀 위로 마스크 행렬을 이동시키면서 마스크 연산을 수행하는 방식으로 이루어지며, 마스크 연산은 마스크 행렬의 모든 원소에 대하여 마스크 행렬 원소 값과 같은 위치에 있는 입력 영상 픽셀값을 서로 곱한 후, 그 결과를 모두 더하는 것을 의미합니다. 그리고 마스크 연산의 결과는 출력 영상에서 고정점 위치에 대응되는 픽셀 값으로 설정합니다. 이 연산은 딥러닝에서의 convolution 연산과 유사합니다.
따라서, 마스크 행렬의 중심이 입력 영상의 (x, y) 좌표 위에 위치했을 때, 필터링 결과 영상의 픽셀 값 \(g(x, y)\)는 다음과 같이 계산됩니다.
\[\begin{align*} g(x, y) &= m(0,0)f(x-1,y-1) + m(1,0)f(x,y-1) + m(2,0)f(x+1,y-1) \\ &+ m(0,1)f(x-1,y) + m(1,1)f(x,y) +m(2,1)f(x+1,y) \\ &+ m(0,2)f(x-1,y+1) + m(1,2)f(x,y+1) + m(2,2)f(x+1,y+1)\end{align*}\]
(x, y) 좌표에서 마스크 연산을 통해 결과 영상의 픽셀 값 \(g(x, y)\)를 구했으면, 다음에는 마스크를 한 픽셀 옆으로 이동하여 (x+1, y) 좌표에 다시 마스크 연산을 수행하고 그 결과를 \(g(x+1, y)\)에 저장합니다. 이 과정을 전체 픽셀에 대해 수행하면 필터링이 완료됩니다.
그런데, 영상의 맨 바깥쪽 픽셀에서는 위의 수식을 그대로 적용하기 어려운데, 위 식을 (0, 1) 좌표에서 그대로 적용하면 계산을 위해서 f(-1,0), f(-1,1), f(-1,2)의 픽셀 값을 참조해야 합니다. 그런데 이 픽셀들은 실제 영상에 존재하지 않습니다. 따라서 이 수식은 적용할 수 없으며, 영상의 가장자리 픽셀에 대해서는 특별한 처리를 해주어야 합니다.
OpenCV에서는 영상의 필터링을 수행할 때, 영상의 가장자리 픽셀을 확장하여 바깥쪽에 가상의 픽셀을 만듭니다. 즉, 패딩(padding)을 추가합니다. 이때 이 가상의 픽셀 값을 어떻게 설정하느냐에 따라 필터링 연산의 결과가 달라집니다. OpenCV의 필터링 연산에서 사용할 수 있는 가장자리 픽셀 확장 방법은 BorderTypes라는 이름의 열거형 상수로 설정할 수 있는데, 설정할 수 있는 옵션은 다음과 같습니다.
OpenCV에서 필터 마스크를 사용하는 일반적인 필터링은 filter2D() 함수를 사용합니다.
이 함수는 src 영상에 kernel 필터를 이용하여 필터링을 수행하고, 그 결과를 dst에 저장합니다. 만약 src와 dst에 같은 변수를 지정하면 필터링 결과를 입력 영상에 덮어쓰게 됩니다. filter2D() 함수가 수행하는 연산을 수식으로 표현하면 다음과 같습니다.
\[\texttt{dst} (x,y) = \sum_{\substack{0 \leq x' < \texttt{kernel.cols} \\ { 0 \leq y' < \texttt{kernel.rows}}}} \texttt{kernel} (x',y')* \texttt{src} (x+x'- \texttt{anchor.x},y+y'- \texttt{anchor.y})\]
filter2D() 함수 인자 중에서 ddepth는 결과 영상의 깊이를 지정하는 용도로 사용하며, 입력 영상 깊이에 따라 지정할 수 있는 ddepth 다음과 같습니다.
anchor, delta, borderType 인자는 기본값을 가지고 있기 때문에 생략할 수 있습니다. anchor 인자는 커널 행렬에서 고정점으로 사용할 좌표이며, 기본값인 Point(-1, -1)을 지정하면 커널 행렬 중심 좌표를 고정점으로 사용합니다. delta 인자에는 필터링 연산 후 결과 영상에 추가적으로 더할 값을 지정하며, 기본값은 0입니다. borderType은 앞서 설명한 BorderTypes 열거형 상수 중 하나를 지정할 수 있습니다.
엠보싱 필터링
이번에는 filter2D() 함수를 사용하여 영상에 엠보싱(embossing) 필터링을 적용하는 코드를 작성해보겠습니다. 보통 입력 영상에서 픽셀 값 변화가 적은 평탄한 영역은 회색으로 설정하고, 객체의 경계 부분은 좀 더 밝거나 어둡게 설정하면 엠보싱 느낌이 납니다.
간단한 엠보싱 필터 마스크는 다음과 같습니다.
위 필터 마스크는 대각선 방향으로 +1 또는 -1의 값이 지정된 3x3 행렬입니다. 이 필터 마스크를 사용하여 필터링을 수행하면 대각선 방향으로 픽셀값이 급격하게 변하는 부분에서 결과 영상 픽셀 값이 0보다 훨씬 크거나 0보다 훨씬 작은 값을 가지게 됩니다. 만약 픽셀 값이 크게 바뀌지 않는 평탄한 영역에서는 결과 영상의 픽셀 값이 0에 가까운 값을 가지게 됩니다. 이렇게 구한 결과를 그대로 화면에 나타내면 음수 값은 모두 포화 연산에 의해 0이 되어 버리기 때문에 입체감이 크게 줄어들게 되는데, 보통 128을 더해서 보기 좋게 만듭니다.
아래 코드는 엠보싱 필터링을 수행하는 코드입니다.
#include <iostream>
#include "opencv2/opencv.hpp"
int main(int argc, char* argv[])
{
cv::Mat src = cv::imread("rose.bmp", cv::IMREAD_GRAYSCALE);
if (src.empty()) {
std::cout << "Image load failed!\n";
return -1;
}
float data[] = { -1, -1, 0, -1, 0, 1, 0, 1, 1 };
cv::Mat emboss(3, 3, CV_32FC1, data);
cv::Mat dst;
cv::filter2D(src, dst, -1, emboss, cv::Point(-1, -1), 128);
cv::imshow("src", src);
cv::imshow("dst", dst);
cv::waitKey();
cv::destroyAllWindows();
}위 코드에서 emboss 행렬은 위에서 살펴본 3x3 실수형 행렬입니다. 이 행렬을 filter2D() 함수에 전달하여 엠보싱 필터링을 수행했고, 그 결과는 dst에 저장됩니다. 입체감이 나타나도록 delta 인자에 128을 지정하였습니다.
실행 결과는 다음과 같습니다.
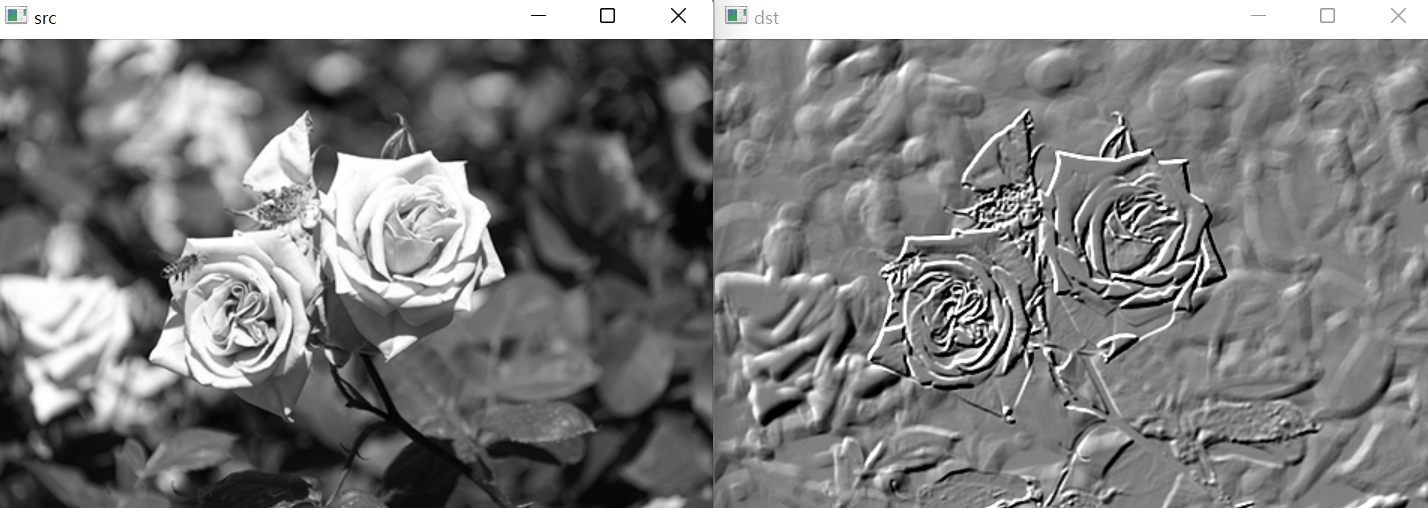
dst에서 장미꽃 경계 부분이 입체감 있게 표현된 것을 확인할 수 있습니다. 그리고 픽셀 값이 완만하게 바뀌는 부분에서는 필터링 결과 영상이 대체로 밝기 값 128에 가까운 회색으로 표현되었습니다.
블러링 (blurring)
블러링은 초점이 맞지 않는 사진처럼 영상을 부드럽게 만드는 필터링 기법이며 스무딩(smoothing)이라고 표현하기도 합니다. 인접한 픽셀 간의 픽셀 값 변화가 크지 않은 경우 부드러운 느낌을 받을 수 있습니다. 이 효과는 거친 느낌의 영상을 부드럽게 만드는 용도로 사용되기도 하고, 또는 영상에 존재하는 노이즈를 제거하는 전처리 과정으로도 사용됩니다. 여기서는 간단한 평균값 필터를 사용하는 블러링 기법과 조금 더 자연스러운 블러링을 수행하는 가우시안 필터에 대해 살펴보겠습니다.
평균값 필터
평균값 필터(mean filter)는 입력 영상에서 특정 픽셀과 주변 픽셀들의 산술 평균을 결과 영상 픽셀 값으로 설정하는 필터입니다. 평균값 필터에 의해 생성되는 결과는 급격한 변화들이 감소되어 날카로운 에지들이 무뎌지고 노이즈의 영향이 크게 사라지는 효과가 있습니다. 다만 너무 과도하게 사용하면 사물의 경계가 흐릿해지고 사물의 구분이 어려워질 수 있습니다.
3x3과 5x5 크기의 평균값 필터 마스크는 다음과 같습니다.
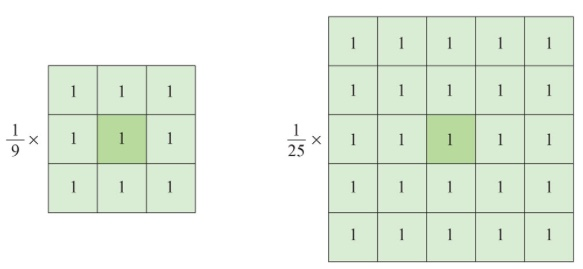
각각의 행렬은 모두 원소 값이 1로 설정되어 있고, 행렬의 전체 원소 개수로 각 행렬 원소 값을 나누는 형태로 표현됩니다. 결국 3x3 평균값 필터는 모든 원소가 1/9로 설정되고, 5x5는 1/25로 설정됩니다. 평균값 필터는 마스크의 크기가 커지면 커질수록 더욱 부드러운 느낌의 결과를 생성하지만, 연산량이 크게 증가할 수 있습니다.
OpenCV에서는 blur() 함수를 이용하여 평균값 필터링을 수행할 수 있습니다.
blur() 함수는 src 영상에 ksize 크기의 평균값 필터 마스크를 사용하여 dst 출력 영상을 생성합니다. anchor 인자와 borderType 인자는 기본값을 가지고 있으므로 생략 가능하며, blur() 함수에서 사용하는 커널은 다음과 같습니다.
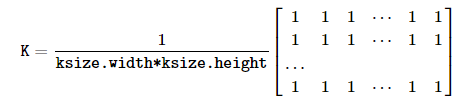
blur() 함수를 사용하여 실제 이미지에 블러링을 수행하는 코드는 다음과 같습니다.
#include <iostream>
#include "opencv2/opencv.hpp"
int main(int argc, char* argv[])
{
cv::Mat src = cv::imread("rose.bmp", cv::IMREAD_GRAYSCALE);
if (src.empty()) {
std::cout << "Image load failed!\n";
return -1;
}
cv::Mat dst;
for (int ksize = 3; ksize <= 7; ksize += 2) {
cv::blur(src, dst, cv::Size(ksize, ksize));
cv::String desc = cv::format("Mean: %dx%d", ksize, ksize);
cv::putText(dst, desc, cv::Point(10, 30), cv::FONT_HERSHEY_SIMPLEX, 1.0, cv::Scalar(255), 1, cv::LINE_AA);
cv::imshow("dst", dst);
cv::waitKey();
}
cv::destroyAllWindows();
}위 함수의 실행 결과는 다음과 같습니다.
평균값 필터의 크기가 커질수록 결과 이미지가 더욱 부드럽게 변경되는 것을 확인할 수 있습니다.
가우시안 필터
가우시안 필터는 가우시안 분포(gaussian distribution) 함수를 근사하여 생성한 필터 마스크를 사용하는 기법입니다.
가우시안 분포는 평균을 중심으로 좌우 대칭의 종 모양을 갖는 확률 분포를 말하며 정규 분포(normal distribution)라고도 합니다. 가우시안 분포는 평균과 표준 편차에 따라 분포 모양이 결정되는데, 영상에서 사용되는 가우시안 분포는 주로 평균이 0인 가우시안 분포를 사용합니다. 평균이 0이고 표준 편차가 \(\sigma\)인 1차원 가우시안 분포를 함수로 표현하면 다음과 같습니다.
\[G_\sigma (x) = \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{x^2}{2\sigma^2}}\]
평균이 0이고 표준 편차가 각각 0.5, 1.0, 2.0인 가우시안 분포 그래프는 다음과 같습니다. 가우시안 분포 함수 값은 특정 x가 발생할 수 있는 확률의 개념을 가지며, 그래프 아래 면적을 모두 더하면 1이 됩니다.
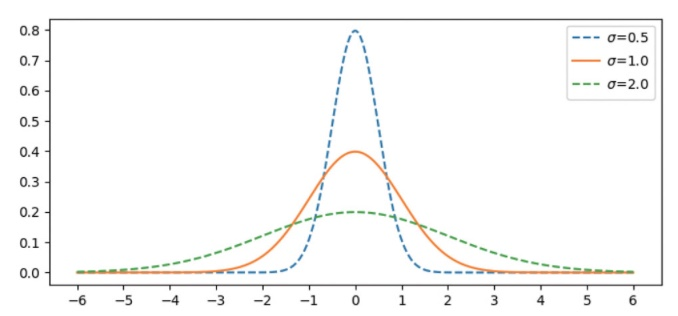
가우시안 분포를 따르는 2차원 필터 마스크 행렬을 생성하려면 2차원 가우시안 분포 함수를 근사해야 합니다. 2차원 가우시안 분포 함수는 x와 y 두 개의 변수를 사용하고, 분포의 모양을 결정하는 평균과 표준 편차도 x축, y축에 따라 따로 설정합니다. 평균이 (0, 0)이고 표준 편차가 각각 \(\sigma_x, \sigma_y\)인 2차원 가우시안 분포 함수는 다음과 같이 정의됩니다.
\[G_{\sigma_x, \sigma_y}(x, y) = \frac{1}{2\pi \sigma_x \sigma_y}e^{-(\frac{x^2}{2\sigma_x ^2} + \frac{y^2}{2\sigma_y ^2})}\]
평균이 (0, 0)이고 표준 편차가 각각 1.0인 2차원 가우시안 분포 함수 그래프는 다음과 같습니다.
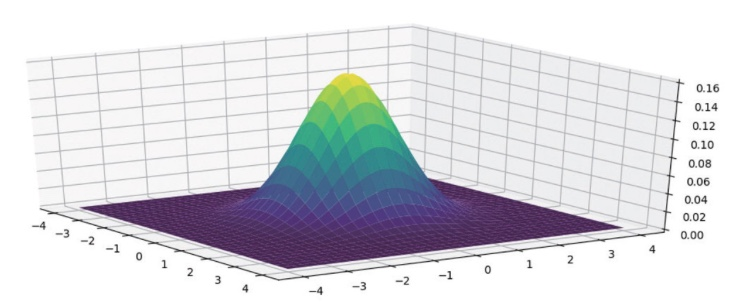
2차원 가우시안 함수 분포 그래프 또한 함수 그래프 아래의 부피를 구하면 1이 됩니다.
가우시안 필터는 이러한 2차원 가우시안 분포 함수로부터 구한 마스크 행렬을 사용합니다. 가우시안 분포 함수는 연속 함수이지만 이산형의 마스크를 만들기 위해서 x와 y값이 정수인 위치에서만 가우시안 분포 함수 값을 추출하여 마스크를 생성합니다. 평균이 0이고 표준 편차가 \(\sigma\)인 가우시안 분포는 x가 \(-4\sigma\)부터 \(4\sigma\) 사이인 구간에서 그 값의 대부분이 존재하기 때문에 가우시안 필터 마스크의 크기는 보통 \(8\sigma + 1\)로 결정합니다. 예를 들어, 각 표준 편차가 1.0인 가우시안 함수를 사용하는 경우, x = {-4, -3, -2, -1, 0, 1, 2, 3, 4}, y = {-4, -3, -2, -1, 0, 1, 2, 3, 4}인 경우에만 가우시안 함수 값을 추출하여 필터 마스크를 생성합니다.
OpenCV에서 가우시안 필터링을 수행하려면 GaussianBlur() 함수를 사용합니다.
이 함수는 src에 가우시안 필터링을 수행하고 dst에 저장합니다. x축과 y축의 표준 편차인 sigmaX와 sigmaY는 서로 다른 값을 지정해도 되지만, 특별한 이유가 있는게 아니라면 보통 같은 값을 사용합니다. sigmaY에 인자를 지정하지 않거나 0을 지정하면 sigmaX와 같은 표준 편차를 사용합니다. 또한 가우시안 필터의 크기를 결정하는 ksize 인자에도 특별한 이유가 없다면 cv::Size()를 전달하여 적절한 필터 크기를 자동으로 결정하도록 하는 것이 좋습니다.
GaussianBlur() 함수를 사용하여 실제 영상에 가우시안 필터를 적용하는 코드는 다음과 같습니다.
#include <iostream>
#include "opencv2/opencv.hpp"
int main(int argc, char* argv[])
{
cv::Mat src = cv::imread("rose.bmp", cv::IMREAD_GRAYSCALE);
if (src.empty()) {
std::cout << "Image load failed!\n";
return -1;
}
cv::imshow("src", src);
cv::Mat dst;
for (int sigma = 1; sigma <= 5; sigma++) {
cv::GaussianBlur(src, dst, cv::Size(), (double)sigma);
cv::String text = cv::format("sigma = %d", sigma);
cv::putText(dst, text, cv::Point(10, 30), cv::FONT_HERSHEY_SIMPLEX, 1.0, cv::Scalar(255), 1, cv::LINE_AA);
cv::imshow("dst", dst);
cv::waitKey();
}
cv::destroyAllWindows();
}위 코드 실행 결과는 다음과 같습니다.
표준 편차의 값이 커질수록 결과 이미지가 더욱 부드럽게 변경되는 것을 확인할 수 있습니다.
샤프닝
이번에는 블러링과 반대되는 개념인 샤프닝(sharpening) 기법에 대해 알아보겠습니다. 샤프닝은 초점이 잘 맞은 사진처럼 윤곽이 뚜렷하고 선명한 느낌이 나도록 영상을 변경하는 기법입니다.
언샤프 마스크 필터
샤프닝을 구현하기 위해서는 블러링된 이미지를 사용합니다. 즉, 블러링이 적용되어 부드러워진 영상을 활용하여 반대로 날카로운 영상을 생성합니다. 여기서 블러링이 적용된 영상을 언샤프하다고 말하기도 합니다. 이처럼 언샤프한 영상을 이용하여 역으로 날카로운 영상을 생성하는 필터를 언샤프 마스크 필터(unsharp mask filter)라고 합니다.
언샤프 마스크 필터링의 과정은 다음과 같습니다.
먼저 원본 영상 \(f(x, y)\)에 블러링을 적용한 결과 \(\bar{f}(x, y)\)를 구합니다. 그리고 입력 \(f(x, y)\)에서 블러링된 결과 \(\bar{y}(x, y)\)를 뺀 \(g(x, y)\)를 구합니다. 즉, \(g(x, y) = f(x, y) - \bar{f}(x, y)\)입니다. 이렇게 계산한 \(g(x, y)\)를 다시 입력 \(f(x, y)\)에 더하면 에지가 강조된 \(h(x, y)\) 함수가 생성됩니다. 즉, \(h(x, y)\)가 샤프닝이 적용된 결과가 됩니다.
\[h(x, y) = f(x, y) + g(x, y)\]
\(g(x, y)\)는 입력 영상에서 블러링된 영상을 뺀 결과이므로 입력 영상에서 오직 날카로운 성분만 가지고 있는 함수라고 할 수 있습니다. 따라서 입력 \(f(x, y)\)에 \(g(x, y)\)를 더함으로써 날카로운 성분이 강조된 최종 영상 \(h(x, y)\)가 얻어지는 것으로 해석할 수 있습니다. 그런데 \(f(x, y)\)에 \(g(x, y)\)를 단순하게 더하는 것이 아니라 실수 가중치를 곱한 후 더하면 날카로운 정도를 조절할 수 있씁니다. 즉, 샤프닝이 적용된 결과 영상 \(h(x, y)\)의 수식을 다음과 같이 수정할 수 있습니다.
\[h(x, y) = f(x, y) + \alpha g(x, y)\]
위 수식에서 \(\alpha\)는 날카로운 정도를 조절할 수 있는 파라미터이며, 1.0을 지정하면 날카로운 성분을 그대로 한 번 더하는 셈이고, 1보다 작은 값을 지정하면 조금 덜 날카로운 영상을 만들 수 있습니다. 위 수식에서 \(g(x, y)\) 대신 \(f(x, y) - \bar{f}(x, y)\)를 대입하고 식을 정리하면 다음과 같습니다.
\[\begin{align*} h(x, y) &= f(x, y) + \alpha(f(x, y) - \bar{f}(x, y)) \\ &= (1 + \alpha)f(x, y) - \alpha\bar{f}(x, y) \end{align*}\]
OpenCV에서 언샤프 마스크 필터 함수는 따로 제공하지는 않지만, 위 수식을 이용하면 쉽게 구현할 수 있습니다. 샤프닝을 적용하는 코드는 다음과 같습니다. 여기서 \(\alpha\)는 1.0으로 고정시켜 사용하였습니다.
#include <iostream>
#include "opencv2/opencv.hpp"
int main(int argc, char* argv[])
{
cv::Mat src = cv::imread("rose.bmp", cv::IMREAD_GRAYSCALE);
if (src.empty()) {
std::cout << "Image load failed!\n";
return -1;
}
cv::imshow("src", src);
cv::Mat dst;
for (int sigma = 1; sigma <= 5; sigma++) {
cv::Mat blurred;
cv::GaussianBlur(src, blurred, cv::Size(), (double)sigma);
float alpha = 1.f;
cv::Mat dst = (1 + alpha) * src - alpha * blurred;
cv::String text = cv::format("sigma = %d", sigma);
cv::putText(dst, text, cv::Point(10, 30), cv::FONT_HERSHEY_SIMPLEX, 1.0, cv::Scalar(255), 1, cv::LINE_AA);
cv::imshow("dst", dst);
cv::waitKey();
}
cv::destroyAllWindows();
}위 코드의 실행 결과는 다음과 같습니다.
노이즈 제거 필터링
영상을 얻는 과정에서 원치 않은 잡음이 포함될 수 있습니다. 따라서 많은 컴퓨터 비전 시스템이 전처리 과정으로 노이즈를 제거하는 필터를 사용합니다.
노이즈 모델
신호 처리 관점에서 노이즈는 원본 신호에 추가된 원치 않은 신호를 의미합니다. 영상에서의 잡음은 주로 영상을 얻는 과정에서 발생하며, 디지털 카메라에서 사진을 촬영하는 경우에는 광학적 신호를 전기적 신호로 변환하는 센서에서 주로 노이즈가 추가됩니다.
카메라에서 원본 렌즈가 바라보는 장면을 원본 신호 \(s(x, y)\)라고 하고, 여기서 추가되는 노이즈를 \(n(x, y)\)라고 한다면 실제로 카메라에서 얻는 영상 신호 \(f(x, y)\)는 다음과 같이 표현합니다.
\[f(x, y) = s(x, y) + n(x, y)\]
노이즈가 생성되는 방식을 노이즈 모델(noise model)이라고 하며, 다양한 노이즈 모델 중에서 가장 대표적인 것은 가우시안 노이즈 모델(gaussian noise model)입니다. 이 모델은 보통 평균이 0인 가우시안 분포를 따르는 노이즈를 의미합니다.
평균이 0이고 표준 편차가 \(\sigma\)인 가우시안 분포는 x 값이 \(-\sigma \leq x \leq \sigma\) 구간에서 전체 데이터의 67%가 존재하고, (-2\sigma \leq x \leq 2\sigma\) 구간에는 95%, (-3\sigma \leq x \leq 3\sigma\) 구간에는 99.7%가 존재합니다. 그러므로 평균이 0이고, 표준 편차가 10인 가우시안 분포를 따르는 노이즈 모델은 67%의 확률로 -10에서 10사이의 값이 노이즈로 추가됩니다. 노이즈 값이 -20에서 20사이일 확률은 95%이며, 그 밖의 값이 노이즈로 추가될 확률은 5%입니다. 따라서 표준 편차가 작은 가우시안 노이즈 모델일수록 노이즈에 의한 픽셀 값 변화가 적다고 볼 수 있습니다.
OpenCV를 이용하면 영상에 가우시안 모델을 따르는 노이즈를 인위적으로 추가할 수 있습니다. randn() 함수는 가우시안 노이즈로 구성된 행렬을 생성하여 반환합니다.
randn() 함수는 dst 행렬을 가우시안 분포를 따르는 난수로 채웁니다. 이때 사용하는 가우시안 분포의 평균은 mean이고 표준 편차는 stddev입니다. randn() 함수에 전달되는 dst는 미리 적절한 타입으로 생성되어 있어야 하며, randn() 함수에 의해 생성된 난수는 dst 행렬의 자료형에 맞게끔 포화 연산이 수행됩니다. 평균이 0인 가우시안 노이즈를 생성할 경우 양수와 음수가 섞여 있는 난수가 발생하므로 CV_32S, CV_32F처럼 부호 있는 자료형을 사용해야 합니다.
다양한 표준 편차의 가우시안 노이즈를 영상에 추가하는 예제 코드는 다음과 같습니다. 아래 코드에서는 평균이 0이고 표준 편차가 10, 20, 30인 가우시안 노이즈를 추가하여 화면에 출력합니다.
#include <iostream>
#include "opencv2/opencv.hpp"
int main(int argc, char* argv[])
{
cv::Mat src = cv::imread("rose.bmp", cv::IMREAD_GRAYSCALE);
if (src.empty()) {
std::cout << "Image load failed!\n";
return -1;
}
cv::imshow("src", src);
cv::Mat dst;
for (int stddev = 10; stddev <= 30; stddev += 10) {
cv::Mat noise(src.size(), CV_32SC1);
cv::randn(noise, 0, stddev);
cv::Mat dst;
cv::add(src, noise, dst, cv::Mat(), CV_8U);
cv::String text = cv::format("stddev = %d", stddev);
cv::putText(dst, text, cv::Point(10, 30), cv::FONT_HERSHEY_SIMPLEX, 1.0, cv::Scalar(255), 1, cv::LINE_AA);
cv::imshow("dst", dst);
cv::waitKey();
}
cv::destroyAllWindows();
}실행 결과는 다음과 같습니다.
양방향 필터
대부분의 영상에는 가우시안 노이즈가 포함되어 있으며 많은 컴퓨터 비전 시스템이 가우시안 노이즈를 제거하기 위해 가우시안 필터를 사용합니다. 입력에서 픽셀 값이 크게 변하지 않는 평탄한 영역에 가우시안 필터가 적용되는 경우, 주변 픽셀 값이 부드럽게 블러링되면서 노이즈의 영향도 크게 줄어듭니다. 하지만 픽셀 값이 급격하게 변경되는 에지 근방에 동일한 가우시안 필터가 적용되면 노이즈뿐만 아니라 에지 성분까지 함께 감소하게 됩니다. 즉, 노이즈가 감소하면서 함께 에지도 무뎌지기 때문에 객체의 윤곽이 흐릿해질 수 있습니다.
이러한 단점을 보완하기 위해 에지 정보는 그대로 유지하면서 노이즈만 제거하는 에지 보전 노이즈 제거 필터(edge-preserving noise removal filter)에 대해 연구했는데, 이중에 1998년 제안된 양방향 필터(bilateral filter)는 에지 성분을 그대로 유지하면서 가우시안 노이즈를 효과적으로 제거하는 알고리즘입니다.
양방향 필터는 아래의 공식을 사용하여 필터링을 수행합니다.
\[g_\textbf{\textsf{p}} = \frac{1}{W_\textbf{\textsf{p}}}\sum_{\textbf{\textsf{q}} \in S}G_{\sigma_S}(\left \| \textbf{\textsf{p}} - \textbf{\textsf{q}} \right \|)G_{\sigma_\Gamma}(f_{\textbf{\textsf{p}}} - f_{\textbf{\textsf{q}}})f_{\textbf{\textsf{q}}}\]
위 수식에서 f는 입력 영상, g는 출력 영상, 그리고 \(\textbf{\textsf{{p}}}\)와 \(\textbf{\textsf{{q}}}\)는 픽셀의 좌표를 나타냅니다. \(f_p\)와 \(f_q\)는 각 점에서의 입력 영상 픽셀 값이고, \(g_p\)는 \(\textbf{\textsf{{p}}}\)점에서의 출력 영상 픽셀 값입니다. \(G_{\sigma_S}\)와 \(G_{\sigma_\Gamma}\)는 각각 표준 편차가 \(\sigma_S\), \(\sigma_\Gamma\)인 가우시안 분포 함수입니다. S는 필터 크기를 나타내고 \(W_p\)는 양방향 필터 마스크 합이 1이 되도록 만드는 정규화 상수입니다. 양방향 필터 수식은 매우 복잡해 보이지만 자세히 살펴보면 두 개의 가우시안 함수의 곱으로 구성된 필터입니다.
먼저 \(G_{\sigma_S}(\left \| \textbf{\textsf{p}} - \textbf{\textsf{q}} \right \|)\) 함수는 두 점 사이의 거리에 대한 가우시안 함수로, 위에서 설명한 가우시안 필터와 완전히 같은 의미로 동작합니다. 반면, \(G_{\sigma_\Gamma}(f_{\textbf{\textsf{p}}} - f_{\textbf{\textsf{q}}})\) 함수는 두 점의 픽셀 값 차이에 의한 가우시안 함수입니다. 이 함수는 두 점의 픽셀 밝기 값의 차이가 적은 평탄한 영역에서는 큰 가중치를 갖게 만들고, 반면에 에지를 사이에 두고 있는 픽셀에 대해서는 거의 0에 가까운 값이 됩니다. 이로 인해 에지 근방에서는 가우시안 블러링 효과가 거의 나타나지 않고 에지가 보존됩니다.
양방향 필터 수식이 필터 값의 차이에 의존적이기 때문에 양방향 필터 마스크는 영상의 모든 픽셀에서 서로 다른 형태를 갖게 됩니다. 즉, 모든 픽셀 위치에서 주변 픽셀과의 밝기 차이에 의한 고유의 필터 마스크 행렬을 만들어서 마스크 연산을 수행해야 합니다. 이는 일반적인 가우시안 블러링이 모든 위치에서 일정한 가우시안 마스크 행렬을 사용하는 것과 차이가 있으며, 따라서 가우시안 블러링보다 훨씬 많은 연산량이 필요합니다.
OpenCV에서는 bilateralFilter() 함수를 이용하여 양방향 필터를 적용할 수 있습니다.
이 함수에서 sigmaSpace 값은 일반적인 가우시안 필터링에서 사용하는 표준 편차와 같습니다. 즉, 값이 클수록 더 많은 주변 픽셀을 고려하여 블러링을 수행합니다. sigmaColor 값은 주변 픽셀과의 밝기 차이에 관한 표준 편차이며, 값이 작게 지정할 경우, 픽셀 값 차이가 큰 주변 픽셀과는 블러링이 적용되지 않습니다. 반면 sigmaColor를 크게 지정하면 픽셀 값 차이가 조금 크더라도 블러링이 적용됩니다. 즉, sigmaColor 값을 이용하여 어느 정도 밝기 차를 갖는 에지를 보존할 것인지를 결정할 수 있습니다.
가우시안 노이즈가 추가된 이미지에 양방향 필터를 적용하는 코드는 다음과 같습니다. 위의 가우시안 필터 코드에서처럼 이미지에 가우시안 노이즈를 추가하고, 가우시안 블러와 양방향 필터를 각각 적용하여 결과를 비교합니다.
#include <iostream>
#include "opencv2/opencv.hpp"
int main(int argc, char* argv[])
{
cv::Mat src = cv::imread("rose.bmp", cv::IMREAD_GRAYSCALE);
if (src.empty()) {
std::cout << "Image load failed!\n";
return -1;
}
cv::Mat noise(src.size(), CV_32SC1);
cv::randn(noise, 0, 10);
cv::add(src, noise, src, cv::Mat(), CV_8U);
cv::Mat dst1;
cv::GaussianBlur(src, dst1, cv::Size(), 5);
cv::Mat dst2;
cv::bilateralFilter(src, dst2, -1, 10, 5);
cv::imshow("src", src);
cv::imshow("dst1", dst1);
cv::imshow("dst2", dst2);
cv::waitKey();
cv::destroyAllWindows();
}실행 결과는 다음과 같습니다.
미디언 필터
미디언 필터(midian filter)는 입력 영상에서 자기 자신 픽셀과 주변 픽셀 값 중에서 중간값을 선택하여 결과 영상의 픽셀 값으로 설정하는 기법입니다. 이 필터는 입력의 픽셀 값과 마스커 행렬을 서로 곱한 후 모두 더하는 형태의 연산을 사용하지 않으며, 주변 픽셀 값들의 중간값을 선택하기 위해 내부에서 픽셀 값 정렬 과정이 사용됩니다. 이 필터는 특히 노이즈 픽셀 값이 주변 픽셀 값과 큰 차이가 있는 경우에 효과적으로 동작합니다.
영상에서 추가되는 노이즈 중, salt & pepper 노이즈는 픽셀 값이 일정 확률로 0 또는 255로 변경되는 형태의 노이즈입니다. 이 노이즈가 추가된 영상에 미디언 필터를 적용하면 대부분 salt & pepper 노이즈가 아닌 원본 영상에 존재하는 픽셀 값이 중간값으로 선택되기 때문에 효과적으로 노이즈가 제거됩니다.
OpenCV에서는 medianBlur() 함수를 이용하여 미디언 필터링을 적용할 수 있습니다.
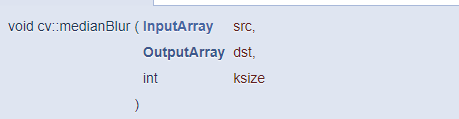
이 함수는 ksize x ksize 크기의 필터를 이용하여 필터링을 수행합니다. 다채널 영상인 경우 각 채널별로 필터링을 수행합니다. 이 함수는 내부적으로 BORDER_REPLICATE 방식을 사용하여 가장자리 픽셀 값을 설정하여 필터링을 수행합니다.
이 함수를 사용하여 미디언 필터링을 수행하는 예제 코드는 다음과 같습니다. 이 코드에서는 입력 전체 크기의 10%에 해당하는 픽셀에 salt & pepper 노이즈를 추가하고, 가우시안 필터와 미디언 필터를 수행한 결과 영상을 화면에 출력합니다.
#include <iostream>
#include "opencv2/opencv.hpp"
int main(int argc, char* argv[])
{
cv::Mat src = cv::imread("rose.bmp", cv::IMREAD_GRAYSCALE);
if (src.empty()) {
std::cout << "Image load failed!\n";
return -1;
}
int num = (int)(src.total() * 0.1);
for (int i = 0; i < num; i++) {
int x = rand() % src.cols;
int y = rand() % src.rows;
src.at<uchar>(y, x) = (i % 2) * 255;
}
cv::Mat dst1;
cv::GaussianBlur(src, dst1, cv::Size(), 1);
cv::Mat dst2;
cv::medianBlur(src, dst2, 3);
cv::imshow("src", src);
cv::imshow("dst1", dst1);
cv::imshow("dst2", dst2);
cv::waitKey();
cv::destroyAllWindows();
}위 코드를 실행한 결과는 다음과 같습니다.
'프로그래밍 > OpenCV' 카테고리의 다른 글
| [OpenCV] 에지 검출 (0) | 2022.05.08 |
|---|---|
| [OpenCV] 어파인 변환 / 투시 변환 (0) | 2022.05.07 |
| [OpenCV] 영상 밝기/명암비, 히스토그램 (0) | 2022.05.05 |
| [OpenCV] 이벤트 처리 (0) | 2022.05.04 |
| [OpenCV] 직선, 도형, 문자 그리기 (0) | 2022.05.04 |
댓글