[C++] 난수(random number) - random 라이브러리

References

Professional C++
https://en.cppreference.com/w/

C-스타일 난수 생성
Random Number Engines
Random Number Engine Adapters
Predefined Engines and Engine Adapters
난수 생성 예제

C++의 난수 생성 라이브러리는 다양한 알고리즘과 분포들을 사용하여 난수를 생성할 수 있습니다. 이 라이브러리는 <random> 헤더 파일에 정의되어 있으며, std 네임스페이스에 속합니다. 여기에는 크게 3개의 컴포넌트가 존재합니다: engines, engine adapters, distributions. 난수 엔진(engine)은 실제 난수를 생성하고 다음 난수를 생성하기 위한 상태를 저장합니다. 분포(distribution)은 생성되는 난수의 범위를 결정하고 이 범위 내에서 수학적으로 어떻게 분포할 지에 대해 결정합니다. 난수 엔진 어댑터는 어댑터와 관련된 난수 엔진의 결과를 수정합니다.

우선 C++의 난수 생성 라이브러리에 대해 알아보기전에 먼저 예전의 C-스타일의 난수 생성 메커니즘과 그 문제점을 간략하게 살펴보겠습니다.

C-Style Random Number Generation

C++11 이전에는 C 스타일의 함수인 srand()와 rand() 만으로 난수를 생성할 수 밖에 없었습니다. 어플리케이션에서 srand() 함수를 한 번 호출한 뒤 난수 생성기를 시드(seed)로 초기화해야 했습니다. 이를 seeding(시딩)이라고 부릅니다. 시드값은 주로 현재 시스템 시간을 사용했습니다.

소프트웨어로 난수를 생성하려면 시드값을 잘 정해야 합니다. 난수 생성기를 초기화할 때마다 같은 시드를 사용한다면 매번 동일한 난수가 생성됩니다. 그래서 현재 시스템 시간을 시드값으로 많이 사용합니다.

난수 생성기를 초기화했다면 rand() 함수로 난수를 생성할 수 있습니다. 다음 코드는 srand()와 rand()를 사용하는 방법을 보여줍니다. 여기서 time(nullptr)은 현재 시스템 시간을 리턴하며, 이 함수는 <ctime> 헤더 파일에 정의되어 있습니다.

int main()
{
    srand(static_cast<unsigned int>(time(nullptr)));
    std::cout << rand() << std::endl;
}

일정 범위 내에서 난수를 생성하려면 다음과 같이 작성합니다.

int getRandom(int min, int max)
{
    return static_cast<int>(rand() % (max + 1UL - min)) + min;
}

기존 C 스타일 rand() 함수는 0과 RAND_MAX 사이의 난수를 생성합니다. RAND_MAX는 표준에서 최소 32767 이상이라고 정의되어 있습니다. 예를 들어 GCC에서 RAND_MAX의 값은 2,147,483,647이며, 이는 signed integer의 최대값이랑 같습니다. 이러한 이유 때문에 getRandom() 함수 내에서 unsigned long 값인 1UL을 사용하여 오버플로우를 방지합니다.

아쉽게도 rand()의 낮은 자리 비트의 무작위성은 그리 높지 않습니다. 다시 말해 앞서 정의한 getRandom() 함수로 1붇터 6 사이와 같은 좁은 범위에서 난수를 생성하면 결과가 완전히 무작위로 나오지는 않습니다.

소프트웨어 기반 난수 생성기는 진정한 의미의 난수를 생성할 수 없습니다. 그래서 의사(pseudo) 난수 생성기라고도 부릅니다. 무작위인 것처럼 보이게 만드는 수학 공식에 따라 생성하기 때문입니다.

기존의 srand()와 rand() 함수는 유연성이 조금 떨어집니다. 예를 들어 난수의 분포를 변경할 수가 없습니다. 결론적으로는 srand()와 rand()를 사용하지 않는 것을 권장하고 C++의 <random> 라이브러리에서 제공되는 것들을 사용하는 것이 좋습니다.

Random Number Engines

C++의 난수 라이브러리에서 먼저 살펴볼 컴포넌트는 난수 엔진(random number engine)입니다. 이 컴포넌트는 실제 난수를 생성하는 역할을 합니다.

<random>에서는 다음과 같은 난수 엔진을 제공합니다.

random_device 엔진은 소트프웨어 기반의 생성기가 아닙니다. 컴퓨터에 특수한 하드웨어가 장착되어 있어야 사용할 수 있는 진정한 비결정적(non-deterministic) 난수 생성기입니다. 예를 들어 일정한 시간 간격 동안 발생한 알파 입자의 수를 세는 방사성 동위 원소의 자연 붕괴 속도 측정 기법이 있습니다. 컴퓨터에서 방사능이 누출될까봐 꺼림직하다면 역바이어스 다이오드(reverse-biased diode)에서 발생하는 '노이즈'를 측정하는 방식처럼 다른 물리 법칙 기반의 난수 생성기를 사용해도 됩니다. 이러한 기법에 대한 내용을 다루지는 않겠습니다.

random_device의 스펙을 보면 현재 사용하는 컴퓨터에 특수 하드웨어가 없을 때는 소프트웨어 알고리즘 중 아무거나 적용하도록 정의되어 있습니다. 어떤 알고리즘을 적용할지는 라이브러리 디자이너가 결정합니다.

난수 생성기의 성능은 엔트로피(entropy, 무질서도)로 측정합니다. random_device 클래스에서 제공하는 entropy() 메소드는 소프트웨어 기반의 의사 난수 생성기를 사용할 때는 0.0을 리턴하고, 하드웨어 장치를 사용할 때는 0이 아닌 값을 리턴합니다. 이때 리턴하는 0이 아닌 값은 장착된 디바이스의 엔트로피에 대한 측정치로 결정됩니다.

random_device 엔진의 사용법은 다소 간단합니다.

#include <iostream>
#include <random>

int main()
{
    std::random_device rnd;
    std::cout << "Entropy: " << rnd.entropy() << std::endl;
    std::cout << "Min value: " << rnd.min()
        << ", Max value: " << rnd.max() << std::endl;
    std::cout << "Random number: " << rnd() << std::endl;
}

제 PC에서 실행한 결과는 다음과 같습니다.

random_device는 대체로 의사 난수 생성 엔진보다 느립니다. 그래서 생성해야 할 난수가 아주 많다면 의사 난수 생성 엔진을 사용하고, random_device는 이 엔진의 시드를 생성하는 데만 사용하는 것이 좋습니다.

<ramdom>은 random_device 외에도 다음의 3가지 의사 난수 생성 엔진을 제공합니다.

Linear_congruential_engine(선형 합동 난수 엔진): 이 엔진은 상태 저장을 위한 메모리 사용량이 가장 적습니다. 여기서는 상태를 최종 생성된 난수를 포함한 정수 또는 아직 난수를 생성한 적이없다면 초기 시드값을 담은 정수 하나로 표현됩니다. 이 엔진의 주기는 알고리즘에 대한 매개변수에 따라 다르며 최대 \(2^64\)까지 지정할 수 있지만 대체로 그보다 적은 수로 설정합니다. 이러한 이유로 선형 합동 난수 엔진은 난수의 품질이 아주 높아야할 때는 사용하지 않는 것이 좋습니다.
mersenne_twister_engine(메르센 트위스터 난수 엔진): 소프트웨어 기반 난수 생성기 중에서 가장 품질이 좋습니다. 이 엔진의 주기는 알고리즘 매개변수에 따라 달라지지만 linear_congruential_engine보다 훨씬 깁니다. 상태 저장에 필요한 메모리 사용량도 이 매개변수에 따라 결정되지만 정수 하나로 표현하는 linear_congruential_engine보다 훨씬 큽니다. 예를 들어 기본 정의된 mersenne_twister_engine mt19937의 주기는 \(2^{19937) - 1\)이고, 상태를 2.5kBytes 가량 차지하는 625개의 정수로 표현됩니다. 이 엔진도 속도가 빠른 엔진 중의 하나입니다.
subtract_with_carry_engine(감산 캐리 난수 엔진): 상태를 100bytes 가량의 메모리에 저장하지만 난수의 생성 속도와 품질은 mersenne_twister_engine보다 떨어집니다.

random_device 엔진을 사용하는 방법은 간단하며 매개변수를 지정할 필요도 없습니다. 하지만 앞서 소개한 3가지 엔진 중 하나에 대한 인스턴스를 생성하려면 수학 매개변수를 지정해야 하는데, 이 값을 정하는 방법은 쉽지 않습니다. 어떤 매개변수를 지정하느냐에 따라 생성된 난수의 품질이 크게 달라집니다.

예를 들어 mersenne_twister_engine 클래스는 매개변수를 다음과 같이 정의하고 있습니다.

template<class UIntType, size_t w, size_t n, size_t m, size_t r,
    UIntType a, size_t u, UIntType d, size_t s,
    UIntType b, size_t t, UIntType c, size_t l, UIntType f>
class mersenne_twister_engine {...}

매개변수가 무려 14개나 됩니다. linear_congruential_engine이나 subtract_with_carry_engine 클래스도 매개변수를 많이 지정해야합니다. 그래서 표준에서는 몇 가지 엔진을 미리 정의해서 제공합니다. 그중 하나가 mt19937이라는 mersenne_twister_engine입니다. 이 엔진은 다음과 같이 정의되어 있습니다.

using mt19937 = mersenne_twister_engine<unsigned int, 32, 624, 397, 31, 0x9908b0df, 11, 0xffffffff, 7, 0x9d2c5680, 15,
    0xefc60000, 18, 1812433253>;

매개변수의 의미를 제대로 이해하려면 메르센 트위스터 알고리즘을 깊이 이해해야하며, 일반적으로 수학 전공자가 아니라면 이러한 매개변수값을 변경할 일은 없기 때문에 다룰 능력도 없을 뿐더러... 여기서 다루지는 않겠습니다.

따라서 mt19937처럼 C++에서 제공하는 타입 앨리어스를 사용하면 거의 대부분은 문제가 없을 것입니다.

Random Number Engine Adapters

난수 엔진 어댑터(random number engine adapter)는 난수 생성에 사용되는 엔진(베이스 엔진)의 결과를 수정할 때 사용하며, 어댑터 패턴(apdater pattern)의 대표적인 예입니다.

C++ 라이브러리에 정의된 어댑터는 3가지가 있습니다.

template<class Engine, size_t p, size_t r> class
    discard_block_engine {...}
template<class Engine, size_t w, class UIntT> class
    independent_bits_engine {...}
template<class Engine, size_t k> class
    shuffle_order_engine {...}

discard_block_engine 어댑터는 베이스 엔진에서 생성된 값 중에서 일부를 제거하는 방식으로 난수를 생성합니다. 이 어댑터는 3가지 매개변수를 받습니다. 첫 번째는 연결한 엔진에 대한 것이고, 두 번째는 블록 크기인 p이고, 세 번째는 사용된 블록 크기인 r입니다. 베이스 엔진은 p개의 난수를 생성하는 데 사용됩니다. 그러면 어댑터는 p-r개의 난수를 제거하고, 나머지 난수만 리턴합니다.

independent_bits_engine 어댑터는 w로 지정된 비트 수로부터 베이스 엔진이 생성한 여러가지 난수를 조합하는 방식으로 난수를 생성합니다.

shuffle_order_engine 어댑터는 베이스 엔진과 똑같은 난수를 생성하지만 리턴 순서는 다릅니다.

이러한 어댑터의 내부 동작 과정은 기반이 되는 수학적 기법에 따라 다르며, 여기서는 다룰 능력이 안되므로 패스합니다.. ㅠ

Predefined Engines and Engine Adapters

앞서 설명했듯이 난수 엔진과 엔진 어댑터의 매개변수는 건드리지 않는 것이 좋습니다. 그 대신 표준에서 정의해둔 엔진과 엔진 어댑터를 사용하는 것이 좋습니다. C++에는 다음과 같은 엔진과 엔진 어댑터를 기본으로 제공합니다. 모두 <random> 헤더 파일에 정의되어 있으며, 템플릿 인수가 복잡하게 지정되어 있습니다만, 이러한 인수들의 의미를 몰라도 엔진과 엔진 어댑터를 사용하는 데는 문제가 없을 것입니다.

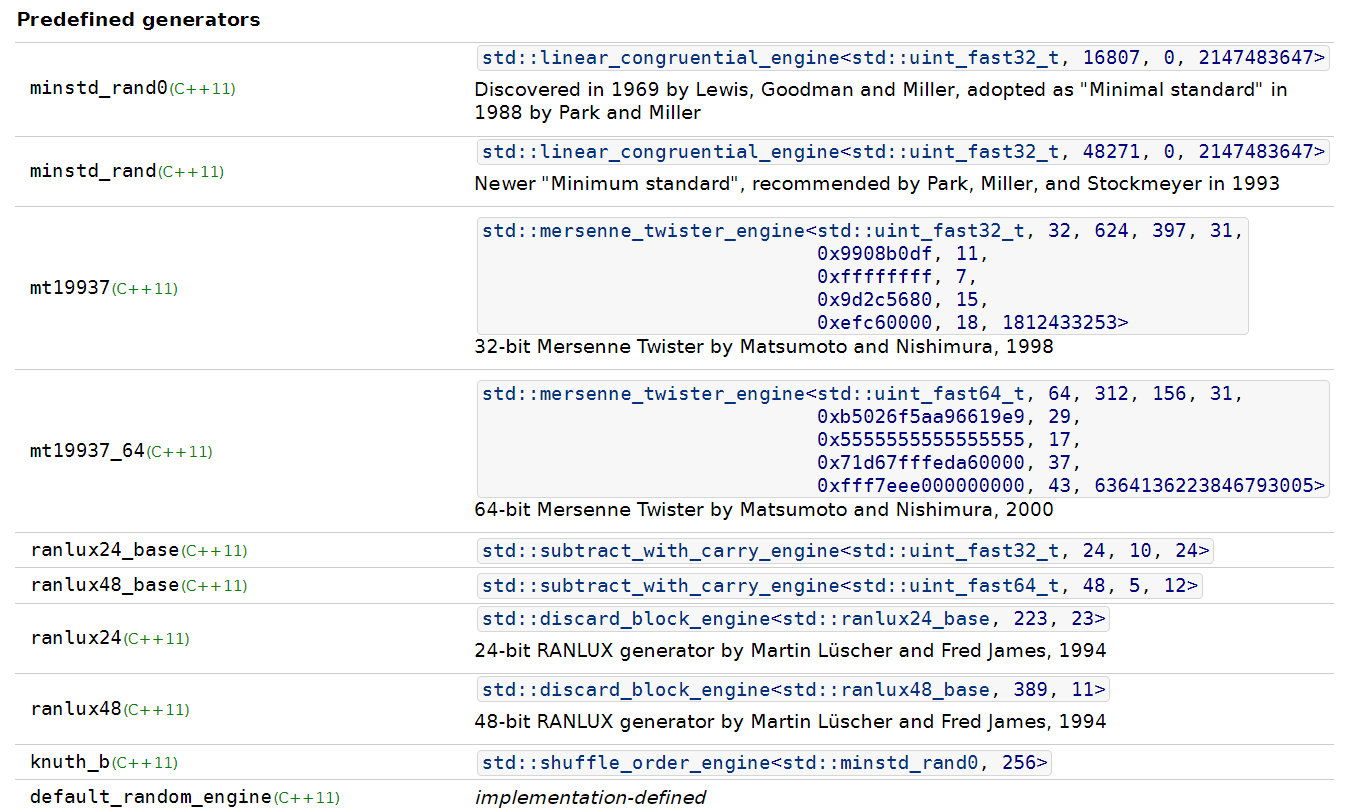
여기서 default_random_engine은 컴파일러마다 다르며 MSVC의 경우에는 mt19937을 사용하고 있습니다.

Generating Random Numbers

난수를 생성하기 전에는 먼저 엔진 인스턴스부터 생성해야 합니다. 소프트웨어 기반 엔진을 사용할 때는 분포도 지정해주어야 합니다. 여기서 분포는 주어진 범위 안에서 숫자가 분포되는 방식을 표현하는 수학 공식입니다. 추천하는 엔진 생성 방법은 위에서 소개한 기본 제공 엔진 중 하나를 그냥 하는 것입니다.

다음 코드는 기본 제공 엔진이자 소프트웨어 기반 난수 생성기인 mt19937이란 엔진을 사용합니다. 기존 rand() 생성기를 사용할 때와 마찬가지로 소프트웨어 기반 엔진도 시드로 초기화해야 합니다. srand() 에서는 주로 현재 시스템 시간을 시드로 사용했지만, 최신 C++에서는 random_device로 시드를 생성하거나 random_device를 사용하기 힘든 상황이라면 차선책으로 시스템 시간에 기반한 시드를 사용하는 것을 권장합니다.

std::random_device seeder;
const auto seed{ seeder.entropy() ? seeder() : time(nullptr) };
std::mt19937 engine{ static_cast<std::mt19937::result_type>(seed) };

다음으로 분포를 지정해보겠습니다. 이 예제코드에서는 1부터 99 사이의 범위에 대해 균등 정수 분포(uniform integer distribution)으로 지정합니다. 분포에 대한 자세한 사항은 아래에서 조금 더 자세히 소개하도록 하고, 일단 여기서는 다음과 같은 방식으로 균등 분포를 사용한다는 점만 알아두고 넘어가겠습니다.

std::uniform_int_distribution<int> distribution{ 1, 99 };

엔진과 분포를 정의했으면 이제 분포에 대한 함수 호출 연산자에 엔진을 인수로 지정해서 호출합니다. 그러면 난수가 생성됩니다.

std::cout << distribution(engine) << std::endl;

위 코드에서 볼 수 있듯이 소프트웨어 기반 엔진으로 난수를 생성하기 위해서는 항상 엔진과 분포를 지정해주어야 합니다. 하지만 <functional> 헤더에 정의된 std::bind() 유틸리티를 사용하면 엔진과 분포를 지정하지 않고도 난수를 생성할 수 있습니다.

다음 예제 코드는 위의 코드와 마찬가지로 mt19937 엔진과 균등 분포를 적용한 다음 std::bind()로 dist()의 첫 번째 매개변수를 eng로 바인딩해서 gen()을 정의합니다. 이렇게 하면 난수를 생성할 때마다 인수를 지정하지 않고 gen()만 호출하면 됩니다. 그런 다음 generate() 알고리즘과 gen()을 함께 조합하여 10개의 난수로 구성된 벡터를 생성합니다.

#include <iostream>
#include <random>
#include <functional>
#include <vector>
#include <algorithm>

int main()
{
    std::random_device seeder;
    const auto seed{ seeder.entropy() ? seeder() : time(nullptr) };
    std::mt19937 engine{ static_cast<std::mt19937::result_type>(seed) };
    std::uniform_int_distribution<int> distribution(1, 99);

    auto generator = std::bind(distribution, engine);

    std::vector<int> values(10);
    std::generate(values.begin(), values.end(), generator);

    for (auto i : values) { std::cout << i << " "; }
}

비록 gen()의 타입을 정확히 몰라도 gen()을 난수 생성기를 사용하려는 다른 함수에 인수로 전달할 수 있습니다. 이때 두가지 옵션이 있습니다. 하나는 std::function<int()> 타입으로 매개변수를 지정하는 것이고, 다른 하나는 함수 템플릿으로 지정하는 것입니다. 방금 예제를 다음 fillVector() 함수에서 난수를 생성하는 데 활용해도 됩니다. 이 코드는 std::function으로 구현했습니다.

void fillVector(std::vector<int>& values, const std::function<int()>& generator)
{
    std::generate(values.begin(), values.end(), generator);
}

함수 템플릿 버전은 다음과 같습니다.

template<typename T>
void fillVector(std::vector<int>& values, const T& generator)
{
    std::generate(values.begin(), values.end(), generator);
}

이렇게 작성한 함수는 다음과 같이 사용할 수 있습니다.

int main()
{
    std::random_device seeder;
    const auto seed{ seeder.entropy() ? seeder() : time(nullptr) };
    std::mt19937 engine{ static_cast<std::mt19937::result_type>(seed) };
    std::uniform_int_distribution<int> distribution(1, 99);

    auto generator = std::bind(distribution, engine);

    std::vector<int> values(10);
    fillVector(values, generator);

    for (auto i : values) { std::cout << i << " "; }
}

Random Number Distributions

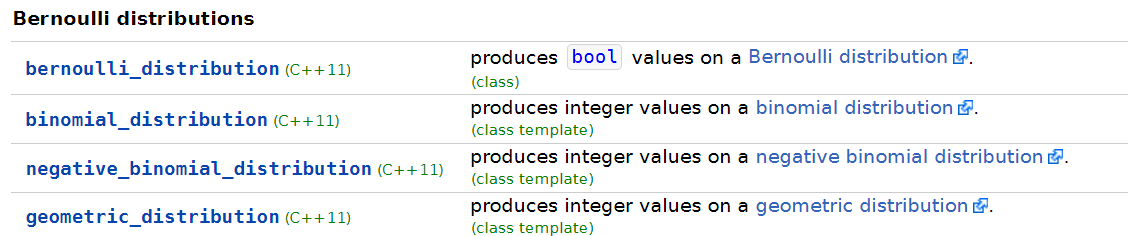
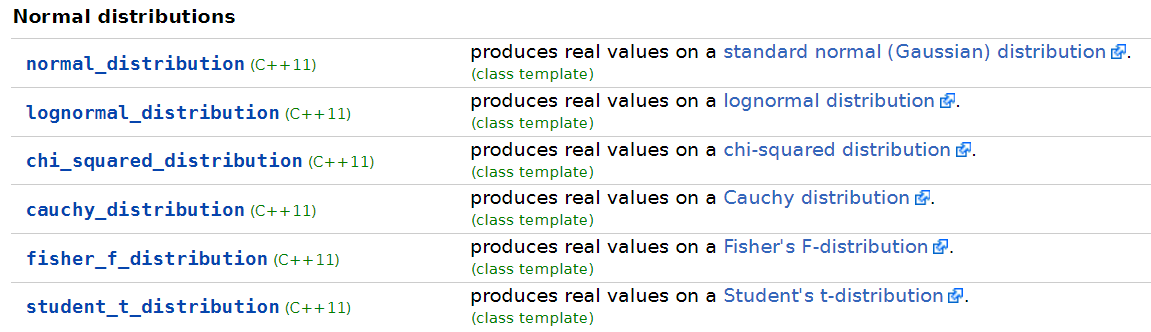
분포는 일정한 범위에서 숫자가 분포된 방식을 표현하는 수학 공식입니다. 난수 발생기 라이브러리는 의사 난수 엔진에서 사용할 수 있도록 다음과 같이 다양하게 정의된 분포를 함께 제공합니다.

- 균등 분포 (uniform distributions)

- 베르누이 분포 (bernoulli distributions)

- 푸아송 분포 (poisson distributions)

- 정규 분포 (normal distributions)

- 표본 분포 (sampling distribution)

각 분포마다 정의된 매개변수를 지정해주어야 하긴 합니다. 이러한 매개변수를 설명하려면 수학적 배경이 필요하고, 저도 잘 모르기 때문에 다르지는 않고, 책에서 설명하는 난수를 생성하는데 각 분포가 미치는 영향만 살펴보도록 하겠습니다.

각 분포의 특성은 그래프를 보면 가장 이해하기가 쉽습니다.

예를 들어 다음 코드는 1과 99사이에 백만 개의 난수를 생성하는데, 그중에서 특정한 숫자가 무작위로 선택한 횟수를 셉니다. 이렇게 센 결과를 map에 저장하는데, 키는 1과 99 사이의 수고 값은 해당 키가 무작위로 선택된 횟수입니다. 코드에서 루프를 수행한 후 나온 최종 결과를 CSV 파일에 저장합니다.

#include <iostream>
#include <fstream>
#include <random>
#include <functional>
#include <map>

int main()
{
    const unsigned int Start{ 1 };
    const unsigned int End{ 99 };
    const unsigned int Iterations{ 1'000'000 };

    std::random_device seeder;
    const auto seed{ seeder.entropy() ? seeder() : time(nullptr) };
    std::mt19937 engine{ static_cast<std::mt19937::result_type>(seed) };
    std::uniform_int_distribution<int> distribution(1, 99);

    auto generator = std::bind(distribution, engine);

    std::map<int, int> histogram;
    for (unsigned int i = 0; i < Iterations; i++) {
        int randomNumber{ generator() };
        ++(histogram[randomNumber]);
    }

    // Write to a CSV file
    std::ofstream of{ "res.csv" };
    for (unsigned int i = Start; i <= End; i++) {
        of << i << "," << histogram[i] << std::endl;
    }
}

이렇게 나온 결과로 그래프를 다음과 같이 만들 수 있습니다.

위 그래프는 균등 메르센 트위스터의 결과를 표현한 것입니다. 가로축은 무작위로 생성된 숫자의 범위를 나타냅니다. 그래프를 살펴보면 1과 99 사이에 있는 각 숫자마다 무작위로 선택된 횟수는 대략 10,000번으로 모든 수가 고르게 선택되었음을 알 수 있습니다.

이 예제 코드에서 이제 균등 분포가 아닌 정규 분포를 적용해서 난수를 생성하도록 수정해보겠습니다. 코드에서 분포를 생성하는 문장을 다음과 같이 변경해주고, 정규 분포는 정수가 아닌 double 타입을 사용하므로 generator()를 호출하는 부분도 변경해줍니다.

// ...
std::normal_distribution<double> distribution(50, 10);
// ...
    int randomNumber{ static_cast<int>(generator()) };
// ...

아래 그래프는 이렇게 생성한 정규 분포에 따라 난수를 생성한 결과를 보여줍니다.

이 그래프를 보면 생성된 난수는 대부분 주어진 범위의 가운데 부분에 있는 수라는 것을 알 수 있습니다. 이 예제에서는 50이 무작위로 선택된 횟수는 대략 40,000번 정도이며, 20과 80이 선택된 횟수는 대략 500번 정도입니다.

'프로그래밍 > C & C++' 카테고리의 다른 글

[C++] 템플릿(Template) 심화편 (2) (0)	2022.03.01
[C++] 템플릿(Template) 심화편 (1) (0)	2022.03.01
[C++] chrono 라이브러리 (Date, Time 유틸리티) (0)	2022.02.27
[C++] String Localization (0)	2022.02.27
[C++] 알고리즘 (Algorithms) (3) (0)	2022.02.26

별준

[C++] 난수(random number) - random 라이브러리

References

Contents

C-Style Random Number Generation

Random Number Engines

Random Number Engine Adapters

Predefined Engines and Engine Adapters

Generating Random Numbers

Random Number Distributions

'프로그래밍 > C & C++' 카테고리의 다른 글

댓글

티스토리툴바

[C++] 난수(random number) - random 라이브러리

References

Contents

C-Style Random Number Generation

Random Number Engines

Random Number Engine Adapters

Predefined Engines and Engine Adapters

Generating Random Numbers

Random Number Distributions

'프로그래밍 > C & C++' 카테고리의 다른 글

관련글

댓글

티스토리툴바