[C++] 알고리즘 (Algorithms) (3)

References

Professional C++
https://en.cppreference.com/w/

연산 알고리즘 (Operational Algorithms) : for_each, for_each_n
분할 알고리즘 (Partition Algorithms) : partition_copy, partition
정렬 알고리즘 (Sorting Algorithms) : sort, stable_sort, is_sorted, is_sorted_until, nth_element
이진 탐색 알고리즘 (Binary Search Algorithms) : binary_search, lower_bound, upper_bound, equal_range
집합 알고리즘 (Set Algorithms) : includes, set_union, set_intersection, set_difference, set_symmetric_difference, merge
최대/최소 알고리즘 (Minimum/Maximum Algorithms) : min, max, minmax, min_element, max_element, minmax_element, clamp
병렬 알고리즘 (Parallel Algorithms)
수치 처리 알고리즘 (Numerical Processing Algorithms)
- iota, gcd, lcm
- Reduce algorithms : reduce, inner_product, transform_reduce
- Scan algorithms : exclusive_scan, inclusive_scan, partial_sum, transform_exclusive_scan, transform_inclusive_scan

이전 포스팅에 이어서 계속해서 C++에서 제공하는 알고리즘들에 대해 알아보도록 하겠습니다.

3. Operational Algorithms

표준라이브러리에서 제공하는 연산 알고리즘은 for_each()와 for_each_n() 뿐입니다. for_each() 알고리즘은주어진 범위에 있는 원소마다 콜백을 실행시키고, for_each_n() 알고리즘은 주어진 범위에 있는 원소 중에서 첫 번째부터 n번째 원소까지 콜백을 실행합니다. 이때 컨테이너의 원소에 대해 처리할 작업은 간단히 함수 콜백이나 람다 표현식으로 정의합니다. 여기서는 단지 이러한 알고리즘이 있다는 것만 알아두면 될 것 같습니다. 대부분 범위 기반 for문을 사용하는 것이 코드를 작성하는 것도 쉽고 읽기도 쉽습니다.

3.1 for_each

#include <iostream>
#include <algorithm>
#include <map>

int main()
{
    std::map<int, int> myMap{ {4, 40}, {5,50}, {6, 60} };
    std::for_each(myMap.begin(), myMap.end(), [](const auto& p)
        { std::cout << p.first << "->" << p.second << std::endl; });
}

위 코드를 실행한 결과는 다음과 같습니다.

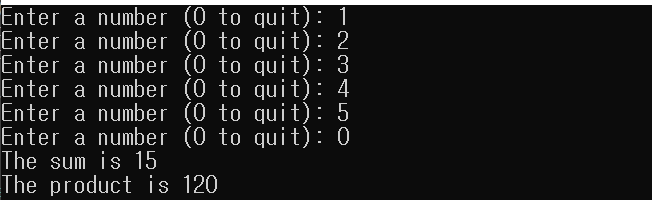
다음 예제는 주어진 범위의 원소의 합과 곱을 동시에 계산하기 위해 for_each() 알고리즘과 람다 표현식을 사용하는 방법을 보여줍니다. 여기서 사용하는 람다 표현식은 필요한 변수를 명시적으로 캡처합니다. 이때 레퍼런스로 캡처했는데, 그렇지 않으면 람다 표현식 안에서 변경한 sum과 product의 결과를 람다 표현식 밖에서 볼 수 없기 때문입니다.

int main()
{
    std::vector<int> myVector;
    populateContainer(myVector);

    int sum{ 0 };
    int product{ 1 };
    std::for_each(myVector.cbegin(), myVector.cend(),
        [&sum, &product](int i) {
            sum += i;
            product *= i;
        });
    std::cout << "The sum is " << sum << std::endl;
    std::cout << "The product is " << product << std::endl;
}

이 코드를 다음과 같이 functor로 구현해도 됩니다. 여기서는 for_each()로 각 원소에 대한 작업을 끝날 때마다 결과를 누적시키도록 구현했습니다. 예를 들어 합과 곱을 동시에 추적하도록 SumAndProduct 펑터를 작성하면 두 값을 한 번에 계산할 수 있습니다.

class SumAndProduct
{
public:
    void operator()(int value)
    {
        m_sum += value;
        m_product *= value;
    }
    int getSum() const { return m_sum; }
    int getProdcut() const { return m_product; }
private:
    int m_sum{ 0 };
    int m_product{ 1 };
};

int main()
{
    std::vector<int> myVector;
    populateContainer(myVector);

    SumAndProduct calculator;
    calculator = std::for_each(myVector.cbegin(), myVector.cend(), calculator);
    std::cout << "The sum is " << calculator.getSum() << std::endl;
    std::cout << "The product is " << calculator.getProdcut() << std::endl;
}

여기서 for_each()의 리턴값을 따로 저장하지 않고, 나중에 알고리즘이 끝난 후 calculator로부터 정보를 읽고 싶을 수도 있습니다. 하지만 이런 식으로는 처리할 수 없는데, for_each()는 이 functor를 복사하고 알고리즘이 끝난 다음에 이 복사본이 리턴되기 때문입니다. 따라서 제대로 동작하려면 반드시 리턴값을 캡처해야 합니다.

for_each()의 마지막 포인트는 콜백을 레퍼런스로 받도록 하여 그 내용을 수정할 수 있도록 만들 수 있습니다. 그러면 이터레이터 범위에서 값을 변경할수 있습니다.

int main()
{
    std::vector values{ 11,22, 33,44 };
    // Double each element in the values vector
    std::for_each(values.begin(), values.end(), [](auto& value) { value *= 2; });
    // Print all the elements of the values vector
    std::for_each(values.cbegin(), values.cend(),
        [](const auto& value) { std::cout << value << std::endl; });
}

3.2 for_each_n

for_each_n() 알고리즘은 주어진 범위의 begin 이터레이터, 반복할 원소 수, 함수 콜백을 인수로 받아서 '시작 지점 + n' 위치를 가리키는 이터레이터를 리턴합니다. 이 알고리즘도 경계값 검사를 수행하지 않습니다.

예를 들어 map의 첫 번째와 두 번째 원소에 대해서만 반복하려면 다음과 같이 작성합니다.

int main()
{
    std::map<int, int> myMap{ {4,40},{5,50}, {6,60} };
    std::for_each_n(myMap.cbegin(), 2, [](const auto& p)
        { std::cout << p.first << "->" << p.second << std::endl; });
}

4. Partition Algorithms

partition_copy()는 원본에 있는 원소를 복사하여서로 다른 두 대상으로 분할합니다. 이때 둘 중 어느 대상에 원소에 보낼지는 predicate의 실행 결과가 true냐 false냐에 따라 달라집니다. partition_copy()는 이터레이터 쌍을 리턴하는데, 그중 하나는 첫 번째 대상 범위에서 마지막으로 복사한 원소의 다음 지점을 가리키는 이터레이터이고, 다른 하나는 두 번째 대상 범위에서 마지막으로 복사한 원소의 다음 지점을 가리키는 이터레이터입니다. 이렇게 리턴된 이터레이터를 erase()와 함께 사용해서 두 대상 범위에서 초과된 원소를 삭제하도록 만들 수 있습니다. 구체적인 방법은 위에서 본 copy_if()와 같습니다.

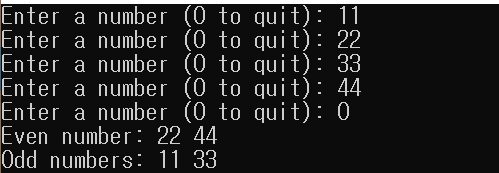
다음 코드는 사용자로부터 정수의 개수를 입력받아서 대상 범위를 짝수에 대한 vector와 홀수에 대한 vector로 분할합니다.

int main()
{
    std::vector<int> vec1, vecOdd, vecEven;
    populateContainer(vec1);
    vecOdd.resize(vec1.size());
    vecEven.resize(vec1.size());

    auto pairIter{ std::partition_copy(vec1.cbegin(), vec1.cend(),
        vecEven.begin(), vecOdd.begin(),
        [](int i) { return i % 2 == 0; }) };

    vecEven.erase(pairIter.first, vecEven.end());
    vecOdd.erase(pairIter.second, vecOdd.end());

    std::cout << "Even number: ";
    for (const auto& i : vecEven) { std::cout << i << " "; }
    std::cout << "\nOdd numbers: ";
    for (const auto& i : vecOdd) { std::cout << i << " "; }
}

위 코드를 실행한 결과는 다음과 같습니다.

partition() 알고리즘은 predicate에서 true를 리턴하는 원소가 false를 리턴하는 원소보다 앞에 나오도록 정렬합니다. 이때 두 개로 분할된 범위 내에서는 원래 순서가 유지되지 않습니다.

다음 코드는 vector에 있는 원소 중 짝수를 모두 홀수 앞에 나오도록 분할하는 예를 보여줍니다.

int main()
{
    std::vector<int> vec;
    populateContainer(vec);
    std::partition(vec.begin(), vec.end(), [](int i) { return i % 2 == 0; });

    std::cout << "Partitioned result: ";
    for (const auto& i : vec) { std::cout << i << " "; }
}

실행 결과는 다음과 같습니다.

그 밖에 is_partitioned(), stable_partition(), partition_point()가 있습니다. 자세한 설명은 생략하도록 하겠습니다.

5. Sorting Algorithms

표준 라이브러리에는 여러 가지 종류의 정렬 알고리즘을 제공합니다. 정렬 알고리즘은 컨테이너에 담긴 원소를 특정한 조건을 기준으로 순서에 맞게 유지하도록 재배치합니다. 그래서 순차 컨테이너에만 정렬 알고리즘을 적용할 수 있습니다. 항상 원소를 정렬된 상태로 유지하는 정렬 연관(ordered associative) 컨테이너에는 적용할 수 없습니다. 비정렬 연관(unordered associative) 컨테이너에도 적용할 수 없는데, 원래부터 정렬을 하지 않기 때문입니다. list나 forward_list와 같은 일부 컨테이너는 자체적으로 정렬 메소드를 제공합니다. 그래서 제너릭 정렬 알고리즘보다 자체 메소드로 구현하는 것이 훨씬 효율적입니다. 제너릭 정렬 알고리즘은 주로 vector, deque, array, C 스타일 배열에 적합합니다.

sort() 알고리즘은 주어진 범위에 있는 원소를 O(NlogN) 시간에 정렬합니다. sort()는 기본적으로 operator<를 이용해서 주어진 범위를 오름차순으로(낮은 것부터 높은 순) 정렬합니다. 순서를 바꾸고 싶다면 greater와 같은 다른 비교자를 지정하면 됩니다.

sort()를 변형한 stable_sort()란 알고리즘도 있습니다. 이 알고리즘은 주어진 범위에서 같은 원소에 대해서는 원본에 나온 순서를 그대로 유지합니다. 따라서 sort() 알고리즘보다 성능이 조금 떨어집니다.

sort()를 사용하는 예는 다음과 같습니다.

int main()
{
    std::vector<int> values;
    populateContainer(values);

    std::sort(values.begin(), values.end(), std::greater<>{});
}

또한 표준 라이브러리에는 is_sorted(), is_sorted_until()도 제공합니다. is_sorted()는 주어진 범위가 정렬된 상태라면 true를 리턴하며, is_sorted_until()은 이터레이터를 리턴하는데 이 이터레이터 앞에 나온 원소까지는 모두 정렬된 상태입니다.

nth_element()는 소위 selective algorithm이라고 불리며, 매우 강력한 알고리즘입니다.

주어진 원소의 범위와 이 범위에서 n번째 원소의 이터레이터를 가지고, 알고리즘은 n번째 위치까지 정렬하고 n번째 다음으로 나오는 원소들은 정렬된 후 n번째 위치하는 원소보다 크거나 같습니다. 여기서 흥미로운 점은 이 알고리즘은 O(n)의 선형 시간 내에 수행됩니다. 따라서, 전체 범위에 대해 정렬하는 것이 아닌 n번째 까지만 정렬할 필요가 있을 때 이 알고리즘을 사용하면 sort()(O(NlogN))보다 빠르게 정렬하여 원하는 결과를 얻을 수 있습니다.

다음 예제 코드는 vector에 16개의 원소를 넣고 섞은 다음에 5번째 위치까지 정렬하는 코드입니다.

int main()
{
    std::vector<int> values;
    std::random_device seeder;  // defined in <random> header file
    const auto seed{ seeder.entropy() ? seeder() : time(nullptr) };
    std::default_random_engine engine{
        static_cast<std::default_random_engine::result_type>(seed) };

    for (int i = 0; i < 16; i++)
        values.push_back(i);
    std::shuffle(values.begin(), values.end(), engine);

    std::nth_element(values.begin(), values.begin() + 5, values.end());
    for (const auto& i : values) { std::cout << i << " "; }
}

결과는 다음과 같습니다.

이번에는 vector의 원소 개수를 32보다 크게 설정하여 동일한 코드를 실행시킨 결과입니다 (33개로 설정).

이번에는 뒤쪽의 원소들은 제대로 정렬되지 않았지만, 5번째 원소보다는 모두 크다는 것을 알 수 있습니다.

이처럼 nth_element()는 n번째 원소까지 정렬되는 것을 보장하며, n번째 원소 다음의 원소들은 n번째 위치하는 원소보다 크거나 같다라는 것을 보장하면 n번째 다음의 원소들이 정렬되는 것은 보장하지 않습니다.

vector의 크기가 16일 때, 모든 원소들이 정렬된 것은 nth_element의 내부 구현에 따른 것입니다. 이 알고리즘 내부에서는 주어진 범위의 크기가 32보다 클 때 분할 정복 알고리즘을 사용하여 정렬하고, 32 이하일 때는 insertion 알고리즘을 사용하도록 되어 있습니다.

/* <algorithm> 내용 중 일부 */
// COMMON SORT PARAMETERS
_INLINE_VAR constexpr int _ISORT_MAX = 32; // maximum size for insertion sort

6. Binary Search Algorithms

탐색 알고리즘 중에는 정렬된 시퀀스에 대해서만 적용하거나, 검색 대상 기준으로 분할된 시퀀스에 대해서만 적용하는 이진 탐색 알고리즘이 있습니다. 이러한 알고리즘에는 binary_search(), lower_bound(), upper_bound(), equal_range()가 있습니다. lower_bound(), upper_bound(), equal_range() 알고리즘은 map과 set 컨테이너에서 제공하는 동일한 이름의 메소드와 비슷합니다.

lower_bound() 알고리즘은 정렬된 알고리즘에서 주어진 값보다 작지 않은(크거나 같은) 원소 중에서 첫 번째 원소를 찾습니다. 이 알고리즘은 주로 정렬된 vector에 새 값을 추가해도 계속 정렬된 상태를 유지할 수 있는 적절할 추가 지점을 찾을 때 사용합니다.

예를 들면 다음과 같습니다.

int main()
{
    std::vector<int> values;
    populateContainer(values);

    std::sort(values.begin(), values.end());

    std::cout << "Sorted vector: ";
    for (const auto& i : values) { std::cout << i << " "; }
    std::cout << "\n";

    while (true) {
        int number;
        std::cout << "Enter a number to insert (0 to quit): ";
        std::cin >> number;
        if (number == 0) { break; }

        auto iter{ std::lower_bound(values.begin(), values.end(), number) };
        values.insert(iter, number);

        std::cout << "New vector: ";
        for (const auto& i : values) { std::cout << i << " "; }
        std::cout << "\n";
    }
}

binary_search() 알고리즘은 선형 시간보다 빠른 로그 시간에 원소를 검색합니다. 이 알고리즘은 탐색할 범위를 지정하는 begin, end 이터레이터와 탐색할 값, 그리고 옵션으로 비교 콜백을 인수로 받습니다. 주어진 범위에서 값을 찾으면 true를 리턴하고, 그렇지 않으면 false를 리턴합니다.

binary_search()의 사용법은 다음과 같습니다.

int main()
{
    std::vector<int> values;
    populateContainer(values);

    std::sort(values.begin(), values.end());

    std::cout << "Sorted vector: ";
    for (const auto& i : values) { std::cout << i << " "; }
    std::cout << "\n";

    while (true) {
        int number;
        std::cout << "Enter a number to insert (0 to quit): ";
        std::cin >> number;
        if (number == 0) { break; }

        if (std::binary_search(values.cbegin(), values.cend(), number)) {
            std::cout << "That number is in the vector.\n";
        }
        else {
            std::cout << "That number is not in the vector.\n";
        }
    }
}

7. Set Algorithms

집합 알고리즘은 정렬된 범위라면 어떤 것에도 적용할 수 있습니다. includes() 알고리즘은 부분집합을 판별하는데, 인수로 주어진 두 정렬된 범위 중에서 한쪽의 원소가 다른 쪽 원소에 모두 포함되는지 검사합니다. 포함 관계를 판단할 때는 순서를 고려하지 않습니다.

set_union(), set_intersection(), set_difference(), set_symmetric_difference() 알고리즘은 각각 수학의 집합에서 말하는 합집합(union), 교집합(intersection), 차집합(difference), 대칭차집합(symmectric difference)을 구현한 것입니다. 이에 대한 자세한 내용은 생략하고, 집합 알고리즘을 사용하는 예제 코드를 살펴보겠습니다.

template<typename Iterator>
void DumpRange(std::string_view message, Iterator begin, Iterator end)
{
    std::cout << message;
    std::for_each(begin, end, [](const auto& element) { std::cout << element << " "; });
    std::cout << std::endl;
}

int main()
{
    std::vector<int> vec1, vec2, result;
    std::cout << "Enter elements for set 1:\n";
    populateContainer(vec1);
    std::cout << "Enter elements for set 2:\n";
    populateContainer(vec2);

    std::sort(vec1.begin(), vec1.end());
    std::sort(vec2.begin(), vec2.end());

    DumpRange("Set 1: ", vec1.cbegin(), vec1.cend());
    DumpRange("Set 2: ", vec2.cbegin(), vec2.cend());

    if (std::includes(vec1.cbegin(), vec1.cend(), vec2.cbegin(), vec2.cend())) {
        std::cout << "The second set is a subset of the first.\n";
    }
    if (std::includes(vec2.cbegin(), vec2.cend(), vec1.cbegin(), vec1.cend())) {
        std::cout << "The first set is a subset of the second.\n";
    }

    result.resize(vec1.size() + vec2.size());
    auto newEnd{ std::set_union(vec1.cbegin(), vec1.cend(), vec2.cbegin(), vec2.cend(), result.begin()) };
    DumpRange("The union is: ", result.begin(), newEnd);

    newEnd = std::set_intersection(vec1.cbegin(), vec1.cend(), vec2.cbegin(), vec2.cend(), result.begin());
    DumpRange("The intersection is: ", result.begin(), newEnd);

    newEnd = std::set_difference(vec1.cbegin(), vec1.cend(), vec2.cbegin(), vec2.cend(), result.begin());
    DumpRange("The difference between set 1 and 2 is: ", result.begin(), newEnd);

    newEnd = std::set_symmetric_difference(vec1.cbegin(), vec1.cend(), vec2.cbegin(), vec2.cend(), result.begin());
    DumpRange("The symmetric difference is: ", result.begin(), newEnd);
}

위 코드를 실행한 결과는 다음과 같습니다.

merge() 알고리즘을 사용하면 정렬된 두 범위를 하나로 합칠 수 있습니다. 이때 정렬 순서는 그대로 유지됩니다. 그 결과두 범위에 있던 원소를 모두 담은 정렬된 범위가 리턴되며, 이는 선형 시간에 처리됩니다. 이 알고리즘의 파라미터는 다음과 같습니다.

첫 번째 source 범위에 대한 begin, end 이터레이터
두 번째 source 범위에 대한 begin, end 이터레이터
destination 범위에 대한 begin 이터레이터
비교 연산을 수행하는 콜백(option)

두 범위를 하나로 합친 결과를 sort()로 정렬해도 merge()와 똑같은 효과를 낼 수 있지만 성능이 O(NlogN)이므로 선형 복잡도를 갖는 merge()에 비해 성능이 떨어집니다.

merge()를 사용하는 예제는 다음과 같습니다.

int main()
{
    std::vector<int> vectorOne, vectorTwo, vectorMerged;
    std::cout << "Enter values for first vector:\n";
    populateContainer(vectorOne);
    std::cout << "Enter values for second vector:\n";
    populateContainer(vectorTwo);

    // Sort both containers
    sort(vectorOne.begin(), vectorOne.end());
    sort(vectorTwo.begin(), vectorTwo.end());

    // Make sure enough size
    vectorMerged.resize(vectorOne.size() + vectorTwo.size());

    std::merge(vectorOne.cbegin(), vectorOne.cend(),
        vectorTwo.cbegin(), vectorTwo.cend(), vectorMerged.begin());

    DumpRange("Merged vector: ", vectorMerged.cbegin(), vectorMerged.cend());
}

8. Minimum/Maximum Algorithms

min()과 max() 알고리즘은 모든 타입의 원소를 operator< 또는 사용자가 정의한 binary predicate로 비교해서 각각 최소 원소와 최대 원소에 대한 const 레퍼런스를 리턴합니다. minmax() 알고리즘은 두 개 이상 원소 중에서 최솟값과 최댓값을 pair로 리턴합니다. 이러한 알고리즘은 이터레이터를 매개변수로 받지 않습니다.

반면 min_element()와 max_element(), minmax_element()는 이터레이터로 지정한 범위에 대해 주어진 작업을 처리합니다.

예제 코드는 다음과 같습니다.

int main()
{
    int x{ 4 }, y{ 5 };
    std::cout << "x is "<< x << " and y is " << y << std::endl;
    std::cout << "Max is " << std::max(x, y) << std::endl;
    std::cout << "Min is " << std::min(x, y) << std::endl;
    // Using max() and min() on more than two values.
    int x1{ 2 }, x2{ 9 }, x3{ 3 }, x4{ 12 };
    std::cout << "Max of 4 elements is " << std::max({ x1, x2, x3, x4 }) << std::endl;
    std::cout << "Min of 4 elements is " << std::min({ x1, x2, x3, x4 }) << std::endl;
    // Using minmax().
    auto p2{ std::minmax({ x1, x2, x3, x4 }) }; // p2 is of type pair<int, int>.
    std::cout << "Minmax of 4 elements is <" << p2.first << "," << p2.second << ">" << std::endl;
    // Using minmax() + C++17 structured bindings.
    auto [min1, max1] { std::minmax({ x1, x2, x3, x4 }) };
    std::cout << "Minmax of 4 elements is <" << min1 << "," << max1 << ">" << std::endl;
    // Using minmax_element() + C++17 structured bindings.
    std::vector values{ 11, 33, 22 };
    auto [min2, max2] { std::minmax_element(values.cbegin(), values.cend()) };
    std::cout << "minmax_element() result: <" << *min2 << "," << *max2 << ">" << std::endl;
}

실행 결과는 다음과 같습니다.

std::clamp()는 <algorithm>에 정의된 간단한 헬퍼 함수입니다. 주어진 값(v)이 최솟값(lo)과 최댓값(hi) 사이에 있는지 검사합니다. v < lo라면 lo에 대한 레퍼런스를 리턴하고, v > hi라면 hi에 대한 레퍼런스를 리턴합니다. 나머지 경우는 v에 대한 레퍼런스를 리턴합니다.

예를 들면 다음과 같습니다.

int main()
{
    std::cout << std::clamp(-3, 1, 10) << std::endl;
    std::cout << std::clamp(3, 1, 10) << std::endl;
    std::cout << std::clamp(22, 1, 10) << std::endl;
}

9. Parallel Algorithms

C++17부터 성능 향상을 위한 병렬 처리 알고리즘이 표준 라이브러리에 60개 이상 추가되었습니다. 대표적인 예로 for_each(), all_of(), copy(), count_if(), find(), replace(), search(), sort(), transform() 등이 있습니다.

병렬 실행을 지원하는 알고리즘은 소위 execution policy(실행 정책)이라 부르는 옵션을 첫 번째 매개변수로 받습니다.

이러한 실행 정책을 이용해서 주어진 알고리즘을 병렬로 실행할 지, 아니면 벡터 방식으로 순차적으로 처리할 지 결정합니다. 컴파일러가 코드를 벡터화할 때, 컴파일러는 몇몇 CPU 명령(instruction)을 하나의 vector CPU 명령으로 교체합니다. vector instruction은 다중 데이터에 대한 몇몇 연산을 하나의 하드웨어 instruction으로 수행합니다. 이러한 작업은 single instruction multiple data(SIMD) 명령이라고 알려져 있습니다. 여기에는 4가지 실행 정책 타입이 있고, 모두 <execution> 헤더 파일에 std::execution 네임 스페이스 아래에 있습니다.

EXECUTION POLICY TYPE	GLOBAL INSTANCE	DESCRIPTION
sequenced_policy	seq	알고리즘을 순차적으로 실행
parallel_policy	par	알고리즘을 여러 스레드를 이용해 병렬로 실행
parallel_unsequenced_policy	par_unseq	여러 스레드를 이용해 알고리즘 실행을 병렬화하고, 또한 벡터화함
unsequenced_policy (C++20)	unseq	알고리즘 실행을 벡터화하지만, 병렬화하지는 않음

표준 라이브러리의 구현마다 실행 정책을 얼마든지 추가할 수는 있습니다.

이 실행 정책을 알고리즘에 적용하는 방법은 다음과 같습니다. 여기서는 vector의 원소들을 실행 정책을 이용해 정렬합니다.

std::sort(std::execution::par, myVector.begin(), myVector.end());

여기서 parallel_unsequenced_policy 또는 unsequenced_policy로 알고리즘을 실행하는 경우에 대해 좀 더 살펴 볼 필요가 있습니다. 이 실행 정책에서 콜백을 호출하는 함수 호출은 순차적이지 않고 서로 교차(interleaved)해서 실행될 수 있습니다. 이는 컴파일러가 코드를 벡터화하도록 해줍니다. 그러나 이는 또한 함수 콜백에서 할 수 있는 일에 제약사항이 많다는 것을 의미합니다. 예를 들어 메모리를 할당하거나 해제할 수 없고, 뮤텍스를 획득할 수 없으며 잠금에 제약이 없는 std::atomic을 사용할 수 없습니다. 나머지 실행 정책들은 함수 호출을 순차적으로 실행할 수는 있지만 정확한 순서는 보장할 수 없습니다. 이러한 정책은 함수 콜백에서 할 수 있는 일에 대해 제약사항을 두지 않습니다.

병렬 알고리즘은 데이터 경쟁(race condition)이나 데드락(deadlock)에 대한 대비책을 제공하지 않기 때문에 알고리즘을 병렬로 실행할 때 이러한 상황에 직접 대처해야 합니다. 이에 관한 내용은 여기서 다루지는 않겠습니다.

비록 병렬 실행이 아닌 버전에서는 constexpr이더라도, 병렬 버전의 동일한 알고리즘은 constexpr이 아닙니다.

병렬 버전의 몇몇 알고리즘의 리턴 타입은 병럴이 아닌 버전과 비교해서 약간 다를 수 있습니다. 예를 들어 병렬 실행이 아닌 for_each()는 제공된 콜백을 리턴하지만, 병렬 버전의 for_each()는 아무것도 리턴하지 않습니다.

10. Numerical Processing Algorithms

수치 처리 알고리즘 중에서 accumulate()는 알고리즘에 대한 첫 번째 포스팅에서 살펴봤었습니다. 이번에는 그 밖에 다른 수치 알고리즘 중에서 몇 가지 예제들을 살펴보겠습니다.

10.1 iota

iota() 알고리즘도 <numeric> 헤더 파일에 정의되어 있으며, 주어진 범위에서 주어진 값으로 시작해서 operator++로 값을 순차적으로 생성하는 방식으로 값에 대한 시퀀스를 만듭니다.

다음 코드는 이 알고리즘을 정수 타입 원소에 대한 vector에 적용하는 예를 보여줍니다. 참고로 정수가 아닌 다른 타입에서도 operator++만 구현되어 있으면 얼마든지 적용할 수 있습니다.

int main()
{
    std::vector<int> vec(10);
    std::iota(vec.begin(), vec.end(), 5);
    for (auto& i : vec) { std::cout << i << " "; }
}

10.2 gcd / lcm

gcd() 알고리즘은 인수로 지정한 두 정수에 대해 최대공약수(greates common divisor)를 리턴하고, lcm() 알고리즘은 최소공배수(least common multiple)을 리턴합니다.

예를 들면 다음과 같습니다.

int main()
{
    auto g{ std::gcd(3, 18) }; // g = 3
    auto l{ std::lcm(3, 18) }; // l = 18
}

10.3 Reduce Algorithms

표준 라이브러리에는 다음의 4가지 reduce 알고리즘을 제공합니다 : accumulate(), reduce(), inner_product(), transform_reduce(). 모든 reduce 알고리즘은 주어진 범위에서 두 원소를 결합하면서 마지막 하나의 원소가 남을 때까지 연산을 반복적으로 수행합니다. 이 알고리즘들은 avccumulate, aggregate, compress, inject, 또는 fold 알고리즘이라고도 불립니다.

10.3.1 reduce

std::accumulate()는 표준 라이브러리 알고리즘 중에서 병렬 실행을 지원하지 않는 몇 안되는 것 중에 하나입니다. 대신 C++17에서 추가된 std::reduce() 알고리즘에 병렬 실행 옵션을 지정해서 주어진 값의 합을 구할 수 있습니다.

예를 들어 다음의 코드들은 모두 벡터의 합을 구하지만, reduce()는 병렬화 및 벡터화 버전으로 동작하여 앞서 나온 것보다 실행 속도가 훨씬 빠릅니다. 성능 향상의 차이는 입력의 범위가 클수록 두드러집니다.

int main()
{
    std::vector values{ 1,3,6,4,6,9 };
    double result1{ std::accumulate(values.cbegin(), values.cend(), 0.0) };
    double result2{ std::reduce(std::execution::par_unseq, values.cbegin(), values.cend()) };
}

일반적으로 accumulate()와 reduce()는 초기값은 Init이고 이항 연산이 \(\Theta\)일 때, 다음과 같이 [\(x_0, x_n\)) 범위의 원소들을 모두 더합니다.

\[\text{Init }\Theta x_0 \Theta x_1 \Theta \cdots \Theta x_{n-1}\]

기본적으로 accumulate()의 이항 연산자는 operator+이며, reduce()는 std::plus 입니다.

10.3.2 inner_product

inner_product()는 두 시퀀스(벡터)의 내적(inner product)를 구합니다. 예를 들어 다음 코드는 (1*9)+(2*8)+(3*7)+(4*6)을 계산합니다.

int main()
{
    std::vector v1{ 1,2,3,4 };
    std::vector v2{ 9,8,7,6 };
    std::cout << std::inner_product(v1.cbegin(), v1.cend(), v2.cbegin(), 0) << std::endl;
}

위 코드를 실행하면 70이 출력됩니다.

10.3.3 transform_reduce

inner_product 역시 병렬 실행을 지원하지 않습니다. 이 알고리즘 대신 transform_reduce()를 사용하면 옵션으로 병렬 실행을 지정해서 내적을 계산할 수 있습니다. 사용 방법은 reduce()와 같으며 여기서 예제는 생략하도록 하겠습니다.

transform_reduce()는 초기값이 Init이고, 단항 함수 \(f\)와 이항 연산자 \(\Theta\)가 주어졌을 때 다음 수식에 따라 [\(x_0, x_n\)) 범위에 있는 원소의 합을 구합니다.

\[\text{Init }\Theta f(x_0) \Theta f(x_1) \Theta \cdots \Theta f(x_{n-1})\]

10.4 Scan Algorithms

스캔 알고리즘은 prefix sum, cummulative sum, 또는 partial sum 알고리즘으로 불립니다.

스캔 알고리즘에는 exclusive_scan(), inclusive_scan() / partial_sum(), transform_exclusive_scan(), transform_inclusive_scan() 이 있으며 모두 <numeric>에 정의되어 있습니다.

다음의 표는 [\(x_0, x_n\)) 범위에 있는 원소에 대해 초깃값으로 Init(partial_sum()의 경우에는 0)을 지정하고, 연산자로 \(\Theta\)를 지정했을 때 [\(y_0, y_n\)) 범위에 있는 원소의 합을 exclusive_scan()으로 구하는 과정과 inclusive_scan() / partial_sum()으로 구하는 과정을 보여주고 있습니다.

transform_exclusive_scan()과 transform_inclusive_scan()은 모두 합을 구하기 전에 원소에 단항 함수를 적용합니다. 이는 transform_reduce()가 reduce 연산을 적용하기 전에 원소마다 단항 함수를 적용하는 것과 비슷합니다.

여기서 스캔 함수들에는 모두 병렬 실행 옵션이 적용됩니다. 각 알고리즘의 평가 순서는 정확히 알 수 없습니다(비결정적 non-deterministic). 반면 partial_sum()과 accumulate()는 왼쪽부터 오른쪽 순으로 평가됩니다. 바로 이런 이유 때문에 partial_sum과 accumulate를 병렬로 실행할 수 없습니다.

'프로그래밍 > C & C++' 카테고리의 다른 글

[C++] chrono 라이브러리 (Date, Time 유틸리티) (0)	2022.02.27
[C++] String Localization (0)	2022.02.27
[C++] 알고리즘 (Algorithms) (2) (0)	2022.02.26
[C++] 알고리즘 (Algorithms) (1) (0)	2022.02.26
[C++] 템플릿 (Templates) (0)	2022.02.24

별준

[C++] 알고리즘 (Algorithms) (3)

References

Contents

3. Operational Algorithms

3.1 for_each

3.2 for_each_n

4. Partition Algorithms

5. Sorting Algorithms

6. Binary Search Algorithms

7. Set Algorithms

8. Minimum/Maximum Algorithms

9. Parallel Algorithms

10. Numerical Processing Algorithms

10.1 iota

10.2 gcd / lcm

10.3 Reduce Algorithms

10.3.1 reduce

10.3.2 inner_product

10.3.3 transform_reduce

10.4 Scan Algorithms

'프로그래밍 > C & C++' 카테고리의 다른 글

댓글

티스토리툴바

[C++] 알고리즘 (Algorithms) (3)

References

Contents

3. Operational Algorithms

3.1 for_each

3.2 for_each_n

4. Partition Algorithms

5. Sorting Algorithms

6. Binary Search Algorithms

7. Set Algorithms

8. Minimum/Maximum Algorithms

9. Parallel Algorithms

10. Numerical Processing Algorithms

10.1 iota

10.2 gcd / lcm

10.3 Reduce Algorithms

10.3.1 reduce

10.3.2 inner_product

10.3.3 transform_reduce

10.4 Scan Algorithms

'프로그래밍 > C & C++' 카테고리의 다른 글

관련글

댓글

티스토리툴바